雙軸音圈電機快速反射鏡的系統建模與滑模控制

李智斌，李 亮，張建強，孫崇尚

（山東科技大學 電氣與自動化工程學院，山東 青島 266590）

1 引言

快速反射鏡（Fast Steering Mirror，FSM）作為一種精密光束指向控制儀器，在激光通信、自適應光學、光束跟蹤等高精密光學系統中扮演著重要角色，其伺服控制精度決定了高精密光學系統伺服精度的上限。基于音圈電機（Voice Coil Actuator，VCA）驅動的FSM 憑借其精度高、響應速度快、行程大和結構緊湊等優點在FSM 中占有主導地位［1］。

相比于壓電陶瓷驅動的FSM，VCA-FSM 沒有非線性遲滯和蠕變等不利特性，對環境適應性強，適用于空間、海洋等復雜環境下的系統控制。但是，VCA-FSM 普遍采用柔性支撐結構，對機械加工和裝調精度要求極高。然而，由于結構件加工誤差、裝配誤差和柔性支撐結構自身形變等因素，導致VCA-FSM 存在復雜軸間耦合問題［2］，嚴重影響系統的控制性能，以PID、頻域校正為代表的傳統控制方法難以解決復雜耦合系統的高性能控制問題。

目前，VCA-FSM 的控制系統設計以單軸控制策略為主，即不考慮軸間耦合，將實際系統視作是兩個單輸入單輸出系統，分別進行控制器的設計。其中，單軸控制策略又以PID 及其改進控制算法為主，如模擬PID 控制［3］、模糊自適應PID控制［4］、PID 自適應前饋復合控制［5］等，也有一些先進控制方法，如自適應控制［6］、自抗擾控制［7］、H∞混合靈敏度控制［8］等。上述控制方法都通過實驗驗證了其有效性，但忽略了系統必然存在的耦合特性，在存在強耦合特性的VCA-FSM 中難以取得較好的控制性能。

為實現對存在強耦合特性VCA-FSM 的高性能控制，需針對耦合模型設計雙軸控制方法。文獻［9］通過設計X軸校正控制器、Y軸校正控制器、X軸對Y軸的補償控制器以及Y軸對X軸的補償控制器，顯著提高了雙軸VCA-FSM 的穩定性和抗干擾能力。文獻［10］通過雙前饋與雙神經網絡的解耦算法分別補償直流耦合分量和非直流耦合分量，大幅度降低了X軸和Y軸間的耦合度。文獻［11］通過在控制回路中引入解算網絡，使X軸和Y軸相互獨立、互不影響，降低控制系統的設計難度，并在此基礎上實現了VCAFSM 的雙軸閉環控制。上述控制方法能夠有效降低系統的軸間耦合，提高控制精度，具有重要的理論意義和實際工程價值。但是，高精密光學系統不僅要求VCA-FSM 具有較高指向精度，同時要求其具有高跟蹤帶寬，且能夠有效校正載體抖動和大氣擾動等因素帶來的干擾。而上述工作均采用的是復合頻域校正方法，本質上屬于低通濾波算法，跟蹤和抗擾性能難以保證，因此，采用先進的多變量控制方法對提升VCA-FSM 控制性能具有重要意義。

滑模控制是一種魯棒性較強的先進控制方法，其對于模型參數不確定性、外部擾動以及系統間耦合擾動等因素具有較強的抑制能力，對于VCA-FSM 系統中的柔性模態、軸間耦合等因素具有較好的控制能力，是提高VCA-FSM 控制性能的理想控制方法之一。但是，需要提及的是，滑模控制的應用主要存在兩方面的技術問題，其一，滑模控制器的高性能控制依賴于精確的系統數學模型；其二，滑模抖振可能會激發系統復雜模態進而影響實際控制效果。

對于上述問題，本文開展了系統辨識、模型降階與滑模控制器設計方面的研究工作，論文的主要內容與貢獻可概述為兩個方面：（1）采用基于脈沖響應的Hankel 矩陣系統辨識方法和基于平衡實現與平衡截斷的模型降階方法，建立了雙軸VCA-FSM 系統的精確耦合模型；（2）設計了積分增廣滑模控制器，并基于VCA-FSM 伺服控制系統實驗平臺對該控制方法進行了測試與評估。

2 VCA-FSM 機理分析與實驗平臺介紹

2.1 VCA-FSM 伺服機構概述與數學模型描述

本文研究對象為1 英寸鏡面的雙軸VCAFSM，其結構如圖1 所示，采用柔性鉸鏈作為支撐結構，VCA 作為驅動元件，四象限探測器（Four-quadrant Detector，QD）作為位 置檢測 元件。該結構具有驅動電壓低、響應速度快、行程范圍大等優點，其偏轉角度范圍可達±1.5°。

圖1 雙軸VCA-FSM 結構Fig.1 Structure of dual-axis VCA-FSM

雙軸VCA-FSM 通過四個圓周分布的VCA來實現反射鏡在水平（X軸）方向和垂直（Y軸）方向上的偏轉。在對控制性能要求不高的系統中，可將VCA-FSM 視為兩個獨立的單輸入單輸出（Single Input Single Output，SISO）系統，即不考慮軸間耦合，以簡化控制系統設計。

軸間耦合是指X軸和Y軸間的運動相互影響，導致系統的控制性能受到限制，這種耦合產生的原因主要有：（1）柔性鉸鏈支撐結構自身的變形以及加工誤差引起的兩個旋轉軸線不垂直；（2）兩對VCA 的坐標軸線與柔性鉸鏈支撐結構旋轉軸線的夾角與45°有偏差；（3）VCA 與反射鏡之間的連接結構導致振動傳遞和受力不均衡等［12-13］。

鑒于上述因素，軸間耦合是不可避免的。因此，在高精密光學系統中，要滿足高性能指標的要求，必須要考慮耦合特性的影響，將雙軸VCAFSM 視為一個雙輸入雙輸出（Double Input Double Output，DIDO）系統，并采取相應的控制策略來克服這些問題。

如圖2 所示為雙軸VCA-FSM 耦合模型，其中ux，uy表示在X軸和Y軸施加的控制電壓；θx，θy表示反射鏡在X軸和Y軸方向上的偏轉角度；Gxx（s）表示控制電壓ux與偏轉角度θx之間的傳遞函數；Gxy（s）表示控制電壓ux與偏轉角度θy之間的傳遞函數；Gyx（s）表示控制電壓uy與偏轉角度θx之間的傳遞函數；Gyy（s）表示控制電壓uy與偏轉角度θy之間的傳遞函數。耦合模型數學描述如式（1）所示：

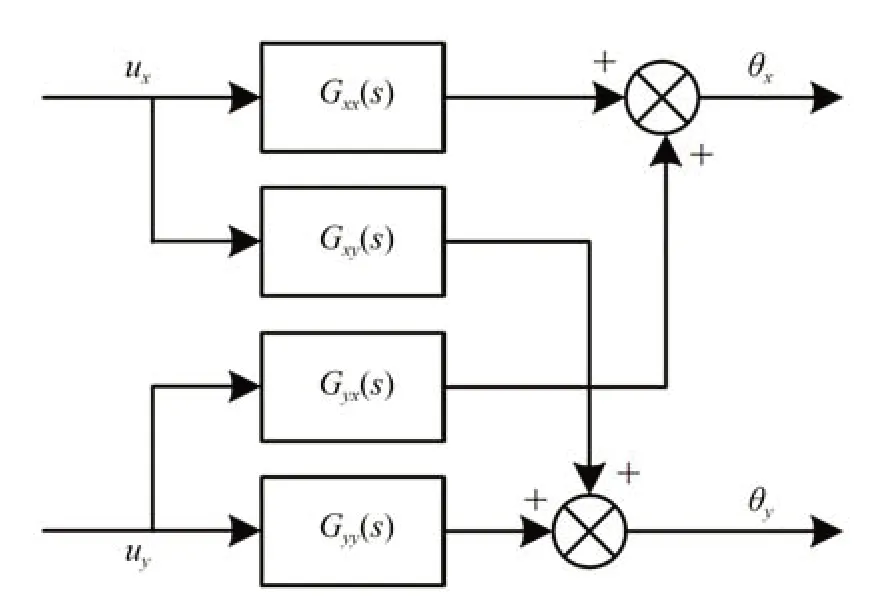
圖2 雙軸VCA-FSM 耦合模型Fig.2 Coupling model of dual-axis VCA-FSM

其中：Ux（s），Uy（s）表示控制電壓ux，uy的拉氏變換；Θx（s），Θy（s）表示偏轉角度θx，θy的拉氏變換。

2.2 VCA-FSM 伺服控制系統實驗平臺介紹

VCA-FSM 伺服控制系統實驗平臺如圖3 所示，主要包括dSPACE，AD/DA，電壓放大驅動電路，VCA，反射鏡及QD 等部件。實驗平臺采用10 kHz 采樣頻率，采樣周期為0.000 1 s，通過上位機軟件Control Desk 實時控制此系統的運行和終止。

VCA-FSM 伺服控制系統的工作原理框圖如圖4 所示。通過QD 輸出由反射鏡的偏轉角度（θx，θy）引起的反饋電壓（Δux，Δuy）；通過實驗平臺的AD 接口采集QD 的輸出信號，并在dSPACE 中解算出伺服機構反射鏡的偏轉角度，與參考信號一起經過控制算法運算后得到伺服機構的控制信號（xin，yin）；通過DA 接口輸出控制信號，并經過電壓放大器放大后（ux，uy）驅動伺服機構的兩對VCA 執行推拉工作，從而實現雙軸閉環控制。

3 VCA-FSM 系統辨識與模型降階

由于VCA-FSM 的柔性模態與復雜耦合特性導致其模型很難被準確描述，這就造成了基于VCA-FSM 自身物理特性建立的數學模型與實際系統無法很好地匹配。而現如今，先進控制方法的應用更加依賴于準確的數學模型，因此，VCA-FSM 的精確建模是滑模控制應用的前提和關鍵條件。下文分別從系統辨識與模型降階兩個方面開展了研究工作，建立了VCA-FSM 的精確耦合模型。

關于雙軸VCA-FSM 的系統辨識與模型降階可理解為對Gxx，Gxy，Gyx，Gyy四個SISO 子系統模型的階次與參數辨識以及對其并聯組合模型的降階，技術方法路線如圖5 所示。

3.1 基于脈沖響應的Hankel 矩陣系統辨識方法

本文在參考文獻［14-15］的基礎上開展VCA-FSM 子系統模型的階次與參數辨識。

設VCA-FSM 子系統的離散狀態空間方程為：

其脈沖響應序列g（k）與系統離散狀態空間方程的參數滿足如式（3）所示的關系：

根據系統脈沖響應構造的d維Hankel 矩陣H與系統離散狀態空間方程參數的關系如式（4）所示：

對d維Hankel 矩陣H進行奇異值進行分解：

其中：U=[u1u2…ud]，V=[v1v2…vd]，σ1≥σ2≥…≥σe?σe+1≥…≥σd≥0。

利用實驗數據構造的Hankel 矩陣通常是非奇異矩陣（即所有的奇異值均大于零），但是大部分的非零奇異值是由于測量噪聲引起的。Hankel 矩陣的奇異值可表征系統各模態在系統中的重要程度，將奇異值從大到小排列，根據奇異值跳變的位置選擇系統的階次，故選擇系統階次為e。

根據確定的系統階次，將Hankel 矩陣H奇異值分解的結果進一步分解：

其中：U1=[u1u2…ue]，V1=[v1v2…ve]，∑1=diag{σ1σ2…σe}。

其中：E1表示矩陣的第一行，E1表示矩陣的第一列。

根據式（4），再構建新的d維Hankel 矩陣H1：

綜上，可確定VCA-FSM 子系統的離散數學模型。利用Matlab 軟件中的d2c 函數將離散數學模型轉化為連續時間數學模型，以方便后續的模型降階及滑模控制系統設計。

3.2 VCA-FSM 系統辨識

基于圖3 所示的實驗平臺開展系統辨識實驗。

選取兩個周期的幅值為5 mV、階次為14 的偽隨機序列作為激勵信號。給X軸施加激勵信號，Y軸自由；給Y軸施加激勵信號，X軸自由，X軸和Y軸響應如圖6 所示。可以看出，反射鏡在X（或Y）軸方向VCA 的驅動下繞X（或Y）軸偏轉的同時，在Y（或X）軸方向上產生了較大的耦合運動。

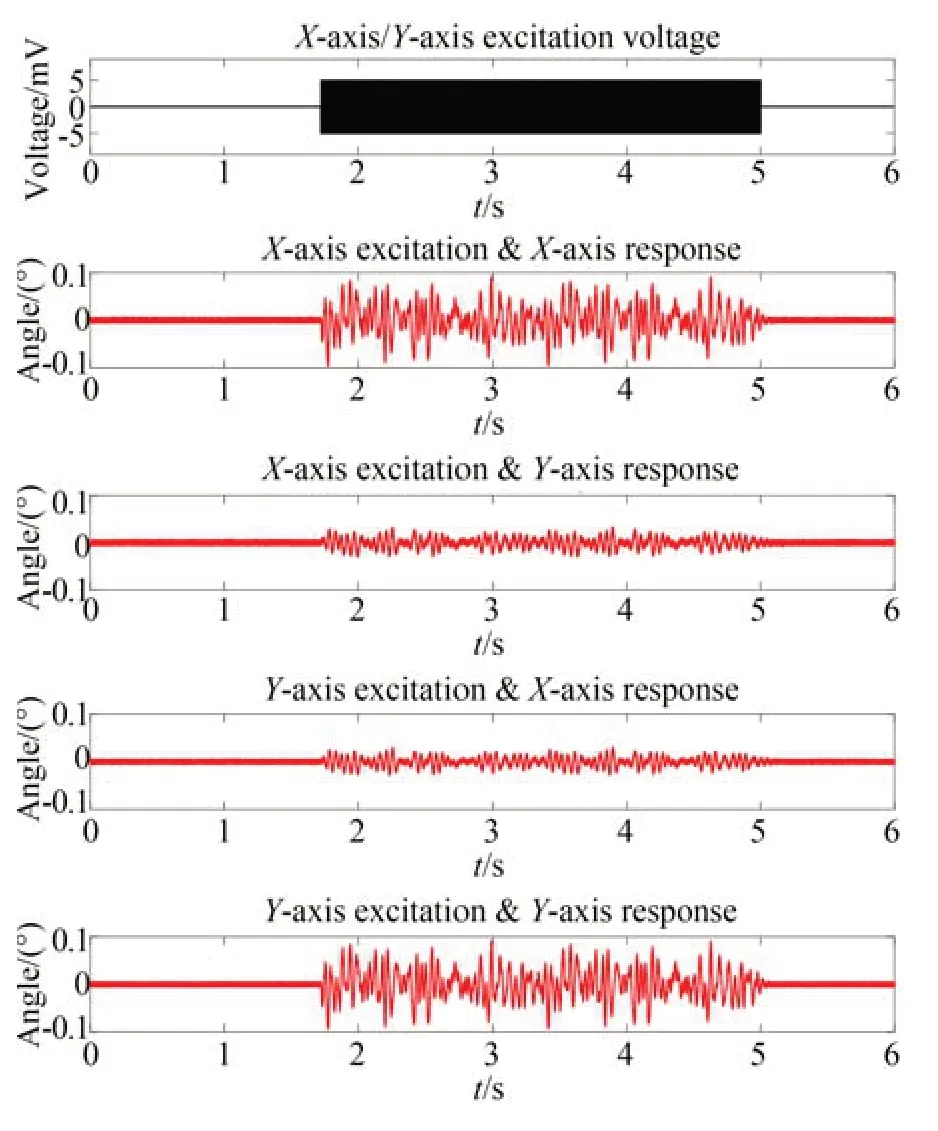
圖6 激勵信號與響應信號曲線Fig.6 Excitation signal &response signal curve

VCA-FSM 從靜態轉變為偽隨機信號激勵下的動態過程中存在過渡過程，會導致模型參數計算不準確，因此根據第二個周期的實驗數據，分別針對Gxx，Gxy，Gyx，Gyy四個SISO 子系統開展系統辨識。Hankel 矩陣的奇異值如圖7 所示，選擇四個SISO 子系統模型的階次均為4。

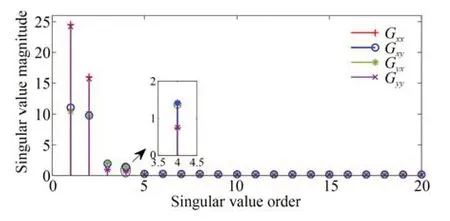
圖7 Hankel 矩陣奇異值Fig.7 Singular value of the Hankel matrix

由此，根據式（7）和式（9）可確定系統離散數學模型，通過Matlab 連續化后，得到其對應連續系統數學模型的狀態空間實現分別為：

基于線性子系統并聯組合理論［16］，得到雙軸VCA-FSM 系統DIDO 耦合模型的狀態空間實現為：

3.3 VCA-FSM 模型降階

通過上述辨識方法得到的雙軸VCA-FSM系統的DIDO 耦合數學模型階次為Gxx，Gxy，Gyx，Gyy四個子系統模型階次之和，即耦合系統模型階次為16，高階次模型會導致滑模控制系統設計復雜、數字控制系統難以實現等問題。因此，有必要對VCA-FSM 系統的高階次數學模型進行降階。

本文在參考文獻［17-18］的基礎上開展VCA-FSM 系統DIDO 耦合模型的降階。

系統（11）的能控性格拉姆矩陣Lc與能觀測性格拉姆矩陣Lo滿足以下李亞普諾夫方程，其中Lc與Lo均為正定矩陣［19］。

存在線性非奇異平衡變換矩陣T，使得變換后系統的能控性格拉姆矩陣與能觀測性格拉姆矩陣滿足以下關系：

其中：Λ=diag{λ1λ2…λN}，其對角元素為系統奇異值，且λ1≥λ2≥…≥λr?λr+1≥…≥λN≥0。

變換后系統的平衡實現模型為：

系統模型平衡實現后，根據系統奇異值的大小對所得到的平衡模型進行平衡截斷，保留奇異值相對較大的這部分系統，故選擇降階系統的階次為r，從而得到平衡截斷后的降階模型。

其中，Gr維數為r。

根據上述降階方法，得到VCA-FSM 系統平衡實現模型的奇異值如圖8 所示。

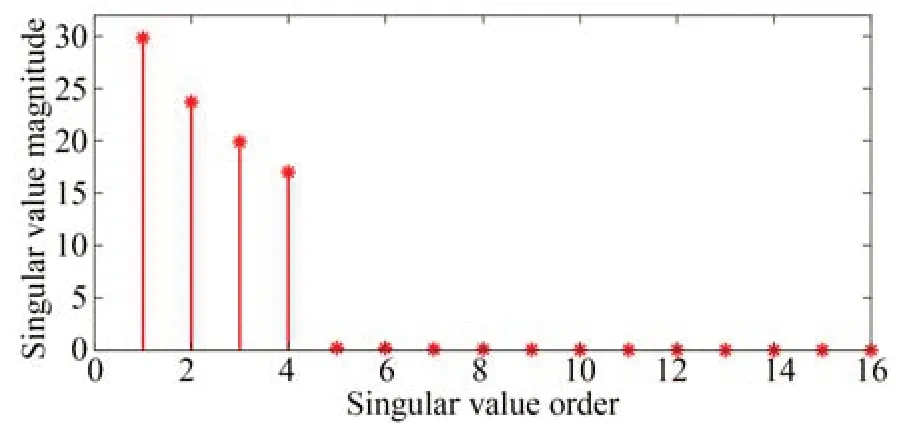
圖8 系統平衡實現模型的奇異值Fig.8 Singular value of system's balanced realization model

選擇降階模型的階次為4，得到降階模型的狀態空間實現為：

式（16）所示的降階模型（綠色實線）、式（10）所示的辨識模型（藍色實線）與真實系統（紅色實線）的頻率特性曲線對比如圖9 所示(彩圖見期刊電子版）。

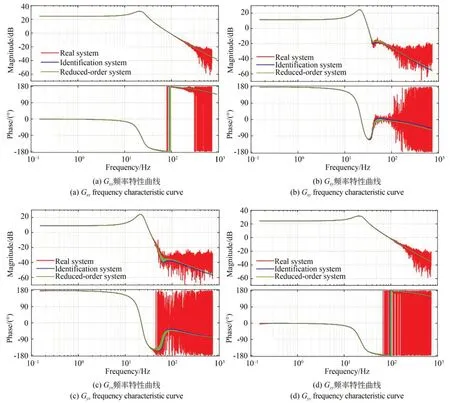
圖9 降階前后模型與實際系統的頻率特性對比曲線Fig.9 Comparison curves of frequency characteristic of the model and the actual system before and after the reduction

根據圖9 可得：（1）基于脈沖響應的Hankel矩陣系統辨識方法建立的系統模型能夠充分表征系統的幅頻特性與相頻特性；（2）基于平衡實現與平衡截斷模型降階方法得到的降階模型與未降階模型的頻率特性具有極高的相似性，可滿足高性能控制系統的設計需求；（3）系統存在強耦合特性，且系統在80 Hz 后出現了較大的不確定性，這對控制系統的設計帶來了很大挑戰，控制器必須具有一定的魯棒性，以保證系統的穩定控制。

4 控制器設計

4.1 積分增廣滑模控制器設計

VCA-FSM 的DIDO 耦合模型是通過系統辨識與模型降階得到的，所得模型的狀態變量并無實際物理意義，因此無法直接通過控制狀態變量使系統實現對參考信號的跟蹤。為了實現跟蹤，根據內模原理，引入積分環節，構成積分增廣的系統，使增廣后的系統具有跟蹤性能。

根據系統降階模型的狀態空間實現（16），其對應的狀態空間方程可寫為：

其中：Ar為n×n矩陣，Br為n×m矩陣，Cr為l×n矩陣。

要求系統輸出y（t）跟蹤參考信號yd（t），定義偏差信號為e（t），對偏差信號進行積分，其數學描述為：

對式（18）求導可得：

由于積分器的引入使原系統升階，故可將積分器的輸出η選作附加的狀態變量，從而對原系統進行增廣，得到積分增廣后的系統模型為：

積分增廣后，系統由原來的n維變為了n+l維，為了能夠采用滑模控制，且能夠獲得穩定的、動態性能滿意的系統，必須要求增廣后的系統能控。

已知rank[B AB A2B A3B A4B A5B]=6，由系統能控性秩判據可知，增廣系統能控，故可對積分增廣后的系統進行滑模控制器設計。

設計一個滑模控制器主要包括兩個部分：（1）設計切換函數s，保證其所確定的滑模運動漸進穩定，且具有良好的動態品質；（2）設計控制律u，該控制必須滿足可達性條件，即使得系統的狀態運動點能夠在有限時間內被驅動到切換面（s=0）上。

4.1.1 滑模切換函數設計

設切換函數為：

其中，M為l×（n+l）切換函數系數矩陣。則滑模控制系統沿切換面進行滑模運動時的滑模方程為：

已知rankB=m，故存在非奇異線性變換x=P-1，使增廣系統（20）轉換為如下簡約型［20］：

同時，其相應的切換面變換為：

將式（25）代入式（23），可得：

式（26）與式（22）完全等價，從而滑模控制系統可等價為如式（26）所示的降階方程。

由（A，B）能控，可得出必是能控的［16］。因此系統（26）的極點可由K任意配置。結合式（24），可得切換函數系數矩陣M為：

顯然，切換函數（21）的設計可以保證其所確定的滑模運動漸進穩定，且具有良好的動態品質。

4.1.2 滑模控制律設計

為了保證滑模運動的存在，滑模控制律必須滿足可達性條件：

為了滿足可達性條件并消除滑模抖振，本文采用改進指數趨近律方法。傳統指數趨近律如下：

傳統指數趨近律雖能夠有效抑制滑模抖振，但卻無法將其消除，為消除抖振，本文采用連續函數sgmf(s)=替代符號函數sgn（s）。

改進指數趨近律如下：

其中：ε＞0，k＞0，α＞0。ε，k，α是改進指數趨近律的三個參數，可通過設置ε，k，α的取值，調整滑模控制的趨近過程。

由改進指數趨近律（30），可得出滿足可達性條件（28）的滑模控制律u：

求得滑模控制律u為：

穩定性分析：滑模控制系統存在著特殊的滑模運動。當s=0 時，系統沿著切換面進行滑模運動，只要適當地如式（27）設計M就能保證系統（22）的穩定性；當s≠0 時，設計李亞普諾夫函數V（x）=s2，因滑模控制律u始終保證式（28）成立，故(x)≤0。可見以上滑模控制系統漸進穩定。

4.2 狀態觀測器設計

在積分增廣滑模控制器的設計中，滑模切換函數與控制律均由積分增廣系統的全維狀態變量構造。對于積分增廣系統（20），狀態變量η為跟蹤誤差的積分，可測量；狀態變量xr是原系統的狀態變量，不具實際物理意義，無法測量。因此，為實現滑模控制，可針對積分增廣系統設計降維狀態觀測器，此時，觀測器僅針對原系統（17）進行狀態估計。

狀態觀測器的形式如下：

其中，L為調節漸進于xr的反饋增益矩陣。

利用觀測器理論，在狀態xr不可測的情況下，即不能構造切換函數s=Mx時，根據估計出的狀態來代替xr，從而構造出漸進的切換函數：

根據分離原理［16］，基于極點配置的滑模控制器設計與狀態觀測器設計可以分開進行，所以其相應的滑模控制律可變為：

因此，針對增廣系統（20），采用狀態觀測器（33）、切換函數（34）和控制律（35）的設計方案，可確保控制系統的穩定性［20］，并可實現對參考信號的跟蹤。

雙軸VCA-FSM 滑模伺服控制系統結構框圖如圖10 所示。

圖10 雙軸VCA-FSM 滑模控制系統結構框圖Fig.10 Structure diagram of dual-axis VCA-FSM sliding mode control system

5 實驗驗證與分析

本部分基于VCA-FSM 數學模型設計控制系統，并開展了頻域與時域性能測試實驗［21］。為證明雙軸滑模控制（Dual-axis Sliding Mode Control，D-SMC）方法的有效性和先進性，將其與單軸滑模控制（Single-axis Sliding Mode Control，SSMC）和PID 控制方法進行對比。

特殊說明的是，本研究開展的是較大行程的控制實驗，若縮小偏轉角度范圍，可通過調整控制器參數，增加控制器增益，進一步提高系統的控制性能。

5.1 實驗參數設定

根據閉環頻率特性和階躍響應表現，經過多次實驗調整，最終確定PID 控制器的參數為：Kx=Ky=0.06+

需要強調的是，具體參數選擇需要根據實際系統的特性和性能要求進行調整。不同系統的參數需求可能有所不同，因此，在實際應用中，需要通過實驗調整來確定最佳的參數值，以實現所需的控制性能。以上提到的參數值僅作為本次研究的一個示例。

5.2 伺服控制實驗

基于圖3 所示的VCA-FSM 伺服控制系統實驗平臺，對上述三種不同控制系統進行了頻域和時域性能測試，并分別從閉環跟蹤帶寬、軸間耦合閉環頻率特性、擾動抑制帶寬、階躍響應動態性能、軸間耦合運動特性及螺旋線跟蹤精度等方面全面評價了控制方法的控制性能。

5.2.1 頻域性能測試

（1）閉環頻率特性

X軸參考信號（θxd）為幅值0.15°、頻率0.1～1 000 Hz 的正弦 掃頻信 號，Y軸參考信號（θyd）為0，X-X軸 和X-Y軸頻率 特性曲 線如圖11（a）和圖11（b）所示；Y軸參考信號為幅值0.15°、頻率0.1～1000 Hz 的正弦 掃頻信 號，X軸參考 信號為0，Y-X軸和Y-Y軸頻率特性曲線如圖11（c）和圖11（d）所示，X軸和Y軸的閉環頻域性能表現幾乎一致。

從圖11（a）和圖11（d）可以看出，三種不同控制方法下系統的X軸閉環跟蹤帶寬（-3 dB）分別為141 Hz，94 Hz 和40 Hz；Y軸閉環跟蹤帶寬分別為140 Hz，93 Hz 和40 Hz，D-SMC 相比于SSMC 和PID 的閉環跟蹤帶寬分別提升了約50.3% 和251.3%，且D-SMC 方法下伺服系統的閉環跟蹤帶寬遠大于系統不確定性出現的頻率（80 Hz），這表明D-SMC 方法具有很強的魯棒性。

從圖11（b）和圖11（c）可以看出，D-SMC 和SSMC 方法下系統的X-Y軸耦合和Y-X軸耦合的幅頻特性曲線均位于-20 dB 以下，系統的軸間耦合基本消除，通過控制實現了解耦，而PID 控制方法下系統X軸和Y軸間仍存在較大的耦合。

一般情況下，增加PID 控制器的增益可以提高控制帶寬。但是，根據頻率特性曲線，PID 控制系統存在一個較大的諧振峰值，約為10 dB@30 Hz。如果進一步增加PID 控制器的增益，系統可能存在諧振峰值超過限制行程的安全隱患，且會導致時域性能變差，這是由系統本身特性決定的。綜上所述，表明本文中PID 控制器的參數設置是合理的。

（2）抗擾頻率特性

X軸 和Y軸參考 信號均 為0，X軸干擾信號（dx）為幅值0.015°、頻率0.1～1000 Hz 的正弦掃頻信號，Y軸干擾信號（dy）為0，dx-ex幅頻特性曲線如圖12（a）所示；Y軸干擾信號為幅值0.015°、頻率0.1～1000 Hz 的正弦掃頻信號，X軸干擾信號為0，dy-ey幅頻特性曲線如圖12（b）所示，X軸和Y軸的抗擾性能表現幾乎一致。

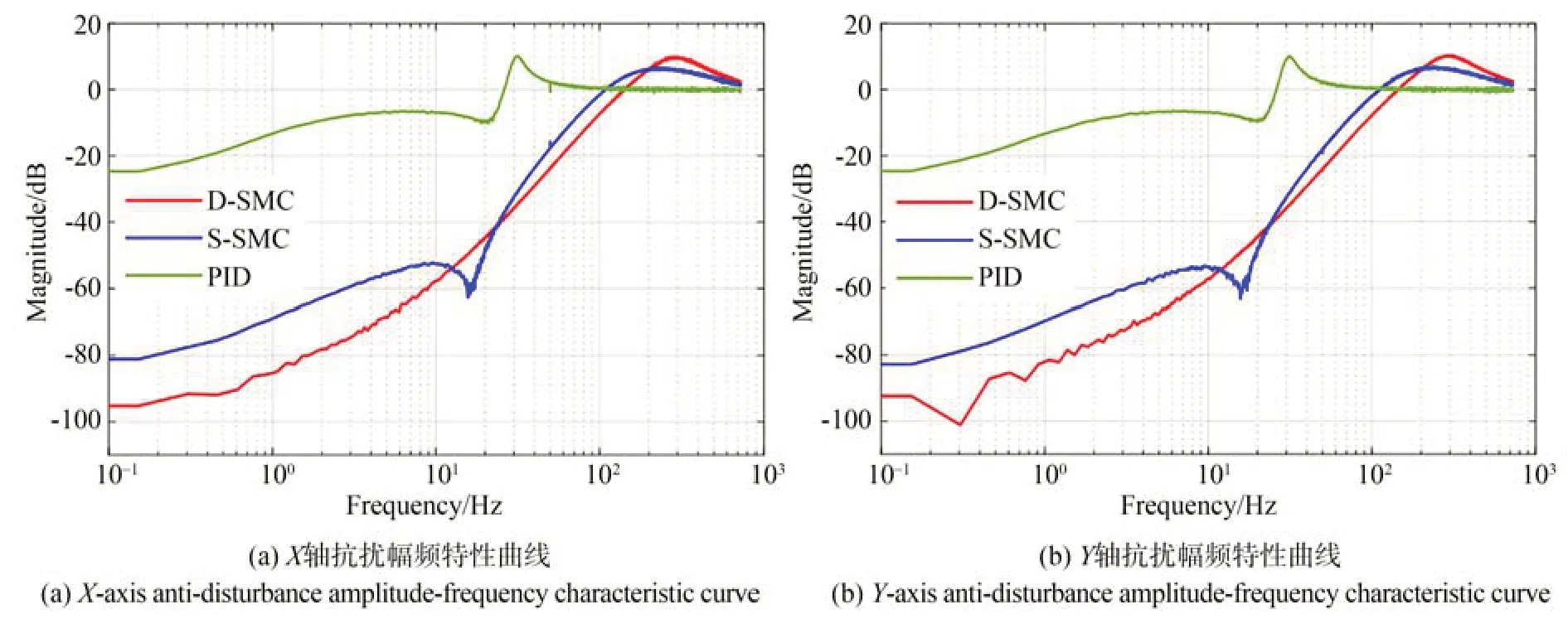
圖12 抗擾幅頻特性曲線Fig.12 Anti-disturbance amplitude-frequency characteristic curve

從圖12 可以看出，三種不同控制方法下系統的X軸擾動抑制帶寬（0 dB）分別為142 Hz，109 Hz 和26 Hz；Y軸擾動 抑制帶 寬分別 為145 Hz，112 Hz 和26 Hz，D-SMC 相比于S-SMC 和PID的擾動抑制帶寬分別提升了約39.9% 和451.9%。

5.2.2 時域性能測試

（1）階躍信號響應

分別給X軸和Y軸在不同時刻參考幅值為0.3°的階躍信號，三種不同控制方法下系統的X軸和Y軸的階躍響應曲線如圖13 所示，X軸和Y軸的時域階躍性能表現幾乎一致。

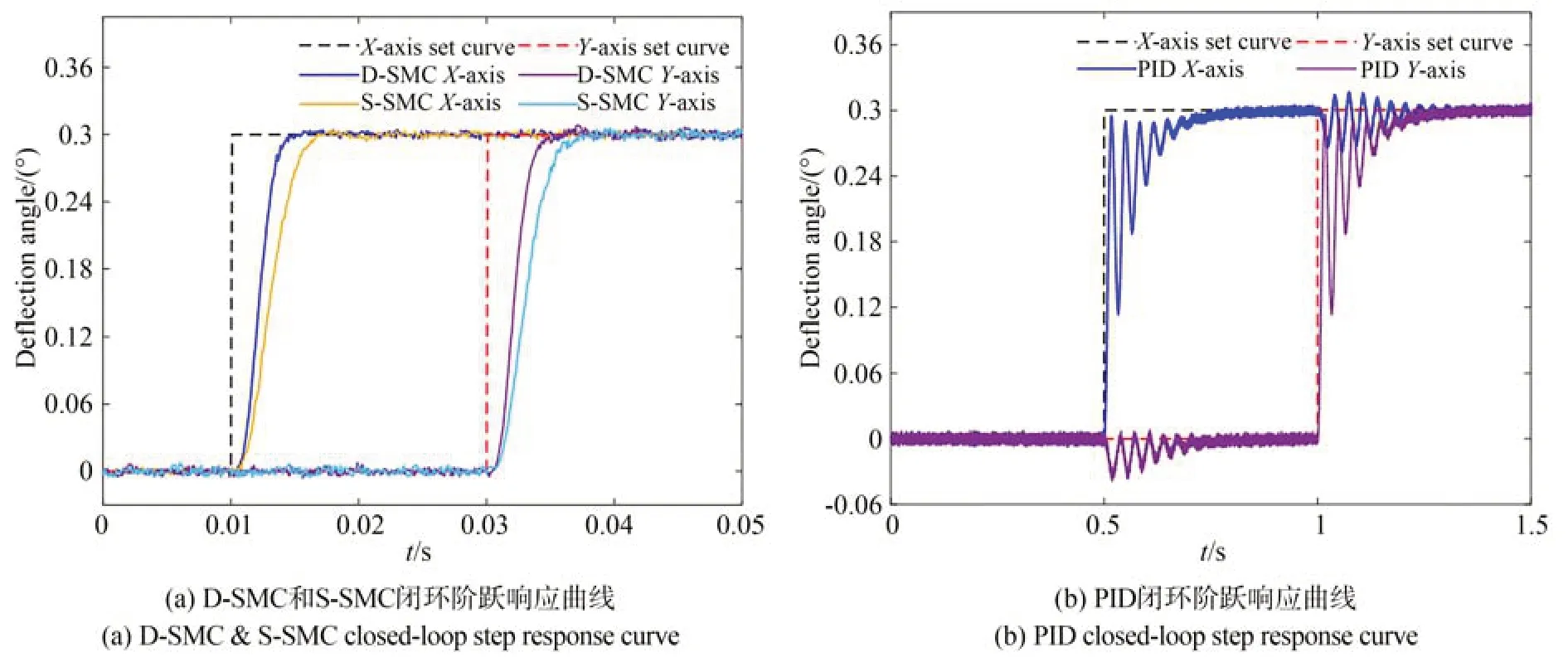
圖13 閉環階躍響應曲線Fig.13 Closed-loop step response curve

以±5%誤差帶為標準，三種不同控制方法下系統的X軸調節時間分別為3.9 ms，5.6 ms 和172.6 ms；Y軸調 節時間分別為3.9 ms，5.5 ms和173.2 ms，D-SMC 相比于S-SMC 和PID 的調節時間分別縮短了約29.7% 和97.7%。且DSMC 和S-SMC 方法下系統的X軸和Y軸間的運動基本互不影響，運動耦合特性得到大幅改善，而PID 控制方法下系統的X軸和Y軸間的運動互相影響很大，仍存在較大耦合。

（2）螺旋線信號跟蹤

螺旋線信號方程為：

其中：r為極坐標半徑，θ為極坐標角度。a=π×0.3°，b=360°×5，t為0～1 s 變化的時間參數。跟蹤螺旋線信號實驗結果如圖14 所示。

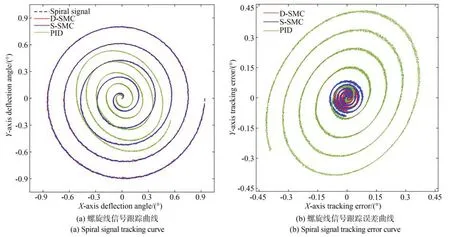
圖14 螺旋線信號跟蹤結果Fig.14 Result of spiral signal tracking

定義平 均絕對誤差（Mean Absolute Error，MAE）：

三種不同控制方法下系統的MAE 分別為0.000 46°（1.7″），0.000 93°（3.3″）和0.021°（75.6″），D-SMC 相比于S-SMC 和PID 的跟蹤精度（MAE）分別提高了約48.5%和97.8%。

5.3 小結

根據上述實驗，D-SMC、S-SMC 和PID 控制下，控制系統頻域與時域關鍵性能指標匯總如表1 所示。

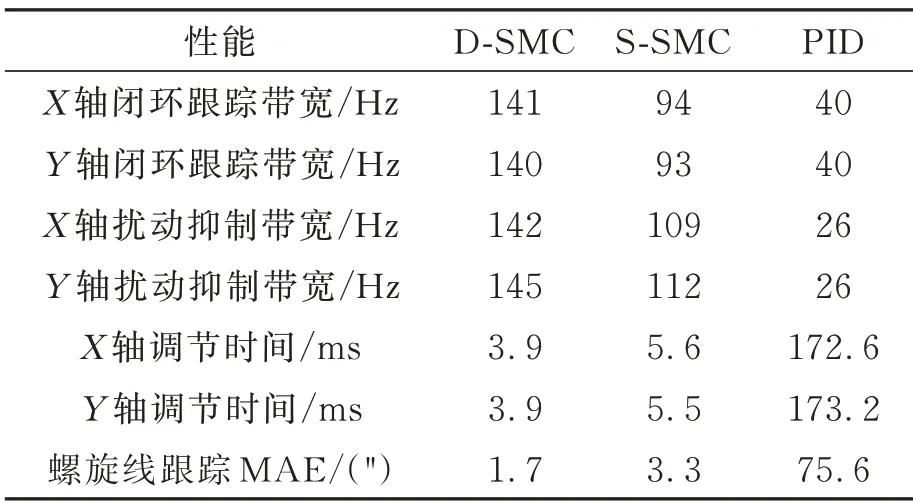
表1 VCA-FSM 伺服控制系統頻域、時域性能Tab.1 Time domain &frequency domain performance of VCA-FSM servo control system

實驗結果表明，本文提出的D-SMC 方法相較于S-SMC 和PID 方法，在閉環帶寬、抗擾性、動態響應和控制精度等方面都取得了顯著提升，充分證明了D-SMC 方法的先進性和優越性。

6 結論

本文圍繞對存在強耦合特性雙軸VCAFSM 的高性能控制問題開展了研究工作，提出了基于系統辨識與模型降階的積分增廣滑模控制方法。首先介紹了VCA-FSM 與伺服控制系統實驗平臺工作原理，然后通過系統辨識與模型降階建立了雙軸VCA-FSM 的精確耦合模型，最后設計了雙軸積分增廣滑模控制器，并通過伺服實驗對其進行了性能測試。

實驗結果表明，本文提出的雙軸VCA-FSM滑模控制方法有效地消除了X軸和Y軸控制回路間的耦合現象，且控制效果明顯優于不考慮耦合的單軸滑模和PID 控制方法，其對系統的不確定性和擾動的魯棒性更強，可以保持系統的穩定性和控制精度。D-SMC 控制下，系統頻域與時域的各項性能均得到了大幅度的提高，其中，閉環跟蹤帶寬達到140 Hz，擾動抑制帶寬可達到142 Hz，階躍響應調節時間達到3.9 ms，螺旋線軌跡跟蹤精度達到1.7″。研究證明了D-SMC 方法的有效性和先進性。

本文所提控制方法能夠實現對VCA-FSM這類具有強耦合特性被控對象的高性能控制，為提高VCA-FSM 的控制性能提供了一種有效手段，對實際的工程應用具有一定指導作用。