基于單快拍MUSIC與改進UTJDL的海雜波抑制算法

韓文強,李慶忠,牛 炯

(1. 中國海洋大學 工程學院, 山東 青島 266100)

(2. 聯想集團 摩托羅拉移動通信技術有限公司, 湖北 武漢 430223)

0 引 言

船載高頻地波雷達(HFSWR)[1]具備很強的靈活機動性,有效擴大了雷達的探測范圍,廣泛用于監測開放海域的艦船目標。對于船載HFSWR,由于海浪與平臺運動的相互作用,海洋回波特性相對于岸基HFSWR更加復雜,前向運動會引起回波多普勒譜中的一階海雜波展寬,導致展寬域中的目標被掩蓋[2],對位于展寬域中的低速小目標檢測非常不利。此外,在海浪的作用下,船載平臺的六自由度周期性運動會在多普勒域產生附加峰,同樣會影響目標的檢測性能。因此,船載HFSWR的關鍵技術就是如何有效抑制展寬的海雜波和六自由度運動產生的附加峰,以實現對目標多普勒頻率和方位的快速、準確檢測。

目前船載HFSWR的目標檢測方法主要包括運動補償方法[3],基于預測相消模型(PC)的時域濾波算法[4],空域中的波束形成(DBF)方法[5-6]、正交加權(OW)方法[7]、斜投影(OP)[8]算法,以及空時自適應處理(STAP)[9]方法等。此外,利用深度學習技術進行海雜波抑制和海面目標檢測也是目前研究的一個熱點,如文獻[10]提出了一種基于INet的導航雷達圖像雜波抑制和海面動目標檢測方法,并利用實測數據測試和驗證了模型檢測海面動目標的實時性和準確性,取得了較好的檢測效果,但尚未考慮船載平臺復雜運動對海雜波的影響。在以上諸多方法中,目前最有前景的方法是降維STAP方法,其中局域聯合處理(JDL)[11]算法是目前的研究熱點。

傳統JDL算法在估計雜波協方差矩陣時,要求不同距離單元之間,海雜波應服從獨立同分布。但對于船載HFSWR,由于船載平臺前向運動會引起回波入射角隨時間的變化,且不同距離元的回波入射角變化規律不同,導致不同距離單元間海雜波的分布特性不同[12-13],因此利用傳統JDL算法估計雜波協方差矩陣時,就會出現估計精度惡化的問題。為克服這一問題,出現不少改進JDL算法。如文獻[14]提出了一種利用距離維相關性系數加權的改進JDL算法,在估計被測距離單元雜波協方差矩陣時,通過相關系數確定訓練樣本的權重,以提高估計精度。文獻[15]為了提高方位估計精度,首先利用多重信號分類(MUSIC)算法對待測距離單元進行方位處理,然后再利用JDL算法進行海雜波抑制,但MUSIC算法的精度需要大量快拍數據來支持,由于長時間相參積累導致快拍數過多,使其時間復雜度太高,或處理效率很低。對此,文獻[16]提出一種單快拍MUSIC預處理的海雜波抑制算法,文獻[17]提出一種高分辨稀疏表示的雜波抑制算法,但是以上方法對非均勻雜波抑制能力較差。此外,文獻[14]利用無跡變換(UT)從單個距離單元的數據中,獲得更多可用的訓練樣本,以粗略逼近感興趣距離單元的雜波協方差矩陣。但是在其UT算法的矩陣計算中,要求被分解矩陣必須為正定對角矩陣,此條件在實際中往往無法滿足,由此會造成濾波計算時存在較大誤差[18]。

總之,改進JDL算法是目前最有前景的算法,但仍然存在兩方面問題。一方面,為提高MUSIC算法方位估計精度,需要大量快拍數據集來支持,因此處理效率較低。另一方面,通過預處理來增加訓練樣本數據的UT算法,對分解矩陣要求過高而無法適應實際數據的特點。

針對以上改進JDL存在的兩個問題,本文提出了一種單快拍MUSIC與改進UTJDL結合的海雜波抑制算法。為克服MUSIC算法需要大量快拍數據支持的問題,本文首先通過單快拍MUSIC算法得到不同距離單元的角度-多普勒數據,以實現對信號源的精準估計;然后,利用基于奇異值分解(SVD)的方法對UT算法中的矩陣計算進行了改進,避開了對分解矩陣要求苛刻的條件,并利用改進的UT方法對每個距離元的JDL數據進行預處理,從而獲得更多的一致性數據;最后,根據不同距離單元與待檢測距離單元的相關系數估計待測距離單元的協方差矩陣,并由此實現對海雜波的快速有效抑制。

1 單快拍MUSIC與改進UTJDL結合的海雜波抑制算法

根據以上分析,本文提出的船載海雜波抑制算法的整體流程如圖1所示。該算法主要由兩個模塊組成,一是利用單快拍MUSIC算法,大大降低了傳統MUSIC算法對過多快拍數的依賴,并實現了對目標角度的準確估計;二是利用基于SVD的UT算法解決了傳統UT算法中非正定矩陣導致的濾波發散問題。下面具體介紹各個模塊的具體實現過程。

圖1 海雜波抑制算法流程圖

1.1 單快拍MUSIC算法

由于傳統MUSIC算法的性能受快拍數的影響較大,快拍數越多,波達方向(DOA)估計越準確,但是大的快拍積累會造成很大的運算量,不利于實際工程應用[19],因此本文利用單快拍MUSIC將陣列信號轉換成角度多普勒域的信號,進而再利用后續的濾波算法進行雜波抑制,在保證DOA估計精度的同時,可以大大降低運算量。單快拍MUSIC算法步驟如下:

(1) 通過構建Toeplitz矩陣[20]得到式(1)所示的協方差矩陣。

(1)

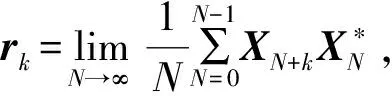
(4) 根據MUSIC算法譜估計公式[19]進行譜峰搜索。

根據以上步驟即可將陣列信號轉換到角度多普勒域,得到輸入數據PMUSIC。在特定的頻率上,峰值最大處即對應著目標所處的方位。

1.2 基于SVD的UT算法

UT是一種采用確定采樣策略逼近非線性分布的統計信息的方法[18]。其原理是根據輸入變量的均值和方差,使用一定規則和數量的樣點集稱作Sigma點,用于模擬輸入變量的分布,然后將Sigma點代入非線性系統,得到相應的輸出點集,從而得到估計的均值和方差。

由于傳統UT算法在計算Sigma點時需要用到Cholseky分解,其前提條件是被分解矩陣必須為正定對角矩陣,此條件在實際中往往無法滿足,由此造成濾波計算時存在較大誤差。因此,本文采用基于SVD的UT算法。對于船載HFSWR數據,假設距離單元r處,ηa×ηb維大小的角度-多普勒局域(LPR)數據經過向量化處理后得到ηaηb×1維數據xLPR,其均值和協方差分別為mx和Rx。通過均值mx和協方差Rx可以獲得2ηaηb+1個Sigma點及相應的權值,即

(2)

(3)

(4)

(5)

在以上步驟中,SVD在矩陣負定時依然能夠正確分解,表現出比Cholseky分解更好的穩定性[18,21]。

1.3 基于單快拍MUSIC和改進UTJDL的海雜波抑制算法

本文提出的船載HFSWR海雜波抑制算法主要由以下步驟組成。

(1)利用單快拍MUSIC算法把陣列-距離-多普勒數據轉換為距離-角度-多普勒域數據PMUSIC。如圖2所示,將PMUSIC作為輸入數據,選取PMUSIC距離r處的角度-多普勒數據,選取大小為ηa×ηb的LPR數據xLPRr,并將數據進行向量化。

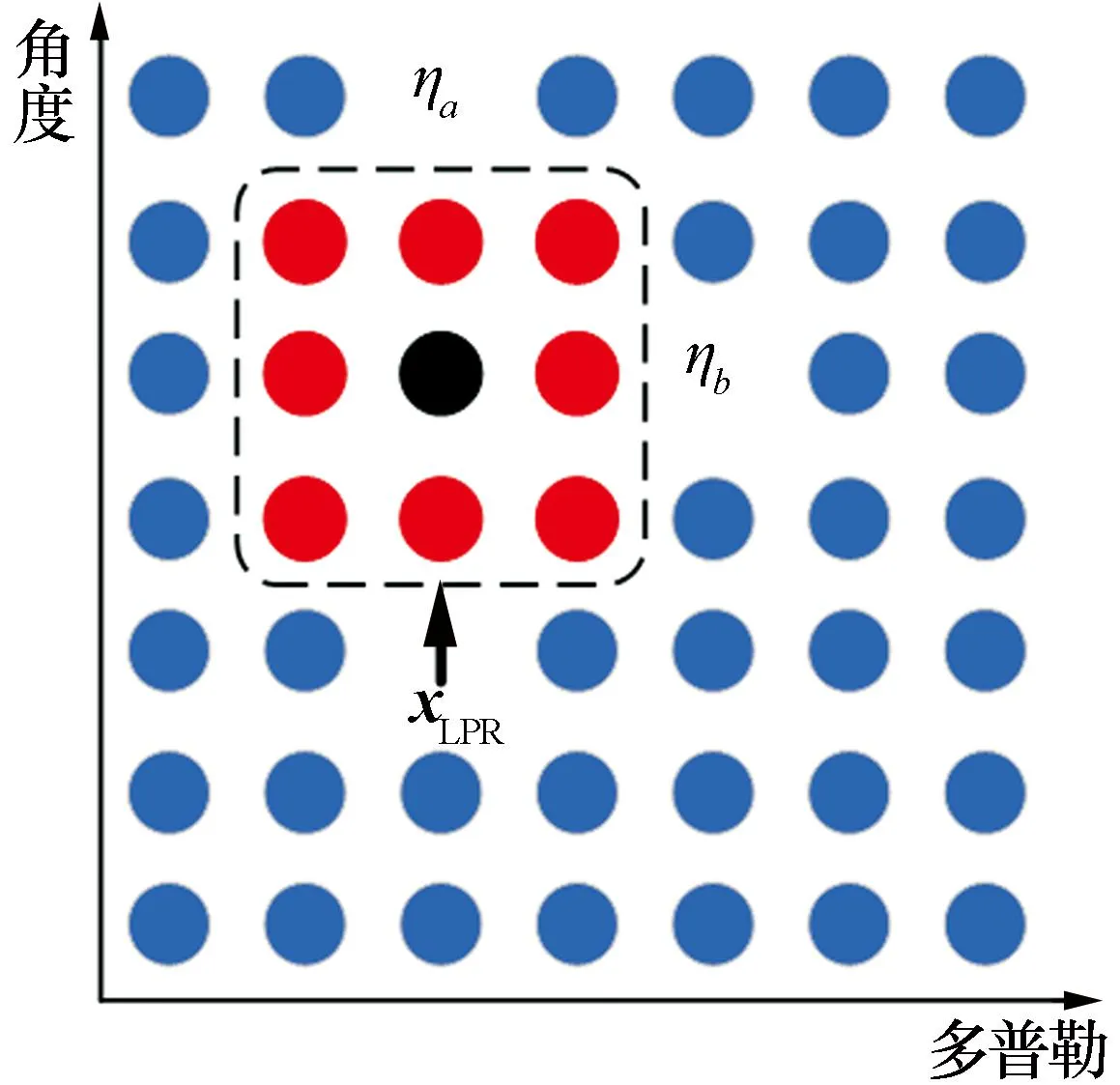
圖2 改進JDL算法中的LPR

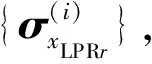
(3) 估計訓練樣本與待測距離單元之間的相關系數。為提高待測距離單元協方差矩陣估計的準確性,本文首先估計樣本距離元與待測距離單元之間的相關性,具體步驟如下:

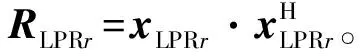
步驟2 對RLPRr進行特征分解,然后選取最大特征值對應的特征向量,將選取的特征向量進行歸一化后記作ζr。

步驟3 對于訓練樣本所在的距離單元,重復步驟1、步驟2,得到對應的ζi。

(4) 通過式(6)獲得待測距離單元的協方差矩陣。

(6)

式中:ρi表示第i個距離單元的估計樣本與待測距離單元之間的相關性系數;Ryi為第i個距離單元通過改進UT算法獲得的估計樣本協方差矩陣。

(5) 構建轉換矩陣Tst和LPR內的空時導向矢量。

Tst=[hv⊙st(f-1),hv⊙st(f0),hv⊙st(f1)]?

[ss(φ-1),ss(φ0),ss(φ1)]

(7)

式中:Tst轉換矩陣由空間導向矢量和時間導向矢量進行Kronecker積得到;st(φ)為輸入數據的時間導向矢量;ss(f)為輸入數據的空間導向矢量;hv為漢寧窗。

根據式(8)即可獲得LPR內的空時導向矢量

(8)

其中

s=st(f0)?ss(φ0)

(9)

式中:s為單個距離單元空時數據的空時導向矢量。

(10)

利用自適應權值向量可以獲得修改的樣本矩陣求逆(MSMI)統計量

(11)

該統計量即代表特定角度-多普勒單元的估計值。為了獲得全部角度-多普勒區域的估計值,通過對角度和多普勒進行遍歷,即可達到在角度-多普勒域進行雜波抑制的目的。

2 實驗結果與分析

為驗證本文算法對船載HFSWR一階海雜波及附加峰的抑制效果及目標檢測的準確性,本文利用仿真數據和實測數據對提出的算法進行了實驗驗證,并與其他雜波抑制算法進行了性能比較。

本文采用信雜噪比(SCNR)[12]作為評價指標,衡量各種算法對海雜波的抑制效果。雜波抑制前后SCNR的提升量SCNRimprove越大,代表雜波抑制效果越好,反之則抑制效果越差。雜波抑制前后SCNR提升量為

SCNRimprove=SCNRafter-SCNRbefore

(12)

(13)

式中:Ps表示感興趣多普勒單元處信號的功率;Pc+n表示雜波加噪聲的功率。

2.1 仿真海雜波抑制實驗結果

本節根據文獻[12]提出的海雜波模型對海雜波三維數據進行了仿真。表1給出的是仿真模型所用參數,其中d為陣元間距,M為脈沖積累個數,N為陣元數目,A1和A2都是瑞利分布隨機變量,λ為雷達波長,Tr為脈沖重復周期,fc為雷達發射信號載波頻率,Vp表示船前向行駛速度,rmax表示雷達最大探測距離。表2給出的是三自由度擺動運動的相關參數。為了更好地對海雜波進行仿真,在仿真模型中加入了20 dB的高斯白噪聲。

表1 模型參數列表

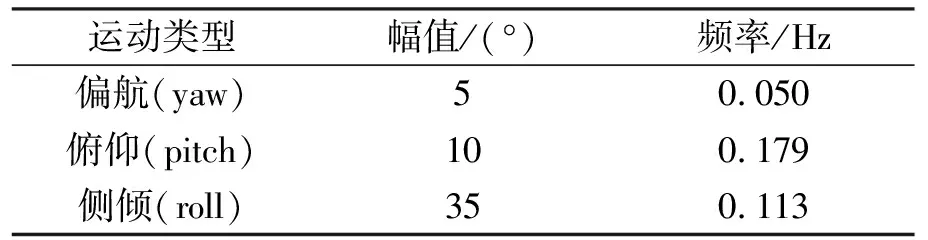
表2 三自由度擺動參數

當船載平臺速度Vp=4 m/s時,海雜波仿真結果如圖3所示,其中圖3a)為得到的距離-多普勒(RD)譜,圖3b)為角度-多普勒(AD)譜,圖3c)為仿真目標所在距離單元的多普勒截面。可見,當船載平臺前向運動時,一階海雜波展寬嚴重,目標被掩蓋在展寬的一階海雜波之中。因此,船載海雜波的抑制是實現目標準確檢測的關鍵。

圖3 海雜波數據仿真結果

圖4是本文算法與DBF[5]、JDL[11]及UTJDL[12]算法對仿真海雜波抑制與目標檢測的AD譜對比結果。當船載平臺速度Vp=4m/s時,本文分別在距離為50 km,方位角為60°,頻率為-0.318 0 Hz和0.176 7 Hz處添加兩個目標。此外,仿真目標的輸入SCNR均為-30 dB。

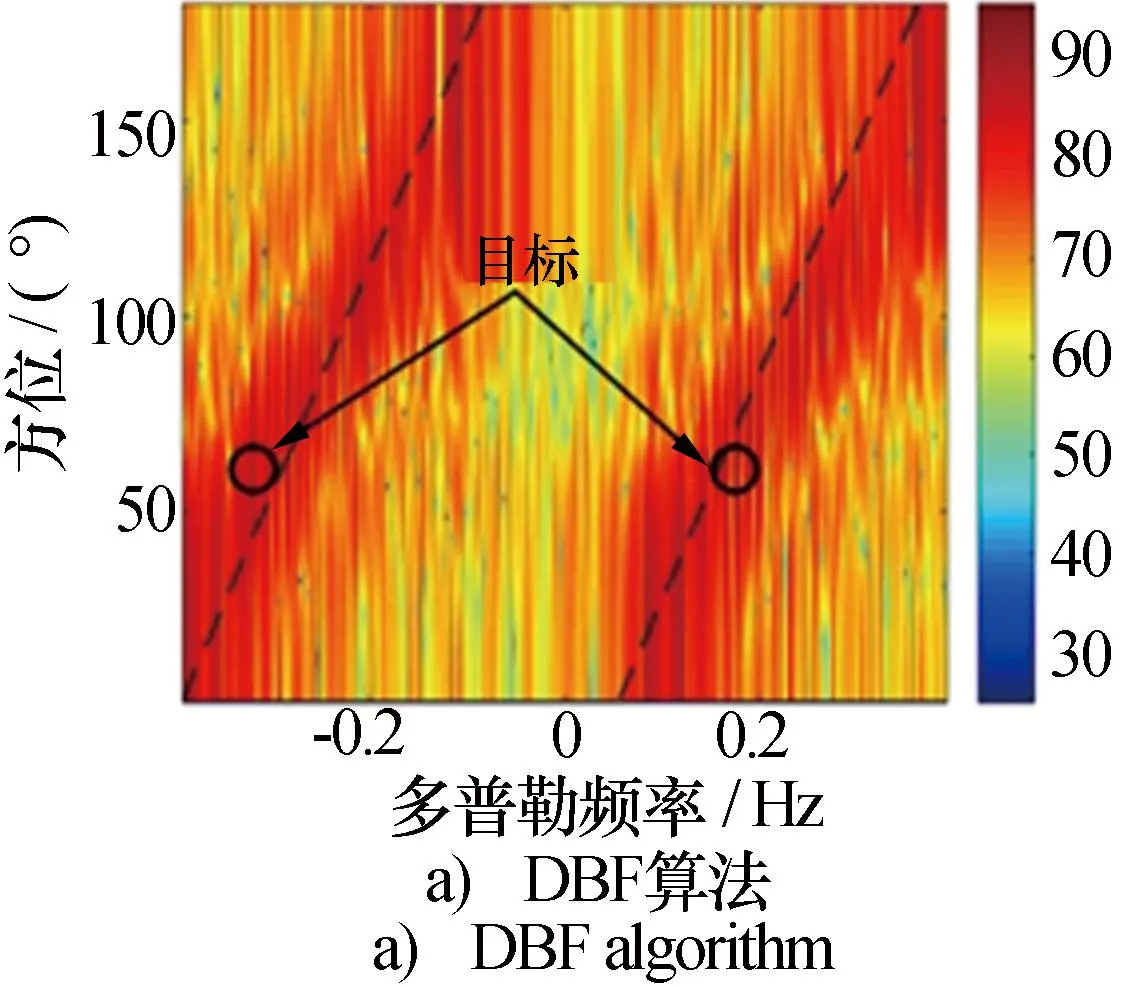
圖4 仿真海雜波抑制結果

圖4a)是DBF算法處理后的結果,可以明顯看到一階海雜波展寬非常嚴重,目標被掩蓋在展寬的一階海雜波之中,該方法對海雜波抑制效果很差;圖4b)是JDL算法的抑制結果,該算法對展寬的一階海雜波有一定的抑制作用,但是仍然有殘留的雜波,不利于后續目標的檢測;圖4c)為UTJDL算法的處理結果,可以看出,大部分海雜波都被濾除,但目標方位、幅值不高,仍有可能受到雜波的干擾;圖4d)為本文提出算法的處理結果,可以看出,本文算法對海雜波有很好的抑制作用,并且艦船目標在AD譜中很容易準確定位。

下面分別從海雜波抑制及目標方位檢測誤差兩方面,進一步考察以上四種算法的性能好壞。圖5為目標所在方位的多普勒截面曲線,從中可見,本文方法對海雜波抑制效果最好,且本文算法的多目標檢測能力最佳,因為目標1和目標2的分辨率都是最高的。圖6為目標1所在頻率的方位截面曲線,目標方位位于60°,從中可見,本文方法測得的目標準確度最高,并且最高幅值不受其他角度的影響,本文算法明顯優于JDL以及UTJDL算法。這主要是因為單快拍MUSIC算法通過預處理提高了角度估計的精度,并且改進的UT算法能夠獲得更均勻的次要數據,使得感興趣距離單元雜波協方差矩陣的估計精度提高。

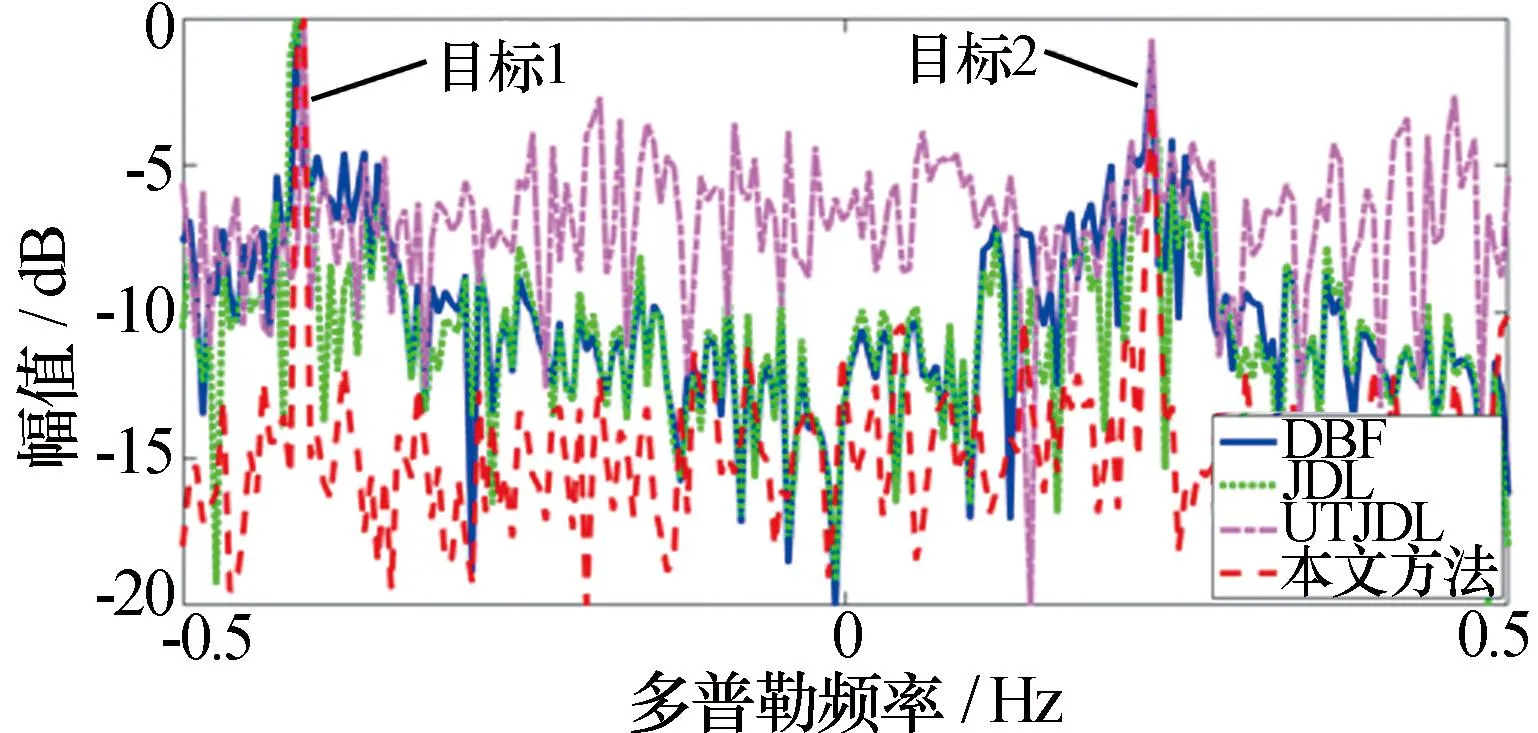
圖5 四種算法海雜波抑制性能對比

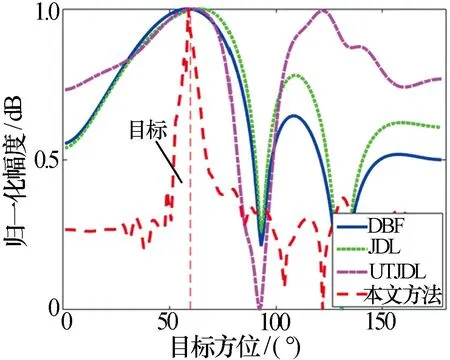
圖6 四種算法目標方位檢測精度對比

表3給出了四種算法經過100次蒙特卡羅實驗后檢測到的目標最大幅值與雜波差的平均值ΔA、輸出SCNR的平均值以及SCNR平均提升量。由表3可知,本文算法SCNR提升量最高,在雜波抑制后目標更容易被檢測到。

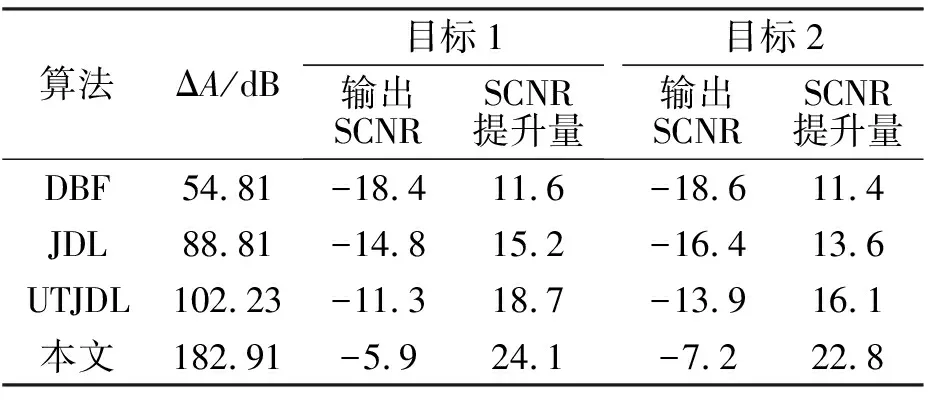
表3 四種算法海雜波抑制性能對比表

2.2 實測海雜波抑制結果

為進一步驗證算法的性能,下面利用中國海洋大學威海移動站于2019年7月20日7時51分測得的海雜波數據進行實測。本文在實測數據中添加兩個距離為40km,角度為60°,頻率分別為-0.1106Hz和0.398 2 Hz的仿真目標,仿真目標的輸入SCNR為-30 dB。圖7為DBF、JDL、UTJDL及本文算法對實測數據的處理結果。由于實測數據受到天線方向圖誤差的影響,無論是目標信號還是海雜波都會被其來向所對應的天線誤差加權[22],因此DBF算法的結果最差,而本文算法AD譜中目標分辨率最高,并且很容易分辨目標所處方位。

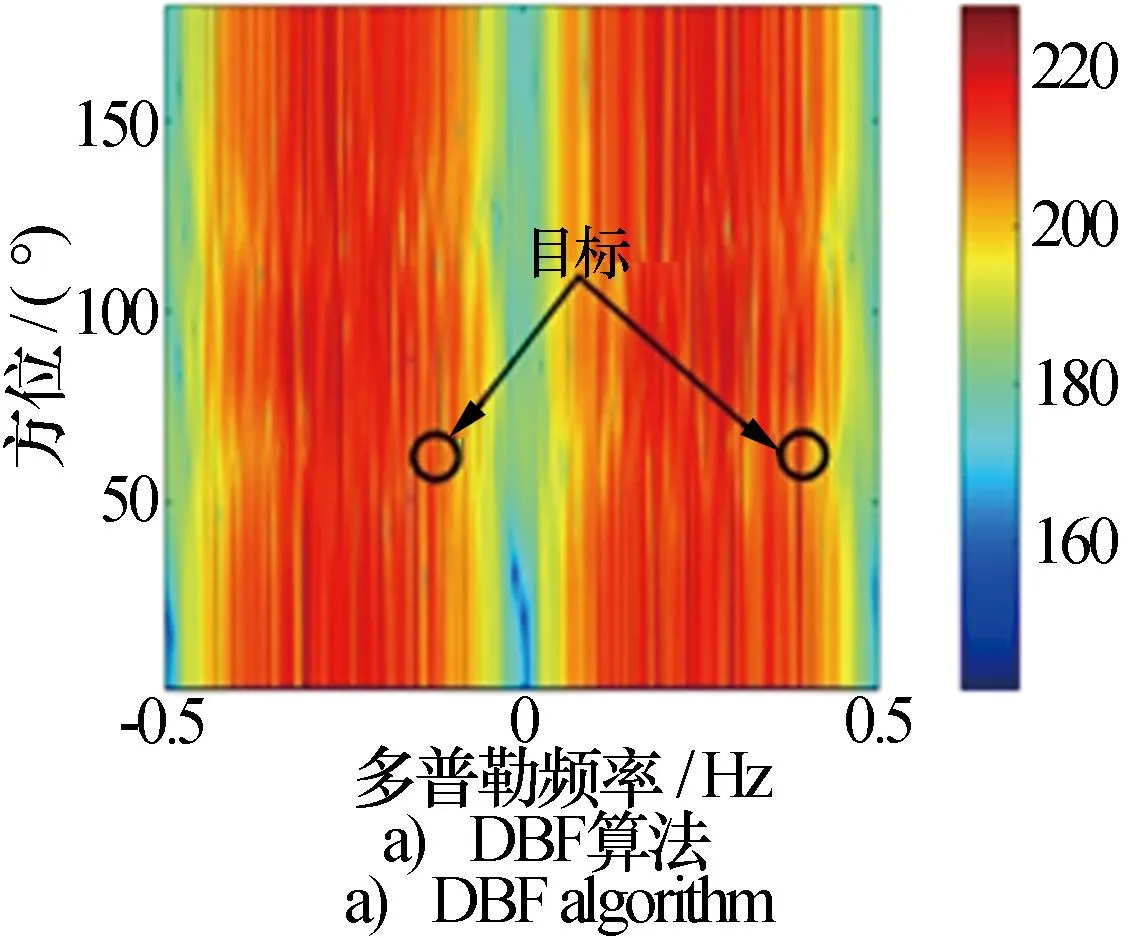
圖7 實測海雜波抑制結果

圖8為實測數據在四種算法抑制后目標所在角度為60°的多普勒截面,可見對于實測數據,本文算法不僅能抑制雜波,還能使目標分辨率最高。圖9為實測數據在四種算法抑制后目標所在頻率的角度估計,相較于傳統算法,本文算法檢測精度最高。

圖8 四種算法對實測海雜波抑制性能對比

圖9 四種算法對實測數據目標方位檢測精度對比

表4展示了實測數據在四種算法處理后的目標幅值與雜波最大差值的平均值以及輸出SCNR的平均值,從中可見,本文算法在實測數據處理時一階海雜波背景被很好地抑制,目標幅值與海雜波最大差值的平均值最大,并且輸出的SCNR最大,海雜波抑制前后SCNR提升量最大。

表4 四種算法對實測海雜波抑制性能對比表

2.3 算法運算量分析

本節將分析改進算法的運算量。假設雷達陣列為均勻線性陣列,陣元數為N,脈沖積累個數為M,距離單元數為r,下面分別從單快拍MUSIC算法及基于改進UT算法的JDL濾波算法兩部分分析運算量。

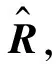
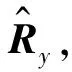
(14)

根據式(14),利用實測數據中的參數取值M=1 024,N=7,ηa=ηb=3,r=23,得到改進算法的總運算量約為1.610 96×1010次浮點運算。因此,本文算法計算量的降低主要在體現在單快拍MUSIC算法的應用上。

3 結束語

針對傳統海雜波抑制算法對非均勻海雜波抑制能力不足以及現有優化方法存在局限性的問題,本文提出了一種單快拍MUSIC與改進UTJDL結合的船載HFSWR海雜波抑制與目標檢測算法。利用單快拍MUSIC可以提高目標角度估計的準確率和處理效率,通過SVD分解可以解決傳統UT算法中非正定矩陣導致的濾波發散問題。利用改進的UT算法可以獲取均勻的估計樣本,解決了傳統JDL算法需要不同距離單元服從獨立同分布的問題。此外,利用不同距離元之間的相關性系數對估計樣本的協方差矩陣進行加權,可以提高協方差矩陣估計的準確性。從仿真數據和實測數據的實驗結果可以看出,與傳統算法相比,本文算法對同角度不同頻率的多目標檢測能力最佳,目標角度、頻率的估計都較為準確,且信雜噪比提升最大。

此外,本文算法不僅適用于船載HFSWR海雜波抑制,還適用于所有均勻訓練樣本有限的情形。本文提出的雜波抑制算法是一種解決非均勻雜波問題的有效方法,對復雜環境下目標和雜波的適應性較強。然而,本文算法無跡變換采用線性變換代替非線性變換,如何找到一種合適的非線性變換是今后的研究重點。另外,由于實測目標距離單元未知,今后研究中可以搭配船舶自動識別系統,先確定目標信息后再進行實測海雜波抑制,這樣能更好地驗證本文算法對未知海雜波的抑制能力。