基于稀疏環境監測點的流動時程重構模型精度研究

戰慶亮,劉 鑫,晁 陽,葛耀君

基于稀疏環境監測點的流動時程重構模型精度研究

戰慶亮1*,劉 鑫1,晁 陽1,葛耀君2

(1.大連海事大學交通運輸工程學院,遼寧 大連 116026；2.同濟大學土木工程學院, 上海 200092)

根據有限數量且稀疏分布的環境流場監測點處的觀測數據,得到更多空間位置處的環境測點的流動時變信息,能夠為大氣監測、水體監測和污染物擴散等問題的控制與研究提供更加豐富的數據.本文研究了物理約束對機器學習流場時程表征模型的精度影響規律,研究了可用測點數以及物理約束權重對重構精度的影響.以低雷諾數方柱大氣繞流為例,開展了基于稀疏環境監測點的數據進行高空間分辨率流場時程重構的精度研究.研究發現當監測點數量增至500時精度不再提高;當監測點數量僅有50時,約束權重為10可得到最優結果.結果表明,通過選擇合適的物理約束影響權重,可以有效彌補可用數據較少的問題,為環境流動問題的數據處理和高分辨率流場重構提供了新的方法與依據.

環境流場時程；稀疏監測點；環境流場重構；物理約束；測點數量

流場是環境科學研究中的重要領域,流場監測的時變信息有助于預測和管理環境中的水文、氣象和污染擴散過程.例如,流場信息有助于明確空氣污染的擴散和傳播規律[1-2],可以幫助研究水污染物的擴散和輸運機制[3-4],也對大氣的時變研究具有重大作用[5-6],能夠更好地理解氣候變化的機制等、為環境保護和資源利用提供科學依據[7-8].當進行空氣質量監測、氣象監測以及水體監測等研究時,通常是在城市、工業區、交通樞紐等地點或者河流湖泊的若干位置布設一些流場測點,例如空氣質量監測站、水體質量監測站等.這些測點通常只能提供局部的流場數據,而無法提供更全面的大范圍流場及污染物的時變信息.為了更好地全面了解城市空氣質量、水體等狀況,需要通過稀疏測點的流場重構其他位置處的信息,對觀測區域內的時變物理信息進行預測和評估.然而,環境中流場的時空變化規律復雜,不僅單個測點的物理量呈現復雜的時變特征,同時不同測點之間的物理量變化規律也各不相同,導致了在僅有少量已知測點的流場信息的情況下很難重構整個流場.

隨著人工智能技術的發展,深度學習逐漸成為復雜流動重構問題研究的新方法[9],例如基于卷積神經網絡(CNN)的重構方法和基于生成對抗網絡(GAN)的流場重構方法.一方面,部分研究通過超分辨率圖像重建[10]、殘差網絡[11-12]、多時間路徑卷積神經網絡[14]等方法進行流場重構,另一部分研究采用生成對抗網絡模型[15-18],通過訓練使得對抗模型能夠對空間和時間的流動數據進行判斷,促使生成模型產生高度準確且具有豐富細節的時變物理量.這些研究的重構思路均是基于模型的圖像特征識別與增強實現的.

然而,上述研究方法中使用的數據通常是實驗獲取或模擬的流場快照數據,在實際環境流場問題中難以獲得大范圍的流場快照數據.流場測點處的時程數據是目前環境實驗能夠獲取的主要數據類型,但是目前針對流動時程的深度學習研究較少.如文獻[19]提出了針對流場時程數據的流動表征和流動特征識別的方法[20-21].此外,還進行了對流場時程特征進行提取的模型研究[22-23],為深度學習方法在流場時程數據的分析和重構應用方面提供了可行的解決方案.然而,在訓練樣本數據有限的情況下,這些方法在通過數據驅動的模型訓練方式獲取準確結果方面存在一定的困難.

為了克服純數據驅動的流場研究難點,借鑒Raissi等[24]提出的求解方程與參數反演方法[25],文獻[26]提出了考慮物理方程約束的流場表征的機器學習方法,初步結果表明能夠在已知測點數據較少的情況下提高模型的準確性.該方法非常適合用于環境測點的流場重構研究,然而環境測點個數對精度的影響、物理約束強度對模型精度的影響機制并不明確.因此,本研究進一步討論不同數量已知監測點以及物理信息在損失函數中的占比對稀疏環境監測點的時程重構模型精度問題.

1 問題與方法

1.1 流動問題及模擬

本文以環境流動的基本輸運量開展研究,主要針對速度場和壓力場進行求解與重構.其他物理量(例如溫度場、密度場以及污染物濃度等)的輸運方程可基于所求速度場進行計算,這些物理量方程求解時強非線性對流項的速度場是已知的,因此求解較容易,其重構方法與本文所述無本質區別,這里選擇低雷諾數下的方柱繞流問題為例開展具體討論.具體的,以環境流動中廣泛存在的方柱繞流場為例,討論深度學習模型的物理約束機理.

計算域如圖1a所示,雷諾數= 100.其中方柱的邊長為,方柱周圍矩形區域內使用較密的網格,距離方柱較遠的區域使用較稀疏的網格.入口邊界條件設置速度入口,右側邊界為壓力出口,上下邊界為對稱邊界條件,方柱壁面設置為無滑移邊界.

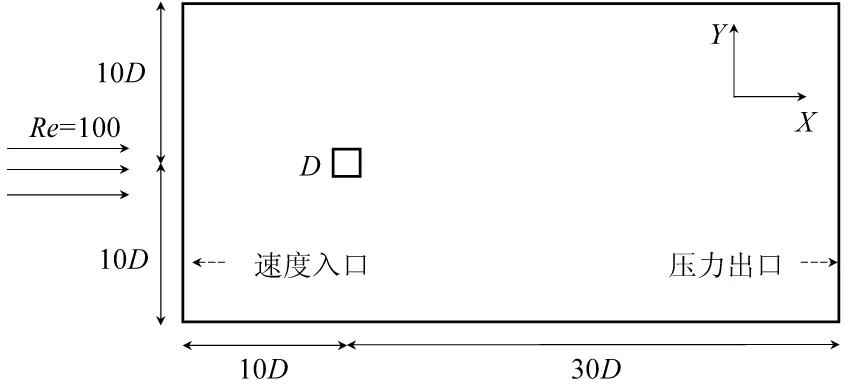
(a) 計算域

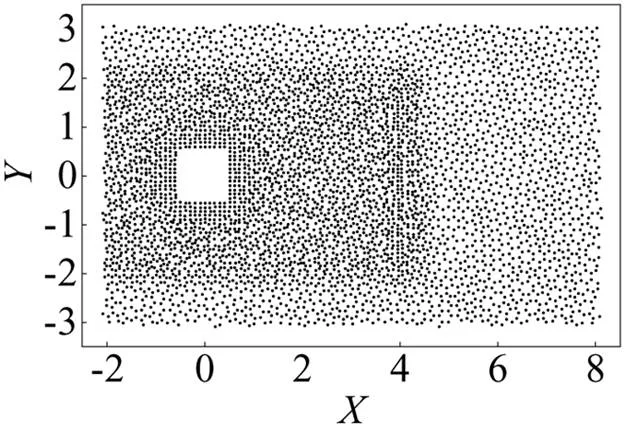
(b) 測點

圖1 流場計算域和測點布置

Fig.1 Sketch of computational domain and sampling points

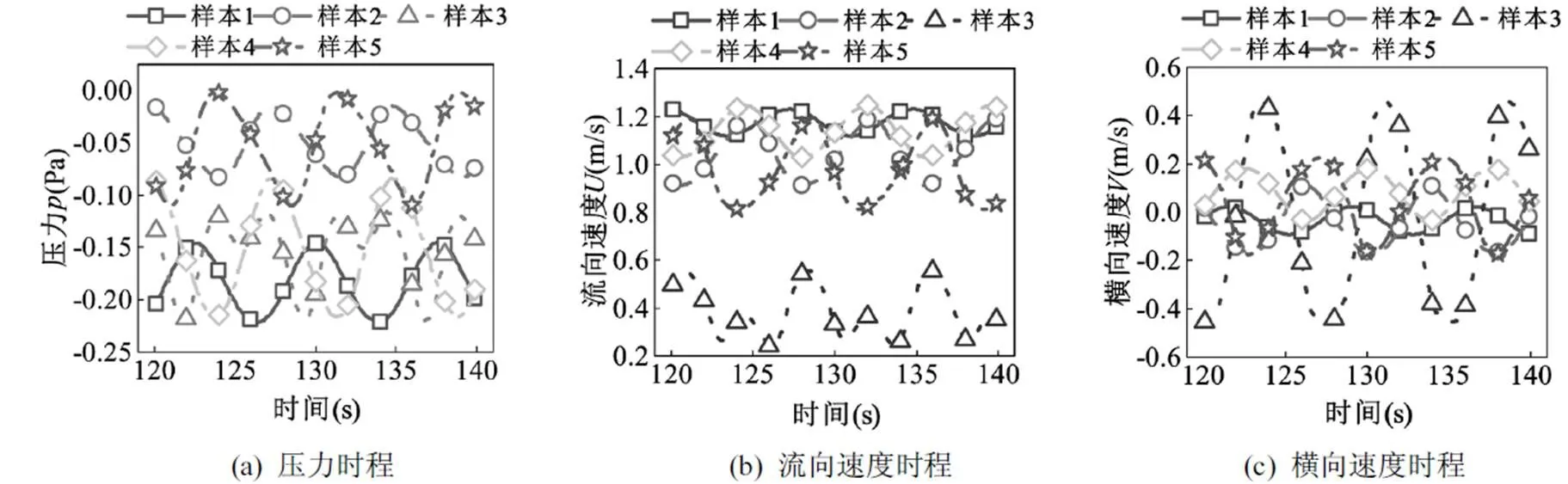
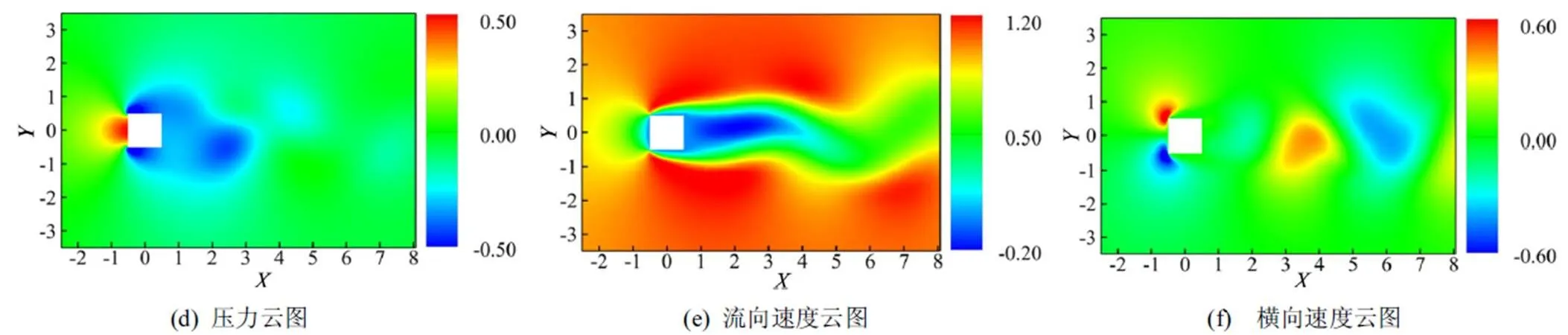
圖2 測點時程曲線與瞬態流場云圖

在方柱周圍和下游區域布置了多個流場監測點,用于記錄環境流場中的物理量隨時間的變化,如環境中的溫度與風速變化.這些監測點涵蓋了方柱周圍的7000個位置,如圖1b所示.使用zFlower軟件計算了每個監測點處的物理量時程,并得到了不同位置的物理量隨時間的變化曲線.此外,選擇特定時刻的瞬時值按照測點位置排列,可以得到流動瞬態云圖,如圖2所示.

環境問題研究中的流動監測范圍通常很大,無法布置如本算例所示的如此密集的測點,因此,探索如何利用少量測點的時程數據對模型進行訓練以提高準確度,對環境流場的重構和預測具有重要的研究價值.

1.2 物理信息約束的重構模型

本文采用深度學習網絡模型,通過對已知測點樣本進行訓練,實現對計算域中其他測點處物理量時程的預測.所采用的網絡模型結構如圖3所示[26],其輸入層包括測點坐標和時程信息,輸出層包括壓力、流向速度和橫向速度的時程.

模型的基本計算流程如下:(1)通過深度學習網絡模型建立測點坐標與壓力、流向速度和橫向速度時程之間的映射關系模型結構;(2)并通過已知測點的坐標和時程對網絡模型的權重進行訓練;(3)通過將輸入層與神經網絡(NN)輸出的時程與Navier- Stokes方程相結合,構建了物理約束(PC)的損失項,并通過模型訓練同時降低時程誤差和方程誤差,完成模型的訓練;(4)在模型中輸入待預測點的坐標,即可得到該點處的流場時程信息,從而實現大范圍空間的流場重構.

其中,物理約束的損失項表達式如下所示:

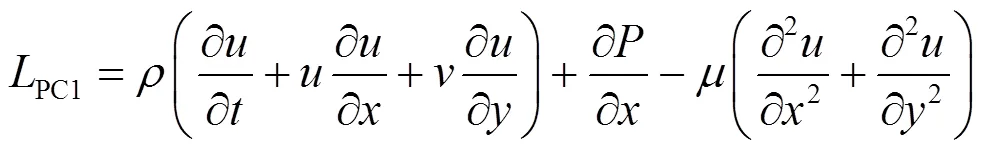
式中:(,)代表計算域中測點的空間坐標;表示壓力;和分別表示流向速度和橫向速度;PC代表物理約束方程損失項;NN表示神經網絡的損失,它衡量了模型輸出值與已知測點真實時程之間的差異,可以看作是訓練過程中模型對已知測點的擬合誤差.加入物理方程約束后,模型的總損失函數為:

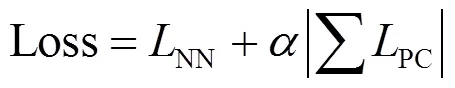
其中參數為約束強度系數(constrain factor),表示物理約束條件與神經網絡對已知樣本訓練之間損失的比例關系,通過控制大小變化來檢驗模型.

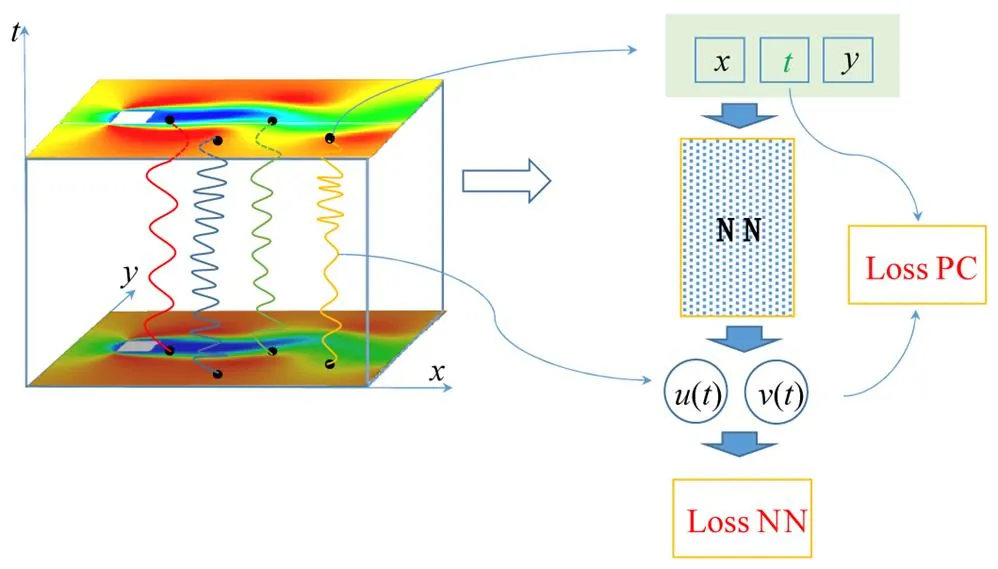
圖3 人工神經網絡模型的原理[26]

2 結果與分析

本部分主要包含兩部分研究,分別為不同數量已知監測點和不同物理約束強度系數對重構模型的精度影響.

2.1 已知監測點數量的影響

考慮到訓練集大小會對模型結果的精度產生不同影響,分別訓練不同數量的監測點時程數據,從7000個監測點中隨機選取個樣本點作為訓練集,在模型訓練過程中,僅需要該個點的數據信息.訓練集數量范圍從=50增大到=5000,如圖4所示為樣本測點布置情況,圖中紅色點為用于訓練集的樣本點,綠色測點不參與模型的訓練.

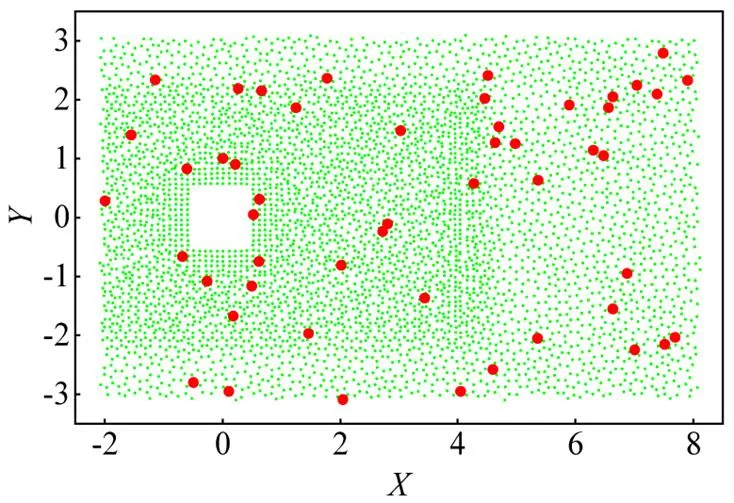
(a)=50 (b)=100

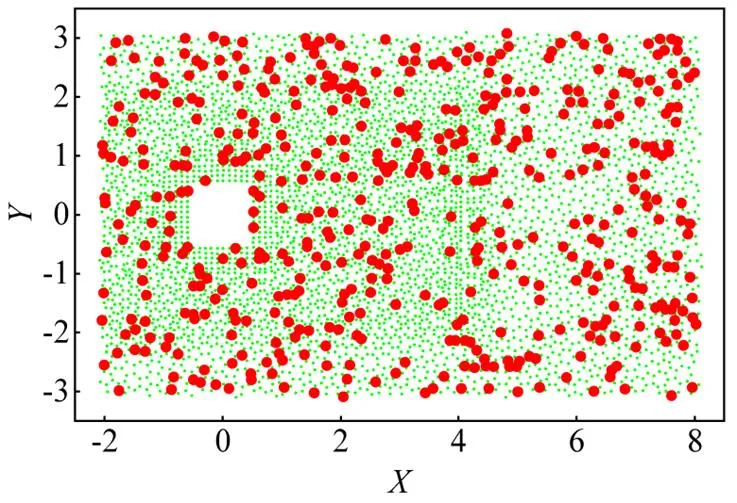
(c)=500 (d)=3000

圖4 隨機選擇的訓練測點位置

Fig.4 Randomly selected measurement points locations for training

首先不對模型施加方程約束,此時為純數據驅動模型,即物理約束強度=0,模型的損失為已知的監測時程與模型輸出時程的均方誤差,不同樣本量訓練總損失情況如圖5所示.計算中,若損失趨于平穩則提前終止訓練,每條損失曲線最終損失值均達到10-4數量級,且訓練集數量越大需要的迭代次數(epoch)越少.

參考文獻[26]中表示預測誤差的計算方法,把不同坐標點的誤差繪制成無量綱化的誤差散點圖.各算例采用除訓練集外相同位置的測點作為預測集,不同誤差以不同顏色來表示,若誤差值小于5%用綠色表示,5%～10%之間用藍色表示,10%～20%之間用黃色表示,20%～50%之間用粉紅色表示,大于50%用紅色表示.

圖6所示為不同數量測點進行訓練的模型預測結果,包含流向速度與橫向速度的誤差散點圖以及對應的高分辨率瞬態云圖.

結果表明,隨著測點數量的增加,誤差散點圖精度最高的綠色區域范圍不斷擴大,誤差最大的紅色區域減小,且對應的預測云圖逐漸接近真實的云圖結果.

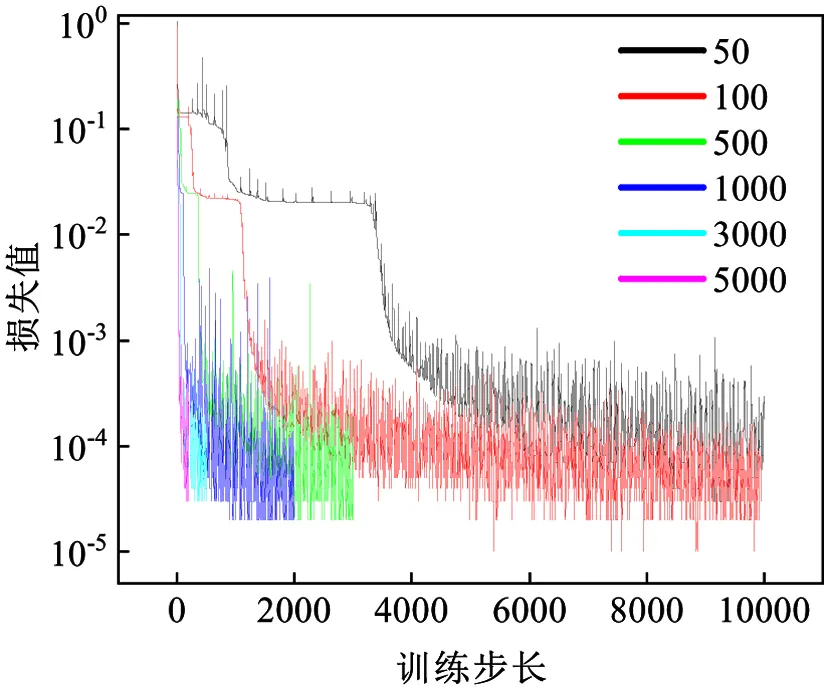
圖5 模型訓練總損失

圖7為上述各誤差散點圖在空間維度上的均值,誤差均值曲線呈下降趨勢,且在測點數量= 500時逐漸趨于平緩,說明模型精度隨測點數量的增加而增大.實際的環境流動問題監測時往往難以直接獲得更多測點的數據,因此要研究物理約束強度的影響.

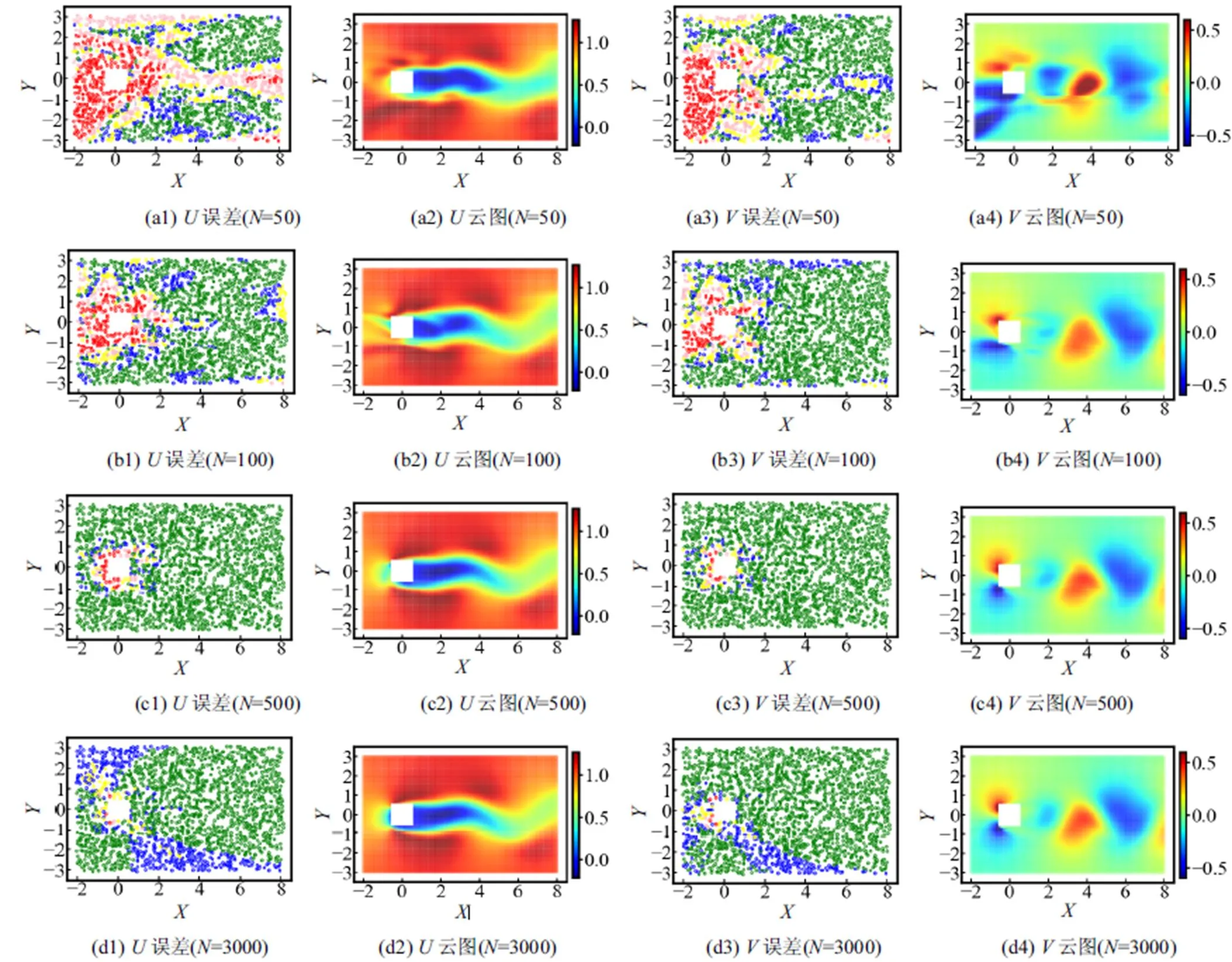
圖6 誤差分布與重構的瞬態云圖

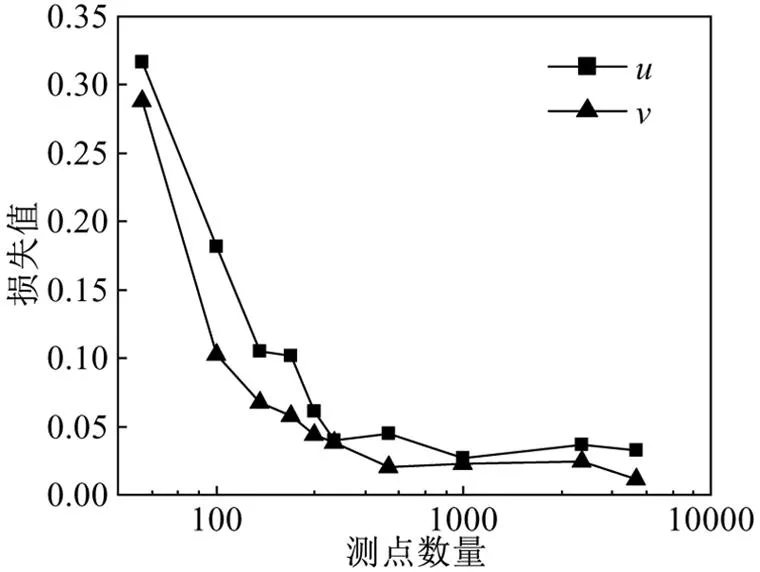
圖7 誤差隨測點數量變化

2.2 物理信息的損失占比影響

進一步研究不同的物理信息約束損失占比對于模型擬合效果的影響.本文選取不同的范圍為[10-9, 103],以50個樣本點作為稀疏的已知環境流動監測信息,重構整個流動的預測模型.

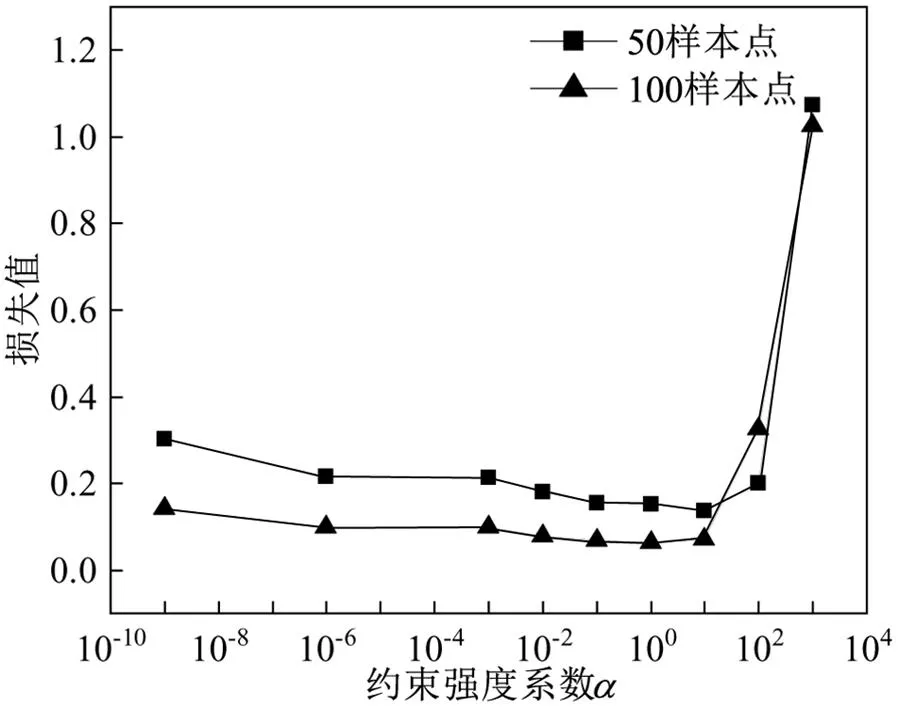
模型訓練后的測點時程誤差均值如圖8所示,圖8a為不同下的流向速度和橫向速度的誤差均值,圖8b為壓力誤差.結果表明=50時兩幅圖中均在=10處誤差達到最小值,速度時程的精度提高了2倍,壓力時程的精度提高了20倍;=100時在=1處得到最小值,速度時程的精度提高了2倍,同時壓力時程的精度提高了50倍;不施加物理約束即=10-9時,模型無法擬合壓力時程數據導致壓力誤差過大,方程約束在損失函數中占比過大即=103時,重構效果不理想導致速度誤差過大.

使用不同的約束強度系數對模型進行訓練并保存模型,預測結果如圖9所示.當10-9時可看作不施加物理約束,得到的結果與數據驅動結果相同,且觀察到橫向速度云圖誤差極大;當增大至10-1時初步得到擬合較好的云圖,但流場上游區域誤差較大;當為1和10時取得了最優的云圖結果,其中為10的誤差散點圖精度最高;繼續增大到102時預測效果不理想,達到103時方程項占比過大導致模型訓練失敗.

(a) 速度誤差均值 (b) 壓力誤差均值

圖8 誤差隨參數α變化

Fig.8 Model error with respect to α

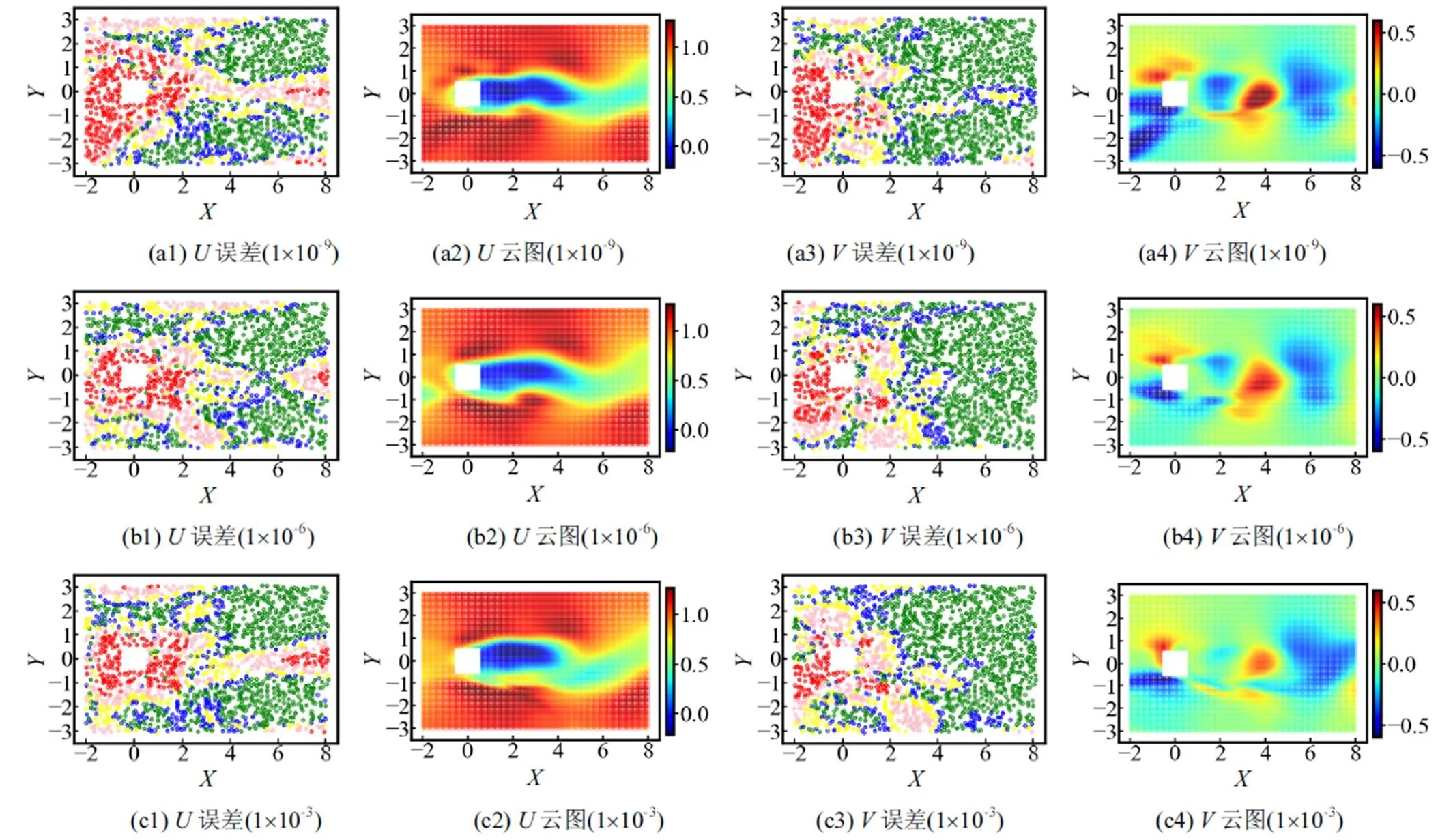
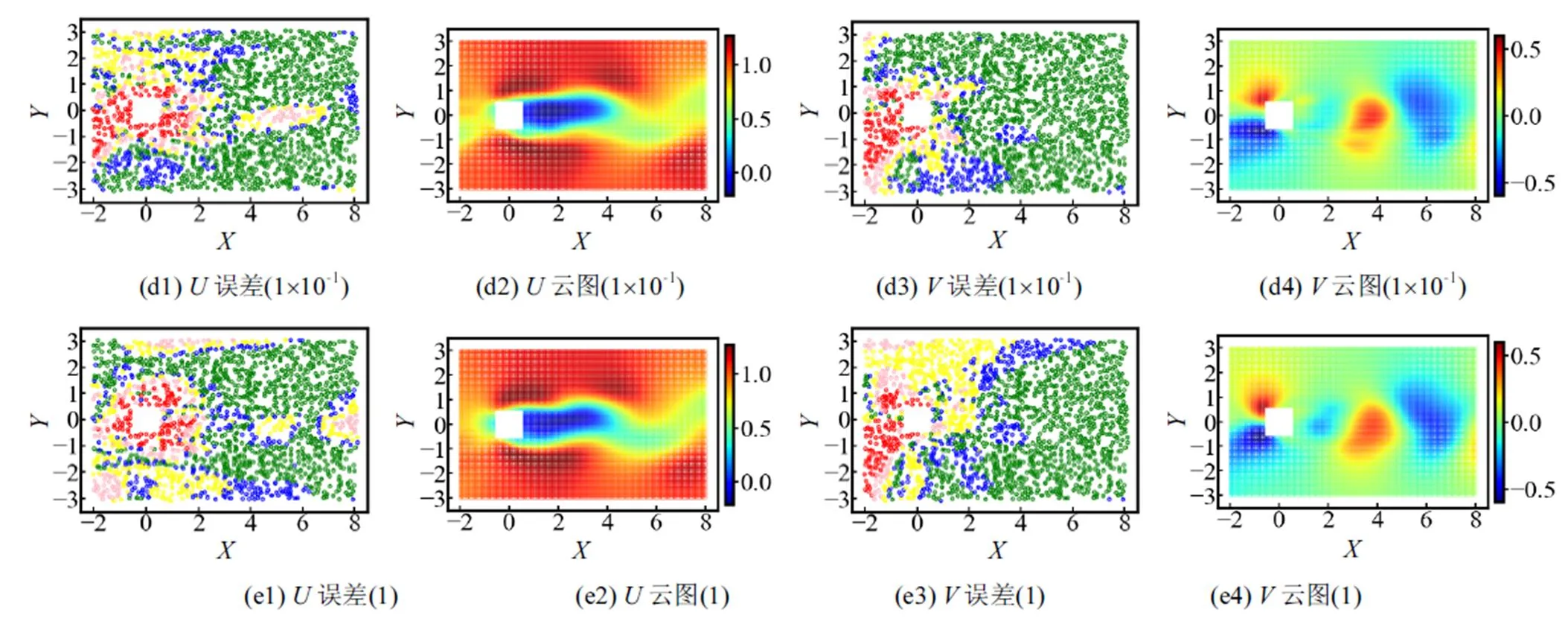
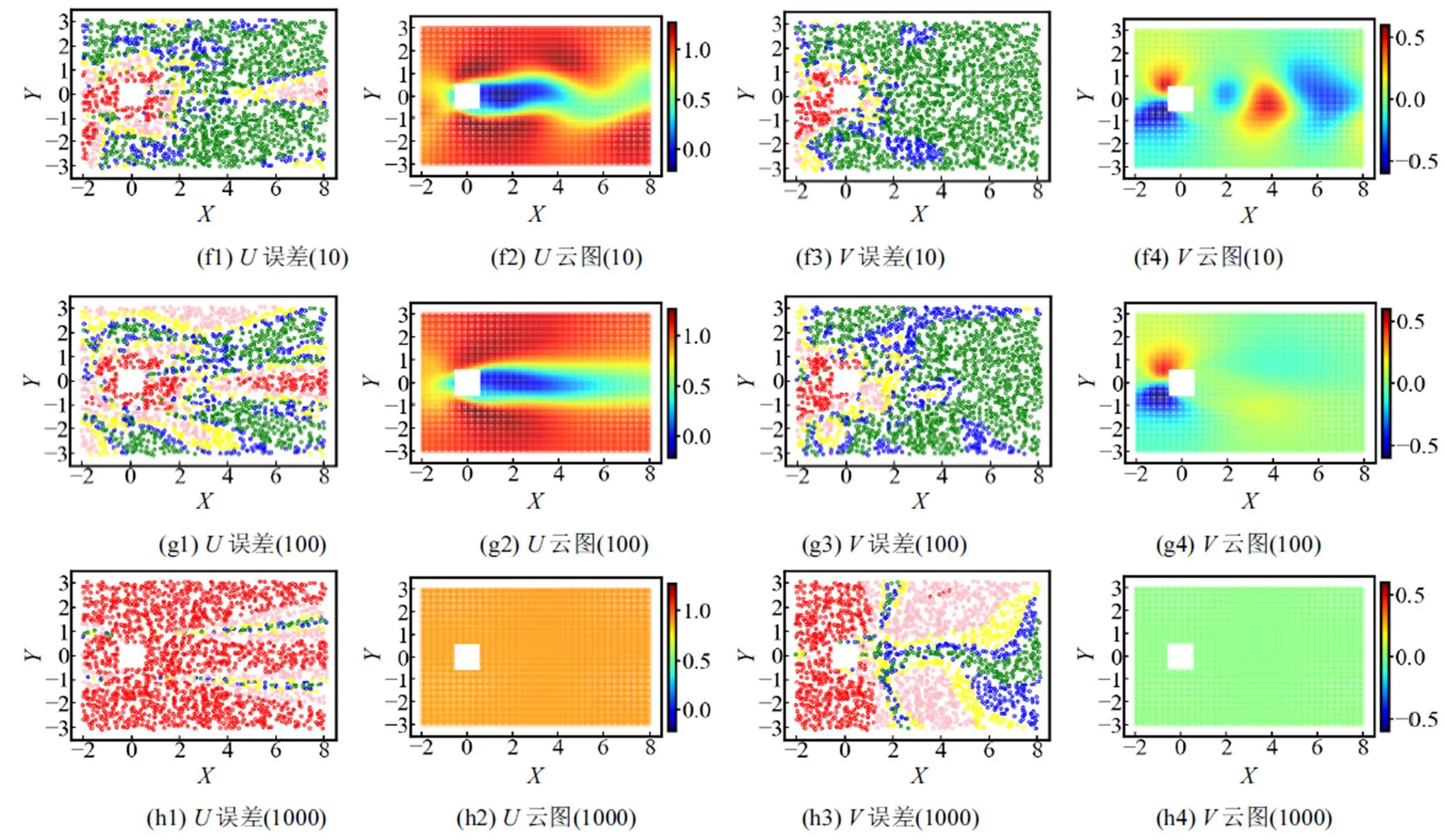
圖9 速度誤差分布與重構的瞬態云圖

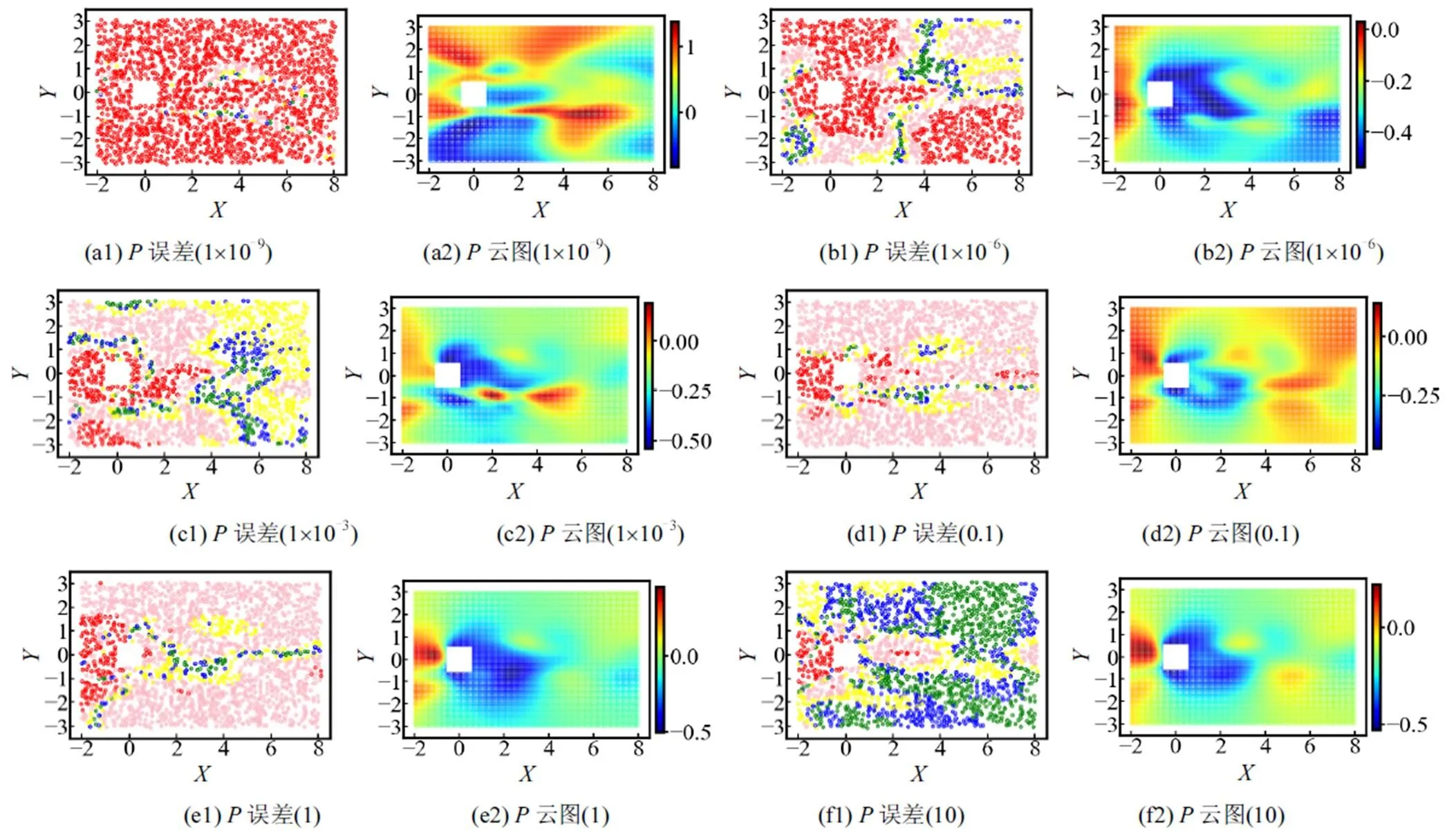
圖10 壓力誤差分布與重構的瞬態云圖

同時模型得到了壓力的預測結果,如圖10所示.在模型訓練時,壓力時程數據并不作為已知條件,是不參與模型訓練的.壓力時程直接由模型輸出并通過方程約束精度,故在稀疏數據情況下較難擬合高分辨率壓力云圖.圖中表明當=10時可得到較理想的云圖結果,且誤差散點圖綠色區域顯著擴大.綜上可說明物理信息的損失占比對模型結果的影響不容忽視,在為某一數值范圍的情況下模型可獲得最優解.

3 結論

3.1 隨著訓練集監測點數量的增加,模型的預測精度逐步提升,基于數據驅動的模型結果在測點數量=500時誤差逐漸趨于穩定.

3.2 物理方程約束項在模型損失函數中的占比較重要,在樣本數據稀疏的情況下可提高精度.測點數量=50時,物理方程約束項的占比=10處誤差得到最小值;測點數量=100時,=1處誤差得到最小值.

3.3 基于時程的深度神經網絡模型可預測未知測點處的時程,后續應進一步探索復雜流動的模型精度,并實現基于實測稀疏的環境流動監測數據的高空間分辨率流場重構.

[1] 周 琪,于 洋,劉苗苗,等.基于機器學習和非參數估計的PM2.5風險評估 [J]. 中國環境科學, 2022,42(8):3554-3560.

Zhou Q, Yu Y, Liu M M, et al. Risk assessment of PM2.5pollution based on machine learning and nonparametric estimation [J]. China Environmental Science, 2022,42(8):3554-3560.

[2] 周恒左,陳恒蕤,廖 鵬,等.蘭州市CMAQ近地面臭氧模擬結果的訂正方法——基于機器學習方法 [J]. 中國環境科學, 2022,42(12): 5472-5483.

Zhou H Z, Chen H R, Liao P, et al. A revised approach to CMAQ near-surface ozone modelling results in Lanzhou-Based on machine learning methods [J]. China Environmental Science, 2022,42(12): 5472-5483.

[3] 嵇曉燕,姚志鵬,楊 凱,等.基于MSLSTM-DA模型的水質自動監測異常數據報警 [J]. 中國環境科學, 2022,42(4):1877-1883.

Ji X Y, Yao Z P, Yang K, et al. Water quality alert with automatic monitoring data based on MSLSTM-DA model [J]. China Environmental Science, 2022,42(4):1877-1883.

[4] 任永琴,金柱成,俞真元,等.基于雙向門控循環單元的地表水氨氮預測 [J]. 中國環境科學, 2022,42(2):672-679.

Ren Y Q, Kim J S, Yu J W, et al. Ammonia nitrogen prediction in surface water based on bidirectional gated recurrent unit [J]. China Environmental Science, 2022,42(2):672-679.

[5] 張寒博,楊 驥,荊文龍,等.多種特征因子結合GBDT的降水數據降尺度方法研究 [J]. 中國環境科學, 2023,43(4):1867-1882.

Zhang H B, Yang J, Jing W L, et al. Downscaling method of precipitation data based on GBDT combined with multiple eigenfactors [J]. China Environmental Science, 2023,43(4):1867- 1882.

[6] 李靜波,張 瑩,蓋榮麗.基于機器學習的星載短波紅外CO2柱濃度估算 [J]. 中國環境科學, 2023,43(4):1499-1509.

Li J B, Zhang Y, Gai R L. Estimation of the column concentration of carbon dioxide using spaceborne shortwave infrared spectrometer [J]. China Environmental Science, 2023,43(4):1499-1509.

[7] 葛淵博,盧文喜,白玉堃,等.基于SSA-BP與SSA的地下水污染源反演識別 [J]. 中國環境科學, 2022,42(11):5179-5187.

Ge Y B, Lu W X, Bai Y K, et al. Inversion and identification of groundwater pollution sources based on SSA-BP and SSA [J]. China Environmental Science, 2022,42(11):5179-5187.

[8] 潘紫東,盧文喜,范 越,等.基于模擬-優化方法的地下水污染源溯源辨識 [J]. 中國環境科學, 2020,40(4):1698-1705.

Pan Z D, Lu W X, Fan Y, et al. Inverse Identification of groundwater pollution source based on simulation-optimization approach [J]. China Environmental Science, 2020,40(4):1698-1705.

[9] 張偉偉,竇家慶,劉溢浪.智能賦能流體力學展望 [J]. 航空學報, 2021,42(4):524689.

Zhang W W, Kou J Q, Liu Y L. Prospect of artificial intelligence empowered fluid mechanics [J]. Acta Aeronautica et Astronautica Sinica, 2021,42(4):524689.

[10] Zhou L, Lu X, Yang L. A local structure adaptive super-resolution reconstruction method based on BTV regularization [J]. Multimedia Tools and Applications, 2014,71(3):1879-1892.

[11] Lim B, Son S, Kim H, et al. Enhanced deep residual networks for single image super-resolution [A]//O’Conner L.2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW) [C]. Piscataway: IEEE, 2017:1132-1140.

[12] Tai Y, Yang J, Liu X. Image super-resolution via deep recursive residual network [A]//O’Conner L.2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) [C]. Piscataway: IEEE, 2017:2790-2798.

[13] Lai W S, Huang J B, Ahuja N, et al. Deep laplacian pyramid networks for fast and accurate super-resolution [A]//O’Conner L.2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) [C]. Piscataway: IEEE, 2017:5835-5843.

[14] Liu B, Tang J, Huang H, et al. Deep learning methods for super-resolution reconstruction of turbulent flows [J]. Physics of Fluids, 2020,32(2):25105.

[15] Xie Y, Franz E, Chu M, et al. Tempo GAN: A temporally coherent, volumetric GAN for super-resolution fluid flow [J]. ACM Trans. Graph., 2018,37(4):1-15.

[16] Xu W, Luo W, Wang Y, et al. Data-driven three-dimensional super-resolution imaging of a turbulent jet flame using a generative adversarial network [J]. Applied Optics, 2020,59(19):5729-5736.

[17] Lee J, Lee S, You D. Deep learning approach in multi-scale prediction of turbulent mixing-layer [J]. arXiv: Computational Physics, 2018.doi:10.48550/arXiv.1809.07021.

[18] Lin J, Lensink K, Haber E. Fluid flow mass transport for generative networks [A]//RUSH A, TECH C.ICLR 2020 Conference Blind Submission. [C]. Addis Ababa, Ethiopia: Open Review. net, 2020: 1-10.

[19] 戰慶亮,白春錦,葛耀君.基于時程深度學習的復雜流場流動特性表征方法 [J]. 物理學報, 2022,71(22):224701.

Zhan Q L, Bai C J, Ge Y J. Deep learning representation of flow time history for complex flow field [J]. Acta Physica Sinica, 2022,71 (22):224701.

[20] 戰慶亮,白春錦,葛耀君.基于時程深度學習的流場特征分析方法 [J]. 力學學報, 2022,54(3):822-828.

Zhan Q L, Bai C J, Ge Y J. Fluid feature analysis based on time history deep learning [J]. Chinese Journal of Theoretical and Applied Mechanics, 2022,54(3):822-828.

[21] 戰慶亮,白春錦,張 寧,等.基于時程卷積自編碼的機翼繞流特征識別方法 [J]. 航空學報, 2022,43(11):526531.

Zhan Q L, Bai C J, Zhang N et al. Feature extraction method of flow around airfoil based on time-history convolutional autoencoder [J]. Acta Aeronautica et Astronautica Sinica, 2022,43(11):526531.

[22] 戰慶亮,葛耀君,白春錦.基于深度學習的流場時程特征提取模型研究 [J]. 物理學報, 2022,71(7):074701.

Zhan Q L, Bai C J, Ge Y J. Flow feature extraction models based on deep learning [J]. Acta Physica Sinica, 2022,71(7):074701.

[23] 戰慶亮,葛耀君,白春錦.流場特征識別的無量綱時程深度學習方法 [J]. 工程力學, 2023,40(2):17-24.

Zhan Q L, Bai C J, Ge Y J.Deep learning method for flow feature recognition based on dimensionless time history [J]. Engineering Mechanics, 2023,40(2):17-24.

[24] Raissi M, Karniadakis G E. Hidden physics models: Machine learning of nonlinear partial differential equations [J]. Journal of Computational Physics, 2018,357:125-141.

[25] Raissi M, Perdikaris P, Karniadakis G E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations [J]. Journal of Computational Physics, 2019,378:686-707.

[26] 戰慶亮,劉 鑫,白春錦,等.考慮物理方程約束的機器學習流場時程表征方法 [J]. 工程力學, 2023.doi:10.6052/j.issn.1000-4750.2022. 12.1067.

Zhan Q L, Liu X, Bai C J, et al. Physical constrained flow representation model using machine learning for flow time history [J]. Engineering Mechanics [J]. Engineering Mechanics, 2023.doi:10. 6052/j.issn.1000-4750.2022.12.1067.

Accuracy of environmental flows time history reconstruction model based on sparse observation.

ZHAN Qing-liang1*, LIU Xin1, CHAO Yang1, GE Yao-jun2

(1.College of Transportation Engineering, Dalian Maritime University, Dalian 116026, China；2.College of Civil Engineering, Tongji University, Shanghai 200092, China)., 2023,43(12)：6592～6600

Obtaining more environmental flow data at more monitoring sites based on limited and sparse available flow monitoring points can provide data for the study of atmospheric monitoring, water monitoring and pollutant dispersion issues. In this study, the influence of physical constraints on the accuracy of the machine learning flow field time history representation model was investigated, and the results of different available measurement points and physical constraint influence weights were compared. The environmental flow around a low Reynolds number square column was tested as an example. Results show that when the number of monitoring points was increased to 500, the accuracy did not improve. When the number of monitoring points was reduced to only 50, the error was minimised when the physical constraint weights were set to 10. The results indicate that the problem of less available data can be effectively compensated by choosing appropriate physical constraint influence weights. Providing a new method and basis for data processing and high-resolution flow field reconstruction for environmental flow problems.

environmental flow time history；sparse observation data；environmental flow reconstruction；physical constrain；number of monitoring points

X83

A

1000-6923(2023)12-6592-09

戰慶亮,劉 鑫,晁 陽,等.基于稀疏環境監測點的流動時程重構模型精度研究 [J]. 中國環境科學, 2023,43(12):6592-6600.

Zhan Q L, Liu X, Chao Y, et al. Accuracy of environmental flows time history reconstruction model based on sparse observation [J]. China Environmental Science, 2023,43(12):6592-6600.

2023-04-30

橋梁結構抗風技術交通行業重點實驗室(上海)開放課題(KLWRTBMC21-02);大連海事大學博聯科研基金資助項目(3132023619);國家自然科學基金資助項目(51978527);遼寧教育廳研究計劃項目(LJKZ0052)

* 責任作者, 講師, zhanqingliang@163.com

戰慶亮(1987-),男,遼寧大連人,講師,博士,主要從事環境流體力學研究.發表論文30余篇.zhanqingliang@163.com.