一種基于逆冪核主成分的維度約減方法
張紅艷
(貴州民族大學數(shù)據(jù)科學與信息工程學院,貴陽 550025)
0 引言
隨著科技的進步和計算能力的提高,越來越多的數(shù)據(jù)呈現(xiàn)出高維特點,高維數(shù)據(jù)不僅包含大量的冗余信息,而且處理起來十分耗時。不斷增加的數(shù)據(jù)維度,更會導致所謂的“維數(shù)災難”(dimensionality curse)[1]問題。通過維度約減能有效減少數(shù)據(jù)特征的數(shù)量,提高計算效率。目前,維度約減被廣泛應用于機器學習[2]、數(shù)據(jù)分析、數(shù)據(jù)可視化、自然語言處理[3]和圖像處理[4]等領域。
維度約減可分為線性維度約減和非線性維度約減兩種方法。線性維度約減是指通過線性變換將高維數(shù)據(jù)映射到低維空間中,從而減少數(shù)據(jù)的維度,同時盡可能地保留原始數(shù)據(jù)的關鍵特征。它的典型代表為主成分分析法(principal component analysis,PCA)[5]。PCA 擅長處理線性可分的數(shù)據(jù),當數(shù)據(jù)不可分,或存在缺失、異常等情況時,若仍采用線性維度約減,則數(shù)據(jù)將丟失原本的結構。因此,Sch?lkopf 等[6]提出基于核技巧的主成分分析法(kernel principal component analysis,KPCA)。與傳統(tǒng)PCA 不同,KPCA 可以通過非線性變換將數(shù)據(jù)映射到高維空間中,并在該空間中執(zhí)行PCA,以獲取更有效地捕獲數(shù)據(jù)特征的主成分。
KPCA 通過使用核函數(shù)計算原始數(shù)據(jù)點和高維空間中的映射點之間的相似度來獲得高維空間中的內積矩陣或距離矩陣,然后對矩陣進行分解以獲得主成分和其相關的投影系數(shù)。由于核函數(shù)的能力,它可以處理高維、非線性和具有任意核心密度的數(shù)據(jù)集。核主成分分析的核心之處在于核函數(shù)的選擇[7-8]。因此,構造了一個新的逆冪核函數(shù),并用該核函數(shù)對高維數(shù)據(jù)進行維度約減。通過在四個高維數(shù)據(jù)集上的實驗分析,對比高斯徑向基核、多項式核、全變量情況,逆冪核函數(shù)的維度約減效果相對更優(yōu)。
1 核主成分分析
核主成分分析法是一種非線性的數(shù)據(jù)分析方法,其主要思想是:通過引入非線性變換Φ,將數(shù)據(jù)由輸入空間Rm映射到高維特征空間F,然后在特征空間F中利用PCA 方法進行數(shù)據(jù)分析和處理。
設樣本集X={χ1,χ2,χ3,…,χN}∈Rm通過非線性變換Φ 將樣本點χi映射在特征空間F中是Φ(χi),i= 1,2,…,N,將之中心化后,即轉換為
可得F空間中的協(xié)方差矩陣Σ為
根據(jù)
求Σ的特征值λ和特征向量ν。由式(2)知,計算Σ需知道Φ(χi)和Φ(χj),而Φ又是未知的。但所有的特征向量ν均可以表示為Φ(χ1),Φ(χ2),…,Φ(χN)的線性張成,即
因此,可得
將式(2)、(4)代入式(5),令
得
其中:K為N×N核矩陣,nλi是K的特征值,α=α1,α2,…,αN是對應的特征向量。按一定的標準取前m(m<N)個特征值和對應的標準化后特征向量α1,α2,…,αm。此時特征空間F中樣本點Φ(χi)在ν上的投影為
在進行維度約減時,怎么確定降維后應保留的屬性維度d,主要取決于數(shù)據(jù)集和核函數(shù),不同的數(shù)據(jù)集和核函數(shù)分類預測精度不一樣。一般采用包裹式學習算法,即屬性維度d的取值與后續(xù)機器學習分類算法的表現(xiàn)性能聯(lián)系在一起,取得的屬性維度d應使后續(xù)分類算法的分類精度更優(yōu)[7]。
2 核函數(shù)
2.1 常見核函數(shù)
由低維空間向高維空間映射帶來的困難就是計算復雜度的增加,而核函數(shù)正好巧妙地解決了這個問題。這一過程是通過用核函數(shù)K(χi,χj)=<Φ(χi)Φ(χj)>代替Wolfe對偶問題中χi和χj的點積來實現(xiàn)的。常用的核函數(shù)如下:
(1)多項式核:
(2)高斯徑向基核:
其中,r,q,γ是核函數(shù)參數(shù)。r是平移參數(shù),r≥0;q是多項式階數(shù),常見取值范圍為(1,10);γ是一個超參數(shù),控制數(shù)據(jù)點在高維空間中的分布情況,常見取值范圍為(10-3,103)。
2.2 逆冪核函數(shù)
核主成分分析法的關鍵是核函數(shù)的選擇是否恰當,不同的數(shù)據(jù)利用不同的核函數(shù)能有效提高維度約減效果,并能有效提高后續(xù)機器學習分類算法的預測性能,依據(jù)核函數(shù)的構造原理,本節(jié)構造新的核函數(shù),稱其為逆冪核函數(shù)。
定義1[9]稱二元函數(shù):X× Χ →R 是正定的,如果它是對稱的,即K(χ,χ')= K(χ,χ'),并且對任意m∈N(正整數(shù)集合),任意χ1,χ2,…,χm∈X,α1,α2,…,αm∈R,都有K(χi,χj) ≥0,即對任意訓練數(shù)據(jù)χ1,χ2,…,χm∈X,K=(κ(χi,χj) )是正定矩陣。
為了證明函數(shù)
是核函數(shù),根據(jù)定義1,需證明對于任意的訓練樣本χ1,χ2,…,χm和任意的實數(shù)α1,α2,…,αm,都有
其中,K(χi,χj)表示χi和χj之間的核函數(shù)。
對于該函數(shù),有以下推導
因此,對于任意的α1,α2,…,αm,有
然后,定義一個矩陣K,其中,第i行、第j列的元素為Kij= K(χi,χj)。因此,式(12)可以寫成
其中,a=[α1,α2,…,αm]T是一個m維向量。
因此,要證明該函數(shù)是核函數(shù),只需要證明對于任意a,都有aTKa≥0。考慮到K是一個對稱矩陣,因此可以使用它對角化的特征值分解來證明。具體地,設K=UΛUT,其中U是一個正交矩陣,Λ是一個對角矩陣,其對角線上的元素λ1,λ2,…,λm表示K的特征值。由于K是半正定矩陣,因此,所有的特征值都非負。現(xiàn)在,將a表示為Ub的形式,其中,b=UTa。因此,有
由于所有的特征值都非負,上述式子的值都非負。因此,對于任意的訓練樣本χ1,χ2,…,χm和任意的實數(shù)α1,α2,…,αm,都有
2.3 核主成分分析維度約減算法
根據(jù)核主成分分析原理,其維度約減算法的基本步驟如下:

3 實驗結果與分析
實驗代碼使用R 語言(R-4.2.2)編碼實現(xiàn)。實驗環(huán)境為Windows10 64 bit操作系統(tǒng),8 GB內存,Intel(R)Core(TM)i5-8250U CPU@1.60GHz 1.80 GHz。數(shù)據(jù)集詳細描述見表1。使用分類精度作為評價不同數(shù)據(jù)集維度下的機器學習分類方法的分類性能。
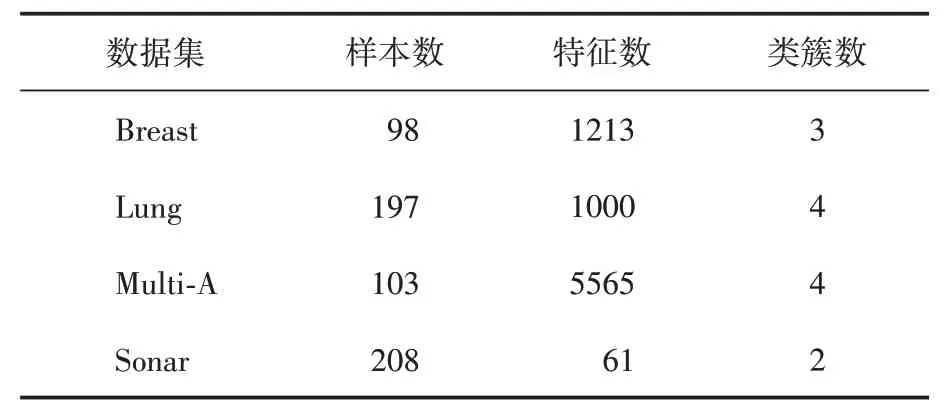
表1 實驗數(shù)據(jù)集描述
3.1 實驗設計
為驗證逆冪核的分類性能,本文利用新的逆冪核和傳統(tǒng)的多項式核、高斯徑向基核及全變量對數(shù)據(jù)集進行維度約減,然后采用支持向量機主流機器學習分類方法對原始數(shù)據(jù)集及已降維的數(shù)據(jù)集進行分類預測。
3.2 對比實驗結果與分析
本文使用的幾種核函數(shù)均帶有參數(shù),徑向高斯(radial basis function,RBF)核函數(shù)參數(shù)γ,其中δ2=50;多項式(polynomial function,POLYF)核函數(shù)參數(shù)r,q,其中r= 0;逆冪(inverse power function,IPF)核函數(shù)參數(shù)c,b。d表示屬性維度。由于核函數(shù)所包含的參數(shù)不多,對每個參數(shù)設置一定的范圍,然后采用簡單的網格搜索法,使得后續(xù)分類算法的精度達到最高。在降維后的數(shù)據(jù)集上進行支持向量機分類預測。同時不對數(shù)據(jù)進行處理,將全變量(full variable,F(xiàn)V)參與支持向量機(SVM)中,上述幾種方法可以記為AV+SVM、POLY+SVM、RBF+SVM、IPF+SVM。其五折交叉驗證精度見表2。

表2 不同核函數(shù)下SVM的五折交叉驗證精度對比
由表2可知,在沒有對數(shù)據(jù)進行維度約減的情況下,直接用SVM 進行分類,其分類精度都比較低,分別為52%、70.52%、19.33%和75.96%。這些情況都表明了支持向量機對高維數(shù)據(jù)集具有一定的敏感性。因此,需要對數(shù)據(jù)進行維度約減,可以看到,在用核主成分進行維度約減后,其分類精度較未進行維度約減前有了顯著提升。尤其對于數(shù)據(jù)特征較多的數(shù)據(jù)集(Multi-A),其分類精度較未進行維度約減前提升較大。但是,不同數(shù)據(jù)集的核表現(xiàn)性能有較大差異,對比高斯徑向基核、多項式核及全變量的情況,運用本文所提出的逆冪核主成分進行的維度約減,其分類精度相對較高,這表明核主成分的維度約減能有效提取原始數(shù)據(jù)的信息。
4 結語
對于高維數(shù)據(jù)集,為了提高后續(xù)機器學習算法的分類性能,證明了一種新的逆冪核主成分,并基于該逆冪核主成分的維度約減方法,對高維數(shù)據(jù)集進行維度約減。通過對四個高維數(shù)據(jù)集的對比實驗,得到與傳統(tǒng)的高斯徑向基核、多項式核及全變量情況的對比研究,結果表明提出的逆冪核主成分的維度約減更加有效地提高了機器學習方法的分類精度。

