考慮層理傾角的硬質砂巖力學行為及破裂響應特征

宋戰平，劉洪珂，鄭 方，程 昀，孫引浩，宋婉雪

(1.西安建筑科技大學 土木工程學院，陜西 西安 710055；2.陜西省巖土與地下空間工程重點實驗室，陜西 西安 710055；3.西安建筑科技大學 隧道與地下結構工程研究所，陜西 西安 710055；4.鹽城工學院土木工程學院，江蘇 鹽城 224051；5.中鐵二十局集團第一工程有限公司，江蘇 蘇州 215000)

硬質砂巖作為典型的沉積巖，受沉積作用和成巖作用的影響，巖體內部存在大量的層理結構面[1]。隨著巖土工程和采礦工程等領域深部開發戰略的實施，復雜地質環境下層理結構面存在顯著的角度差異，是導致巖石力學性能劣化甚至發生破裂的重要原因[2]，并且極易引發洞室圍巖失穩破壞、隧道結構變形開裂等工程病害，直接影響工程建設質量和人民生命安全。因此，探究考慮層理傾角硬質砂巖的力學行為及破裂響應特征對于解決地下空間工程災害問題具有重要的指導意義。

層理結構面的存在使得巖石力學性能顯著降低，而層理傾角是影響含層理結構面巖石力學性能的重要因素。王聰聰等[3]開展不同層理傾角板巖的單軸壓縮試驗，發現層理傾角是單軸抗壓強度、彈性模量和泊松比等力學參數呈現各向異性的重要原因。馮小磊等[4]通過干濕循環作用下頁巖強度試驗對不同層理傾角頁巖的力學特征進行研究，總結抗剪強度指標與層理傾角之間的變化規律。李斌等[5]基于三點彎試驗探究不同層理傾角砂巖斷裂韌度的各向異性，并采用數值模擬方法揭示了層理傾角及層理結構面強度對巖石斷裂力學行為的影響規律。Gao Quan 等[6]采用天然頁巖，通過室內試驗發現軸向垂直層理和軸向平行層理2 種頁巖抗壓強度和抗拉強度的差異性。

在含層理結構面巖石損傷破壞及機理研究方面，國內外眾多專家學者同樣展開了大量研究。趙振峰等[7]構建考慮流固耦合作用下的不同層理傾角頁巖數值模型，準確模擬并預測巖石在滲流?應力耦合作用下的破裂過程和破壞模式，極大程度上為頁巖氣水力壓裂開采提供理論依據。賈炳等[8]利用三軸壓縮試驗對煤巖加載過程中的聲發射差異性進行分析，認為層理結構面可以顯著影響巖石的變形破壞特征，集中體現在軸向垂直層理煤巖以整體變形破壞為主，而軸向平行層理煤巖以局部變形破壞為主。H.Niandou 等[9]基于三軸壓縮試驗和循環加卸載試驗對含層理結構面Tournemire 頁巖的彈性響應和塑性變形進行各向異性研究，發現含層理結構面巖石的破壞模式與加載方向和圍壓大小有關。

綜上所述，目前關于含層理結構面巖石的力學性能及損傷破壞研究已經取得一定有益成果，但是考慮層理傾角的硬質砂巖力學行為及破裂響應特征尚不明確，有待進一步研究。因此，筆者基于不同層理傾角硬質砂巖的單軸壓縮試驗，一方面探究層理傾角影響下硬質砂巖的應力?應變關系和力學特征的各向異性，另一方面揭示硬質砂巖的宏觀破壞模式及損傷破壞過程中的碎塊分形特征，以期為開展不同層理傾角巖石的力學行為及破裂響應特征研究提供理論依據與指導。

1 試驗材料與試驗方案

1.1 試驗砂巖

試驗巖樣選取四川成都地區的層狀硬質砂巖，平均密度約為2.47 g/cm3，單軸飽和抗壓強度大于30 MPa，外觀呈青灰色且無明顯的顏色變化，層理天然勻稱、發育顯著，層理結構面間距為1～2 mm，無明顯缺陷。通過X 射線衍射(XRD)測定硬質砂巖的礦物組成，具體為：斜長石(質量分數71%，下同)、石英(10%)、方解石(4%)、蛭石(4%)、鉀長石(3%)、赤鐵礦(2%)、閃石(2%)、蛇紋石(2%)、綠泥石(1%) 及其他成分(1%)。同時，利用掃描電子顯微鏡(SEM)對硬質砂巖的層理結構面進行觀察，分別從放大倍數為500 倍和2 000 倍觀察其微觀結構(圖1)。晶體顆粒表面光滑無裂隙、結構較為完整、排列相對緊密，顆粒之間通過膠結物黏結形成骨架，而膠結物呈絮狀分布，微裂隙發育顯著，這是在微觀層面上引起硬質砂巖力學性能劣化的原因。

1.2 巖樣制備

考慮到沉積巖獨特的成巖特性賦予其典型的層理特征，為深入探究硬質砂巖力學特征的各向異性，本次試驗分別制備了5 種不同層理傾角下(0°、22.5°、45.0°、67.5°、90.0°)直徑50 mm、高100 mm 的標準圓柱狀硬質砂巖試樣(圖2)，其中層理傾角是指層理結構面與水平面之間的夾角。

巖樣具體制備過程如下：步驟Ⅰ，準備新鮮完整巖塊；

步驟Ⅱ，通過切石機將巖塊切割成具有水平層理的長方體狀巖塊；步驟Ⅲ，利用鉆石機按照不同的鉆取方向進行取心；步驟Ⅳ，取心成功后先用切石機將2 個端面切割平整，再經磨石機打磨拋光，從而得到試驗所需巖樣。端面的不平行度和不垂直度嚴格符合GB/T 50266?2013《工程巖體試驗方法標準》[10]的要求，分別控制在≤0.05 mm 和≤0.25°。

1.3 試驗設備

本試驗在西安建筑科技大學巖土與地下空間工程重點實驗室完成，采用WAW-600B 型微機控制電液伺服巖石拉壓試驗機，該設備主要由試驗機主機(壓縮夾具、高精度負荷傳感器和伺服控制專用油源)和PC機控制系統組成，如圖3 所示。該試驗機具有應力控制和應變控制2 種加載方式，可提供的最大試驗力為600 kN，試驗力分辨率為0.10 kN，試驗力誤差在±1%以內。

1.4 試驗方案

本試驗主要研究層理傾角對硬質砂巖力學行為和破裂響應特征的影響，基于此試驗目的，對5 種不同層理傾角的硬質砂巖試樣進行單軸壓縮試驗。

試驗分為以下3 步進行：

(1)將制備好的巖樣依次進行質量及密度測試，剔除破損、質量和密度異常的巖樣。將測試結果合格的巖樣根據層理傾角分為5 組，每組設置2 個平行試驗，一共10 個試樣，分別進行編號(表1)。

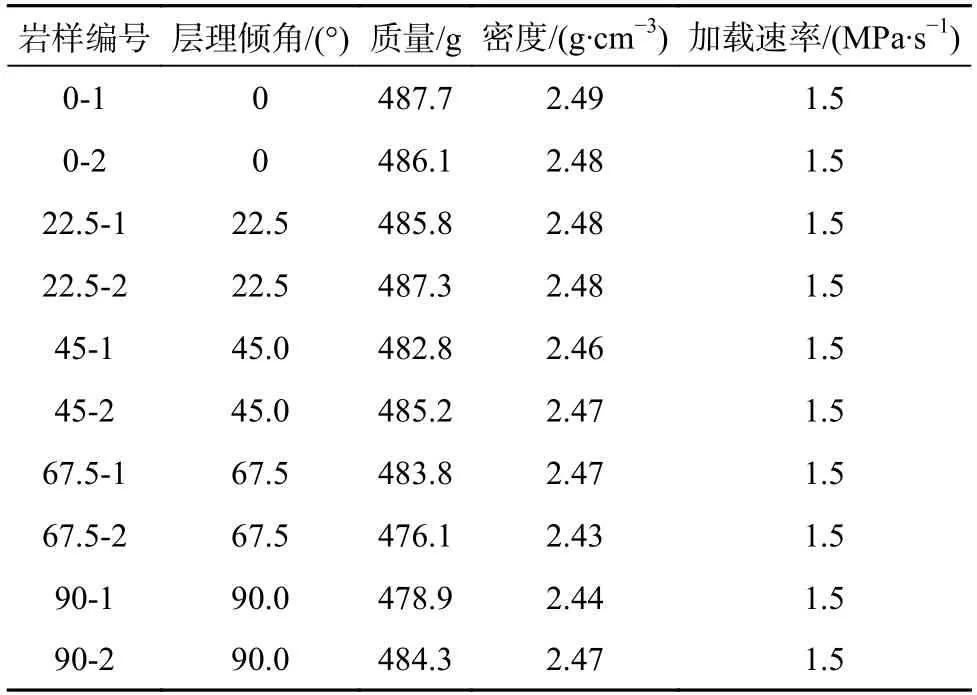
表1 硬質砂巖單軸壓縮試驗方案Table 1 Uniaxial compression test scheme for hard sandstone samples

(2)為消除端面摩阻力的影響，在巖樣兩端涂抹潤滑劑。正式試驗之前進行軸向荷載為0.20 kN 的初始預壓，確保巖樣同試驗機壓縮夾具有效接觸。受預壓荷載的影響，應變初始值約為0[11]。

(3)單軸壓縮試驗全程采用應力控制的方式進行加載，以1.5 MPa/s 的加載速率至巖樣破壞，應力?應變曲線由PC 機控制系統自動采集。本試驗將選取2個平行試驗中最具代表性的試驗結果作為最終試驗結果。

2 力學行為分析

2.1 應力?應變曲線

單軸壓縮下不同層理傾角硬質砂巖的應力?應變曲線。

如圖4 所示。從圖中可以看出，應力?應變曲線在整體形態分布方面具有相似性，但由于層理傾角的不同，局部表現出一定的差異性。硬質砂巖的應力?應變曲線可近似分成4 個區段，分別為壓密階段、彈性階段、塑性階段和脆性階段。

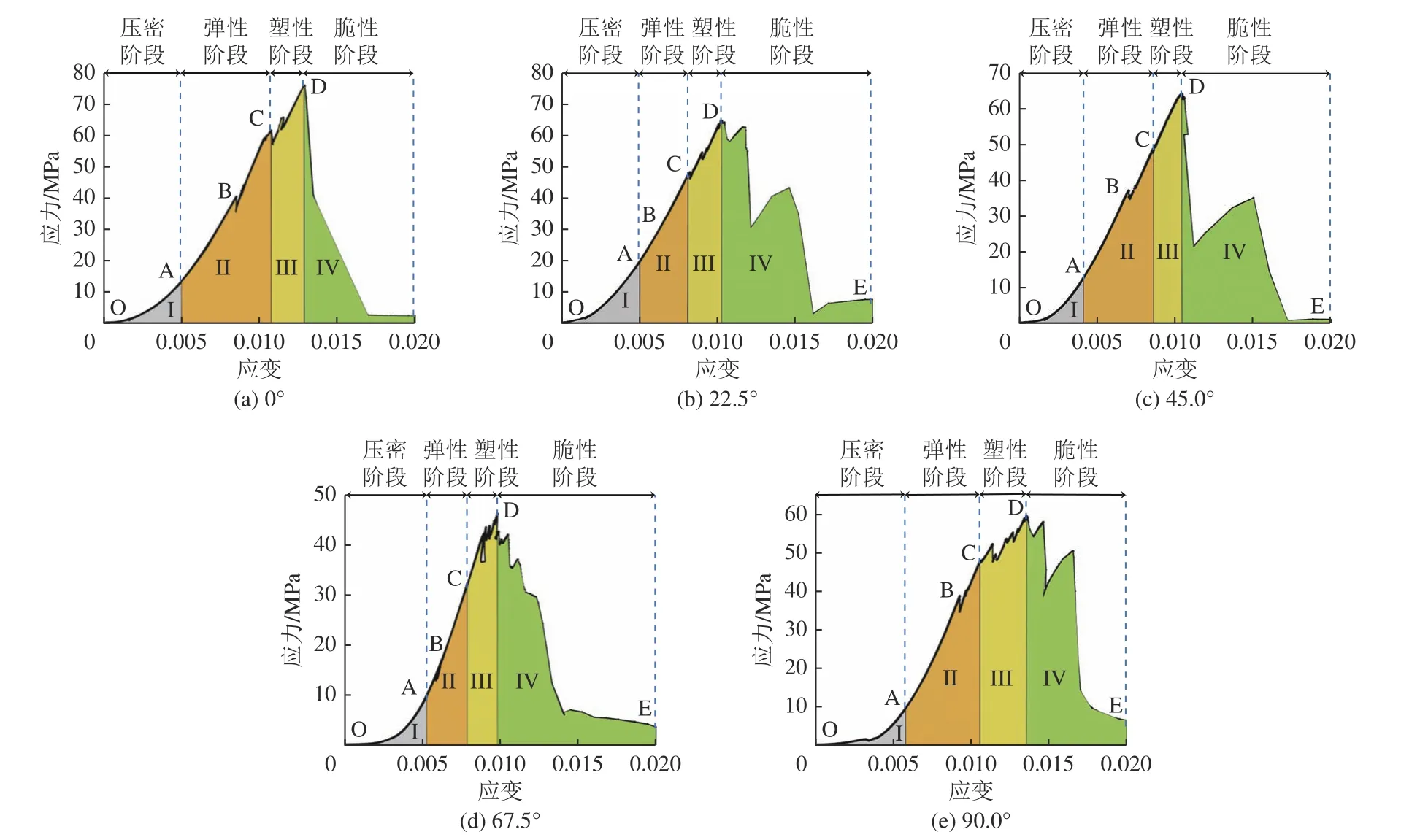
圖4 不同層理傾角硬質砂巖的應力?應變曲線Fig.4 Stress-strain curves of hard sandstones with different bedding dip angles

1)壓密階段Ⅰ(OA 段)

該階段持續時間占全過程的10%～14%，其應力?應變曲線近似呈向上彎曲增長趨勢，應力最大值分布在10 MPa 左右，應變最大值分布在0.005 左右。應力?應變曲線的斜率隨著應力的增加表現出先緩慢增長后急速增長的特征，該特征隨著層理傾角的增大越發突出，在傾角為67.5°和90.0°時表現得尤為明顯。分析原因認為，壓密階段是由于細微裂隙受壓閉合造成的，加載初期變形較大，曲線較為平緩、增速緩慢。傾角較大時，原生裂隙閉合和層理面微滑移抵消導致巖石的剛度增加，曲線陡峭增長。

2)彈性階段Ⅱ(AC 段)

彈性階段(AC 段)可分為彈性變形階段(AB 段)和裂紋穩定擴展階段(BC 段)[12]，該階段持續時間占全過程的25%～40%，其應力?應變關系近似于一條直線。傾角為0°時出現應力最大值64 MPa，傾角67.5°時出現應力最小值32 MPa，前者約為后者的2 倍，說明層理傾角的變化對處于彈性階段巖石的強度存在顯著的影響。巖石進入彈性變形階段，內部裂隙閉合完全，表面基本完整，無明顯裂紋。隨著荷載的繼續增加，巖石進入裂紋穩定擴展階段，原生裂隙開始擴展，表面產生細微裂紋并伴隨有破裂聲，新裂紋的起裂方向與最大壓應力的作用方向保持一致[13]，此時的應力?應變曲線出現小幅度下跌。

3)塑性階段Ⅲ(CD 段)

該階段處于裂紋非穩定擴展階段，持續時間占全過程的10%～25%。隨著荷載的進一步增加，巖樣表面出現明顯擴張裂紋并伴隨有顯著破裂聲，傾角為45.0°、67.5°的巖樣發生碎片飛濺，體積由壓縮轉為擴容，應力達到峰值強度。同時，該階段的應力?應變曲線隨層理傾角的變化表現出一定差異，可概括為兩類變化[14]。傾角較小時(0°、22.5°、45.0°)，峰值附近曲線無明顯的上下波動，近似為單峰曲線；傾角較大時(67.5°、90.0°)，峰值附近曲線呈鋸齒狀變化，近似為多峰曲線。分析原因認為，傾角較小時，巖樣破壞受層理面影響較小，表現為脆性破壞；傾角較大時，層理面對巖樣的破壞起主導作用，因此在荷載作用下易發生層理面滑移，造成應力跌落，從而導致曲線的波動。

4)脆性階段Ⅳ(DE 段)

該階段處于脆性破壞階段，由于本試驗所使用的壓力機并非變形小的剛性壓力機[15]，故巖樣在峰值處突然破壞，發生急驟變形并伴隨有顯著爆鳴聲，碎片猛烈飛濺。應力?應變曲線驟然下降，且產生回彈現象，傾角為22.5°、45.0°、90.0°巖樣的回彈現象特別明顯，這說明巖樣在破壞后并沒有完全失穩，仍具有一定的剛度和承載能力。

通過對單軸壓縮下不同層理傾角硬質砂巖的應力?應變曲線進行對比分析，認為層理結構面的存在增加了硬質砂巖的非均質性，降低了其整體強度，并且層理傾角極易改變硬質砂巖內部的應力狀態，從而導致加載過程中應力?應變曲線呈現出差異性，主要體現在以下2 個方面。層理傾角的增加，導致硬質砂巖強度的劣化程度提高，尤其傾角為67.5°時，劣化程度最高。分析原因認為，層理結構面晶體顆粒之間的膠結能力較差，降低了硬質砂巖抵抗變形破壞的能力。傾角為0°時，即軸向荷載與層理結構面相互垂直，對硬質砂巖的強度影響較小；傾角為67.5°時，基本達到了理論剪切破壞面角度(45.0°+φ/2)，φ為巖石的內摩擦角，此時發生層理結構面滑移，對硬質砂巖的強度影響較大。傾角為0°和90.0°硬質砂巖的應力?應變曲線峰值滯后性更加明顯。分析原因認為，傾角為0°和90.0°時，軸向荷載與層理結構面相互垂直、平行，此時硬質砂巖可近似視為橫觀各向同性體。加載過程中，大量彈性能在硬質砂巖內部聚集，能量積聚率較大，表現為在應變為0.013 附近處發生失穩破壞。而其余傾角的硬質砂巖由于層理結構面造成損傷，能量積聚率較小，表現為在應變為0.01 附近處發生失穩破壞。

2.2 峰值應力、應變

為了量化研究層理傾角對硬質砂巖力學性能的影響，根據圖4 中應力?應變曲線得到不同層理傾角硬質砂巖的峰值應力σd和峰值應變εd，分析兩者同層理傾角的數值關系對于預測巖石破壞具有重要的參考意義。圖5 為硬質砂巖的峰值應力和峰值應變與層理傾角的變化關系曲線。如圖所示，峰值應力和峰值應變隨著層理傾角的增大均近似表現為先減小后增大的類“W”形變化趨勢。

從小學數學當前實際的教學情況來看，教學效果并不是十分理想，之所以會出現這種情況，主要是因為一些教師仍然在使用比較傳統的教學方法，而這種方式最大的弊端就是無法激發學生的學習熱情，所以為了改變這種情況，教師首先應該做的就是激發學生學習熱情。因此，在啟發式教學中，教師可以從學生的生活出發，利用學生比較熟悉的生活事物或生活場景來創設教學情境，這樣一來，可以使教學內容的趣味性增加，從而更好地調動學生的學習熱情，只有這樣，才能為啟發式教學的順利展開奠定比較好的基礎。

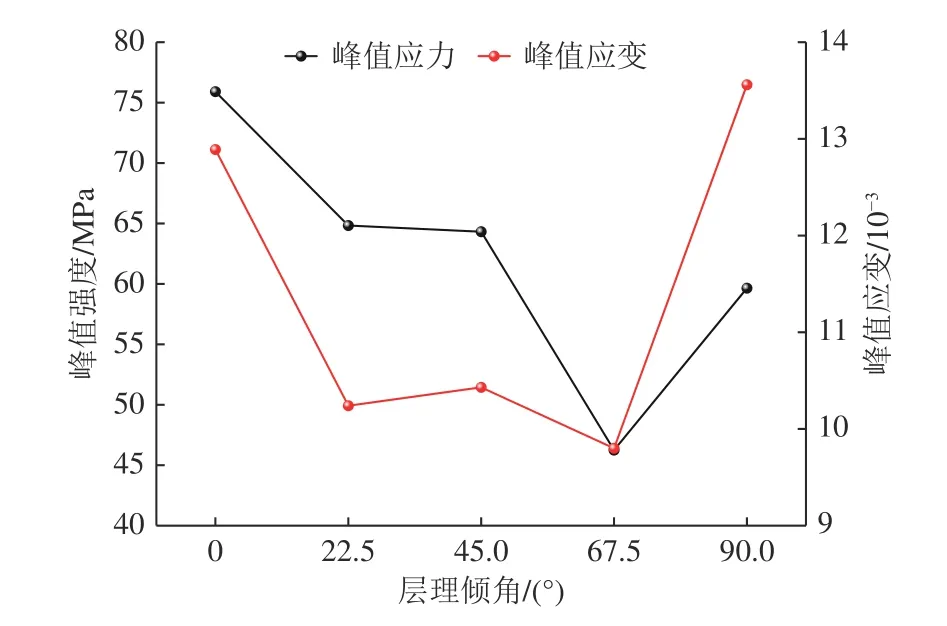
圖5 力學參數與層理傾角的變化關系曲線Fig.5 Curves showing relationships between mechanical parameters and the bedding dip angle

傾角為0°、22.5°、45.0°、67.5°、90.0°所對應的峰值應力σd依次為75.91、64.83、64.32、46.25、59.65 MPa，峰值應力σd在傾角為0°和67.5°時分別達到最大值75.91 MPa 和最小值46.25 MPa，同傾角0°相比，22.5°、45.0°、67.5°、90.0°所對應的峰值應力σd分別下降了15%、15%、39%、21%。分析原因認為，傾角為0°時，軸向荷載與層理結構面相互垂直，巖石破壞主要取決于顆粒間的摩擦強度和黏聚強度；傾角大于0°時，出現層理結構面滑移現象，且巖石存在最不利層理結構面。在達到最不利層理結構面前后，巖石破壞趨向于沿層理結構面發生滑移，在達到最不利層理結構面時，巖石在最不利層理結構面發生滑移剪切破壞，峰值應力下降甚至達到最小值。

傾角為0°、22.5°、45.0°、67.5°、90.0°所對應的峰值應變εd依次為12.89×10?3、10.24×10?3、10.43×10?3、9.80×10?3、13.56×10?3，峰值應變εd在傾角為90.0°、0°和67.5°時分別達到最大值13.56×10?3、次大值12.89×10?3和最小值9.80×10?3，同傾角0°相比，22.5°、45.0°、67.5°所對應的峰值應變εd分別下降了21%、19%、24%。分析原因認為，傾角為90.0°的巖石產生壓桿效應，趨向于劈裂破壞；傾角為67.5°的巖石發生最不利層理結構面滑移剪切破壞，峰值應變同峰值應力達到最小值。此外，層理傾角對硬質砂巖應變的影響變化均勻，削弱程度在20%左右，即層理傾角對硬質砂巖應力的影響同比應變更為顯著。

2.3 各向異性特征

通過2.2 節分析發現，層理傾角改變影響峰值應力和峰值應變的大小，說明硬質砂巖具有各向異性特征，彈性模量E常用來描述巖石的變形特性，各向異性可能同樣對其具有影響。為了量化各向異性對巖石力學參數的影響，引入各向異性度[16]的概念，其表達式為：

式中：k為各向異性度；Pmax為峰值應力最大值、峰值應變最大值、彈性模量最大值等參數；Pmin為峰值應力最小值、峰值應變最小值、彈性模量最小值等參數。

非線性彈性模量E的精確取值較為困難，本文將應力?應變曲線上原點與某點(峰值應力的50%)連接直線的斜率作為彈性模量。根據相關曲線和公式計算得到不同層理傾角硬質砂巖的峰值應力σd、峰值應變εd和彈性模量E的各向異性度。以峰值應力、峰值應變和彈性模量計算得到的各向異性度分別為1.64、1.38 和1.32，受層理傾角的影響，硬質砂巖表現出一定的各向異性特征，但各向異性特征并不明顯，經判斷硬質砂巖屬于低各向異性巖石。由于以彈性模量計算得到的各向異性度幾乎不受試驗類型的影響，使用彈性模量作為巖石各向異性度的衡量標準[17]，峰值應變的各向異性度略高于彈性模量，而峰值應力的各向異性度同比彈性模量增長24%，說明峰值應力的各向異性特征較峰值應變和彈性模量明顯，層理傾角對峰值應力的擾動偏大，這與文獻[18]未施加圍壓狀態下的研究情況基本一致。

3 破裂響應特征分析

3.1 宏觀破壞模式

單軸壓縮下由于巖石無側向壓力的約束，其破壞模式較為復雜。根據大量的試驗和觀察證明，巖石在單軸壓縮條件下的破壞模式大致分為X 型共軛剪切破壞、單斜面剪切破壞和張拉破壞3 種類型[19]。影響破壞模式的因素包括礦物成分、層理特征、加壓方式等，本文只探究單軸壓縮條件和層理傾角變化對巖石破壞模式的影響。

參照上文標準，同樣選取2 個平行試驗中最具代表性的試驗結果作為最終試驗結果。圖6 是不同層理傾角的硬質砂巖在單軸壓縮條件下的宏觀破壞模式圖。如圖所示，硬質砂巖的破壞模式受各向異性的影響，但同層理傾角之間表現出一定的規律性。傾角為0°時，巖樣出現典型的X 型共軛剪切裂紋和單斜面剪切裂紋，2 種裂紋發生貫通，局部出現橫向張拉裂紋，硬質砂巖主要發生剪切破壞；傾角為22.5°時，巖樣出現未貫通的X 型共軛剪切裂紋和貫通的單斜面剪切裂紋，且形成一條主剪切面，局部出現少量劈裂裂紋，硬質砂巖以剪切破壞為主；傾角為45.0°時，巖樣表面巖體與巖心發生脫離，表面巖體中部斷折，巖心形成一條貫通的主斷裂面，硬質砂巖破壞模式復雜，表現為剪切張拉復合破壞；傾角為67.5°時，巖樣出現2 條沿著層理結構面方向的主剪切面且發生滑移，這與理論剪切破壞面角度(45.0°+φ/2)基本一致，底部出現細密網狀裂紋，此時硬質砂巖發生層理結構面剪切破壞；傾角為90.0°時，巖樣出現多條貫通的豎向裂紋，局部伴隨少量斷折裂紋，硬質砂巖發生劈裂破壞。

圖6 硬質砂巖樣宏觀破壞模式Fig.6 Macroscopic failure modes of hard sandstone samples

3.2 碎塊質量特征

單軸壓縮下硬質砂巖試樣破壞，產生不同尺寸和質量的碎塊，其呈現出一定的分布規律，即碎塊分布特征。為進一步研究碎塊質量分布特征，采用篩分法[20]對硬質砂巖碎塊進行分類統計，根據所用的不同孔徑石篩將碎塊分為9 個分布區間(表2)。按照相關分類標準，將分布區間r≤5 mm、5 mm＜r≤20 mm、20 mm＜r≤50 mm、r＞50 mm 的碎塊分別劃分到細粒、細塊、中塊和粗塊類別，其中，分布區間為20 mm＜r≤40 mm的碎塊為主碎塊。不同層理傾角硬質砂巖碎塊的分布區間及質量百分比見表2，“?”表示該分布區間未出現相應尺寸的碎塊，并根據表2 中的數據繪制硬質砂巖碎塊的質量分布直方圖，如圖7 所示。

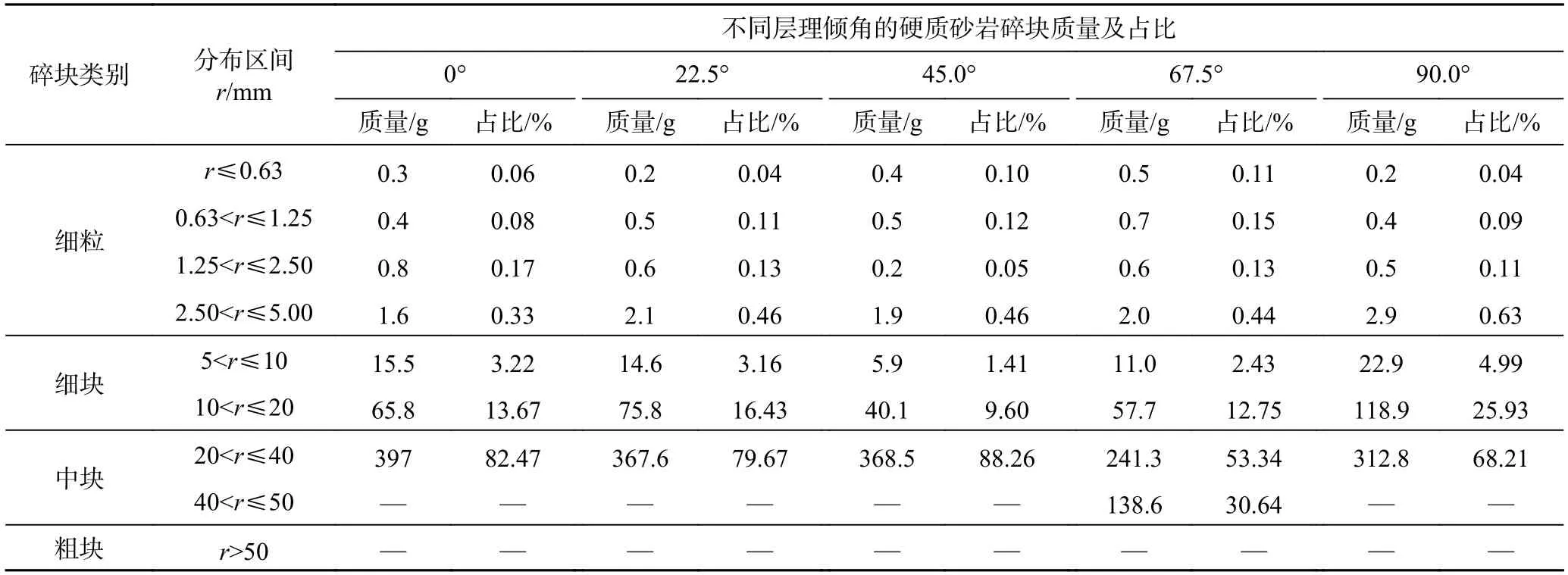
表2 硬質砂巖碎塊的分布區間及質量百分比Table 2 Size distributions and mass percentages of hard sandstone fragments

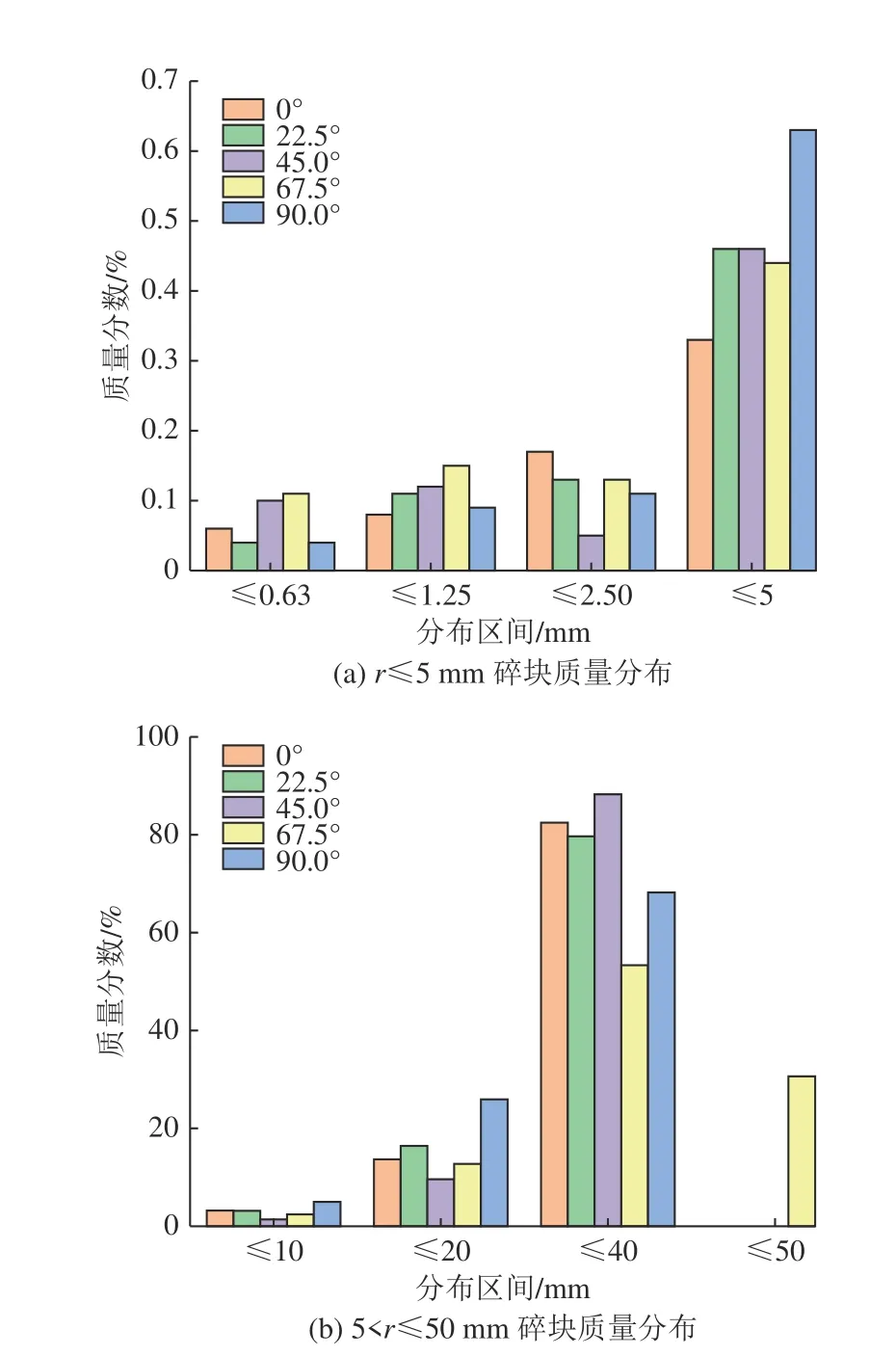
圖7 硬質砂巖碎塊質量分布直方圖Fig.7 Histograms showing the mass percentages of hard sandstone fragments

由表2 和圖7 可知，不同層理傾角的硬質砂巖試樣在單軸壓縮條件下破壞形成的碎塊以中塊、細塊和細粒為主，未出現尺寸＞50 mm 的粗塊。傾角為67.5°的硬質砂巖出現尺寸＞40 mm 且≤50 mm 的碎塊，其余傾角的硬質砂巖碎塊尺寸均≤40 mm。其中，分布區間20 mm＜r≤40 mm 的主碎塊質量占碎塊總質量的53.34%～88.26%，即中塊作為巖石碎裂后的主要碎塊類別。當傾角從0°增加至90.0°時，分布區間r≤5 mm的碎塊質量小于3 g，質量分數小于1%，相同分布區間的中塊和細塊碎塊的質量分數差異性明顯大于細粒碎塊，說明層理傾角對細粒碎塊的質量分布影響較小，這也與巖石的宏觀破壞模式有關。

3.3 碎塊分形特征

分形理論[21-22]研究巖石碎塊的分布規律，在巖石破碎領域得到廣泛應用。本文以不同層理傾角的硬質砂巖碎塊為研究對象，采用碎塊的質量?粒徑分形計算方法[23]進行分形特征研究，其分布計算方程[24]如下：

式中：r為巖石碎塊的特征粒徑，即各分布區間的篩分尺寸；M(r)為等效粒徑R小于特征粒徑r的巖石碎塊質量；MT為巖石碎塊的總質量；Dr為巖石碎塊的分形維數。

巖石由整體破壞為碎塊的過程中，其等效粒徑R存在以下等式關系：

式中：V為巖石碎塊的等效體積；l、d、h分別為巖石碎塊的等效長度、寬度、高度。

對式(2)兩邊取自然對數可得：

由式(4)可知，雙對數 ln[M(r)/MT] 與 lnr存在線性關系，3?Dr為雙對數坐標下的線性斜率值，線性關系越明顯，則巖石碎塊的分形特征越好。因此，利用單軸壓縮試驗并通過篩分法可以統計不同分布區間巖石碎塊的質量、粒徑等物理參數，繪制質量與粒徑關系曲線，通過數值回歸可確定巖石碎塊的分形維數。這里根據上文統計結果進行數值擬合，繪制回歸關系，如圖8 所示。

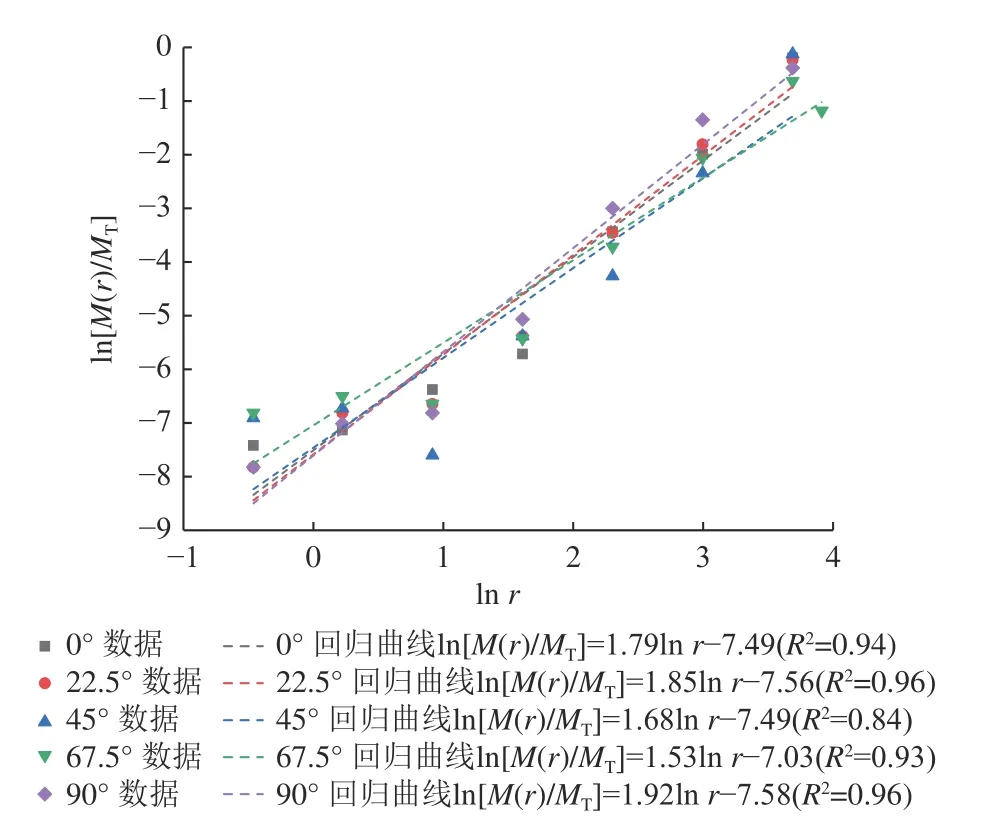
圖8 硬質砂巖碎塊質量與粒徑回歸曲線Fig.8 Regression curves of the mass and particle size of hard sandstone fragments

由圖8 可知，本文所研究的硬質砂巖碎塊質量與粒徑回歸曲線的相關系數R2高達0.84～0.96，線性相關性明顯，即分形特征良好，表明不同層理傾角的硬質砂巖破碎具有良好的自相似性。傾角為0°、22.5°、45.0°、67.5°、90.0°的硬質砂巖碎塊的回歸曲線斜率分別為1.79、1.85、1.68、1.53、1.92，曲線斜率呈現出先減小后增大的趨勢，最小斜率出現在傾角67.5°的數據，和上文研究結果相互印證。分形維數可以定量表征巖石的破碎程度，分形維數值越大，巖石的破碎程度越高。傾角為0°、22.5°、45.0°、67.5°、90.0°的硬質砂巖碎塊的分形維數分別為1.21、1.15、1.32、1.47、1.08，分形維數值均位于1～2，且在傾角為67.5°時達到最大值，說明大尺寸分布區間的碎塊所占比例較大。層理傾角與巖石破裂具有交互的應力響應，應力協調和損傷積累較為充分，從而導致巖石更容易發生失穩和破裂。

4 結論

a.層理傾角較小的硬質砂巖應力?應變曲線表現出單峰的變化規律，而層理傾角較大的硬質砂巖應力?應變曲線表現出多峰的變化規律；層理傾角對硬質砂巖應力的影響明顯大于應變，峰值應力σd和峰值應變εd均在最不利層理結構面達到最小值，且硬質砂巖表現出低各向異性特征。

b.層理傾角對硬質砂巖的破壞模式具有顯著影響，隨著層理傾角的增大，硬質砂巖呈現出剪切破壞?剪切張拉復合破壞?層理結構面剪切破壞?劈裂破壞的損傷破壞演化規律。

c.研究層理傾角對含層理結構面巖石的力學行為及破裂響應特征的影響，對實現地下空間工程災害防治具有一定的理論價值。層理傾向同樣影響含層理結構面巖石的力學性能，建議下一步綜合考慮層理傾角和層理傾向的變化以及滲透水壓力作用下的含層理結構面巖石在三軸壓縮條件下的變形規律研究工作。