無頻間鐘偏差改正的BDS-2三頻非組合PPP隨機模型優化
周長江,余海鋒,王林偉,雷云平,岳彩亞
(1. 中水北方勘測設計研究有限責任公司,天津 300222; 2. 山西省國土空間調查規劃中心, 山西 太原 030000; 3. 聊城大學地理與環境學院,山東 聊城 252000)
隨著計算機、通信和芯片等軟硬件設備的不斷升級和發展,多個全球導航衛星系統(GNSS)已具備播發多頻觀測數據的能力,為消除或減弱電離層延遲影響、抑制觀測噪聲放大提供了新方法,同時也為增強衛星定位幾何強度和解算容錯率提供了基礎支撐[1-3]。然而,由于當前國際GNSS服務組織(IGS)分析中心發布的鐘差產品中包含了無電離層組合的衛星端相位硬件延遲時變部分,導致當鐘差產品被用到第3個頻率時,使得全球定位系統(GPS)和北斗二號衛星系統(BDS-2)精密單點定位(PPP)驗后殘差出現較大波動,需要額外的處理頻點之間的偏差,稱為頻間鐘偏差(inter-frequency clock deviation,IFCB)[4]。相關研究已證明GPS Block IIF和BDS-2衛星IFCB變化量級最大可分別達30 cm和5 cm,這對于驗后殘差僅在厘米級的PPP技術而言必須加以改正[5]。為此,文獻[6-8]提出了兩個無電離層組合做差的歷元間差分方法、星間歷元間差分方法以及常數部分和時變部分分開解算的方法估計IFCB。利用上述估計的IFCB可直接用于PPP事后解算模型改正中,或是通過對IFCB建立預報模型進行實時多頻PPP或PPP網解,相關結論已證明基于上述IFCB建模改正方法可較好地滿足GPS Block IIF衛星多頻精密定位。
而對于BDS-2衛星的IFCB,由于其影響量級相對較小,當利用上述方法進行IFCB建模改正時精度提升有限,并且會增強多頻PPP計算負擔[9]。為此,眾多學者在處理BDS-2三頻非組合PPP時,主要傾向于不加IFCB改正,且將3個頻率載波觀測值權重設置成相等或根據經驗降低第三頻率觀測值權重。因此,為了客觀評估無IFCB改正時BDS-2三頻非組合PPP最優隨機模型和提升多頻觀測數據融合定位性能,本文提出一種枚舉方法重點分析當無IFCB改正時,BDS-2第三頻率觀測值權重的最優取值,并進行三頻非組合PPP靜態和動態定位性能驗證。
1 BDS-2三頻非組合PPP隨機模型優化
1.1 三頻非組合PPP定位模型
原始多頻(j=1,2,3,…)非差偽距和載波相位觀測方程可表示[10-11]為
(1)
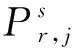

(2)
基于式(2),文獻[13]將接收機鐘差表達成了同種方式并進行了多頻非組合PPP推導。為了突出重點,本文直接給出了顧及IFCB的BDS-2三頻非組合PPP偽距和相位觀測方程實用公式,為
(3)
(4)
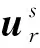
(5)
(6)
1.2 隨機模型優化
文獻[9]已證明在附有IFCB約束的條件下BDS-2三頻非組合PPP定位性能得到小幅度提升,但需提前估計IFCB,增加了程序計算負擔和時間。因此,本文重點在未顧及IFCB對第三頻率觀測值改正的情況下,提出一種載波相位觀測值權重枚舉方法,分析并評估第三頻率載波相位觀測值與前兩個頻率觀測值最優權比配置方法,以實現BDS-2三頻非組合PPP隨機模型優化。即
(7)
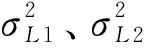

表1 不同方案下c的取值
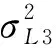
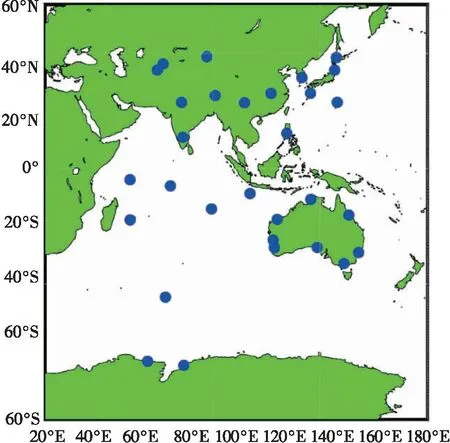
圖1 MGEX跟蹤站分布

圖2 不同方案下2小時PPP解坐標殘差
2 試驗結果與分析
為了進一步驗證BDS-2三頻非組合PPP優化隨機模型的可用性,本文基于3種方案分別實施了亞太地區6個測站三頻非組合PPP靜態和動態解算。其中,方案1為無IFCB改正的BDS-2三頻非組合PPP;方案2為基于真實IFCB改正值的三頻非組合PPP;方案3為將c取值為3.0,既將第三頻率載波相位觀測值的權重降低3倍。表2中給出了6個測站的詳細信息,均可正常接收BDS-2觀測值,數據采樣率為30 s,其他解算參數配置與隨機模型優化部分完全一致。值得說明的是用于性能驗證的6個測站并未參與隨機模型優化評估。
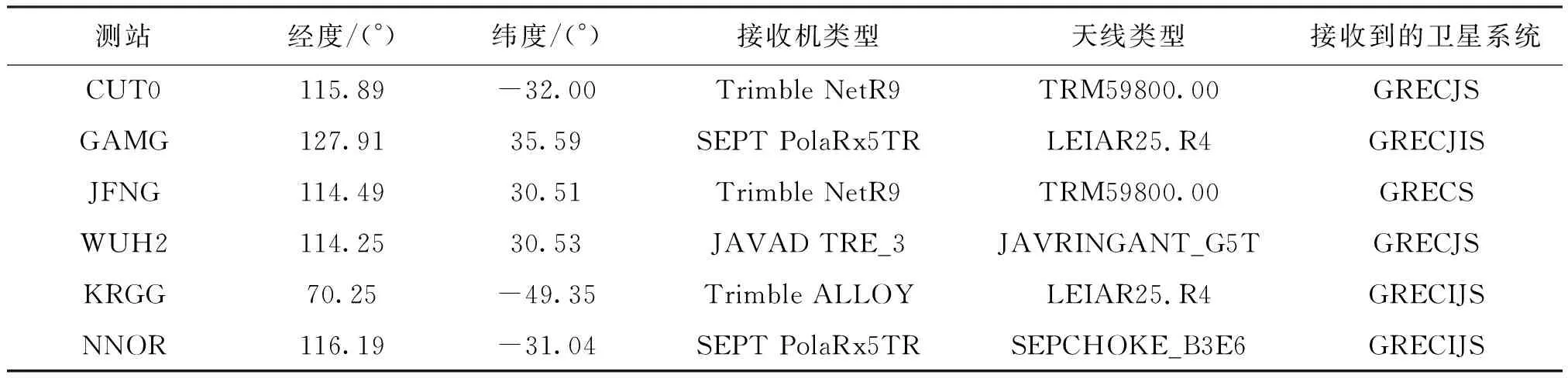
表2 各MEGX測站詳細信息
2.1 BDS-2三頻非組合PPP靜態定位性能驗證
圖3中以CUT0站和NNOR站為例,展示了不同方案下的BDS-2三頻非組合PPP坐標殘差序列。整體分析可知,方案2和方案3的時間序列殘差基本重合,說明將BDS-2第三頻率權重降低為原來的3倍具有與采用真實IFCB改正同等的定位效果,且方案2和方案3坐標殘差序列均優于方案1,特別是在初始收斂階段。
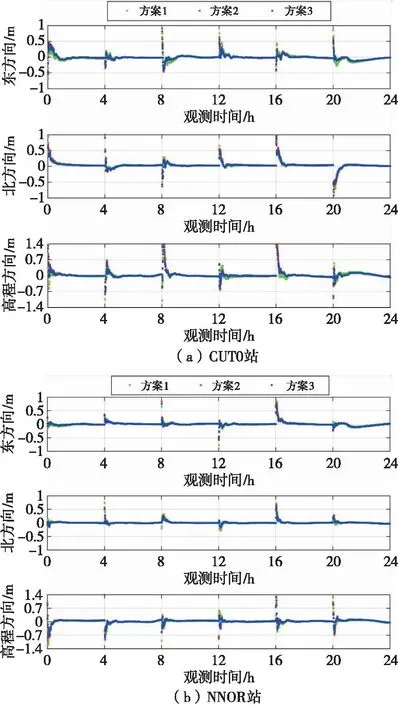
圖3 CUT0站和NNOR站不同方案BDS-2 三頻非組合PPP殘差序列
為了詳細分析不同方案下坐標解算精度差異,將每個測站分為6個弧段,并詳細統計了所有測站36個弧段坐標定位精度,統計時以IGS發布的SNX文件中的各測站坐標作為真值[15],將每個弧段最后半小時坐標殘差取平均作為解算精度,進而消除異常歷元對統計精度的影響。表3中給出了3種方案下所有弧段PPP解算坐標平均殘差,分析可知,當顧及IFCB影響條件下BDS-2三頻非組合PPP定位精度可得到進一步提升,對于方案1和方案3,當BDS-2第三頻率權重降低為原來的3倍時,坐標解算精度在東、北和高程方向分別可提升10.1%、5.7%和7.1%。對于方案2和方案3,定位精度基本一致。

表3 不同方案BDS-2三頻非組合PPP平均殘差和收斂時間
為了分析優化的BDS-2三頻非組合PPP隨機模型對收斂時間的改善,表3中同樣統計所有弧段收斂到10 cm所用的時間。其中,收斂時間定義為坐標東、北和高程方向坐標殘差均收斂到10 cm以內所用的時間,且在后續歷元保持穩定。為了能得到客觀的收斂時間,本文在對36個弧段收斂時間平均時,以3倍的中誤差作為閾值進行異常值的剔除。對表3分析可知,當顧及IFCB的影響時,可進一步提升坐標殘差收斂速度。其中,相對于方案1,采用方案2和方案3進行PPP解算時,在東、北和高程方向可分別提升約11.0、4.8和9.2 min,并且同樣展示出了方案2和方案3具有同等效果的收斂速度提升。
2.2 BDS-2三頻非組合PPP動態性能驗證
為了驗證優化的BDS-2三頻非組合PPP隨機模型的動態定位性能,分別基于3種方案實施了6個測站動態解算,坐標的過程噪聲均方誤差設置為60 m。限于篇幅,圖4中僅以JFNG站為例展示了該點定位殘差,表4中統計了6個測站平均均方根誤差(RMS)。整體分析可知,3種方案下均可實現厘米級定位精度,方案2和方案3定位殘差序列具有較高的重合度,說明此兩種方案動態定位結果較為接近,且均優于方案1。基于表4進一步分析可知,相對于方案1,在顧及IFCB影響的情況下,方案2和方案3均可實現坐標精度小幅度改善,而方案2和方案3定位精度則表現得基本一致。通過統計平均RMS值可知,相對于方案1,當采用降低第三頻率相位觀測值權重的方法時,可分別實現東、北和高程方向10.7%、6.1%和9.2%的精度提升。

圖4 JFNG站不同方案BDS-2三頻動態非組合PPP時間序列
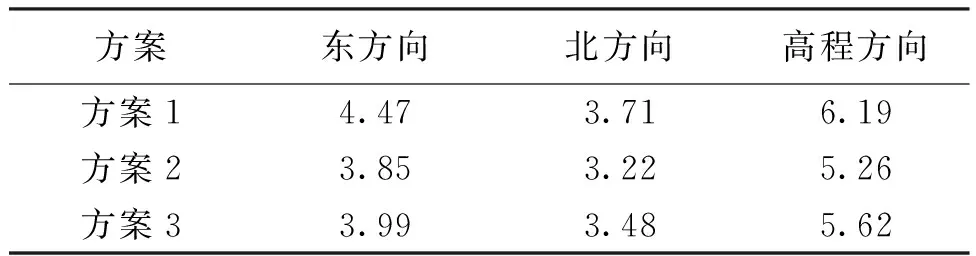
表4 不同方案BDS-2三頻非組合PPP動態殘差平均RMS cm
3 結 語
本文針對BDS-2傳統鐘差產品無法直接應用于多頻精密單點定位的問題,提出了一種BDS-2三頻非組合PPP隨機模型優化方法,并通過亞太地區大量MGEX跟蹤站實測數據進行驗證。結果表明,當無IFCB改正時,可將第三頻率相位觀測值方差放大到原始方差的2~4倍。為了進一步驗證優化的隨機模型,基于亞太地區6個MGEX站分別實施了無IFCB改正,利用真實IFCB改正和將第三頻率相位觀測值方差放大到原始值3倍的BDS-2三頻非組合PPP動態和靜態解。結果表明,無論是動態解還是靜態解,當顧及IFCB影響的情況下均可實現定位精度和收斂速度改善,相對于采用真實IFCB改正,采用將BDS-2第三頻率觀測值權重降低為原來3倍的方法基本具有同等PPP性能改善,但可避免對IFCB進行事前估計的問題。

