觀測不確定性下的高效貝葉斯更新方法及其在機翼結構中的應用

于汀，李璐祎，劉昱杉，常澤明

西北工業大學 航空學院，西安 710072

20 世紀60 年代初，貝葉斯模型更新開始受到結構工程師的廣泛關注，最早被用于土木工程結構分析和鑒定，后來被廣泛應用于結構系統健康監測、模型校正、可靠性評估等領域［1］。貝葉斯模型更新是一種基于先驗信息和觀測數據校準模型的有效方法，其主要目的是結合代表工程師經驗判斷的先驗分布和代表觀測數據的似然函數，利用貝葉斯概率公理［2］，得到模型參數的后驗分布，從而減小模型的不確定性。設原系統模型輸入變量為X，則根據貝葉斯理論可以得到輸入變量X的后驗分布［3］為

式中：x為輸入變量X的樣本；s為觀測數據；fX(x|s)、fX(x)分別為輸入變量X的后驗和先驗分布密度函數；L(X|s)為似然函數。從式（1）中可以看出fX(x|s)的計算需要求解分母中的n重積分，通常難以求得解析解，因此人們研究并發展了大量求解該式的近似解法。文獻［4］首先采用Laplace 方法給出了積分的近似解，但是這種方法只適用于后驗分布概率密度函數在幾個孤立點處存在峰值的情況。近年來，隨著計算機性能的飛速發展，大量基于隨機過程模擬的抽樣方法被用來進行貝葉斯模型更新中后驗樣本分布的估計，其中發展迅猛且最為有效的是馬爾科夫鏈蒙特卡洛（Markov Chain Monte Carlo，MCMC）方法［5］。MCMC 方法通過模擬穩態分布為目標后驗分布的馬爾科夫鏈，來產生一組滿足后驗分布的相關樣本，從而利用樣本估計后驗統計信息。在MCMC 方法的基礎上，Beck 和Au［6］基于“ 拒絕采樣”思想提出Adaptive-Metropolis-Hastings 方法（AMH），采用核密度估計通過中間過程概率密度函數逐步逼近真實的后驗樣本的概率密度函數。對于高維問題，上述AMH 算法通常會得到大量重復樣本，抽樣效率很低。為了提高AMH 算法對高維問題的適用性，研究者相繼提出了過渡馬爾科夫鏈蒙特卡洛方法（Transitional Markov Chain Monte Carlo，TMCMC）［7］、混合蒙特卡洛方法（Hamiltonian Monte Carlo，HMC）［8］等有效地改善了AMH 算法對高維問題的適用性。然而，上述基于MCMC 發展的方法通常很難判斷何時馬爾可夫鏈已經漸進收斂于平穩分布且計算量較大［9-11］，因此一些學者提出了用于替代MCMC 的方法，如序列粒子濾波［12］、貝葉斯網絡框架（Bayesian Network，BN）［13］、貝葉斯近似計算（Approximate Bayesian Computation，ABC）［14］等方法，其中，Straub 和Papaioannou［15］于2015年提出了一種基于結構可靠性方法的貝葉斯模型更新（Bayesian Updating with structural Reliability，BUS）方法，這種方法基于簡單拒絕抽樣的思想，建立了貝葉斯更新與結構可靠度之間的橋梁，有效地將復雜貝葉斯更新中的高維積分問題轉化為一個典型的結構可靠性分析問題，進而采用可靠性分析方法來求解后驗樣本的分布，為貝葉斯模型更新問題開辟了一條新的求解思路。

然而，上述已有的方法都是在假設似然函數中的觀測值是準確測量的情況下進行的，即只考慮了輸入變量及其參數的不確定性。在工程實際獲取試驗數據的過程中，由于測量儀器的精度誤差，以及一些不可避免的人為因素帶來的誤差，導致觀測值不能準確測得，即觀測值也具有不確定性。確定性觀測值下貝葉斯模型更新的后驗分布參數是確定的，如后驗均值和后驗方差；而不確定性觀測值會導致貝葉斯更新輸出的后驗分布參數也具有不確定性，因此為了準確獲取后驗樣本的完整分布，就必須考慮觀測值在整個不確定性范圍內對貝葉斯模型更新后驗樣本分布的影響。文獻［16］基于MCMC 方法提出了一種觀測不確定性情況下的貝葉斯更新方法，但計算量比較大，而且MCMC 方法無法確保最終收斂到穩態分布。因此，本文基于BUS 方法建立觀測不確定性下的貝葉斯更新模型，充分考慮觀測值在整個不確定性范圍內對貝葉斯更新后驗樣本分布參數的影響，并提出單層Kriging、雙層Kriging 2 種模型求解的高效算法。

1 觀測不確定性下的貝葉斯更新

1.1 BUS 方法基本原理

考慮結構模型Y=g(X)，其中X=(X1，X2，…，Xn)為n維隨機輸入變量，如尺寸、材料性能、載荷等，其先驗分布為fX(x)；Y為模型輸出，如應力、應變、位移等；g(·)為輸入和輸出關系的模型。假設通過試驗或者測量得到輸出的一組觀測數據s=(s1，s2，…，sm)，在觀測數據s下輸入變量X的似然函數記為L(X|s)，其中第i個觀測值下的似然函數通常表示為第i個觀測值與模型輸出之間的偏差的概率密度函數［3］，即

為了解決式（1）中n重積分難以求解的問題，BUS 方法通過引入一個定義在［0，1］區間上均勻分布的輔助變量P，利用簡單拒絕抽樣方法來得到滿足后驗分布的樣本，從而將貝葉斯更新問題轉化為結構可靠性問題。將引入輔助變量P之后的增廣變量空間記為[X，P]，且增廣變量的聯合密度函數滿足fX，P(x，p)=fX(x)fP(p)，其中p為輔助變量P的樣本。為建立貝葉斯更新和結構可靠性分析之間的關系，定義新的失效區域Ω為

式中：c為一個和似然函數相關的正常數，使得對于任意的輸入變量X都有cL(X|s)≤1。基于式（3），可以得到一個可靠性問題的極限狀態方程：

因此，在BUS 方法中可得到后驗分布表達式［15］為

式中：I為指示函數，當h(X，P)≤0 時，I=1，反之，I=0。由式（5）可知，由先驗分布fX(x)產生且落入失效區域Ω中的樣本x將服從于后驗分布fX(x|s)。關于式（5）的詳細推導可參照文獻［15］。

由此可見，BUS 方法只需確定一個與似然函數相關的參數c，便可有效地將貝葉斯更新問題轉化為結構可靠性分析問題，從而使得常用的可靠性分析方法都可以用來進行貝葉斯更新，有效避免貝葉斯模型更新過程中高維積分難以求解的問題，因此，本文將BUS 方法進一步推廣到不精確觀測的情況。

1.2 觀測不確定性下的貝葉斯更新模型

觀測誤差是模型更新問題中最主要的不確定性因素之一，在結構的監測過程中，儀器精度、環境干擾等不確定性因素都會造成觀測數據失真，觀測誤差的存在導致似然函數存在不精確性，使得貝葉斯更新更加復雜。為此，本文借鑒BUS 方法，建立考慮觀測不確定性的貝葉斯更新模型。假設試驗中測量得到的m個輸出響應的觀測數據為s0=[s1，s2，…，sm]，由于環境因素，測量儀器精度等導致的相應的測量誤差為δ=[δ1，δ2，…，δm]，則真實的觀測數據S=[S1，S2，…Sm]將具有不確定性，并且存在于觀測數據與測量誤差組成的區間中，即Si∈[s0-δi，s0+δi] (i=1，2，…，m)。令則在觀測不確定性和輸入變量的隨機不確定性共同作用下第i個觀測的似然函數可以抽象為一個區間函數：

借助于BUS 方法的思想，引入一個定義在區間[0，1]上均勻分布的輔助變量P，則可將觀測區間不確定性和基本變量隨機不確定性共同作用下的貝葉斯更新問題轉化為區間和隨機變量共同作用下的可靠性分析問題。由于區間不確定性和隨機不確定性的共同作用，該可靠性分析問題的功能函數則為

式中：c1、c2為一組與似然函數相關的正常數，使得對于任意的輸入變量X都有而相應于式（8）中功能函數的失效域也不再單一，而是具有上下2 個邊界，即

以功能函數中含有2 個觀測變量為例，考慮觀測不確定性下的結構的功能函數及失效域如圖1 所示。

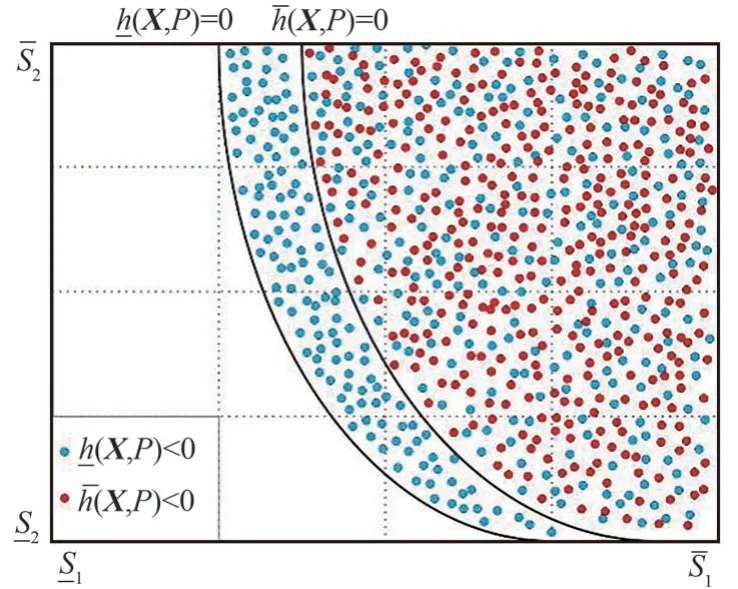
圖1 二維獨立觀測變量下功能函數及失效樣本分布Fig.1 Performance functions and corresponding failure domains in case of two-dimensional independent observation variables

基于此，可得到后驗分布的區間函數表示為

由式（7）～式（10）可知，本文借助于BUS 的思想，可以將觀測不確定性下的貝葉斯更新問題轉化為區間和隨機變量共同作用下的可靠性分析問題，進而建立觀測不確定性下的貝葉斯更新模型。所建模型表明，當考慮觀測不確定性時，輸入變量的后驗分布不再是單一的分布函數，而是一個區間函數，直接準確求解式（10）中的后驗分布區間函數通常需要大量的計算量。為了提高觀測不確定性下貝葉斯更新的效率，本文將建立觀測不確定性下貝葉斯更新的兩類基于Kriging 代理模型的算法。為了便于理解，第2 節簡單介紹Kriging 代理模型及建模方法。

2 Kriging 代理模型及建模方法

2.1 Kriging 代理模型的基本原理

Kriging 最初由南非采礦工程師Krige［17］于20 世紀50 年代提出，近年來發展為一類流行的統計學插值方法。作為一種插值模型，Kriging 預測結果為所有樣本點處模型響應的線性加權，且權重取決于訓練樣本點與預測樣本點之間的空間距離。相比于其他代理模型，Kriging 不僅能給出預測值，還能提供預測方差來衡量模型本身預測不確定性［18］。Kriging 模型可以表示為隨機分布函數和多項式之和［19］：

式中：gK(X)為未知的Kriging 模型；φT(X)=[φ1(X)，φ2(X)，…，φp(X)]為n維隨機向量X的回歸基函數；p為基函數的個數；β=[β1，β2，…，βp]T為基函數的最小二乘回歸系數；φT(X)β為由基函數組成的線性回歸項，代表隨機過程中均值的偏移，用來擬合模型的整體趨勢；Z(X)為均值為0、方差為σ2的高斯過程，其協方差矩陣表示為

式中：σ2為高斯過程方差；R(x(i)，x(j))為任意2 個輸入樣本之間的相關函數，其為相關矩陣R的分量，i，j=1，2，…，m0；m0為訓練樣本集中數據個數。R(x(i)，x(j))在大多數工程問題中都采用高斯型相關函數，計算公式為

由廣義最小二乘回歸方法可以得到Kriging模型在未知點x處的預測值gK(x)為

最優相關參數d=[d1，d2，…，dn]T可通過求極大似然估計的最大值得到，即

2.2 交叉驗證方法

假設K折交叉驗證中，初始訓練樣本集D{x，y} 由M個輸入輸出對 (x(i)，y(i)) (i=1，2，…，M)組成，其中y(i)為訓練樣本點x(i)的響應值。首先將D分成K個大小相似的互斥子集，即，然后，使用K-1 個子樣本集構造Kriging 代理模型，剩余的子樣本集作為測試樣本用來計算代理模型的誤差，將該過程重復K次，直到每個子樣本集都被作為測試樣本使用過一次。由此得到K×1 交叉驗證誤差向量ecv和K×1 預測方差向量可分別表示為

圖2 10 折交叉驗證示意圖［21］Fig.2 Schematic diagram of 10-fold cross validation［21］

通過交叉驗證方法，均方根誤差的計算公式為

誤差相關系數為

3 考慮觀測不確定性的貝葉斯更新算法

BUS 方法的有效性依賴于正常數c的選取，c的取值需要使得任意的先驗分布樣本都滿足cL(X|S)≤1。因此c的最優值定義為1/max(L(X|S))［3］。一方面，c取值過大會導致由簡單拒絕抽樣得到的樣本并不全滿足后驗分布，降低了BUS 方法的準確性；另一方面，c取值過小將會導致得到滿足后驗分布的后驗樣本很少，降低了BUS 方法的計算效率。因此BUS 方法的關鍵在于常數c的確定，但是對于大多數似然函數，特別是存在多個觀測值的貝葉斯更新問題，c的值通常無法解析計算，而數值計算c的過程中需要大量調用原始模型。當考慮觀測不確定性時，需要在不同觀測值處重復計算常數c，這一過程需要大量調用原始模型，對于大型復雜結構有限元模型計算成本巨大，觀測不確定性下的貝葉斯模型更新帶來了新的挑戰。因此，本文引入Kriging 模型，建立求解觀測不確定性下貝葉斯更新模型的單層Kriging 和雙層Kriging 算法，有效地提高觀測不確定性下貝葉斯模型更新的計算效率。

3.1 雙層Kriging 算法

雙層Kriging 算法的基本思想是借助似然函數中觀測區間不確定性與基本變量隨機不確定性可以分離的特點，建立原始模型的帶交叉驗證的Kriging 模型，并代入原似然函數得到代理似然函數。然后基于代理似然函數，通過歷遍觀測變量取值區間的方法，得到式（7）中的區間似然函數與式（8）中的區間功能函數的上下邊界，并結合Monte Carlo 模擬（MCS）方法求解式（10）得到相應的后驗分布區間，具體的計算步驟如下。

步驟1將n維輸入變量X增廣為n+1 維X+=[X，P]，并根據X的聯合概率密度函數fX(x)產生X+前n維容量為N的樣本池Q={x(1)，x(2)，…，x(N)}，作為更新Kriging 代理模型和貝葉斯更新的樣本池；1 維輔助變量P的容量為N的樣本池P={p(1)，p(2)，…，p(N)}由［0，1］區間上的均勻分布概率密度函數隨機產生。

步驟2在樣本池Q中抽取前M（M?N）個樣本x(o)(o=1，2，…，M)，代入原模型g(X)，計算相應的功能函數值g(x(o))(o=1，2，…，M)，由這M個輸入輸出樣本對構成初始訓練樣本集D={(x(1)，g(x(1)))，(x(2)，g(x(2)))，…，(x(M)，g(x(M)))}。

步驟3將D分成大致相等的K份子樣本集，然后使用K-1 個子樣本集構造原始功能函數的Kriging 代理模型，剩余的子樣本集作為測試樣本用來計算代理模型的誤差，將該過程重復K次，直到每個樣本集都被作為測試樣本使用過1 次，由此得到交叉驗證的誤差向量ecv。

步驟4根據式（22）計算交叉驗證的均方根誤差RMSEcv，當RMSEcv≤0.05 時停止交叉驗證過程，執行步驟6。若RMSEcv＞0.05，則需在訓練樣本集D中繼續增加Kriging 建模輸入輸出樣本對，執行步驟5。

步驟5在樣本池Q中抽取第M+1 至第M+M/K個樣本，M+2，…，M+M/K)，計算相應的功能函數值構成補充訓練樣本集將補充訓練樣本集D+并入訓練樣本集D，即M+M/K，再令M=M1，返回步驟3 更新Kriging模型。

步驟6采用當前Kriging 模型gK(X)替代原模型g(X)，得到代理似然函數L(X|S)=

步驟7在觀測區間[s0-δi，s0+δi] (i=1，2，…，m)上由均勻分布概率密度函數隨機產生m維容量為l的觀測樣本池S={s(1)，s(2)，…，s(l)}，作為構建區間似然函數的觀測值樣本池。

步驟8將觀測樣本池S中的第j(j=1，2，…，l)個觀測樣本和樣本池Q中變量X的N個樣本Q={x(1)，x(2)，…，x(N)}代入代理似然函數，計算得到第j個觀測樣本對應的N個代理似然函數值并求得代理似然函數的最大值，取cj=1/max(L(x(r)|s(j))) (r=1，2，…，N)。

步驟9將步驟8中得到的N個代理似然函數值和增廣變量X+的第n+1維輔助變量P的N個樣本P={p(1)，p(2)，…，p(N)}一起代入極限狀態方程hj(X，P)=P-cj L(X|S)，計算得到第j個觀測樣本對應的N個極限狀態函數值hj(x(r)，p(r))(r=1，2，…，N)，求得滿足hj(x(r)，p(r))≤0(r=1，2，…，N)的所有后驗樣本并計算后驗樣本的均值和標準差

步驟10若j＜l則令j=j+1，返回步驟8，從觀測值樣本池S中抽取下一個觀測樣本，計算新的觀測樣本下的后驗分布；若j≥l則結束貝葉斯更新，執行步驟11。

步驟11將求得的l組后驗樣本的均值及標準差按次序統計量排序，取得其最大值和最小值作為最終后驗樣本分布參數的區間端點，即后驗樣本均值標準差

雙層Kriging 算法通過外層歷遍觀測區間和內層構建原始功能函數的代理模型的方式，可以精確地給出后驗分布參數的取值區間，適用于對后驗分布參數精度要求較高的觀測不確定性下的貝葉斯模型更新問題。但其由于采用雙層計算框架，一般計算量較大，計算效率不高。在觀測不確定性下的貝葉斯更新過程中，有時不需要很精確地得到后驗樣本分布參數的區間，而只需要求得后驗分布參數的平均估計即可對原模型進行校正，為此，本文建立了帶交叉驗證的單層Kriging 算法。

3.2 單層Kriging 算法

單層Kriging 算法的基本思想是將觀測變量看作觀測區間中的均勻分布變量，進而直接建立反映似然函數與觀測變量和基本隨機變量之間關系的帶交叉驗證的Kriging 模型。然后基于代理似然函數，結合MCS 方法得到相應的平均后驗分布，具體的計算步驟如下。

步驟1將n維輸入變量X增廣為n+1+m維X+=[X，P，S]，并根據X的聯合概率密度函數隨機產生n維輸入變量X的容量為N的樣本池Q={x(1)，x(2)，…，x(N)}，Q作為更新Kriging 代理模型和貝葉斯更新的樣本池；1 維輔助變量P的容量為N的樣本池P={p(1)，p(2)，…，p(N)}由區間［0，1］上的均勻分布概率密度函數隨機產生；m維觀測變量S的容量為N的樣本池S={s(1)，s(2)，…，s(N)}由觀測區間[s0-δi，s0+δi](i=1，2，…，m)上均勻分布概率密度函數隨機產生，S作為構建似然函數的觀測值樣本池。

步驟2在樣本池Q中抽取前M（M?N）個樣本x(o)(o=1，2，…，M)，代入原模型g(X)，計算得到相應的功能函數值g(x(o))(o=1，2，…，M)；在觀測樣本池S中抽取前M個觀測樣本s(o)(o=1，2，…，M)。將g(x(o))(o=1，2，…，M)、s(o)(o=1，2，…，M)代入似然函數，計算相應的似然函數值將M對輸入樣本(x(o)，s(o))(o=1，2，…，M) 和輸出樣本L(x(o)|s(o))(o=1，2，…，M)構成初始訓練樣本集

步驟3將D分成大致相等的K份子樣本集，然后使用K-1 個子樣本集構造似然函數的Kriging 代理模型，剩余的子樣本集作為測試樣本用來計算代理模型的誤差，將該過程重復K次，直到每個樣本集都被作為測試樣本使用過1 次，由此得到交叉驗證的誤差向量ecv。

步驟4根據式（22）計算交叉驗證的均方根誤差RMSEcv，當RMSEcv≤0.05 時停止交叉驗證過程，執行步驟6。若RMSEcv＞0.05，則需在集合D中繼續增加Kriging 建模輸入輸出樣本對，執行步驟5。

步驟5在樣本池Q中抽取第M+1 至第M+M/K個樣本x(o+)(o+=M+1，M+2，…，M+M/K)，計算相應的功能函數值g(x(o+))(o+=M+1，M+2，…，M+K)；在觀測樣本池S中抽取第M+1 至第M+M/K個觀測樣本s(o+)(o+=M+1，M+2，…，M+M/K)，將功能函數值和觀測樣本代入似然函數計算相應的似然函數值(o+=M+1，M+2，…，M+M/K)構成補充訓練樣本集將補充訓練樣本集D+并入訓練樣本集D，即D=D+D+={(x(o)，L(x(o)|s(o)))} (o=1，2，…，M+M/K)，令M1=M+M/K，再令M=M1，返回到步驟3 更新Kriging 模型。

步驟6采用當前Kriging 模型替代原似然函數L(X|S)，得到代理似然函數LK(X|S)。

步驟7將輸入變量X的N個樣本Q={x(1)，x(2)，…，x(N)}及觀測變量S的N個樣本S={s(1)，s(2)，…，s(N)}代入代理似然函數LK(X|S)，計算得到N個代理似然函數值LK(x(r)|s(r))(r=1，2，…，N)，并求得代理似然函數的最大值，取

步驟8將輔助變量P的N個樣本P={p(1)，p(2)，…，p(N)}、步驟7 中得到的N個代理似然函數值LK(x(r)|s(r))(r=1，2，…，N)、常數c代入極限狀態方程h(X，P)=P-cL(X|S)，計算得到N個觀測樣本對應的極限狀態函數值h(x(r)，p(r))(r=1，2，…，N)，求得滿足h(x(r)，p(r))≤0(r=1，2，…，N)的所有后驗樣本xh，并計算后驗樣本xh的均值μh和標準差σh。

單層Kriging 算法通過將觀測變量看作觀測區間中均勻分布的隨機變量，進而直接建立起似然函數與觀測變量和基本隨機變量的Kriging 代理模型，可以給出后驗分布參數的平均估計，計算效率較高，適用于對后驗分布參數精度要求不高的觀測不確定性下的貝葉斯更新問題。

4 算例

本節用3 個觀測不確定性下的貝葉斯模型更新問題，驗證本文所建觀測不確定性下的貝葉斯更新模型對于降低輸入變量分布參數不確定性的有效性，以及所提2 種算法對于后驗樣本分布參數計算的準確性和高效性。對于每個算例，本文采用直接的MCS 方法作為對比參考方法，通過將各算法執行30 次運算得到后驗方差的變異系數來判斷算法是否收斂。

4.1 一維線性數值模型

算例4.1 采用一個具有解析后驗分布的例子來驗證本文方法的準確性和可靠性。考慮一維線性數值模型g(X)=X，其中X的先驗分布fX(x)是均值為μ、標準差為σ的正態分布，似然函數L(X|s)是均值為S、標準差為σε的正態分布，先驗概率分布和似然函數之間滿足共軛關系。在這種情況下，X的后驗概率分布仍為正態分布，并且具有解析表達式。假設可以得到變量X的ns組觀測數據si，則X的后驗均值μh和標準差σh的解析表達式［22］為

在本算例中，考慮X的5組觀測數據分別為0.5、0.6、-0.4、0.3、0.2，觀測誤差均為0.05，故觀測變量：S1∈[0.45，0.55]、S2∈[0.55，0.65]、S3∈[-0.45，-0.35]、S4∈[0.25，0.35]、S5∈[0.15，0.25]。因此本例的似然函數表示為

式中：σε為試驗中觀測誤差的標準差，取σε=1。本例輸入變量的先驗分布取為標準正態分布，即X～N(0，1)。利用上述似然函數可以對輸入變量進行貝葉斯更新。

本算例需更新線性系統的一維輸入變量，采用本文所提2 種算法以及2 種MCS 對照方法分別進行計算，結果如表1 所示，其中雙層MCS 算法表示在每一個觀測樣本值處，都采用MCS 方法求解式（4）中的可靠性分析問題，得到相應的后驗分布參數，進而通過歷遍觀測區間的方式得到后驗分布參數區間。單層MCS 算法表示將觀測變量看作觀測區間中的均勻隨機變量，由MCS 方法求解式（4）中的可靠性分析問題，即可得到滿足條件的后驗分布樣本。本例中輸入變量先驗分布和似然函數滿足共軛關系，因此可由式（24）在每一組觀測樣本處解析求得精確后驗分布參數，用來對比驗證本文算法對后驗樣本分布求解的可行性和準確性。

表1 輸入變量X 后驗分布參數Table 1 Posterior distribution parameters of input variables X

從表1 中數據可以看到，4 種方法所得到的后驗分布參數均收斂至標準精確解析解，驗證了本文所提算法框架的可行性和準確性。

圖3 給出了各種方法計算得到的輸入變量的后驗分布及先驗分布圖。其中，精確解析解為觀測值取均值（即不考慮觀測不確定性）時由式（24）計算得到的標準解析解，PDF 為概率密度函數，從圖3 中可以看出，4 種方法計算得到的后驗分布概率密度曲線均收斂至標準解析解。與不考慮觀測不確定性的精確解析解相比，當考慮觀測不確定性時，貝葉斯更新后的輸入變量后驗分布不再是確定的單一函數而是一組區間分布函數，雙層算法可以得到完整的后驗分布概率密度曲線族，形成后驗分布域，而單層算法可以得到平均后驗分布曲線，并且與精確解析解吻合很好。另外，通過對比圖3 中變量先驗概率分布和后驗概率分布可以發現，相比于先驗概率分布，經過貝葉斯更新后變量的后驗概率分布發生改變，主要變化體現在后驗分布概率密度函數曲線更集中、分散性更小，這表明該線性系統輸入變量分布參數的不確定性得到有效降低，證明了所提算法的有效性。

圖3 數值模型輸入變量先驗及后驗分布Fig.3 Prior and posterior distribution of numerical model input variables

4.2 懸臂梁結構

某矩形截面懸臂梁如圖4 所示，其受到水平、豎直方向的載荷X、Y的作用，以其自由端位移不超過D0為約束建立功能函數為

圖4 懸臂梁結構圖Fig.4 Structure diagram of cantilever beam

式中：S1、S2為在準確后驗分布參數下觀測得到的位移，由位移觀測數據及觀測誤差可得到S1∈[0.69，0.72]、S2∈[0.68，0.71]；σε1、σε2分別為2 次獨立試驗中位移觀測誤差的標準差，取σε1=σε2=0.03。本例考慮的先驗分布參數如表2所示。

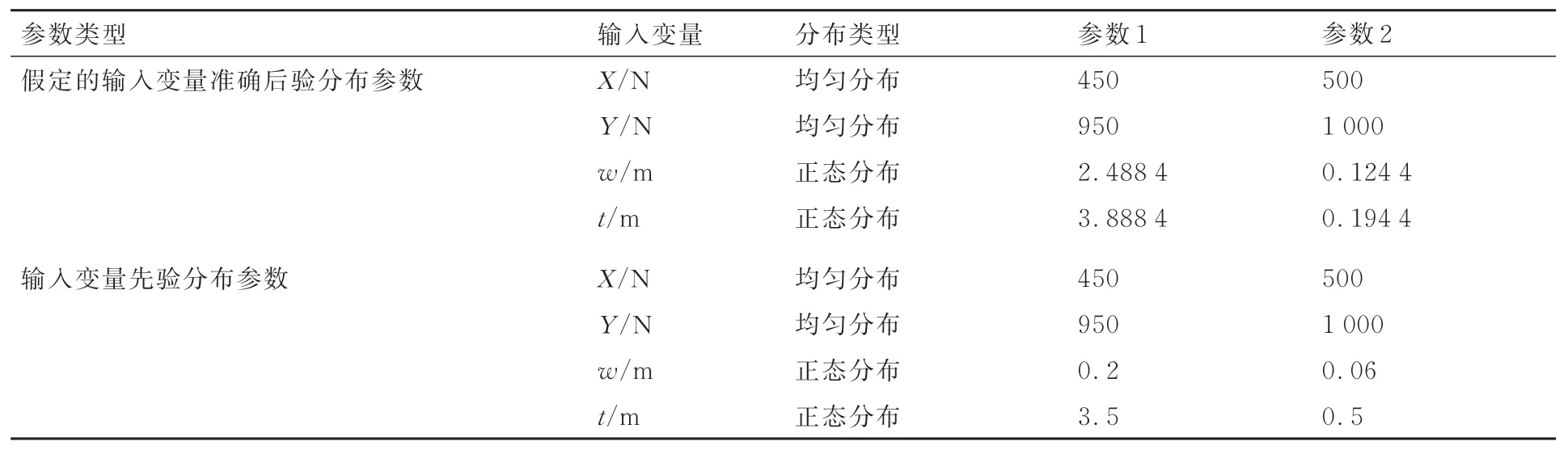
表2 矩形截面懸臂梁結構輸入變量假定的后驗分布參數及先驗分布參數Table 2 Assumed posterior distribution parameters and prior distribution parameters of input variables for rectangular cross-section cantilever beam structure

表3 給出了觀測樣本為50 時該懸臂梁結構模型經過貝葉斯更新后輸入變量的后驗分布參數。結果表明4 種方法計算得到的后驗分布參數與準確解均吻合得很好。圖5 中進一步給出了在50 個觀測樣本下4 種方法計算得到的后驗分布與準確后驗分布的對比圖，進一步證明了本文方法得到的完整后驗分布與準確解也吻合得很好，其中雙層算法可以得到完整的后驗分布族，而單層算法可以得到后驗分布的平均值，與不考慮觀測不確定性的準確解更為接近。圖5 同時給出了在觀測區間內不同觀測樣本量下單層MCS 方法計算得到的后驗分布與標準后驗分布的對比。

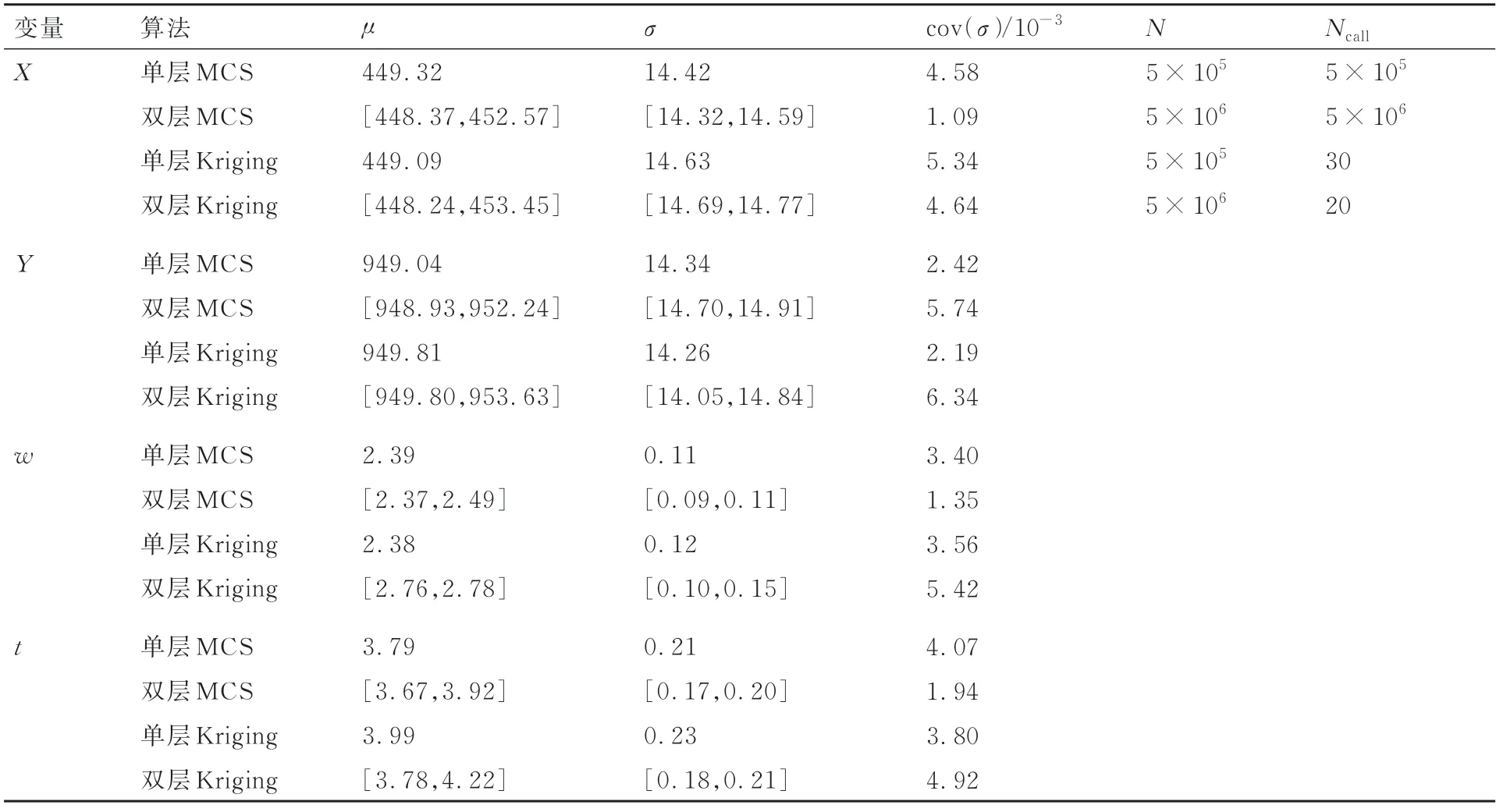
表3 矩形截面懸臂梁結構輸入變量后驗分布參數（50 個觀測樣本）Table 3 Posterior distribution parameters of input variables for rectangular cross-section cantilever beam structure（50 observed samples）

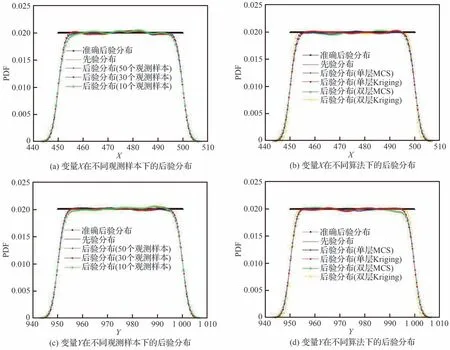
圖5 懸臂梁結構輸入變量先驗及后驗分布Fig.5 Prior and posterior distribution of input variables for cantilever beam structure

可以看出，對于變量X、Y，在不同觀測樣本量下，經過貝葉斯更新得到的后驗分布參數與先驗分布參數相比變化很小，這表明在先驗分布極為準確的情況下，經過本文貝葉斯更新模型所得到的后驗分布幾乎不變，與準確的后驗分布保持一致；對于先驗分布很不準確且分散性很小的變量w，隨著觀測樣本量的增加，經過本文貝葉斯更新模型所得到的后驗分布逐漸收斂于準確分布，后驗均值逐漸增大收斂于準確的后驗均值，后驗方差逐漸增大更接近于準確的后驗方差；對于先驗分布不準確且分散性較大的變量t，經過貝葉斯更新后的均值收斂于準確后驗均值，后驗分布概率密度函數曲線更為集中、分散性更小接近真實值。證明了本文貝葉斯更新模型對于提高觀測不確定性下的模型準確性。

對于該顯式功能函數算例，利用單層MCS方法，需要調用功能函數5×105次得到收斂的后驗樣本，而單層Kriging 方法由于使用了代理模型，僅需要調用30 次功能函數便可得到收斂的后驗樣本。雙層MCS 方法由于需要在外層歷遍觀測區間，需要更大的計算量，調用功能函數5×106次，同樣，雙層Kriging 算法由于使用代理模型僅需要調用20 次功能函數。單層Kriging 算法由于直接建立起似然函數與觀測變量和基本隨機變量的代理模型，其變量維度比雙層Kriging 算法更高，為保證模型精度，需要更多建模樣本對來訓練Kriging 模型，因此單層Kriging 算法調用原始功能函數次數比雙層Kriging 算法要高，但單層Kriging 算法相比于雙層Kriging 算法需要更小的樣本池，對于功能函數計算時間可以忽略的顯示功能函數，計算耗時一般會更短。

4.3 機翼結構

機翼結構是飛機的重要部件之一，安裝在機身上，其最主要作用是產生升力，與尾翼一起形成良好的穩定性與操作性。另外可以在機翼內部裝載彈藥、設備和油箱，在機翼上可以安裝起落架、發動機、懸掛導彈、副油箱及其他外掛設備。本節主要研究一個簡化的機翼模型，該機翼模型主要由桁條、翼肋、翼墻、蒙皮組成。通過ANSYS 有限元分析軟件對該簡化的機翼模型進行靜力學分析。在該有限元模型建模過程中，桁條采用桿單元結構，其中橫截面積為A、彈性模量為E1。翼肋和翼墻采用板單元結構，其中彈性模量為E2、厚度為θ2。蒙皮也同樣采用板單元結構，其中彈性模量為E1、厚度為θ1。以上單元材料泊松比均為0.3。該機翼幾何外形及其所受外載荷如圖6 所示，該機翼中由桿板結構形成的一個封閉盒段的長度為L。此外，由于機翼主要的受力形式為分布力和集中力，因此在本例中假設該機翼模型受到的所有外載荷最終都近似為集中力，且載荷大小為P，如圖6（a）所示。假設以上輸入隨機變量均服從正態分布，且其分布參數如表4 所示。對于該機翼模型進行有限元分析，可建立如圖6（b）所示的機翼有限元模型，ANSYS靜力學分析得到該機翼在Y方向上的位移云圖，如圖6（c）所示。將Y方向上的位移閾值設置為U0=0.2 m，若該機翼模型在Y方向上的最大位移超過0.2 m，則可認為該機翼模型發生失效，反之，則認為該機翼模型安全。將有限元模型計算得到的Y方向的最大位移U(A，E1，E2，θ1，θ2，P，L)作為模型的輸出，以Y方向最大位移不超過U0為約束建立功能函數為g(A，E1，E2，θ1，θ2，P，L)=0.2-|U(A，E1，E2，|θ1，θ2，P，L)，可以定義似然函數L=(A，E1，E2，)θ1，θ2，P，L|S為

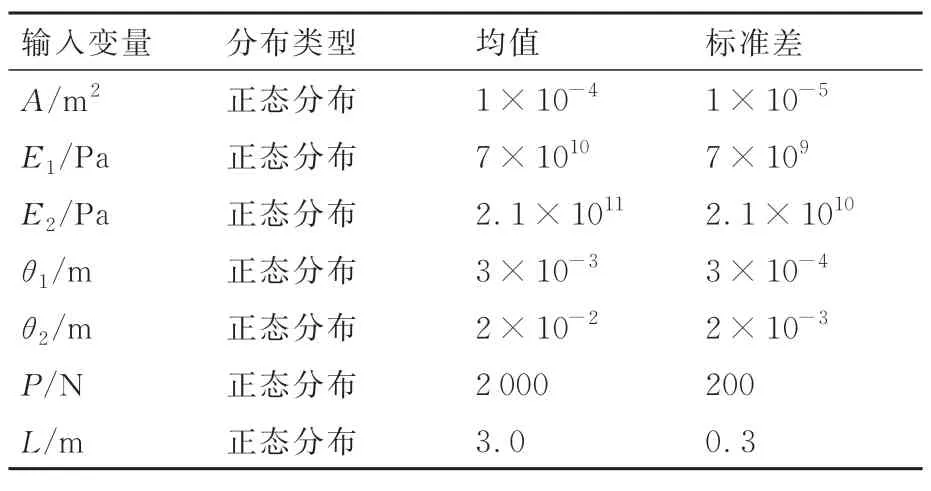
表4 飛機機翼有限元模型的輸入變量先驗分布參數Table 4 Prior distribution parameters of input variables for finite element model of aircraft wing

圖6 機翼結構有限元模型圖Fig.6 Finite element model diagram of wing structure

式中：S1為觀測變量，由試驗中對機翼Y方向最大位移觀測得到，由機翼位移觀測數據及其觀測誤差可得到S1∈[0.03，0.08]；σε1為位移觀測誤差的標準差，取σε1=0.01。

表5 給出了該機翼結構模型經過貝葉斯更新后輸入變量的分布參數，從表中數據可以看到，利用單層MCS 方法，需要調用有限元模型3.2×104次才能得到收斂的后驗樣本，而單層Kriging方法，僅需要調用327 次功能函數便可得到收斂的后驗樣本。雙層MCS 方法需要調用功能函數3.2×105次，而雙層Kriging 算法僅需要調用268次有限元模型。2 種代理模型算法均大幅減少了有限元模型的調用次數，極大地縮短了計算耗時，提高了計算效率。

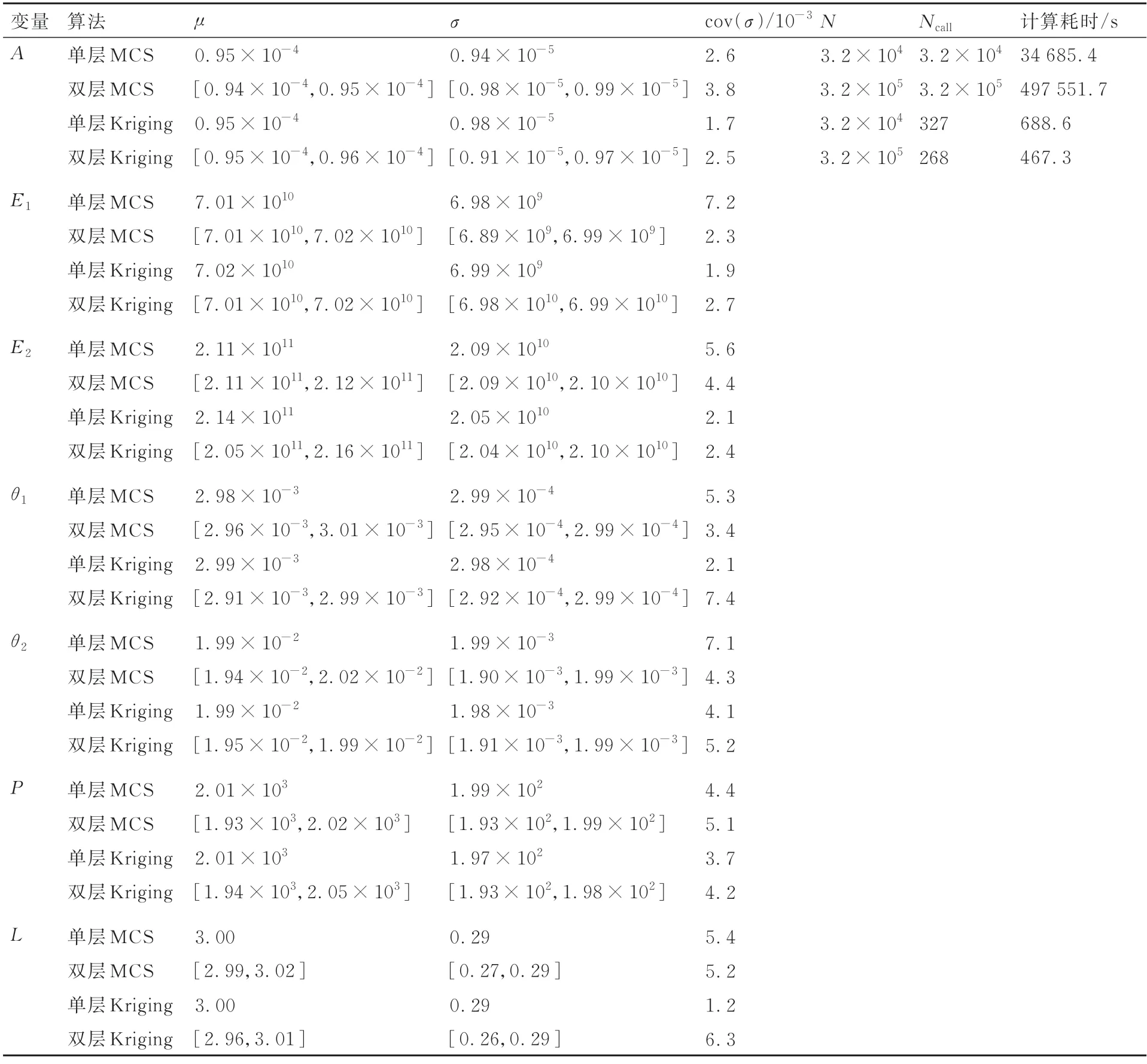
表5 飛機機翼結構輸入變量后驗分布參數Table 5 Posterior distribution parameters of input variables for aircraft wing structure

圖7 給出了各種方法得到的機翼結構有限元模型輸入變量的后驗分布和先驗分布圖，從圖7 中可以看出，4 種方法計算得到的后驗樣本分布基本一致，通過對比MCS 方法可以得到，本文所提的單層Kriging 及雙層Kriging 算法均能夠準確計算得到后驗樣本分布；通過對比圖7 中各變量先驗概率分布和后驗概率分布可以發現，除了機翼截面積A，其他變量的后驗概率分布相比于先驗概率分布變化均不大，這表明這些變量的先驗分布較為準確。截面積A的后驗概率分布相比于先驗概率分布變化較大，除了均值的移動外，后驗分布概率密度函數曲線分散性也更小，這表明該機翼結構截面積A的先驗分布不準確，經過貝葉斯更新后分布參數的不確定性得到降低。本例證明了所提方法應用在工程結構大型有限元模型貝葉斯更新過程中的高效性和準確性，具有一定的工程指導意義。

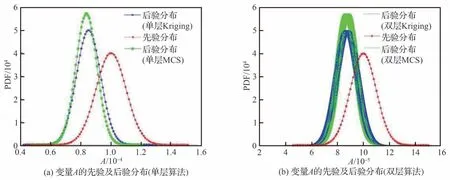
圖7 飛機機翼結構輸入變量先驗及后驗分布Fig.7 Prior and posterior distribution of input variables for aircraft wing structure

5 結論

針對已有貝葉斯更新方法無法考慮實際中存在的觀測不確定性問題，建立了觀測不確定性下的貝葉斯更新模型，并提出了模型求解的兩種高效算法。3 個算例結果表明，所建貝葉斯更新模型通過將觀測不確定性情況下的貝葉斯更新問題轉化為區間和隨機變量共同作用下的可靠性分析問題，能夠充分考慮觀測中實際存在的不確定性和基本變量的隨機不確定性，對輸入變量的先驗分布參數進行有效的校正。所發展的2 類算法通過Kriging 模型能夠在保證精度的同時大幅提高觀測不確定性下貝葉斯模型更新的效率。雙層Kriging 算法可以精確地得到后驗分布參數的取值區間，單層Kriging 算法可以高效地給出后驗分布參數的平均估計，并且2 種算法都能夠給出輸入變量準確完整的后驗分布。所建更新模型及其求解的2 類算法實現了觀測不確定性下貝葉斯模型更新的量化估計。需要說明的是，由于本文所提算法直接采用MCS 抽樣使得樣本池規模較大，影響了觀測不確定性下貝葉斯模型更新的效率，可采用一些高效的抽樣方法如重要抽樣方法等進一步縮減樣本池規模，提高算法的計算效率和穩健性。