基于密度和粒子群的SVM 算法研究?
唐 瀛 閆仁武
(江蘇科技大學計算機學院 鎮江 212028)
1 引言
在1995 年時Vapnik 和Cortes 領導的AT&Bell實驗室[1]正式提出了支持向量機(SVM)算法[2]。支持向量機在對數據進行分類時通過結構風險最小化原則尋找超平面從而進行分類,并且它能夠將低維的不可分特征向量通過使用核函數映射,從而轉換到高維特征空間,進而進行分類,這樣在實際的機器學習問題中能夠得到應用[3]。由于SVM 算法在訓練樣本的訓練階段進行超平面劃分過程中會出現設置不準確的情況,本文提出使用基于密度的裁剪方法對訓練樣本進行裁剪,去除樣本集的噪聲和冗余樣本,優化分類超平面的劃分。因為懲罰因子C 和核函數g對于分類性能影響較大[4],提出基于粒子群算法對SVM算法進行改進,通過粒子群算法優化懲罰因子C和核參數g,提高SVM分類準確率。
2 支持向量機(SVM)算法
支持向量機實質是一種分類算法,能夠解決在樣本集中兩類樣本分類問題,通過尋找一個最優超平面使得對兩類樣本的分割間隔達到最大,從而將樣本集按照規則進行分類。
1)線性可分支持向量機原理
假設訓練樣本集為(xi,yi)(i=1,2…,m),其中xi?Rn為輸入變量,yi是對應的預期值,m 是樣本的數量,在線性回歸[5~6]的情況下,利用SVM構造一個目標函數,可獲得最優分割超平面的函數為
式中:ω?Rn為權值矢量,b ?R 為偏差量,對于需要分類的兩類樣本來說,它們之間的距離為此時為了使分類效果最優,則需要讓兩類樣本距離最大,所以相當于求||ω||的最小值。那么求權值ω和偏差b就可以通過下面的求解最優問題來解決:
引入拉格朗日[7]公式,然后再根據轉換后的問題求解,從而獲取最優解:
在式(4)中取得最優解后,于是將a的最優解設為a*,把最優解a*代入下列公式,并求出關于分類面的分類器閾值b*以及全系數向量ω*:
對于取得的值b*和ω*,將其代入下列公式當中,形成分類決策的超平面形式化方程:
再通過將樣本轉化的數據代入最后的方程中進行分類,得到分類結果。
2)線性不可分支持向量機原理
在目前日常生活中我們遇到的問題很多都是線性不可分問題,在線性不可分的情況下,使用SVM 算法進行分類時會通過引入一個松弛變量δi,然后在松弛變量前加入一個懲罰系數C,通過將懲罰系數C 的變化來控制分類錯誤的數量,然后通過下面的求解最優問題來解決:
式中:C 為懲罰因子,δi為松弛變量,當C 取值大時表示對分類的懲罰力度大。使用拉格朗日函數和核函數后可獲得線性回歸函數:
式中:αi為拉格朗日參數,K(xi,yi)為核函數。
本文采用高斯核函數來映射數據并求取最優分類面,高斯核函數的計算公式為
3 改進支持向量機算法
3.1 基于密度的訓練樣本裁剪方法算法原理
為了衡量樣本分類密度,實現對于訓練樣本的裁剪,接下來給出關于裁剪算法的相關定義:
定義1設樣本集中樣本X 與樣本Y 之間的距離為Dis(tX,Y),定義X的ε鄰域為
定義2設定樣本集M=C1∪C2∪C3∪C4∪…Cm(i=1,2…,m)代表一個樣本類別,且Ci∩Cj=?(i,j=1,2…,m),對于任意的X?Ci,若X 的ε鄰域內任何樣本都屬于Ci,則X 在類內區域,否則,X 在類邊界區域。
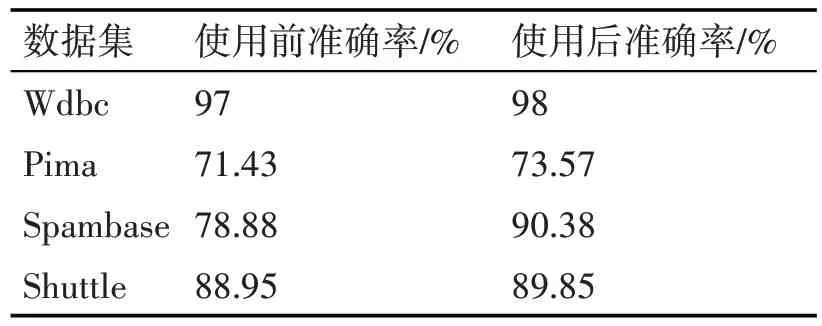
定義3給定樣本閾值Minpts(Minpts>0,Minpts?Z),那么對于任意的樣本X,若X 的ε鄰域中存在的樣本數|Nε(X)|>Minpts時,則X 處于高密度區域,若X 的ε鄰域中存在的樣本數|Nε(X)|=Minpts時,則X 處于均勻密度區域,若X 的ε鄰域中存在的樣本數|Nε(X)| 定義4給定鄰域半徑ε和樣本閾值Minpts(Minpts>0,Minpts?Z)。對于任意的樣本X 和X 鄰域內的樣本Y,若|Nε(Y)|>Minpts,則Y處于高密度區域,且Y 與X 高密度可達;此時把所有高密度可達的樣本Y 的樣本集定義為RH(X),同理把所有均勻密度可達的樣本Y 的樣本集定義為RA(X),把所有低密度可達的樣本Y的樣本集定義為RL(X)。 基于密度的訓練樣本裁剪方法[8]原理如下: 1)類邊界區域樣本裁剪如圖1所示: 圖1 類邊界樣本裁剪示意圖 設定Minpts=4,在圖中三個圓形分別是對于樣本A、B、C鄰域ε的區域,圖中分為兩種類別的樣本1 和樣本2,此時樣本B 處于類邊界區域,且樣本B的ε鄰域內樣本數量超過Minpts,是一個高密度區域樣本,所以會對樣本B 進行裁剪,根據上述定義,樣本A 則會被裁減掉,且位于樣本B 的ε鄰域中的其他三個類別樣本為1 的樣本,而樣本C 的ε鄰域中的樣本數量沒有超過Minpts,則不會對其鄰域進行裁剪,在裁剪后,樣本B 會處于均勻密度區域,同時能夠降低類別樣本1對測試樣本X(未知類別)的干擾,提高準確率。 2)在對于類內區域樣本進行裁剪時,則會裁減掉更多的冗余樣本,此時需要設置一個最少樣本閾值lowpts(lowpts>0,lowpts ?Z),且lowpts ≤Minpts,如果類內樣本X的鄰域內樣本數量|Nε(X)|>lowpts,將與X 高密度可達的樣本進行裁剪,直到|Nε(X)|=lowpts 時停止;當|Nε(X)|≤lowpts時,則將X 的ε鄰域內所有訓練樣本進行保留。 基于密度的訓練樣本裁剪方法具體算法如下: 第一步我們首先需要把樣本集X 中處于類內區域且鄰域半徑ε中樣本數量少于Minpts 的低密度區域樣本添加到我們新建的樣本集W中,然后對樣本集X 進行篩選,若樣本集中X[i]的鄰域半徑ε內樣本數量小于Minpts,則保留。 通過這樣處理之后就能得到低密度區域的樣本集W和高密度樣本集WH,接下來進行第二步: 在第二步中我們首先一次遍歷樣本X,對每個樣本X[i]獲取它的鄰域半徑內樣本集,此樣本集會包含|Nε(X)|>lowpts 的樣本,然后將這個樣本集與低密度樣本集Z 取差值,并添加到樣本集Y 中,因為每次遍歷都會去除樣本集Y 中低密度樣本,只有高密度樣本,而且排除了|Nε(X)| 在實際密度裁剪算法中的參數鄰域半徑ε、Minpts 和lowpts 的具體值會直接影響到裁剪效果,并且這幾種參數值當中具有某種關聯,而在這三種值當中,lowpts的值由Minpts間接決定,于是給出以下關于密度裁剪算法參數確定的定義: 定義5:給定訓練樣本集M,把訓練樣本集M中的樣本距離訓練樣本集M 中的樣本X 第k 近的樣本,與樣本X 之間的距離設為Distk(X),于是當訓練樣本集M 的最少樣本數為Minpts時,樣本集M 的平均鄰域半徑為 通過以上定義,在對參數鄰域半徑ε、Minpts和lowpts 的進行多次設定實驗便能得到測試結果。從而可以得到參數設定的經驗值[9],當Minpts的值設置為訓練樣本的平均樣本數的5%~8%,lowpts 的值設置為Minpts 的0.7~0.8 倍,此時的裁剪效果最好。 粒子群算法[10-11]實質是基于模擬鳥群覓食過程而提出的一種尋優算法。研究人員Eberhart 和Kennedy 發現鳥群在覓食過程中如果發現草坪上某處有面包[12],然后整個鳥群通過信息共享調整位置移動到面包地吃到面包。于是模擬鳥群的移動過程提出了粒子群算法,通過距離速度計算和個體鳥與群體鳥的信息共享[13],然后找到調整整個鳥群所有鳥的位置的最優解,不斷更新整個鳥群的位置,最終達到尋優目標[14]。粒子群算法選擇精度和速度優良,在數據挖掘方向使用較多,對于算法的參數尋優方向也有大量使用。 假設尋優問題[15]的空間維度為N,尋優問題的種群大小為M,組成的初始種群為Xi={X1,X2,…,Xm},則第i個粒子在某一時刻的位置和速度分別為Xi(t)=[Xi1(t),Xi2(t),…,Xin(t)]和Vi(t)=[Vi1(t),Vi2(t),…。Vin(t)],粒子的最優位置為pbesti(t)=[Pi1(t),Pi2(t),…。Pin(t)],粒子的最優位置為gbesti(t)=[Gi1(t),Gi2(t),…,Gin(t)]。在迭代過程中,粒子的個體最優位置為 種群最優位置為 更新公式為 式中:i?[1,m],i?[1,n],w為慣性權重[16],c1和c2為加速因子,r1和r2取區間[0,1]內的隨機數,t 為迭代數量。 粒子群算法具體流程步驟如下: 1)對數據集進行初始化,設置數據集中樣本的位置和速度,對種群評估初始最優位置gbest,給每個樣本設置個體最優位置pbest作為初始值。 2)對數據集中的樣本進行適應度函數計算得到適應度函數值。 3)評估數據集中的樣本,更新粒子個體的最優位置pbest。 4)評估種群的最優位置gbest。 5)更新樣本的速度和位置,將樣本位置移動至最優位置pbest 6)進行判定,如果失敗,則對所有樣本重新進行2)到5)的操作,如果成功,則輸出種群最優位置并結束循環。 為了考察上述的兩種算法在SVM 算法中的性能,通過設定一種算法來實現對SVM 算法的改進,對原始訓練樣本集使用基于密度的裁剪方法,然后通過對裁減之后的新訓練樣本集進行訓練建模并測試實驗。本文對于SVM 算法的粒子群參數尋優方法是將粒子群的位置變量設置為二維變量,即X1和X2,其中X1的取值范圍為(Cmin,Cmax),X1的取值范圍為(gmin,gmax),通過對X1和X2進行計算來對SVM 算法參數C 和g 進行尋優。改進算法具體步驟如下: 1)由于需要處理的數據,首先設定原始樣本集的數據為X=(xij)nxp,對原始訓練樣本集進行數據預處理,將數據各維歸一到[0,1]的范圍中,得到處理之后的數據集,便于剪裁算法進行計算。歸一化公式如式(18)。 2)通過上述裁剪算法對處理后的數據進行裁剪,裁減掉冗余樣本,生成新訓練樣本集。 3)對新訓練樣本集進行上述粒子群算法進行SVM 參數尋優,運行libsvm 工具箱中的svmtrain 函數,計算適應度值,建立優化后訓練模型。 4)通過svmpredict()函數對測試數據進行測試,得到準確率。 上述基于密度裁剪和粒子群算法的SVM 算法的具體算法流程如圖2所示。 圖2 具體算法流程圖 本文實驗是對UCI 標準數據庫中樣本集(Wdbc,Pima,Spambase,Shuttle)進行測試,驗證本文提出算法的有效性,而且UCI標準數據庫中的各類數據存在差異,在數據維度和數據分布情況上也皆不相同,所以可以比較客觀地驗證本文算法的可靠性。本文將在原始數據集中取訓練樣本集和測試樣本集比值為4∶1 進行測試分析,具體情況如表1所示。 表1 原始實驗數據集 采用上述提出的基于密度的裁剪方法進行裁減,得到裁剪率等于裁減掉的樣本數量與訓練樣本數量的比值,情況如表2所示。 表2 裁剪后實驗數據集 可以看到數據集的訓練樣本裁剪率在0.1~0.35 之間,在數據集維數較低時,裁剪的樣本數更高,但是在數據集維數較高時,裁剪的樣本數較低。然后對裁剪后的新訓練樣本使用libsvm 工具箱進行測試實驗,得到使用基于密度裁剪和粒子群算法前后的識別準確率結果如表3和圖3所示。 表3 使用算法前后準確率 圖3 使用算法前后準確率比較圖 對照使用基于密度裁剪和粒子群算法前后的數據,可以看出當使用算法后,所有測試數據的預測識別準確率均得到了提升,可以看到在Spambase數據集提升了11.5%的準確率,而在Wdbc 數據集中也有1%的準確率提升,可以說明使用基于裁剪和粒子群算法可以減少訓練樣本的部分冗余樣本,提高分類超平面劃分的準確程度,并提升SVM 算法的識別準確率。 本文介紹了SVM 算法,并對SVM 算法提出了改進方向,為了提升算法的準確率,分別使用了密度裁剪方法和粒子群尋優方法對SVM 算法進行研究和優化。對密度裁剪方法在實行過程中的算法進行了分析,分步驟的對實行過程算法進行了實現,討論了各個步驟算法實現的含義,通過對數據樣本的測試,較為有效地減少了訓練樣本的冗余樣本。對懲罰參數C 和核參數g 地粒子群算法進行了研究和使用,探討研究了實現原理和過程。通過使用UCI 數據庫的數據集對改進后算法進行實驗論證,通過結果表明確實有效地提升了SVM 算法的性能。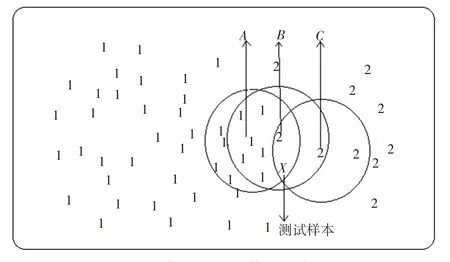
3.2 基于密度裁剪算法的參數確定
3.3 粒子群算法概述
3.4 基于密度裁剪和粒子群算法的SVM 算法實現

4 算法測試和實驗結果分析



5 結語

