Shape and diffusion instabilities of two non-spherical gas bubbles under ultrasonic conditions

Wurihan Bao(包烏日汗) and De-Xin Wang(王德鑫)

College of Physics and Electronics,Inner Mongolia Minzu University,Tongliao 028043,China

Keywords: non-spherical bubble,shape instability,diffusive instability

1.Introduction

When sound waves propagate through a liquid, they induce a sequence of cavitation phenomena within minute bubbles immersed in the liquid due to the influence of a driving acoustic field.[1]As the driving acoustic pressure attains the inertial cavitation threshold, the bubbles collapse, accompanied by concurrent light radiation under specific conditions,a phenomenon termed sonoluminescence.[2,3]In recent years,owing to the rapid progress in science and technology,the extensive application of ultrasonic cavitation technology has become prevalent across various domains, encompassing ultrasonic cleaning, pulverization, sterilization, ultrasonic extraction,and ultrasonic therapy.

The presence of multiple bubbles is primarily responsible for the acoustic cavitation effect in liquid.However,the intricate interplay between these bubbles and environmental conditions poses challenges for accurately simulating diverse experimental scenarios using numerical modeling.In contrast,simulating the cavitation of two bubbles in liquid is considerably more straightforward compared to the complexities associated with multiple-bubble acoustic cavitation.When subjected to a driving acoustic field, the oscillation of bubbles give rise to mutual attractive or repulsive forces, known as the secondary Bjerknes forces.Under the influence of the secondary Bjerknes forces, distinct acoustic phenomena occur on the bubbles immersed in the liquid,deviating from those observed in isolated bubble systems.[4–6]

Acoustic cavitation bubbles, renowned for their intricate dynamics, have instigated a comprehensive exploration spanning both theoretical and experimental domains.In this captivating realm, the attention has particularly focused on the dynamics of two gas bubbles due to their versatile applications.Noteworthy is the work of Luet al.,[7]who extended the theoretical framework by employing the velocity potential superposition theory to elucidate the complexities inherent in the ultrasonic dynamics of two gas bubbles with distinct frequencies.Their research not only sheds light on the intricate interactions intrinsic to bubble behavior but also establishes the groundwork for a deeper comprehension of their dynamics.Empirical insights further enrich this landscape.Maet al.[8–10]delved into the dynamics of bubble volume under secondary Bjerknes forces,utilizing the Lagrange equation to reveal the interplay of parameters influencing oscillation amplitude and initial phase.This empirical depth not only complements theoretical insights but also provides tangible validation through experimental observations.Extending the inquiry to non-spherical bubbles,Wanget al.[11]harnessed the modified Keller–Miksis equation to quantify fluctuations in the radius of two gas bubbles,secondary Bjerknes forces,and temperature during acoustic cavitation.These experimental findings seamlessly align with theoretical constructs,fortifying the foundational principles governing bubble dynamics.Moreover,the pioneering study conducted by Zilonovaet al.[12]has delved into the intriguing dynamics of bubble-bubble interactions within viscous media, revealing their pronounced influence on the behavior of individual bubbles.That study notably highlights a distance-dependent relationship, wherein mutual influence diminishes as the inter-bubble distance increases,becoming negligible at distances of a few millimeters.This insight assumes even greater significance when extended to the realm of viscous media,warranting further exploration.In the broader context of the cavitation of two bubbles, it is noteworthy to acknowledge the significant contributions of other researchers.Studies conducted in Refs.[13–19] have illuminated various facets of cavitation involving two bubbles,collectively enhancing our understanding of this intricate phenomenon.

In all of these investigations, Prosperettiet al.have predominantly focused on the stability characteristics of spherical bubbles, primarily considering the influence of fluid viscosity.However, the stability characteristics of non-spherical bubbles have not been addressed in their research.[20]Studies on bubble dynamics often rely on the assumption of ideal spherical bubbles.However, real-world experiments involve the presence of numerous non-spherical bubbles,rendering the spherical model inapplicable.Wanget al.[21]have proposed a non-spherical model for sonoluminescence in a non-spherical acoustic field and have determined a stable range for sonoluminescence.They have discovered that bubbles exhibit nonspherical oscillations within specific parameter intervals.Wuet al.have investigated the translation and non-spherical oscillation of a single bubble, concluding the work that, under a constant initial bubble radius and driving acoustic pressure amplitude, the non-spherical oscillation becomes more pronounced with an increasing initial speed of the bubble center.Moreover, the corresponding instability region in theR0–Paphase diagram gradually expands.[22]

In the present study,based upon literature,[16]we investigate the impact of various initial radius, distance, and perturbation parameters on the shape instability and diffusive equilibrium curve properties of two non-spherical gas bubbles.To accomplish this,we employ the modified Keller–Miksis equation.Our findings contribute theoretical evidence for the examination of instability characteristics in non-spherical multibubbles and bubble clouds.

2.Theoretical model for two non-spherical gas bubbles

To facilitate the analysis, we initially developed a simplified theoretical model of two non-spherical gas bubbles,as illustrated in Fig.1.Although this is a schematic diagram of a three-dimensional model,the bubble dynamics model under the three-dimensional model is very complex.In this study,only two non-spherical gas bubbles under two-dimensional conditions are considered, and their long radii of ellipses are represented asR1andR2respectively.It can be observed from Fig.1 thatr2=r1?d,whered=(0,0,d)represents the coordinate vector of the displacementdbetween bubbles.Assuming thatR1+R2?d, we consider a random pointPlocated outside the two bubbles,r1andr2represent the displacements of the centers of bubbles 1 and 2 from the pointP.Under the assumptions of an incompressible and irrotational ideal fluid,the particle velocity potential function at any point within the liquid satisfies the Laplace equation

If we take the central point of bubble 1 as the origin coordinate, the velocity potential of the liquid due solely to radial pulsations of bubble 1 is then represented as[16]

Similarly,potential generated by radial pulsations of bubble 2 would be

whereΦ1(r1)is the velocity potentials of bubble 1,Φ2(r2)is the velocity potentials of bubble 2, respectively.To carry out the calculation further we need to be able to transform coordinates from(r1,θ1)to(r2,θ2),and vice versa(see Fig.1).Herepnis thenthLegendre polynomial.We can expandΦ2in the local coordinate of bubble 1 as

Similarly,we haveΦ1in the local coordinate of bubble 2,

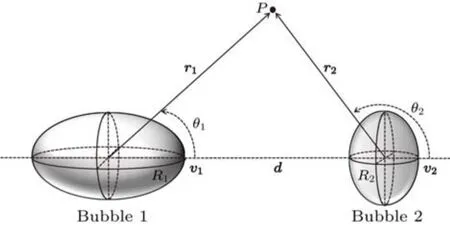
Fig.1.A three-dimensional schematic diagram of two non-spherical gas bubbles in an acoustic field.

To describe the oscillation of two non-spherical gas bubbles in the acoustic field, we introduce a perturbation in the driving acoustic pressure.The distance between the center point of any non-spherical bubble and any pointPon the surface of that bubble can be expressed as follows:[17]

whereRi(t) is the initial radius of the bubble with no perturbation.Ymn(θ,Φ) represents the spherical harmonics ofnorder, wheren ≥2, andai(t) is the amplitude of the surface distortion.During the oscillation process, the bubbles are rotationally symmetric.Then,we only need to consider the bubbles’radial oscillation,and their velocity potentials can be expressed as

We further view the part containingθiin Eq.(7)as a perturbation item and neglect its high order small quantities,then we obtain the velocity potentials inside and outside the nonspherical bubble interfaces as follows:

Then substituting Eq.(8) into the Bernoulli equation yields

whereP(ri)andP(∞)denote the pressures at the positionsPand infinity in the liquid,εis a small perturbation parameter,

whereμis the viscosity coefficient of the liquid, andσis the surface tension coefficient.P0is the ambient pressure,Pd=?Pasin(ωt)is the driving acoustic pressure on the bubble surface,ω=2π fwithfbeing the frequency of acoustic field,andγdenotes the polytropic exponent.

WhenPdis not too large, because of its symmetry, nonspherical bubbles from persisting for an extended period under uniform acoustic driving.Therefore, it becomes necessary to introduce a small non-spherical symmetrical acoustic pressure to correct the driving pressure:[23]

whereδis the boundary layer thickness,(i=1,2), onlyn=2 is considered in this study, quadruple distortion.By substituting the two-non-spherical-gas-bubble potentialΦ(ri,θi) into Eq.(9), whenr=R1, we can obtain the shape instability equation of bubble 1 as follows:

Similarly,whenr=R2,we can obtain the shape instability equation of bubble 2 as follows:

The right sides of Eqs.(14) and (16) describe the spherical asymmetric perturbation of sound waves,[23]whereδ pnrepresents the deviation of the driving sound pressure from the spherical symmetry.

Considering the compressibility of the liquid in a highly intense acoustic field,the Rayleigh–Plesset model cannot satisfy the requirement that the radial oscillation velocity of bubbles in the liquid is lower than the speed of sound.Consequently, in this study, we adopt the assumption of incompressible liquid.To meet this condition, we used the Keller–Miksis equation to describe the variation in the radius of two non-spherical gas bubbles, instead of the Rayleigh–Plesset equations (13) and (15).The Keller–Miksis equation is expressed as

3.Factors influencing the instability characteristics of two non-spherical gas bubbles

Compared to a single bubble, calculating the shape instabilityR0–Paphase diagram and diffusive equilibrium curve of two non-spherical gas bubbles requires more extensive effort and entails increased complexity.Therefore, our primary focus in this paper is to examine the influence of bubble radius, distance and perturbation parameter on the instability characteristics of cavitation bubbles.Based on previous research,[23,24]the instability of non-spherical bubbles can be classified into three main types: shape instability,diffusion instability, and chemical instability.The shape instability type can be further classified into three categories: (a) Rayleigh–Taylor(RT)instability,(b)rebound instability,and(c)parameter instability.Studies have confirmed that RT and parameter instabilities play a dominant role in the stability characteristics of bubbles, with their respectiveR0–Paphase diagrams exhibiting comparable features.Therefore, our investigation primarily focuses on the RT instability, for which the corresponding instability criterion can be expressed as[25]

To provide a more intuitive description of the instability characteristics of non-spherical bubbles,we conducted numerical simulations to observe the instability states over five acoustic cycles.We incorporated the parameter conditions for the three instabilities of a single bubble as provided in the literature[24]into our modified models for two non-spherical gas bubbles.Subsequently, we investigated the instability characteristics of the bubbles by considering the parameters of perturbation amplitude,which changes over time,and the bubble radii.These parameters are as follows: (a)R0=2.5 μm,Pa=1.5 atm;(b)R0=4.0μm,Pa=1.3 atm;(c)R0=5.2μm,Pa=1.0 atm.We performed calculations and generated diagrams illustrating the normalized perturbation amplitude as it varies with time and the bubbles’radii,presented in Figs.2(a)–2(c).Using Eqs.(13)–(16) and employing the Runge–Kutta method,we conducted numerical simulations for the three instabilities of non-spherical bubble.In our proposed model,we assigned the following physical parameters:f=25 kHz,ρ=1000 kg/m3,c=1485 m/s,γ=1.4,P0=1.013×105Pa,P0=P(∞),σ=0.0725 N/m,andμ=0.001 kg/m·s.

Figure 2(solid lines)illustrates the behavior of cavitation bubbles over five complete acoustic cycles.Within each cycle,the bubbles initially undergo slow expansion.During the first 0.5 cycles of acoustic pressure, their radii reach a peak and then sharply decrease.Subsequently, within 0.6 cycles of acoustic pressure, the radii reach their minima.Following this, the bubbles oscillate in a stable manner.The corresponding maximal expansion ratios of the cavitation bubbles for the three instabilities are 1.7, 8.0, and 20, respectively.It can be observed that the expansion ratios of the bubbles differ depending on their initial radius.Under the same amplitude of the driving pressure,it is observed that cavitation bubbles with larger initial radius tend to exhibit relatively higher expansion ratios.This phenomenon could potentially be attributed to the proximity of larger initial bubbles to the resonant radius within the examined parameters.Notably,previous studies[26–28]have demonstrated that the maximum expansion ratio is achieved when bubbles are driven under resonant conditions.The oscillation of the bubble radii can be roughly divided into three periods: expansion,collapse,and rebound.

In order to explore the impact of the initial radius, distance,and perturbation parameters of two bubbles on their instability characteristics, we conducted numerical simulations to obtain the shape instabilityR0–Paphase diagrams and diffusive equilibrium curves.The diffusive equilibrium condition can be mathematically expressed as[25]

Here,C∞is the gas concentration far away from the bubble,C0is the saturation(mass)concentration of the gas in liquid,and〈〉denotes the time average.

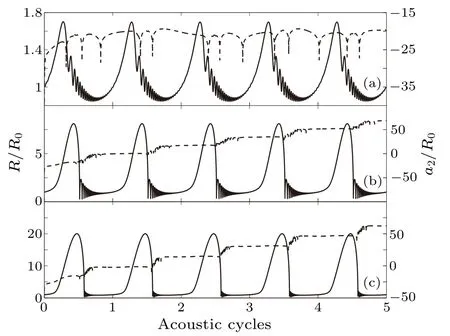
Fig.2.The dashed lines correspond to the normalized perturbation amplitude a2/R0 varying with acoustic cycles; the solid lines correspond to the radius R/R0 varying with acoustic cycles: (a) Rayleigh–Taylor instability(R0 =2.5μm, Pa =1.5 atm), (b)rebound instability(R0 =4.0 μm, Pa =1.3 atm), (c) parameter instability (R0 =5.2 μm,Pa=1.0 atm).

The shape instability caused by the interaction between two bubbles can be observed through the secondary Bjerknes force.[29]The secondary Bjerknes force between two gas bubbles can be expressed as

whereV1andV2denote the volumes of bubbles 1 and 2, respectively,V1=4/3πR31andV2=4/3πR32;eris the radial unit vector.In order to present the results,the variation of the secondary Bjerknes force is often portrayed using the secondary Bjerknes force coefficient,denoted asfB.It is defined as

Therefore,by observing the sign offB,we can discern the interaction between the two bubbles: whenfB＞0, the bubbles attract each other;whenfB＜0,the bubbles repel each other.

3.1.Influence of the radius between bubbles

Figures 3(b)–3(c)illustrate the influence of different initial radius of bubble 2 on the shape instability and the diffusion equilibrium curve of bubble 1 inR0–Paphase diagrams for the two-non-spherical-gas-bubble model presented in this paper.Figure 3(a) shows the results of a single bubble under the same conditions, in comparison with the two-bubble model.Bubbles are driven by sound waves with a frequency of 25 kHz in water at 293 K and 1 atm ambient pressure,without considering perturbation.In the figures,black areas represent regions of shape instability,whereas white areas represent regions of shape stability.The stability threshold corresponds to the boundary between the black and white areas of the figures.The curves represent the diffusive equilibrium of the bubble under different relative concentrations ofC∞/C0,with a positive slope indicating a stable diffusive equilibrium and a negative slope indicating an unstable diffusive equilibrium.

Fig.3.Shape instability and diffusive equilibrium curves in R0–Pa phase diagrams, under a constant distance d =20 mm without perturbation for various relative concentrations C∞/C0: (a)single bubble,[(b),(c)]the initial radius of bubble 2 with R20=1μm and R20=5μm,respectively.

It is known that in the case of single-bubble cavitation,after undergoing several oscillation cycles,due to rectification effects,the interior of the bubble eventually contains only argon gas.[30]The results presented in Figs.3(b) and 3(c) reveal important findings regarding the stability of two bubbles.When the distance between bubbles is kept constant, it becomes evident that the shape instability region of bubble 1 in theR0–Paphase diagram expands gradually as the initial radius of bubble 2 increases.Compared to the case of a single bubble,the unstable region has significantly increased,but its range is different.This could be due to the interaction forces between the two bubbles, specifically the secondary Bjerknes force, coming into play.In air and air-saturated water,the relative concentration of argon gas,C∞/C0=0.01.From Figs.3(b) and 3(c), it can be observed that with an increase in the initial radius of bubble 2, the curve ofC∞/C0=0.01 with a positive slope covers a decreasingParegion.This suggests that in terms of diffusive stability,due to the interaction forces between the two bubbles, the two-bubble model is not as stable as the single-bubble model under the same cavitation conditions.

Additionally, from Figs.3(b) and 3(c), it is evident that some continuous stable regions emerge within the instability region.The stability theory of Mathieu(or Hill)equation can provide a good understanding of the general characteristics of instability.[31]Bubble oscillations are highly nonlinear,the Mathieu (or Hill) equation replacesan=bn/R3/2and retains only the linear terms in the spherical asymmetric perturbation.Calculations using the Mathieu(or Hill)equation can explain the emergence of continuous stable regions within the instability region of theR0–Paphase diagram.[32]

3.2.Influence of the distance between bubbles

The distance between bubbles plays a significant role in the secondary Bjerknes forces.Unlike the behavior of a single bubble, where stability and dynamics are relatively wellunderstood,the presence of two bubbles introduces a new level of complexity.Due to the influence of secondary Bjerknes forces and variations in the inherent resonance frequencies of the two bubbles,varying initial distances between bubbles lead to distinct interactions.To investigate the influence of the distance between bubbles on the shape instability of bubble 1 in the presence of two non-spherical gas bubbles,we conducted simulations and generated the shape instabilityR0–Paphase diagrams and diffusive equilibrium curves without perturbation.When the initial radius of bubble 2 is 5 μm, the initial distances between bubbles shown in Figs.4(a) and 4(b) are 2 mm and 0.2 mm,respectively.

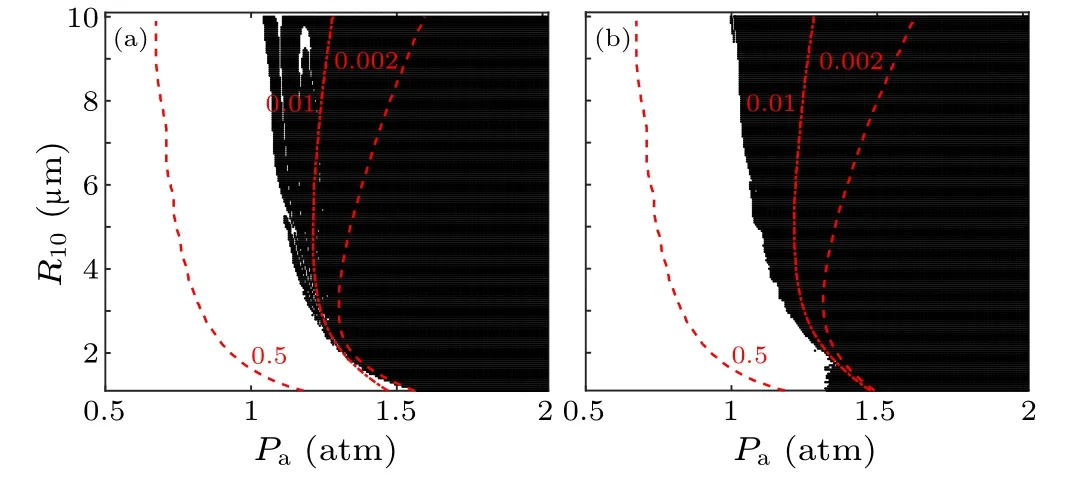
Fig.4.Shape instability and the diffusive equilibrium curves of bubble 1 in R0–Pa phase diagrams for various relative concentrations C∞/C0.The distance between bubbles is (a) d =2 mm and (b) d =0.2 mm,respectively.

Comparing Fig.3(c) with Fig.4, one can conclude that the unstable region gradually increases with the reducing distance between bubbles, which may due to the frequent fluctuations in secondary Bjerknes forces.Therefore, we calculated the variation of the secondary Bjerknes force coefficientfBin theR10–R20plane with different distance between bubbles,as shown in Fig.5.According to the region boundary in Fig.4,we selected the driving sound pressure as 1.15 atm.The white regions represent repulsive force,(i.e,fB＜0),while the gray scale regions represent attractive forces(i.e,fB＞0).The darker the color, the higher the absolute value offB.For better visualization, the complete symmetric data are shown.In Fig.5,as the distance between the bubbles reduces(i.e.,they approach each other),the repulsion region gradually decreases and the boundaries of these regions shift towards larger bubble radius,while the changes in the attraction region are minimal.This phenomenon may be attributed to the natural resonance of bubbles increasing as they approach each other.[29]Consequently, when bubbles approach each other, there is a possibility that the sign offBfor the cases near the boundaries changes, potentially leading to an inversion of the secondary Bjerknes force in some bubble pairs.A reduction in the distance between bubbles results in the widening of pressure ranges associated with the positive slope regions in the diffusion curves, particularly when considering a relative concentration ofC∞/C0at 0.01.This observation aligns harmoniously with the outcomes documented in earlier research studies.[25]

Fig.5.The variations of the secondary Bjerknes force coefficient fB in the R10–R20 plane for driving pressure Pa =1.15 atm under different distance between bubbles.The planes are given for distances: (a)d=20 mm,(b)d=2 mm,and(c)d=0.2 mm.

3.3.Influence of the spherical asymmetric perturbation parameter

The spherical asymmetric perturbation parameterδ p2in Eq.(12) is challenging to evaluate directly.In this paper,we have chosen to simplify by settingδ p2= 1×10?5Pa,1×10?7Pa,values that were previously used for a single bubble under similar conditions[23]and were demonstrated with the best fit to the experimental data in Ref.[33],and the parameters used in the instability analysis of other bubble models.[25]

In Figs.6(a)–6(c), we can see that, in the bubble-1 shape instabilityR0–Paphase diagram and diffusive equilibrium curve under a varying initial radius with driving pressure when the distance between bubbles is 20 mm,the initial radius of bubble 2 is 5μm and the spherical asymmetric perturbation parameterδ p2is 0Pa,1×10?5Pa,1×10?7Pa,respectively.

From Figs.6(a)and 6(b),we can observe that,under the same perturbation parameter,with the initial radius of bubble 2 in the two-bubble model being constant, the instability region of bubble 1 is larger compared to that of a single bubble.This illustrates that perturbation parameter has a substantial influence on the shape instability of bubbles.

Comparing Fig.3(c) with Fig.6, we can observe that in the presence of perturbation parameter in the two-bubble model, larger perturbation parameters lead to an increase in the instability region of bubble 1.

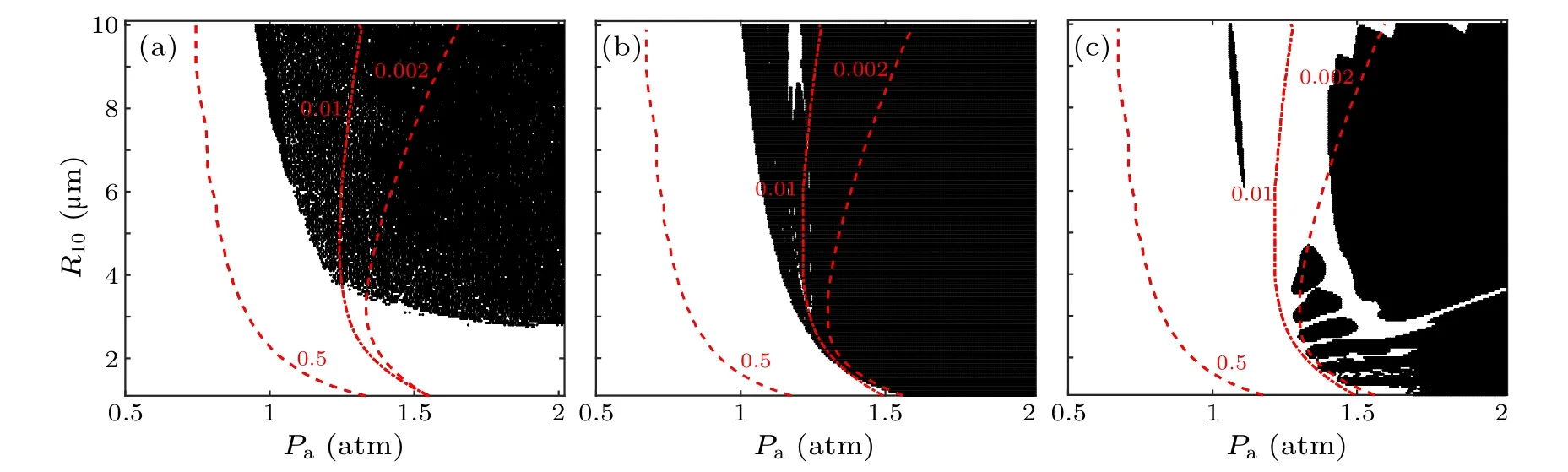
Fig.6.Shape instability and the diffusive equilibrium curves of bubble 1 in R0–Pa phase diagrams,for d=20 mm,and the spherical asymmetric perturbation parameter: (a) the single bubble model, δ p2 =1×10?5Pa, (b) the two-nonspherical-bubble model, R20 =5μm,δ p2=1×10?5Pa,(c)the two-nonspherical-bubble model,R20=5μm,δ p2=1×10?7Pa.

Conversely,smaller perturbation parameter tends to facilitate the formation of stable oscillations, resulting in a reduction of the instability region.However,it is important to note that the relationship between perturbation parameter and shape instability is likely nonlinear,and the specific mechanisms involved require further investigation.

From Figs.3(c), 6(b), and 6(c), we selected the region boundary as 1.3 atm and calculated the secondary Bjerknes force coefficientfBin theR10–R20plane corresponding to the three figures, as shown in Fig.7.The perturbation parameter has minimal impact on the overall trend of the secondary Bjerknes force.It only induces slight variations at the boundaries between the repulsion and attraction regions in the twononspherical-bubble model.

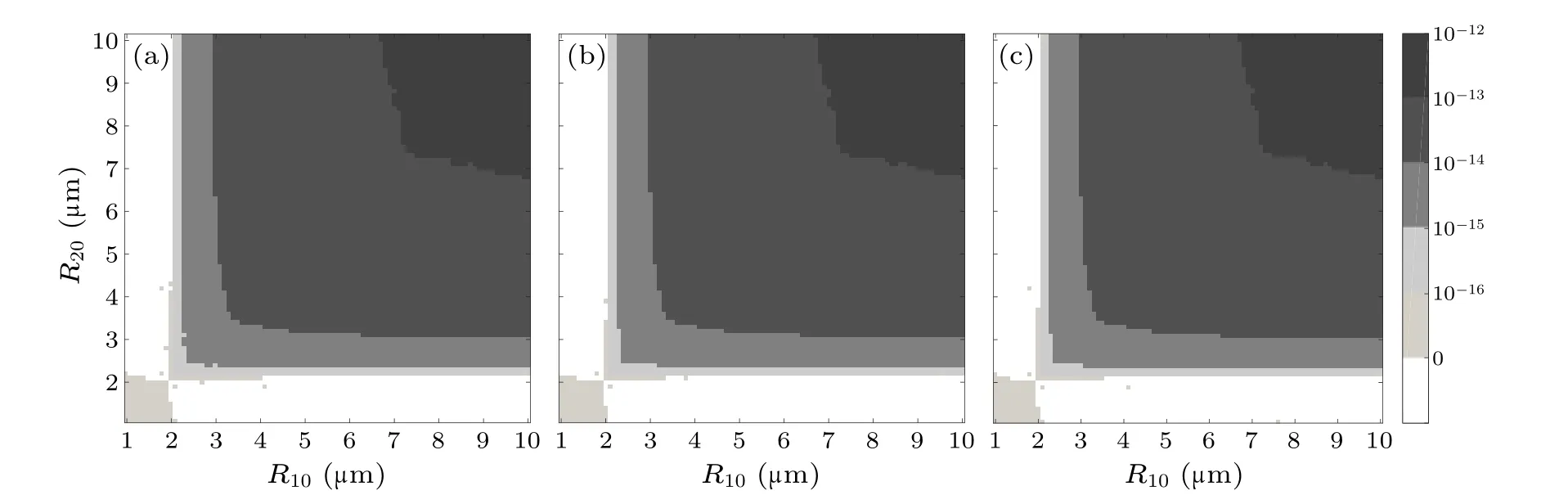
Fig.7.The secondary Bjerknes force coefficient fB in the R10–R20 plane for driving presure Pa=1.3 atm with different spherical asymmetric perturbation parameter.The planes are given for perturbation: (a)δ p2=0,(b)δ p2=1×10?5Pa,and(c)δ p2=1×10?7Pa.

4.Conclusion

We have investigated the instability characteristics of two-nonspherical-gas-bubble cavitation and explored the influence of various factors.Using numerical simulations and the Keller–Miksis equation, we establish a theoretical model considering initial bubble radius, distance, and perturbation parameter.With this model,we find the unique stability characteristics arising from interactions between two bubbles as opposed to a single bubble under similar cavitation conditions.The pivotal role played by the secondary Bjerknes force and resonance frequencies is highlighted.Furthermore,alterations in the initial distance of two bubbles and perturbation parameters exert substantial influence on the extent of the instability region.Notably,the nonlinear nature of the relationship between perturbation parameters and shape stability calls for further in-depth investigation to elucidate its intricacies.These findings contribute to understanding two-nonsphericalgas-bubble cavitation and provide a foundation for achieving stable bubble sonoluminescence.

Acknowledgment

Project supported by the Scientific Research Project of Higher Education in the Inner Mongolia Autonomous Region(Grant No.NJZY23100).