基于多模PPP-AR 技術的大氣水汽探測性能分析

郭秋英,薛學龍,余 淼,張海平,李國偉,畢京學

(1.山東建筑大學測繪地理信息學院,濟南 250101;2.山東省國土測繪院,濟南 250102)

0 引言

大氣中水汽含量雖然很少,卻是大氣中最活躍的成分之一[1]。大氣水汽的時空變化是災害性氣候形成的原因之一。因此,快速、精確地獲取大氣水汽對于氣象預報具有重要的意義[2]。

全球衛星導航系統(global navigation satellite system,GNSS)具有高時間分辨率、高精度和全天候的探測大氣水汽能力,彌補了傳統水汽探測技術的不足,成為探測水汽的重要技術手段。地基GNSS反演大氣可降水量(precipitable water vapor,PWV)主要有相對定位和精密單點定位(precise point positioning,PPP)兩種模式,都能得到精度較高的對流層延遲(zenith total delay,ZTD)[3]。相對定位需要引入遠距離測站進行聯合解算,才能有效消除大部分GNSS觀測誤差,從而提高GNSS反演PWV 的精度。而PPP不需引入遠距離測站進行解算,具有成本低、效率高及處理快等優勢[4]。此外,整周模糊度固定模式下的PPP(PPP ambiguity resolution,PPP-AR)技術的發展使得PPP 收斂時間進一步縮短[5],從而實現PWV 估值精度的提升。

目前,世界上有四個全球衛星導航系統,包括中國的北斗(BeiDou navigation satellite system,BDS)、美國的GPS、俄羅斯的GLONASS和歐盟的伽利略(Galileo),這些系統相互兼容、相互發展。利用多模GNSS組合可以增加觀測衛星數量,從而提高ZTD解算精度[6]。李星星等[7]使用單系統GNSS和多系統GNSS估計ZTD,實驗表明,與單一GNSS相比,多模GNSS實時ZTD估計可以實現毫米級的精度和高可靠性。LU[8]基于多GNSS(GLONASS+GPS+伽利略+北斗),利用當前GNSS的所有可用觀測結果,得到實時的ZTD/PWV 估值,可以實現毫米級的精度。李宏達等[9]利用GPS/BDS/GLONASS/Galileo組合獲取PWV 估值,實驗表明,多系統組合PPP估計ZTD的初始化時間縮短,且能夠獲取更高精度的ZTD和PWV。胡鵬[10]利用實時PPP 技術,分析了GNSS四系統反演水汽的精度差異,結果顯示,不同系統得到的ZTD/PWV 結果存在明顯的差異,多系統組合觀測獲取的水汽序列結果最為穩健,但沒有對北斗三號獲取的PWV 進行評估。夏鵬飛等[11]基于GNSS觀測數據與ERA-5資料,構建對流層模型;新的ZTD 模型優于后處理GNSS-ZTD 估值,研究結果表明,對浮點PPP求解施加ZTD 約束后,垂直方向的收斂時間也有顯著的改善。

以上研究結果表明,與單一或雙系統相比,多系統組合顯著提高了PWV 解算精度。由于北斗三號的B1C/B2a相較于其他頻點具有更好的信號強度[12],因此本文在利用北斗探測水汽時選擇B1C/B2a頻點。此外PPP-AR 在傳統PPP 的基礎上加入了模糊度固定的方法,可以提高定位精度和縮短收斂時間。因此本文基于最終精密星歷、采用不同方案下獲取ZTD 并進一步轉換為PWV,從PPPZTD 與IGS-ZTD 的相關性、PPP-ZTD 的收斂時間、PPP-ZTD 的精度以及PPP-PWV 的精度4個方面評價PPP-AR 探測大氣水汽的性能,對于GNSS氣象學應用具有重要的意義。

1 PPP反演大氣水汽的原理與方法

1.1 PPP基本觀測模型

GNSS PPP中偽距和載波相位觀測方程可表示為

式中,Pj,Lj分別表示偽距和載波相位觀測量;上標s為觀測的衛星號;G,C,R,E 分別表示GPS,BDS,GLONASS和Galileo;下標j為載波的頻率;ρs為衛星s至接收機的幾何距離;c為真空中光速;dtr,dts分別為接收機和衛星鐘差;d0為衛星軌道誤差;tSTD為對流層斜路徑延遲;為電離層延遲;分別為接收機端和衛星端的偽距硬件延遲;分別為接收機端和衛星端載波相位硬件延遲;為偽距觀測值殘差;為載波相位觀測噪聲和其他誤差。

BDS-3中B1I/B3I偽距偏差可以通過無電離層組合消除,而BDS-3中B1C/B2a無法消除,為了進行改正,可以使用差分碼偏差(differential code bias,DCB)產品進行改正,公式為[13]

在PPP解算中,由于未檢校的相位延遲(uncalibrated phase delay,UPD)被模糊度吸收,導致模糊度不具備整數特性,無法直接固定為整數。因此,精確地將相位偏差進行分離并改正是實現PPP模糊度固定的關鍵,目前通常采用整數鐘差法或UPD 法來消除相位偏差帶來的影響。

1.2 模糊度固定方法

1.2.1 寬巷模糊度固定

模糊度固定一般采用寬窄巷(wide lane-narrow lane,WL-NL)的一個固定的過程[14],melbournewubbena(MW)組合觀測值可以轉換為

為了避免偽距噪聲的影響,在計算LsMW時需要對偽距載波觀測值進行平滑處理。具體如下

對平滑后的寬巷模糊度進行星間單差計算,首先,根據寬巷模糊度固定殘差和高度角的關系,選擇高度角最大的衛星作為基準星,通過計算得到星間單差寬巷模度。然后,對星間單差模糊度取整,在進行取整前后,寬巷模糊度的絕對值差值不大于0.25,則進一步進行下列驗證

其中

式中,P表示模糊度固定成功率;為星間單差模糊度的實數解;為單差模糊度整數解;σ為求得的模糊度中誤差。

1.2.2 窄巷模糊度固定

經過寬巷模糊度固定后,開始進行窄巷模糊度固定。根據估計的模糊度實數解和星間單差寬巷模糊度可以得出星間窄巷模糊度實數解,公式如下

其對應的協方差陣為

在LAMBDA 算法中,精密單點定位的窄巷模糊度搜索時,其輸入量分別為浮點解參數個數、固定解參數個數、具有整數特性的實數解、對應的協方差矩陣以及固定解和固定解的殘差平方和。整數最小二乘被認為是模糊度取整方法中最嚴謹的方法,獲取的解為最優解。一般將最優解和次優解進行Ratio檢驗

1.3 PPP水汽反演的原理

斜路徑對流層延遲(slant total delay,STD)可以由映射函數、水平梯度、干延遲(zenith hydrostatic delay,ZHD)與濕延遲(zenith wet delay,ZWD)構成

式中,Md為ZHD 映射函數;MW為ZWD 映射函數;ΔLg(e,a)為大氣在水平方向梯度變化引起的誤差;e為衛星的截止高度角;a為衛星的方位角。

一般采用Saastamoinen模型來計算ZHD

式中,p為測站下氣壓,單位為hPa;H為測站高度,單位為m;φ為以弧度為單位的緯度。

GNSS衛星信號STD 映射到觀測站的天頂方向上得到ZTD,ZTD 減去ZHD 可以得到ZWD,然后利用ZWD 與PWV 的轉換關系獲得PWV。1994年,Bevis等[15]給出了ZWD 到PWV 的轉換公式,計算方法為

式中,Π為水汽轉換系數;ρ為液態水密度;k1=77.604 K/hPa,k2=64.790 K/hPa,k3=3.776×105K2/h Pa分別為大氣折射率試驗常數;k'2=k2-16.52;Rv=0.462 J·g-1·K-1為水汽氣體常數;Rd=0.287 J·g-1·K-1為干空氣氣體常數;Tm為大氣加權平均溫度。其中Tm采用Bevis經驗公式。基于上述方法就可以獲取測站上方的PWV。

2 基于PPP-AR獲取ZTD,PWV的性能分析

2.1 數據獲取與實驗方案

為評估多模PPP-AR在反演水汽方面的能力,選取全球范圍16個MGEX 觀測站,2022年3月11日到3月17日(年積日70—76)、5月7日到5月13日(年積日126—132)、7月8日到7月14日(年積日189—195)、10月23日到10月29日(年積日294—300)4個時間段的觀測數據。采用GPS(G)、BDS-3(C)、GPS+BDS-3(GC)、GPS+GLO+GAL+BDS-3(GREC)以及多系統浮點解(float-GREC)五種方案對ZTD與PWV進行估值,其中GPS采用L1/L2、BDS-3 采用B1C/B2a、GLONASS 采用L1/L2、Galileo采用E1/E5a雙頻頻點,前四種方案為PPP-AR,最后方案為多系統浮點解。實驗選取全球范圍16個MGEX 觀測站分布圖見圖1。

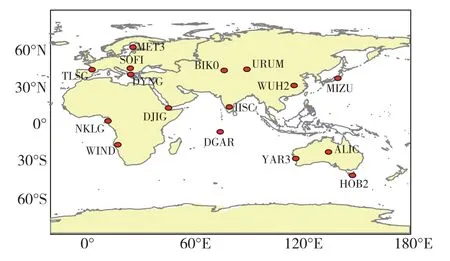
圖1 全球范圍16個MGEX觀測站分布圖Fig.1 Distribution map of 16 MGEX observation stations around the world

實驗采用武漢大學IGS數據中心提供的最終精密星歷產品。該產品具有較高的精度和時效性,可用于水汽的探測。本文使用Net_Diff 1.16軟件進行解算,該軟件能夠支持所有GNSS系統和所有頻率信號、GNSS觀測數據和產品下載、雙頻和三頻PPP與PPP-AR 的解算等;且在數據處理過程中,該軟件可以更加直觀地選擇不同的頻點及其組合。具體解算策略如表1所示。

表1 數據解算策略Tab.1 Data solution strategy

自1998年以來,國際GNSS服務(international GNSS service,IGS)采用地面觀測站數據并結合最終精密衛星軌道、衛星截止高度角為7°,基于PPP技術獲取每日時間分辨率為5 min的ZTD 產品,精度約為4 mm[17]。這些對流層產品以每日文件的形式提供,覆蓋了IGS網絡中的350多個全球導航衛星系統(GNSS)站點。因此,一般將IGS-ZTD 作為參考值。

2.2 多模GNSS探測水汽的性能分析

為分析多模PPP-AR 在探測水汽方面的性能,對不同時間段和不同衛星組合獲取ZTD 與PWV的估值進行了比較。從PPP-ZTD 與IGS-ZTD 的相關性、PPP-ZTD 收斂時間、PPP-ZTD 估值精度及PPP-PWV 估值精度4個方面評價多模PPP-AR 探測水汽的性能。

2.2.1 GNSS PPP-ZTD與IGS-ZTD的相關性分析

以IGS 發布的對流層產品(IGS-ZTD)作為參考值,評估不同方案下得到ZTD 估值與IGS-ZTD的相關性。圖2展示了2022年3月11日到3月17日(年積日70—76)ALIC 測站5 種方案下獲取ZTD 估值與IGS-ZTD 值的相關性。

圖2 ALIC測站不同星座組合的相關性Fig.2 Correlation of different constellation combinations of ALIC stations

由圖2可以看出,單系統獲取ZTD與IGS-ZTD的相關系數(0.902)與單系統C雙頻B1C/B2a的相關系數(0.895),兩者相關系數相當。雙系統GC相關系數(0.936)高于單系統G 和單系統C雙頻B1C/B2a的相關系數。這表明使用兩個衛星系統進行組合可以提高相關性。此外,多系統的相關系數(0.938)比雙系統的相關系數更高,意味著使用更多衛星系統進行組合時,相關性會進一步增強。相較于float-GREC組合,GREC也展示了更好的相關性。

2.2.2 GNSS PPP-ZTD 收斂時間分析

以IGS 發布的對流層產品(IGS-ZTD)作為參考值,評估ZTD 序列的收斂時間。當GNSS PPPZTD 與IGS-ZTD 差值小于20 mm,并且連續20個歷元差值保持在20 mm 內,認為收斂完成,這個過程需要的時間稱為收斂時間。圖3為DGAR 測站4個不同時間段、5種方案下的收斂時間。

圖3 DGAR 測站不同時間段、不同組合下的收斂時間Fig.3 Convergence time of DGAR station under different time periods and combinations

圖3顯示了DGAR 測站4個不同時間段的收斂過程。在PPP收斂的過程中,剛開始各方案的初始ZTD 與IGS-ZTD 之間存在較大的差值,隨著時間的推移,GNSS PPP-ZTD 與IGS-ZTD 之間的差值逐漸減小,并且變化趨勢逐漸趨于一致。可以看出,雙系統的收斂時間小于單系統的收斂時間,而多系統的收斂時間更加迅速,固定解在浮點解的基礎之上實現了更加迅速的收斂。多系統PPP 具有更好的收斂性能,可顯著提高ZTD 估計的準確性和穩定性。通過融合多個系統的信息,組合PPP可以更快地獲取ZTD 的估值。為了更加直觀體現測站的收斂時間,統計了所有測站不同時間段下的收斂時間,如圖4所示。

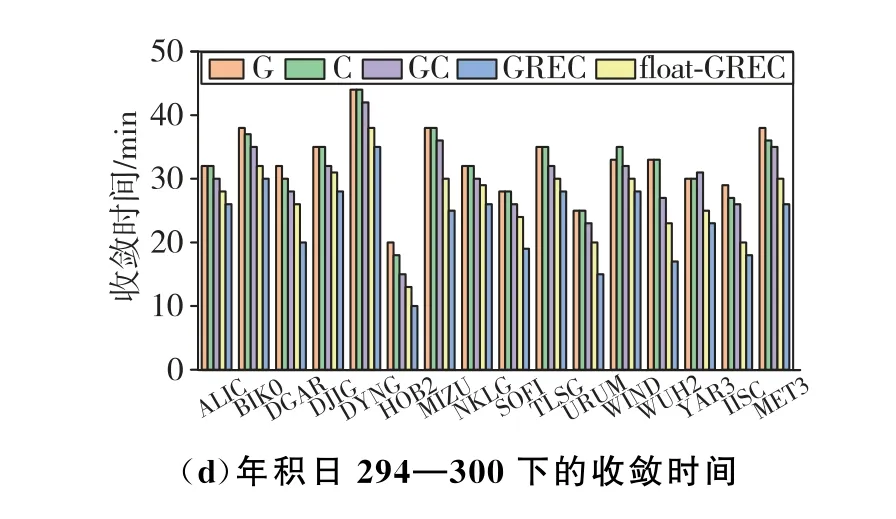
圖4 不同時間段各測站平均收斂時間Fig.4 Average convergence time of each station in different time periods

由圖4可以看出,在4個不同時間段的測站中,基于最終精密星歷獲取的單系統G 和C雙頻B1C/B2a的平均收斂時間分別為32,33,34,33和31,32,34,32 min,雙系統GC 的平均收斂時間分別為29,30,31和30 min,多系統固定解GREC 平均收斂時間分別為23,23,26 和24 min,多系統浮點解GREC平均收斂時間分別為26,27,28,27 min。根據研究數據表明:與G,C,GC 相比,多系統固定解GREC的收斂時間分別縮短了27%,25%和20%。此外,多系統固定解相比于多系統浮點解的收斂時間縮短11%。

這些收斂時間表明多系統固定解GREC 在不同時間段的收斂速度較快,相較于單系統和雙系統組合,具有更高的效率和性能。由于多系統在單、雙系統的基礎之上獲得了更多的衛星數量,觀測幾何圖形也得到了改進。這有助于PPP的收斂,進而改善ZTD 的收斂時間和PWV 估值精度。而多系統浮點解也表現出一定的優勢,雖不如多系統固定解GREC的收斂速度快,但相較于單系統G 和C固定解仍有改進。因此,多系統PPP-AR 技術在大氣水汽探測中表現出顯著的優勢。

2.2.3 GNSS PPP反演的ZTD 精度分析

為分析不同時間段、不同星座組合下的ZTD 估值精度,選取了ALIC,BIK0兩個測站,分別計算了不同方案下獲取的ZTD 估值與對應參考值IGSZTD 之間的偏差。以平均偏差和均方根誤差作為精度評價指標,ALIC,BIK0測站不同時間段、不同星座組合ZTD 精度對比見表2。

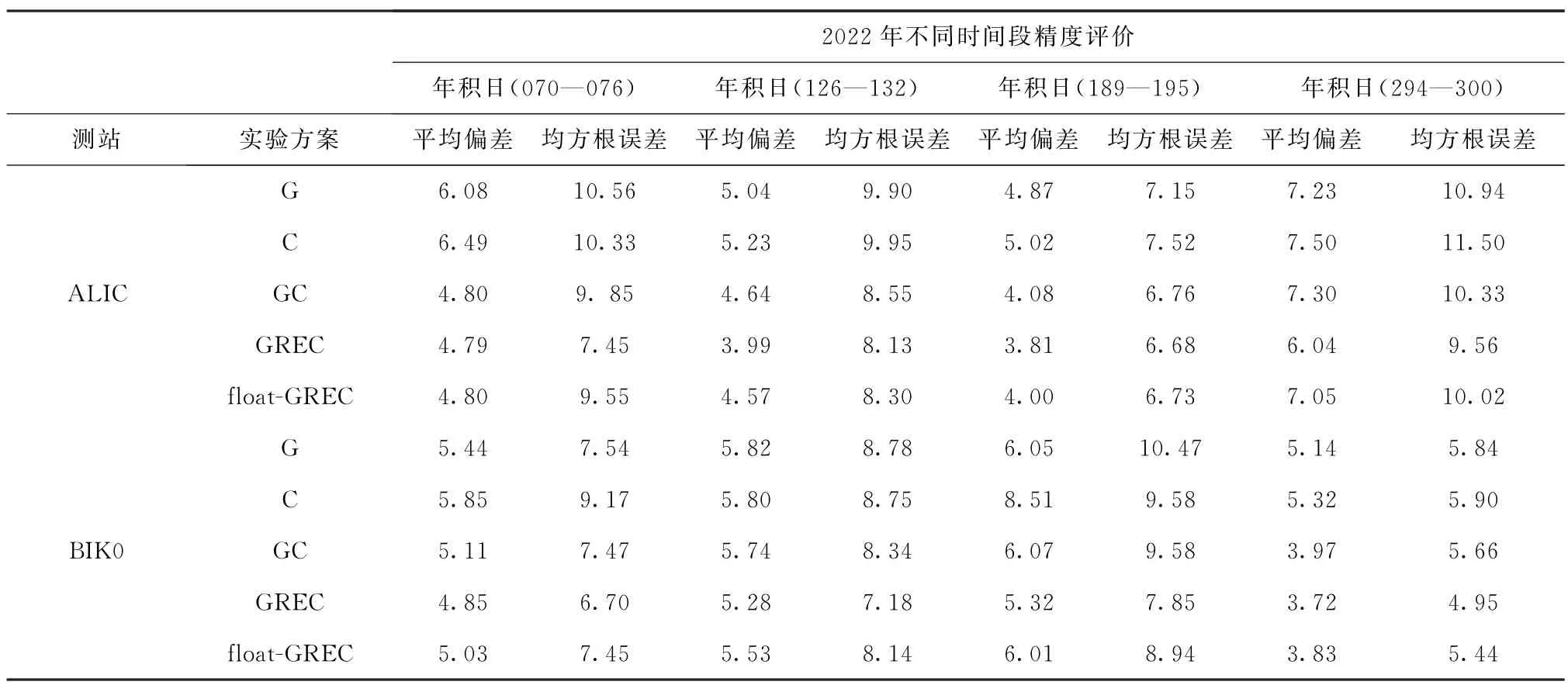
表2 ALIC、BIK0測站不同時間段、不同星座組合ZTD精度對比Tab.2 Comparison of ZTD accuracy of ALIC and BIK0 stations in different time periods and constellation combinations mm

表2 統計了ALIC 與BIK0 測站在不同時間段、不同星座組合下的ZTD 精度,GREC 組合獲得的ZTD 估值性能比單、雙系統有所提高,能夠獲得更高精度的ZTD 估值。可見,與單系統和雙系統解算相比,多系統PPP解算ZTD 估值精度更高。

2.2.4 GNSS PPP反演PWV 的性能分析

以探空站PWV(radiosondes precipitable water vapor,RS-PWV)為參考值,對上述5種方案反演的PWV 精度進行分析。由于探空站每天只有兩個時段(UTC時間00.00和12.00)的數據,因此在分析時只保留與探空站時段一致的PWV。另外,HOB2站與探空站(編號94975)相距25.1 km,WUH2與探空站(編號57494)相距5.2 km,且對流層延遲具有較強的時空差異性,故分析時只采用這兩個站的PWV。5種方案獲得HOB2 測站的PWV 與探空站94975獲取的PWV 對比見圖5(a);5種方案獲得WUH2 測站的PWV 與探空站57494 獲取的PWV 對比見圖5(b)。

圖5 HOB2和WUH2站與探空站(編號94975,57494)對比Fig.5 Comparison of HOB2 and WUH2 stations with sounding stations(No.94975,57494)

由圖5可知,G,C,GC,GREC,float-GREC這5種方案得到PWV 與RS-PWV 之間的差值大部分在10 mm 之內,GREC組合獲取的PWV 整體的變化更趨向于RS-PWV。以探空站RS-PWV 為參考值,5種方案計算的WUH2和HOB2站的PWV 與其相應的探空站PWV 的均方根誤差見表3。

表3 WUH2與HOB2站PWV的精度對比Tab.3 Comparison of PWV accuracy between WUH2 and HOB2 stations

由表3可知,相較于單系統(G)固定解、單系統(C)固定解、雙系統固定解及多系統浮點解,多系統固定解獲取PWV 估值展示了更好的性能。WUH2和HOB2測站雙系統GC解算均方根誤差較單系統G,C雙頻B1C/B2a減少0.21 mm,0.29 mm 和0.10 mm,0.05 mm;相較于GC 組合,GREC 組合的PWV 精度進一步提升,WUH2 和HOB2 測站均方根誤差減少0.02 mm 和0.10 mm;相較于float-GREC 組合,GREC組合精度也有所提升,WUH2 測站均方根誤差減少0.02 mm,HOB2測站均方根誤差減少0.08 mm。

3 結論

本文通過研究多模PPP-AR 技術反演大氣水汽的性能,得到如下結論。

1)在相關性方面:多系統組合ZTD 估值與IGS-ZTD 值相關性最高,時間序列更加穩健、平滑。此外,GREC組合估計ZTD 值更加連續、可靠。

2)在收斂時間方面:在不同的時間段基于最終精密星歷獲取ZTD,多系統展示了更快的收斂速度,相較于單、雙系統收斂時間分別縮短了27%,25%和20%。多系統固定解相較于多系統浮點解,收斂時間縮短了11%,表現出良好的性能。

3)在ZTD 精度方面:以平均偏差和均方根誤差作為精度評價指標,發現多系統狀態下精度最高,由于GREC組合可觀測到更多的衛星和更好的空間結構,由此可改善ZTD 的精度。

4)在PWV 精度方面:基于北斗三號雙頻B1C/B2a反演的PWV 與GPS的精度相當,基于多系統組合PPP-AR 反演的PWV 與探空站PWV 最為接近,效果最好。

以上結果表明,在水汽探測方面,北斗三號雙頻B1C/B2a獲取PWV 估值與GPS效果相當,在多系統的狀態下性能更佳,可以獲得更高精度的PWV 估值,為高精度的天氣預報提供有利的參考數據。