冷卻三角進出口阻力計算分析與研究

高志廣，王 鋒，李 誠，范 攀

（中國電力工程顧問集團西北電力設計院有限公司，陜西 西安 710075）

0 引言

空冷散熱器作為空冷系統的核心元件，其性能對冷卻系統運行和設計影響較大。系統規劃和設計時，為了提高空間利用效率，通常將空冷散熱器以冷卻三角的形式進行布置，如圖1所示。為節省支撐結構和投資，散熱器通常豎直布置。從頂視圖或橫截面來看，由若干組冷卻管束組合而成的兩個冷卻柱構成一個等腰三角形，調節進風的百葉窗布置在等腰三角形頂角的對邊位置。冷空氣經由百葉窗后進入三角內部，在掠過兩個冷卻柱時，通過翅片及換熱管外壁與換熱管內的熱水發生間接換熱，將熱水中的熱量傳遞到環境空氣中。

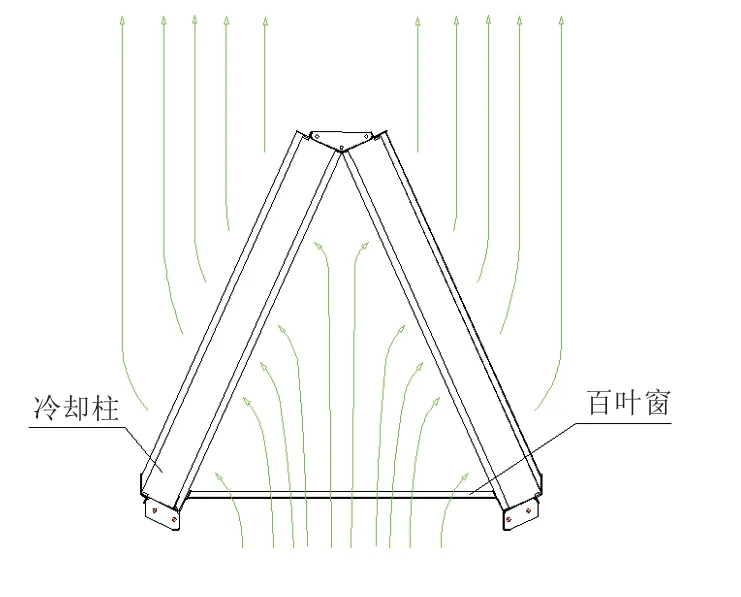
圖1 冷卻三角頂視圖

空冷換熱器的傳熱及阻力性能試驗通常以元件試驗(單個管束或冷卻柱)的形式開展，試驗條件與實際工程中冷卻三角的工作條件存在一定的差異。系統設計計算時，往往需要對試驗得到的性能參數進行必要的修正，以更加準確的計算和預測工程條件下空冷散熱器熱力和阻力性能。

冷卻三角頂角決定了氣流流經散熱器的偏轉程度，其大小直接影響到空冷換熱器進口和出口空氣流動狀態和附加阻力，對散熱器性能影響較大。

冷卻三角夾角的選擇，通常需要綜合占地、通風阻力、換熱效果等多種因素綜合確定。這就需要了解和掌握冷卻三角頂角對進出口阻力的影響。

1 冷卻三角進出口阻力計算

有關冷卻三角進出口阻力的計算方法較多，本文選取國內工程設計中較典型的兩種計算方法進行介紹和計算，并與數值模擬試驗結果進行對比和分析。

1.1 設計規范公式

DL/T 5545—2018《火力發電廠間接空冷系統設計規范》[1]對于冷卻三角進口及出口阻力計算推薦的計算公式如下：

散熱器進口阻力可按下列計算：

式中：ΔPhi為散熱器進口的阻力，Pa；Khi為冷卻三角進口阻力系數；vh為通過散熱器迎風面空氣流速，m/s；α為冷卻三角頂角，°，40°≤α≤70°。

散熱器出口阻力可按下列計算：

式中：ΔPho為散熱器出口阻力，Pa；Kho為冷卻三角出口阻力系數。

1.2 設計手冊公式

《電力工程設計手冊-火力發電廠水工設計》[2]中對于冷卻三角進出口阻力計算公式與設計規范公式一致，但阻力系數的計算公式不太一樣。

電力工程設計手冊中推薦的冷卻三角進口阻力系數計算公式如下：

式中：θ為冷卻三角頂角的半角，°；θ=α/2；θm為考慮流線偏離的修正半角，°。

冷卻三角出口阻力系數可按下式計算：

2 數值模型的建立與求解

為探究冷卻三角夾角對其進出口阻力的影響，特別設計了以下數值模擬試驗。通過在模擬風洞中放置不同頂角的冷卻三角，得到不同風速條件下三角前后及內部速度場和壓力場分布。

2.1 數值模型

本文數值模擬試驗包含風洞及一對散熱器(2片)，散熱器夾角由45°增加至180°。與通常環境風影響研究不同，本研究中將兩片散熱器設為多孔介質，具有一定的厚度，散熱器內流體僅允許沿翅片方向單向流動。流體正交方向通過散熱器的阻力根據迎面風速按照散熱器性能測試結果給定。

空氣流場的通用控制方程包括連續性方程、動量方程、能量方程、氣體狀態方程、k-ε方程、組分輸運方程等。

采用商業CFD計算軟件及有限容積法對上述三維數學模型進行求解計算，原理是將一個連續求解域分割成有限個單元，用未知參數方程表征單元特性，然后將各個單元的特征方程組合成大型代數方程組，通過求解方程組得到節點上的未知參數，從而獲得需要考察的參數數據。

離散方程的求解采用分離變量法，速度與壓力的解耦采用SIMPLEC算法。速度和溫度場的離散格式采用QUICK格式。動量和能量方程采用二階迎風格式進行離散，在迭代計算過程中能量方程和其他的守恒方程求解變量殘差值分別要求小于10-6和10-4。

2.2 計算結果

如圖2所示為計算得到的不同夾角條件下散熱器前后速度場分布情況。空氣流至冷卻三角入口后，受到散熱器冷卻柱的阻擋，沿流動方向流道逐漸變窄，流速明顯增加。

圖2 不同夾角冷卻三角附近速度場分布

翅片導流作用下，氣流在散熱器迎風面發生偏轉，在散熱器內部，空氣流動方向與散熱器厚度方向平行。翅片通道內，速度由高變低，存在一個減速過程。受冷卻柱阻擋的影響，流經散熱器迎風面的空氣分布并非均勻分布，在冷卻三角兩底角區域，流速相對偏低。

當空氣從散熱器流出后，流向再次發生偏轉。冷卻三角頂角的下游區域為低速流動區，該區域范圍隨著散熱器夾角的增大而減小。

如圖3所示為計算得到的不同夾角條件下散熱器前后的壓力場分布情況。

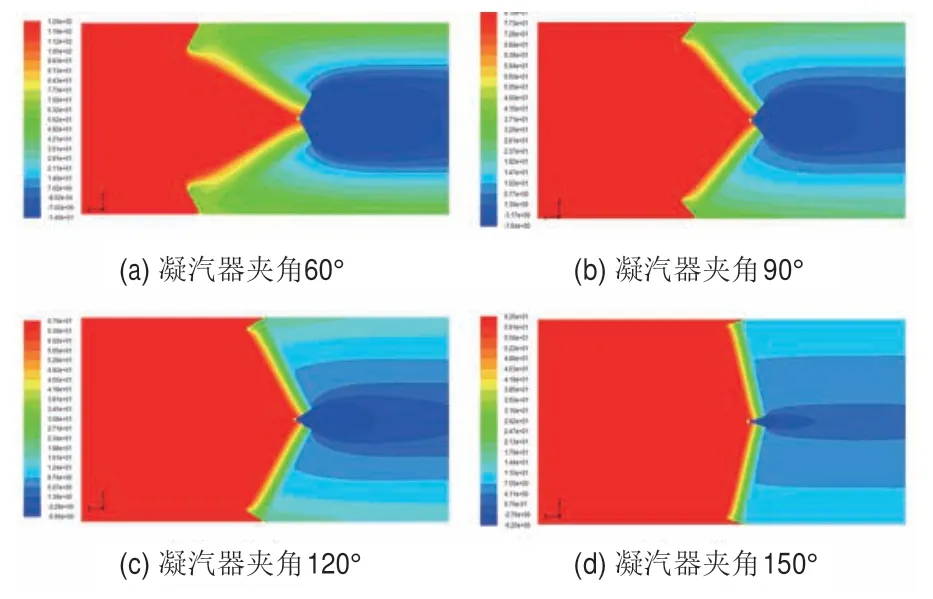
圖3 不同夾角冷卻三角附近壓力場分布

從散熱器迎風面開始，在翅片通道的前段，壓力分布存在一個由高到低的突變。結合前面的流場分析，這可能是由于散熱器迎風面處流體流動方向改變引起近翅片處流體產生偏離及彌合，在這個區域發生紊流產生較大的壓降所致。

空氣從散熱器流出后，在垂直于流動方向的平面上產生較為明顯的壓力梯度，靠近底角的區域總壓相對較高，靠近頂角的區域總壓相對較低，存在一個由等腰三角形兩側向中心逐漸貶低的總壓差。這個總壓差導致空氣流過散熱器后產生一定的紊動，在冷卻三角頂角下游附近甚至會出現漩渦。

過散熱器后流場紊動將會逐漸減弱，直到經過一定距離后，重新恢復為均勻流場。

2.3 進出口阻力系數的求取

在上述風洞內散熱器前進風口區域和散熱器后出風口區域分別選取流場相對均勻的兩個斷面，統計兩斷面平均總壓的差值，即為散熱器三角的阻力P散熱器三角。

該阻力由兩部分組成，一部分是單片散熱器的阻力，既散熱器迎風面和背風面的總壓差P散熱器。其阻力系數近似于單片散熱器在性能試驗時所測得的阻力系數。另一部分便是由于冷卻三角布置形式造成的散熱器進風口和出風口空氣流向改變及相互干擾而引起的附加阻力P進出口。

散熱器三角進出口的阻力P進出口為可通過散熱器三角阻力P散熱器三角與散熱器的阻力P散熱器之差獲得。見表1所列，以夾角為90°的冷卻三角數模結果統計和整理為例，說明冷卻三角進出口阻力系數的求取過程。

表1 冷卻三角(夾角90°)阻力系數整理計算表

從計算結果來看，冷卻三角頂角夾角為90°時，冷卻三角進出口阻力系數基本不隨迎面風速的變化而改變，其值約為3.0左右。冷卻三角進出口阻力在整個散熱器三角阻力中占比在10%～13%的范圍。

3 數值模擬結果與分析

3.1 進出口阻力計算結果

對于頂角夾角為60°、75°、120°、150°、180°時的冷卻三角阻力進行如表1所列的數據處理，可得到不同頂角夾角時冷卻三角進出口阻力變化規律如圖4所示。

圖4 不同夾角冷卻三角進出口阻力統計結果

隨著迎面風速的增大和夾角的減小，冷卻三角進出口阻力值呈現出逐漸增高的趨勢。以自然通風間接空冷系統常見的1.62 m/s左右風速為例，當冷卻三角頂角角度由60°增加至180°，冷卻三角進出口阻力值從13.3 Pa逐步降低至約1.3 Pa。

3.2 進出口阻力系數計算公式

利用計算得到的進出口阻力和迎風面風速，代入阻力計算公式可以得到冷卻三角進出口阻力系數。

阻力系數ξ的計算公式如下：

如圖5所示，散熱器ξ進出口阻力系數隨其夾角α增加而減小，其函數可擬合為如下冪函數：

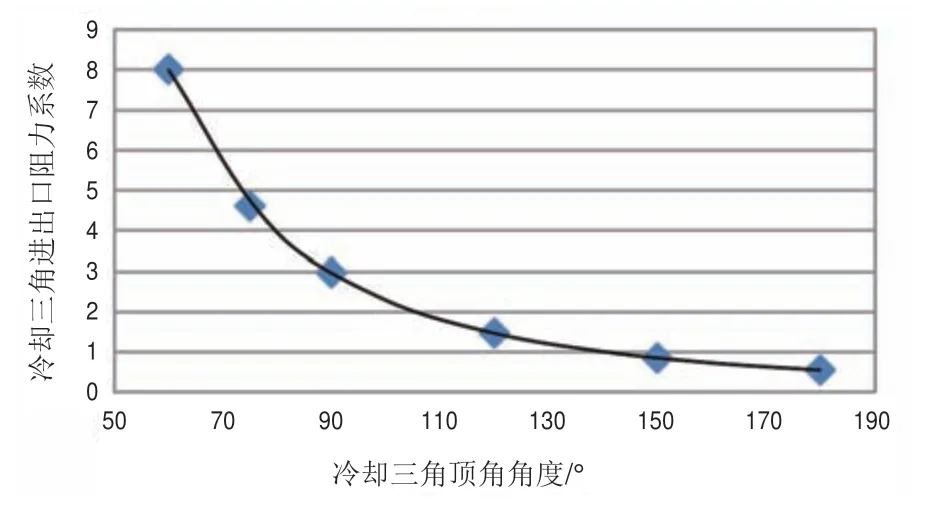
圖5 冷卻三角進出口阻力系數計算結果

3.3 與現有計算公式結果對比

將采用設計規范式(2)和式(4)和采用設計手冊式(5)和式(7)計算得到的冷卻三角進出口阻力系數與數值模擬試驗結果數據進行對比，見表2所列。

表2 公式計算阻力系數與數模計算阻力系數對比

在頂角40～70°范圍內，設計規范公式、設計手冊公式以及數值模擬計算得到的冷卻三角進出口阻力系數具有相同的變化趨勢。

超出70°范圍，設計規范公式計算得到的進出口阻力系數與數值模擬結果偏差就比較大。這與設計規范公式是基于大量試驗數據擬合有關。因此，在使用式(2)和式(4)時應特別注意校驗冷卻三角頂角角度是否在40～70°的適用范圍內。

設計手冊計算公式適用范圍更寬泛一些。在本文數值模擬研究的角度范圍內，公式計算結果與數值模擬結果變化規律吻合的較好。數值模擬試驗獲得的進出口阻力系數稍高于式(5)和式(7)的計算值。受限于計算速度和能力，數值模擬試驗采用的散熱器尺寸約為2 m×2 m×0.4 m，較小的長寬比意味著相對較大的阻風投影面積，可能會導致較高的阻力系數。

3.4 半理論計算公式的驗證

設計手冊計算公式之所以適用范圍更大，是因為采用了Kr?ger等提出的半理論半經驗公式。

散熱器進口阻力系數計算式(5)的提出和推導基于以下理論：如圖6所示，散熱器外來空氣流在經過散熱器翅片時，流動方向發生改變，在剛進入翅片處背風面一側出現流體分離，發生流體分離處的空氣流速v1較高。翅片通道內，流體經過充分混合后，流速逐漸趨于均勻。流體流出翅片時的空氣流速記為v3，v1大于v3，且滿足。v1/v3=1/sinθ冷卻三角進口空氣阻力主要是由于翅片進口處發生的流體分離及后續混合引起。在翅片通道斷面1和斷面3處聯立動量方程和能量方程，并根據幾何相似原理進行適當推導和簡化，便可以得出阻力系數計算式(5)。

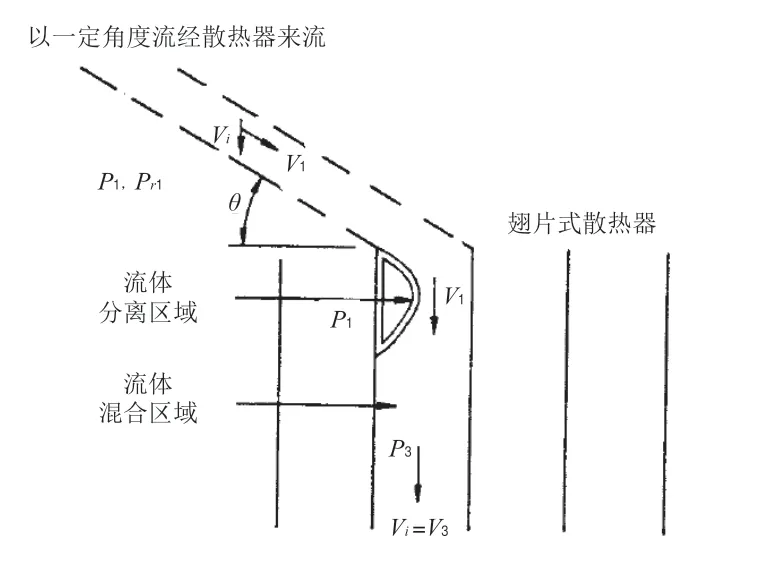
圖6 冷卻三角進口阻力產生機理示意圖

散熱器出口阻力系數計算式(7)的提出和推導基于以下現象：如圖7所示，離開單片冷卻柱的流體在另一片冷卻柱出流的相互干擾下，重新改變了流向。改變流向的過程也就是流場重建的過程，直到距離足夠遠，流場重新變得均勻穩定為止。

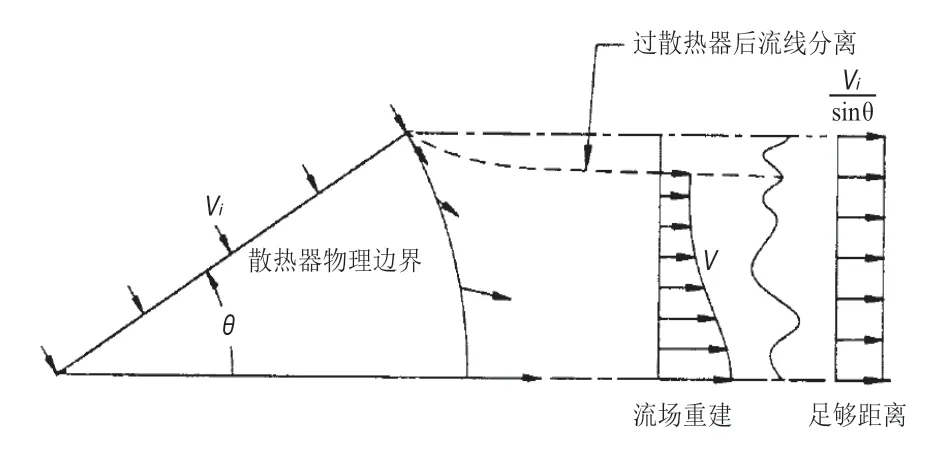
圖7 冷卻三角出口阻力產生機理示意圖

散熱器出口阻力的構成有兩部分，一部分是剛經過散熱器后轉向及沿三角頂部中心線發生的湍流衰減；另一部分是由相對穩定的中間狀態逐步彌合過渡到足夠遠處均勻流過程中產生的阻力。這部分阻力計算式(7)同樣采用了經驗公式進行估算，但頂角的適用范圍擴展至30～120°。

可知從流場和壓力分布來看，數模結果與電力工程水務設計手冊所選用公式的計算原理吻合較好，一定程度上驗證了設計手冊計算公式的合理性。

在迎風面上空氣剛進入翅片時，存在一個較明顯的總壓降低過程，對應圖6所示的流體近翅片出發生背離及后續彌合過程。

過散熱器后，流場及壓力場分布也如同圖7所示的情況類似，在冷卻三角頂部區域中心線上出現了明顯的低壓區域，并且隨著距離的增大，流場和壓力場均逐步趨于均勻。

4 結語與建議

火力發電廠間接空冷系統設計規范中散熱器進出口阻力系數計算公式為大量試驗數據基礎上擬合的經驗公式，使用時應特別注意校驗頂角是否屬于40°≤α≤70°的適用范圍。

電力工程水務設計手冊中散熱器進出口阻力系數計算公式為半理論半經驗公式，數值模擬結果驗證了相關公式的合理性，其適用范圍要更為寬泛一些。

除了冷卻三角頂角，冷卻三角進出口阻力還與散熱器幾何尺寸(如管束厚度和長度)、翅片間距、流場均勻性等因素有關，相關公式在具體工程中應用時可根據情況予以合理修正和調整。

將冷卻三角簡化為無厚度的散熱器模型，可能會造成散熱器進口阻力無法體現。應視模型要解決的問題決定是否對厚度進行簡化。對厚度簡化后，建議通過自定義函數增加相應的進出口阻力修正。

冷卻三角夾角大小對冷卻三角進出口阻力影響較大，在某些占地面積要求不是特別高的小型冷卻項目，可以考慮通過增加夾角角度，降低系統阻力進而獲得更大的通風能力和更好的冷卻效果。