基于POA-BP 的TP2 管材自由彎曲成形結(jié)果預(yù)測*

郝用興 張旭浩 劉亞輝

（①華北水利水電大學，河南 鄭州 450045；②河南省數(shù)字化智能裝備工程研究中心，河南 鄭州 450064）

彎管零件能夠從材料和結(jié)構(gòu)滿足產(chǎn)品輕量化、強韌化、低耗環(huán)保的需求，因此在航空、航天、船舶、汽車、醫(yī)療和能源等高技術(shù)產(chǎn)業(yè)得到了日益廣泛的發(fā)展和應(yīng)用[1]。

許多學者研究了管材彎曲過程中的起皺、管壁變薄、截面變形和回彈預(yù)測與控制等問題。田娥和劉婧瑤等[2-3]通過建立BP 神經(jīng)網(wǎng)絡(luò)有效預(yù)測彎管成形的回彈量；Zhang S 等[4]將管材三維回彈預(yù)測轉(zhuǎn)化為二維問題，建立了平面回彈前后半徑的數(shù)學關(guān)系，利用幾何連續(xù)性和修正函數(shù)進行補償，建立了可靠的三維變曲率管彎曲回彈預(yù)測數(shù)學模型；陳光耀等[5]使用RBF 神經(jīng)網(wǎng)絡(luò)預(yù)測管材數(shù)控（NC）彎曲的壁厚減薄率和回彈程度，并利用支持向量機（SVM）預(yù)測管材的起皺情況，從而實現(xiàn)了回彈的預(yù)測和成形質(zhì)量的提高；賈美慧等[6]通過粒子群算法優(yōu)化的RBF 神經(jīng)網(wǎng)絡(luò)實現(xiàn)了對管材彎曲的多目標工藝參數(shù)優(yōu)化；Wu J J 等[7]利用擴展卡爾曼濾波算法得出了管材成形的運動模型和觀測模型，最終預(yù)測了成形軌跡并優(yōu)化了加工參數(shù)，證明了加工優(yōu)化方案的有效性；趙陽等[8]構(gòu)建了MPSO-BP 神經(jīng)網(wǎng)絡(luò)預(yù)測模型，用于小半徑彎管成形結(jié)果的快速預(yù)測，并證明該模型的預(yù)測結(jié)果可靠有效。

目前針對管材自由彎曲的成形結(jié)果研究，徐振華等[9]通過解析法和有限元模擬相結(jié)合的方法預(yù)測管材自由彎曲的回彈數(shù)值，相較于傳統(tǒng)預(yù)測方式提升了11.08%的精度；Li Y S 等[10]的研究關(guān)注AL6061管材自由彎曲過程中的回彈現(xiàn)象，采用有限元和解析法進行研究，并通過添加中性層偏移來優(yōu)化管材彎曲回彈的解析模型。另外，對管材彎曲成形結(jié)果的有效預(yù)測可以幫助相關(guān)生產(chǎn)部門及時評估成形品質(zhì)的優(yōu)劣，并為選擇適當?shù)募庸?shù)提供有效的參考，對于推進自由彎曲成形技術(shù)的工程化具有重要意義。

本文選用外徑為12 mm，壁厚為1 mm 的TP2銅管，綜合采用理論分析、數(shù)值模擬和神經(jīng)網(wǎng)絡(luò)等方法。通過數(shù)值模擬建立樣本庫，并基于BP 神經(jīng)網(wǎng)絡(luò)建立管材自由彎曲成形結(jié)果的預(yù)測模型，使用鵜鶘優(yōu)化算法優(yōu)化預(yù)測模型的權(quán)值和閾值，提高預(yù)測精度，最終實現(xiàn)POA-BP 預(yù)測模型對TP2 管材三維自由彎曲成形結(jié)果的預(yù)測。

1 管材三維自由彎曲

圖1 所示為管材三維自由彎曲的成形簡圖。在未成形時，管材與各個成形構(gòu)件處于同一軸線上。開始成形時，管材在推進機構(gòu)的作用下，沿著Z軸方向移動，導(dǎo)向機構(gòu)在整個成形過程中對管材起著支撐的作用。球面軸承由兩個伺服電機驅(qū)動，實現(xiàn)在XY平面內(nèi)的自由移動，帶動彎曲模的偏移和旋轉(zhuǎn)。管材通過成形構(gòu)件的共同作用，在空間范圍內(nèi)實現(xiàn)自由彎曲。

圖1 管材三維自由彎曲成形簡圖

2 管材力學性能測試與自由彎曲有限元仿真

2.1 管材力學性能測試

為了準確地進行管材有限元仿真，需要獲取管材的力學性能參數(shù)，管材選擇?12 mm，壁厚1 mm的TP2 銅管。用專用夾具塞頭放置在管材兩端[11]，防止拉伸過程其變形。通過萬能試驗機對TP2 銅管進行3 次各向同性的拉伸試驗（圖2），取3 次試驗的平均值。經(jīng)過拉伸試驗后，得到的TP2 銅管的材料參數(shù)，見表1。

表1 TP2 銅管材料參數(shù)

圖2 拉伸試驗

管材彈性階段的本構(gòu)關(guān)系為

因為管材在彎曲成形過程中存在加工硬化現(xiàn)象，所以使用冪指數(shù)硬化模型來描述管材的塑性變形部分。

其中：b為TP2 銅管的初始屈服應(yīng)力。

TP2 管材的塑性階段采用冪指數(shù)硬化模型，并通過擬合曲線（圖3）表示。

圖3 σ-ε擬合曲線

2.2 管材自由彎曲有限元模擬

在Abaqus 有限元分析軟件中使用Abaqus/Explicit 求解器，建立了如圖4 所示的三維有限元模型來模擬管材的彎曲過程。為了提高仿真效率和結(jié)果準確性，設(shè)置了質(zhì)量縮放系數(shù)為25、摩擦系數(shù)為0.05，并采用通用接觸來模擬管材的彎曲成形過程。該模型中，管材被定義為可變形實體，并采用S4R 通用殼單元進行網(wǎng)格劃分。球面軸承、彎曲模、導(dǎo)向機構(gòu)和推進機構(gòu)則被定義為離散剛體。彎曲模部分采用C3D8R 單元進行網(wǎng)格劃分，而導(dǎo)向機構(gòu)等其他剛體模型則采用R3D4 單元進行網(wǎng)格劃分。各部件的網(wǎng)格劃分如圖5 所示。

圖4 管材自由彎曲有限元模型

圖5 各部件網(wǎng)格劃分

管材成形結(jié)果質(zhì)量的評價指標為管材壁厚減薄率δ和管材橢圓率ε為

式中：t為管材的初始壁厚；tmin為管材經(jīng)過彎曲后的最小壁厚。當管材的壁厚減薄率不超過10%時，即認為其質(zhì)量良好。

式中：Dmax表示管材經(jīng)過彎曲后的最大截面直徑；Dmin表示管材經(jīng)過彎曲后的最小截面直徑。在工業(yè)方面，銅管的橢圓率是要求不超過8%的。

3 數(shù)值模擬有效性驗證及訓練樣本和測試樣本生成

3.1 數(shù)值模擬有效性驗證

為了確保管材自由彎曲數(shù)值模擬和實際加工相吻合，需要對管材成形數(shù)值模擬進行驗證，以確保其有效性。

在有限元軟件中，設(shè)置推進機構(gòu)的推進速度為120 mm/s、導(dǎo)向機構(gòu)圓角半徑為2 mm、導(dǎo)向機構(gòu)與管材間隙為0.3 mm、彎曲模圓角半徑為2 mm、彎曲模與管材間隙為0.1 mm、彎曲變形區(qū)長度為24 mm、X軸的偏移量為0 mm、6 mm、0 mm，Y軸偏移量為5 mm、0 mm、7 mm，一共有3 個彎曲段。

在實際加工過程中，考慮到不可控因素，設(shè)置主要參數(shù)推進機構(gòu)的推進速度為120 mm/s，X軸和Y軸的偏移量與數(shù)值模擬一致。

最終的仿真結(jié)果和實驗結(jié)果如圖6 所示，兩者的幾何形狀較為吻合。3 個彎曲段的壁厚減薄率和橢圓率對比結(jié)果見表2，可以看出成形結(jié)果均符合評價指標，且這3 個彎曲段的最大壁厚減薄率偏差為0.64%，最大橢圓率偏差為1.15%，管材成形質(zhì)量較好，故管材成形數(shù)值模擬有效。

表2 模擬和實驗結(jié)果對比

圖6 模擬（上）與實驗（下）彎曲成形結(jié)果對比

3.2 訓練和預(yù)測樣本生成

相較于傳統(tǒng)的實驗加工方法，使用貼近實際加工的數(shù)值模擬可用于研究管材自由彎曲成形，同時也減少了物理實驗和成本的需求。基于經(jīng)過驗證的有限元仿真模型和工廠加工實際情況，最終確定彎曲模與管材間隙值A(chǔ)1、彎曲模圓角半徑值A(chǔ)2、管材彎曲變形區(qū)長度A3、導(dǎo)向機構(gòu)圓角半徑值A(chǔ)4、導(dǎo)向機構(gòu)與管材間隙值A(chǔ)5作為神經(jīng)網(wǎng)絡(luò)預(yù)測模型的輸入層節(jié)點。壁厚減薄率δ和橢圓率ε作為神經(jīng)網(wǎng)絡(luò)預(yù)測模型輸出層節(jié)點。

根據(jù)實際加工和數(shù)值模擬分析結(jié)果，確定以下主要影響因素的取值范圍為：彎曲模與管材間隙值A(chǔ)1為0.1～0.3 mm、彎曲模圓角半徑值A(chǔ)2為1.5～2.5 mm、管材彎曲變形區(qū)長度A3為21～25 mm、導(dǎo)向機構(gòu)圓角半徑值A(chǔ)4為1.5～2.5 mm、導(dǎo)向機構(gòu)與管材間隙值A(chǔ)5為0.2～0.4 mm，其他參數(shù)根據(jù)實際加工情況進行設(shè)定。

根據(jù)影響因素的取值范圍分散選取36 組加工參數(shù)，通過數(shù)值模擬對36 組加工參數(shù)進行成形，從中隨機選取6 組作為測試樣本，剩下的30 組作為訓練樣本。

4 POA-BP 神經(jīng)網(wǎng)絡(luò)預(yù)測模型

4.1 BP 神經(jīng)網(wǎng)絡(luò)及鵜鶘優(yōu)化算法

4.1.1 BP 神經(jīng)網(wǎng)絡(luò)

人工神經(jīng)網(wǎng)絡(luò)可處理多變量非線性優(yōu)化問題并逼近任何函數(shù)。BP 神經(jīng)網(wǎng)絡(luò)是一種具有多層節(jié)點的前饋神經(jīng)網(wǎng)絡(luò)，它使用誤差逆向傳播算法來進行訓練，它具有良好的非線性函數(shù)逼近能力和時變性，常用于處理多變量非線性優(yōu)化問題，網(wǎng)絡(luò)拓撲結(jié)構(gòu)包括輸入層、隱含層和輸出層，且三層或以上的結(jié)構(gòu)可以逼近大多數(shù)的非線性函數(shù)[12]，如圖7 所示。

圖7 BP 神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)

由于BP 神經(jīng)網(wǎng)絡(luò)學習訓練開始時，網(wǎng)絡(luò)的結(jié)構(gòu)參數(shù)是隨機給定的，會出現(xiàn)網(wǎng)絡(luò)的收斂速度較慢、不穩(wěn)定且容易陷入局部最小值的困境，導(dǎo)致最大相對誤差存在，從而影響網(wǎng)絡(luò)的性能和預(yù)測準確性。

4.1.2 鵜鶘優(yōu)化算法

鵜鶘優(yōu)化算法（pelican optimization algorithm，POA）是由Pavel Trojovsky和Mohammad Dehghani在2022 年提出的[13]，該算法模擬了鵜鶘在狩獵過程中的自然行為，通過模擬鵜鶘鳥在覓食過程中的搜索策略和動態(tài)調(diào)整能力，來解決優(yōu)化問題，如圖8 所示。該算法將優(yōu)化問題轉(zhuǎn)化為參數(shù)搜索的過程。在算法的迭代過程中，每個鵜鶘個體代表一個解，根據(jù)當前解的適應(yīng)度值進行搜索和更新，通過合作與信息共享，個體之間共同尋找最優(yōu)解。通過不斷迭代搜索和位置調(diào)整，鵜鶘優(yōu)化算法能夠逐漸收斂到全局最優(yōu)解，為解決實際問題提供了一種高效而靈活的優(yōu)化方法。

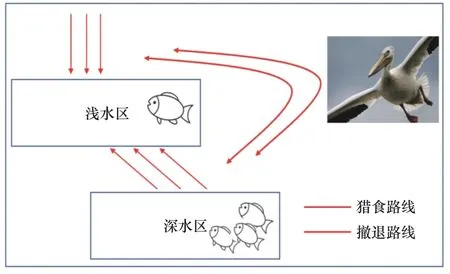
圖8 鵜鶘捕獵的方式

鵜鶘優(yōu)化算法是模擬鵜鶘在攻擊和捕獵獵物時的行為和策略，以更新候選解，該狩獵策略分為探索和開發(fā)兩個階段進行模擬，其數(shù)學模型如下：

（1）初始化

鵜鶘種群初始化數(shù)學描述如下：

式中：xi,j為第i個鵜鶘的第j維的位置；N為鵜鶘的種群數(shù)量；m為求解問題的維度；rand是[0,1]范圍內(nèi)的隨機數(shù)；uj和lj分別是求解問題的第j維的上下邊界。

在鵜鶘優(yōu)化算法中，求解問題的目標函數(shù)可以用來計算鵜鶘的目標函數(shù)值；鵜鶘種群的目標函數(shù)值用向量表示為

式中：F為鵜鶘種群的目標函數(shù)向量；Fi為第i個鵜鶘的目標函數(shù)值；Xi表示為為第i個鵜鶘的位置。

（2）逼近獵物（探索階段）

在探索階段，鵜鶘確定獵物位置并向其移動，通過對鵜鶘策略建模，掃描搜索空間并利用POA發(fā)現(xiàn)不同區(qū)域。該算法的關(guān)鍵是獵物位置在搜索空間中隨機生成，增強了精確搜索的能力。這些概念和鵜鶘的移動策略可以用數(shù)學模型式（7）來表示。

（3）水面飛行，捕捉獵物（開發(fā)階段）

在開發(fā)階段，當鵜鶘達到水面時，展開翅膀驅(qū)趕獵物向上移動，并將其收集在喉袋中。這種策略使更多的獵物在攻擊區(qū)域被捕獲。通過對鵜鶘行為建模，POA 能更好地收斂到狩獵區(qū)域的優(yōu)質(zhì)點，提高了本地搜索和開發(fā)能力。算法需要檢查鵜鶘周圍的點，以找到更好的解。鵜鶘的捕獵行為可以通過式（8）進行數(shù)學模擬。

經(jīng)過上述的搜索和捕獲過程后，鵜鶘會再次攻擊和捕獵，即進行迭代計算。不斷更新最優(yōu)位置，鵜鶘群需要不斷地進行位置更新。根據(jù)上述得到的設(shè)計變量和目標函數(shù)值的新選擇，用新得到的最優(yōu)位置替換原來的最優(yōu)位置，然后繼續(xù)迭代計算，直到找到最優(yōu)解。迭代停止并輸出最終的計算結(jié)果。

4.1.3 POA-BP 預(yù)測模型設(shè)計

根據(jù)BP 神經(jīng)網(wǎng)絡(luò)和鵜鶘優(yōu)化算法的數(shù)學模型，建立管材自由彎曲成形結(jié)果預(yù)測模型的步驟如下。

（1）通過Mapminmax函數(shù)對管材自由彎曲成形結(jié)果和輸入?yún)?shù)進行歸一化處理。利用標準BP 神經(jīng)網(wǎng)絡(luò)建立預(yù)測模型，并設(shè)定學習速率、學習目標、最大迭代次數(shù)、動量因子和激活函數(shù)。根據(jù)經(jīng)驗公式（9），選擇適當數(shù)量的隱含層節(jié)點來確定BP 神經(jīng)網(wǎng)絡(luò)的拓撲結(jié)構(gòu)[14]。

式中：w為隱含層節(jié)點數(shù)；n為輸入層節(jié)點數(shù)；v為輸出層節(jié)點數(shù)；z為1～10 的常數(shù)。

（2）初始化鵜鶘種群規(guī)模N、最大迭代次數(shù)T、搜索空間維度m等基本參數(shù)。管材自由彎曲成形結(jié)果預(yù)測模型中自變量的個數(shù)o為

（3）將BP 神經(jīng)網(wǎng)絡(luò)的權(quán)重和閾值作為鵜鶘個體的參數(shù)。對于每個個體，隨機初始化權(quán)重和閾值，并將其作為解的一部分。BP 神經(jīng)網(wǎng)絡(luò)的均方誤差（MSE）作為鵜鶘優(yōu)化算法的適應(yīng)度函數(shù)，表示為

式中：F為適應(yīng)度函數(shù)；Tq為第q項值的期望輸出，q=1,···,e，e為訓練樣本總數(shù)；為第q項值第p次迭代后的網(wǎng)絡(luò)輸出；H為總迭代次數(shù)，p=1,···,H。

根據(jù)上述公式計算得到最優(yōu)鵜鶘個體捕捉獵物的位置，并將其存儲在Xi中。

（5）將最佳結(jié)果的值賦予BP 神經(jīng)網(wǎng)絡(luò)的權(quán)重和閾值，通過這些優(yōu)化后的權(quán)值和閾值再次訓練神經(jīng)網(wǎng)絡(luò)，直至達到目標精度或是最大迭代次數(shù)。

（6）通過步驟（5）得到的管材自由彎曲成形結(jié)果預(yù)測模型，輸入新的數(shù)據(jù)即可完成成形結(jié)果的預(yù)測。

4.2 管材成形結(jié)果預(yù)測模型建立

4.2.1 BP 神經(jīng)網(wǎng)絡(luò)預(yù)測模型

根據(jù)3.2 節(jié)建立的訓練和預(yù)測樣本，構(gòu)建3 層拓撲結(jié)構(gòu)的BP 神經(jīng)網(wǎng)絡(luò)，輸入層節(jié)點數(shù)為5，輸出層節(jié)點數(shù)為2，隱含層采用tansing 激活函數(shù)，輸出層采用purelin 激活函數(shù)，采用梯度下降動量和自適應(yīng)學習率算法traingdx 進行訓練，目標誤差為0.000 1，學習率為0.05，動量因子為0.4，最大迭代次數(shù)為800。由式（10）可以得出隱含層節(jié)點數(shù)的可能取值范圍為4～13，依次將不同的隱含層節(jié)點數(shù)代入訓練計算得出均方誤差，結(jié)果見表3，可知當隱含層節(jié)點數(shù)為13 的時候，訓練誤差取得最小值，故5-13-2 拓撲結(jié)構(gòu)下的BP 神經(jīng)網(wǎng)絡(luò)的預(yù)測精度最高。

表3 不同隱含層節(jié)點數(shù)訓練得到的MSE

為了深入研究具有穩(wěn)定性和收斂速度快的預(yù)測模型，避免BP 神經(jīng)網(wǎng)絡(luò)陷入局部最優(yōu)解，需要對該BP 模型進行改進。

4.2.2 POA-BP 神經(jīng)網(wǎng)絡(luò)預(yù)測模型

根據(jù)4.2.1 小節(jié)確定的BP 神經(jīng)網(wǎng)絡(luò)拓撲結(jié)構(gòu)和查閱相關(guān)資料，設(shè)置鵜鶘優(yōu)化算法的基本參數(shù)見表4。

表4 鵜鶘優(yōu)化算法基本參數(shù)

通過30 組訓練樣本對POA-BP 神經(jīng)網(wǎng)絡(luò)進行訓練，建立POA-BP 神經(jīng)網(wǎng)絡(luò)預(yù)測模型，對6 組預(yù)測樣本進行預(yù)測，與BP 預(yù)測模型的結(jié)果進行對比，如表5 和圖9 所示，可知POA-BP 預(yù)測模型的壁厚減薄率誤差I(lǐng)t和橢圓率誤差I(lǐng)d最大不超過2%；另外，POA-BP 預(yù)測模型的決定系數(shù)高達0.998 54 和0.997 37，不僅高于BP 神經(jīng)網(wǎng)絡(luò)且更接近于1，故該神經(jīng)網(wǎng)絡(luò)模型的預(yù)測準確性和擬合性能均優(yōu)于BP 神經(jīng)網(wǎng)絡(luò)。

表5 BP 模型、POA-BP 模型的預(yù)測結(jié)果與數(shù)值模擬結(jié)果對比

圖9 數(shù)值模擬、BP 預(yù)測模型、POA-BP 預(yù)測模型結(jié)果對比圖

4.2.3 POA-BP 預(yù)測模型實驗對比驗證

由于本文神經(jīng)網(wǎng)絡(luò)的訓練樣本是基于數(shù)值模擬的，所以為了驗證POA-BP 預(yù)測模型在管材實際加工過程中的有效性，將隨機選取的6 組預(yù)測樣本的加工參數(shù)通過管材三維自由彎曲成形設(shè)備進行實驗，并使用手持式三維掃描儀對成形后的管材進行掃描和后處理，以測量其各參數(shù)值，如圖10 所示。將成形后的結(jié)果與POA-BP 預(yù)測模型的結(jié)果進行對比，結(jié)果見表6。

表6 實際加工與POA-BP 預(yù)測模型結(jié)果對比

圖10 實驗設(shè)備

從表6 可以看出，POA-BP 模型的預(yù)測結(jié)果與實際加工的成形結(jié)果吻合度較好，說明POA-BP 模型可以有效地預(yù)測實際加工的成形結(jié)果，也進一步驗證了數(shù)值模擬的有效性。

5 結(jié)語

（1）管材的加工參數(shù)和成形結(jié)果之間沒有直接的函數(shù)關(guān)系，因此增加了準確預(yù)測管材成形結(jié)果的難度。在實際管材加工中，準確預(yù)測成形結(jié)果對生產(chǎn)部門至關(guān)重要。它能幫助生產(chǎn)部門及時評估成形結(jié)果的質(zhì)量，并為選擇合適的加工參數(shù)提供有價值的指導(dǎo)。

（2）通過鵜鶘優(yōu)化算法優(yōu)化后的BP 神經(jīng)網(wǎng)絡(luò)模型具有更高的收斂性能、更好的擬合程度、更強的穩(wěn)定性能，有效地改善了標準BP 神經(jīng)網(wǎng)絡(luò)容易陷入局部最優(yōu)解的問題；研究表明，POA-BP 預(yù)測模型的壁厚減薄率和橢圓率的最大誤差不超過2%，故采用POA-BP 神經(jīng)網(wǎng)絡(luò)模型可以準確地預(yù)測管材自由彎曲的成形結(jié)果。

（3）通過對6 組預(yù)測樣本進行實際加工并與預(yù)測模型結(jié)果對比，驗證了POA-BP 預(yù)測模型在管材自由彎曲成形預(yù)測方面的實際價值。