一種分布式電推進飛機的多學科參數快速估計方法

于昊亮，雷濤，張星雨，張曉斌

西北工業大學 飛機電推進技術工業和信息化部重點實驗室，陜西 西安 710072

飛機電推進系統是指采用電能作為能量主體的飛機推進系統，包含全電、混合電推進技術和分布式電推進技術。電推進飛機所采用的能源形式有太陽光伏、燃料電池、蓄電池、油電混合等[1]，推進方式有集中式和分布式，推進器有電動螺旋槳和涵道風扇。在飛機電推進技術的諸多概念中，分布式電推進（DEP）技術是目前的研究熱點之一[2-3]。

近年來，隨著分布式電推進概念的日益普及和應用于航空的推進電機技術的快速發展，出現了各種新的飛機概念設計方案。由于受到電源的能量密度等技術的限制，大部分都是中小型飛機的概念設計方案。分布式電推進技術可以應用于常規布局飛機（e-CTOL）、短距起降飛機（e-STOL），以及垂直起降飛機（e-VTOL）中，每一類飛機都面向不同的應用市場。

將分布式電推進技術應用到飛行器設計中，會使飛行器的氣動特性與推進系統之間強烈耦合，需要從更多的角度挖掘出其氣動—推進耦合特性。基于工程經驗的飛機總體設計思路和氣動設計分析方法不再適用于分布式電推進布局飛行器的早期設計。

國內外很多學者開展了分布式電推進飛機的相關研究。王科雷等[4]研究了太陽能無人機的分布式螺旋槳與機翼氣動耦合特性，基于多參考系模型（MRF）求解雷諾平均方程（RANS），進行了高精度的準定常數值模擬，螺旋槳滑流使機翼升阻力增大、升阻比減小，并且可以延緩流動分離。楊小川等[5-6]基于激勵盤理論，研究了分布式螺旋槳在多種不同的轉向組合下，其滑流效應對機翼及整機氣動特性的影響。楊偉等[7]采用激勵盤模型及量子粒子群優化算法對考慮滑流影響下的分布式螺旋槳布局進行了氣動優化設計研究，驗證了此分析方法是可行且有工程利用價值的。饒崇等[8]對一種分布式電推進飛機的低速特性進行了數值求解，驗證了滑流增升以及翼尖減阻的結論。成志勇等[9]基于渦格法建立了一種分布式電推進飛機的氣動特性快速評估方法，并用高精度求解方法對其進行了驗證。雷瑤等[10]推導了旋翼與機翼相互干擾時的氣動模型，并通過對比數值模擬與風洞試驗的結果得到了不同旋翼位置對DEP氣動性能的影響。美國斯坦福大學使用Python語言搭建環境，并對分布式電推進飛機進行了分析[11]與優化[12]。馬一元等基于一架裝有24 個電動涵道風扇的分布式電推進無人驗證機確立了一種分布式電推進飛機的總體設計方法[13]及多學科優化設計方法[14]。張星雨等對分布式電推進無人驗證機依次開展了地面車載試驗研究[15]及風洞試驗研究[16]，初步得到了一些分布式電推進飛機氣動—推進耦合特性的基本規律。

目前，絕大多數對分布式電推進構型的研究集中在通過數值仿真或試驗來研究氣動—推進耦合特性上，還沒有特別好的方法對分布式電推進飛機進行多學科參數快速估計。主要原因是分布式電推進構型復雜度高，涉及的參數比較多，常規的模型分析及優化設計方法需要的代價很大。因此，需要針對此問題發展快速有效的優化手段和設計工具。

針對上述問題，本文提出對分布式電推進飛機進行多學科參數快速估計的基本方法并搭建電動飛機多學科分析框架；建立螺旋槳—機翼簡化氣動分析模型，并與風洞試驗結果進行對比驗證；綜合考慮氣動—推進耦合特性及電推進系統的性能，以典型的分布式電推進飛機為例，進行多學科參數快速估計，分析整個飛行剖面下的飛機氣動性能變化及電推進系統的性能變化。該方法適用于總體方案論證階段。

1 電動飛機多學科分析框架

1.1 總體框架

電動飛機與常規飛行器最大的區別在于能源框架的不同，所以針對電動飛機，本文建立新的能源系統框架。電動飛機總體建模的框架如圖1所示。

1.2 電推進系統的建模

為電動飛機提供動力的所有部件組合被稱為飛機的電推進系統。全電飛機的能源系統框架比較簡單，由電池、電機、電機調速器、螺旋槳組成[17]。其框架示意圖如圖2所示。圖中綠色線表示電能，紅色線表示機械能，電機將電能轉化為機械能，并帶動螺旋槳旋轉。

1.2.1 鋰離子電池放電模型

任何電推進系統的核心都是能源，可以是電池、燃料電池或通過發電機產生電能。對于典型的鋰離子電池，采取基于經驗的電池放電模型

式中，f表示電池放電程度的度量；x為電池的放電狀態；R0為基準內阻；R為電池的內阻，隨著電池的放電而發生變化；C為電池的放電倍率；I為電池的電流；Pdischarge為電池的放電功率。

1.2.2 電機模型

在飛機總體設計階段，需要對電動通航飛機的全機性能進行分析，該階段是對飛機的初步設計方案進行論證，故可以使用各部件簡化的低階模型，提高早期的設計迭代效率。可以將推進電機近似建模為無刷直流電機模型，并忽略溫度等因素對電機性能的影響。本文采用一個經驗修正的一階模型來分析無刷直流電機的性能。該模型詳細介紹了無刷直流電機的等效內部電路模型，如圖3所示。

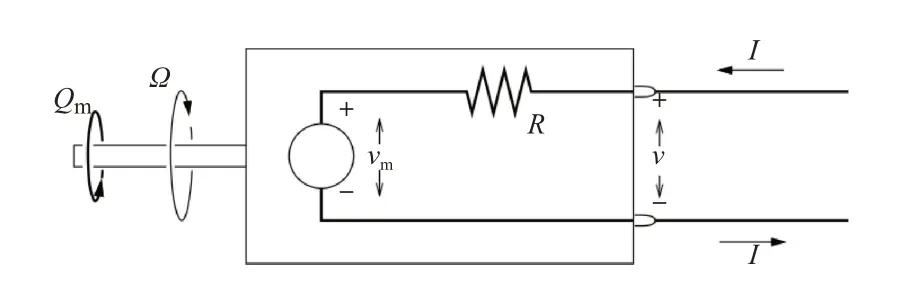
圖3 直流電機的等效電路圖Fig.3 Equivalent circuit for a DC electric motor

圖3 中，Qm為電機的轉矩；Ω為電機的轉速；vm為電機內部的反電動勢；R為電機的電阻；v為電機的端電壓；I為通過的電流。

假設電機的電阻R是定值，軸扭矩與電流成線性關系

式中，KQ是電機的轉矩常數。

假設電機內部的反電動勢等于電機轉速與電機速度常數之比，進而得到電機的端電壓

根據上述公式，可以得到電機的電流i、轉矩Qm、軸功率Pshaft及效率ηm，它們都是電機轉速Ω和端電壓v的函數

1.2.3 螺旋槳模型

螺旋槳的幾何相對復雜，將一種螺旋槳快速最優設計方法[18]編寫成螺旋槳設計函數，以達到快速建模及多學科參數估計的目的。在程序中輸入螺旋槳的設計層面參數，進而得到螺旋槳沿半徑的弦長分布和扭轉分布，確定螺旋槳的幾何模型，由此程序快速生成一個4葉螺旋槳，其三維模型在開源飛行器設計軟件OpenVSP 中可視化，如圖4所示。

圖4 螺旋槳模型在OpenVSP中可視化Fig.4 Propeller model displayed in OpenVSP

再使用葉素動量理論（BEM）來計算螺旋槳的性能參數，由于該方法的計算速度較快且滿足一定精度，很適用于在飛行器總體設計階段使用[19]。先求得不同站位葉素的推力和扭矩，再沿著徑向進行積分，以獲得螺旋槳的推力和扭矩，如式（11）和式（12）所示

1.3 飛行剖面任務段的建模

為分析電動飛機在整個飛行剖面上的性能，對飛行剖面各任務段進行建模。通過簡化各任務段的飛行狀態，分析飛機爬升、下降、巡航等飛行狀態的性能，構建詳細的飛行剖面圖。

在總體設計階段，考慮迭代效率，可以將飛行剖面簡化為二維模型，在此基礎上，基于飛行動力學基本原理完成整個飛行剖面的建模。

電動飛機的巡航階段可以被簡化建模為在恒定高度以恒定的速度飛行。巡航階段的求解輸入包括水平飛行速度、飛行高度、巡航的航程、飛機巡航的初始質量和初始時間，飛機巡航段的結束時間可以通過航程和速度來計算。

在巡航階段中，可以假設飛機的加速度為零。在恒定高度下，基于上述輸入，可以計算飛機在巡航條件下的升力、阻力及推力，并作為電推進系統性能評估的輸入參數，形成完整的迭代求解。

電動飛機的爬升和下降階段可以被簡化建模為爬升率恒定的飛行階段，飛機爬升時，爬升率為正數；飛機下降時，爬升率為負數。爬升和下降階段的輸入包括初始高度、結束高度、初始速度、結束速度和爬升率。而對于起飛和降落階段，則需要考慮地面對飛機的支持力及摩擦力，再根據飛機的實時狀態，建立力的平衡方程，形成完整的迭代求解。常規電動飛機的飛行剖面示意圖及各任務段的具體含義分別如圖5（1ft≈0.3048m）和表1所示。

表1 飛行剖面含義Table 1 Meaning of flight profile

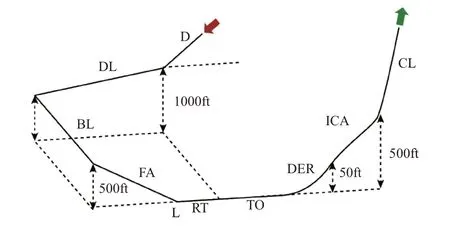
圖5 典型的飛行剖面Fig.5 Typical flight profile

1.4 氣動分析方法簡述

螺旋槳與機翼的簡化氣動耦合特性分析模型由螺旋槳槳葉渦系、螺旋槳尾跡渦系、機翼翼面渦系及源匯系和機翼尾跡渦系4個基本模型疊加而成，見表2。

表2 螺旋槳/機翼的氣動—推進耦合分析模型Table 2 Propeller/wing aero-propulsion coupling model

渦格法（VLM）則是升力面理論的數值解法。渦格法在求解這一類問題時具有較高的精度，同時計算的復雜性降低，大大減小了計算成本。

渦格法的數學本質為均勻流與三維渦線兩種簡單位勢流的疊加，在滿足亥姆霍茲定理的條件下，將機翼近似為一個曲面，將機翼沿展向和弦向進行離散，在構成的格子中布置馬蹄渦，利用Biot-Savart 定律計算位于每個格子弦的控制點處的所有馬蹄渦所誘導的速度，渦格法的示意圖如圖6所示，馬蹄渦示意圖如圖7所示。

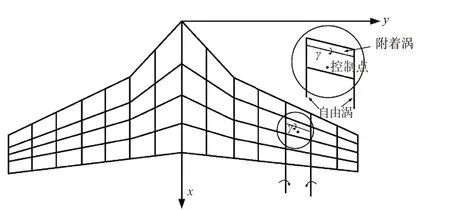
圖6 渦格法原理示意圖Fig.6 The principle of the vortex lattice method

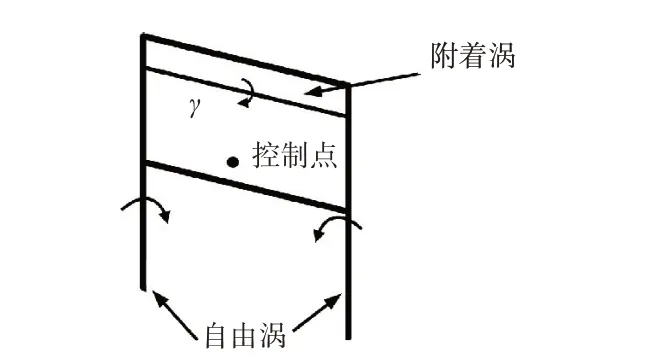
圖7 馬蹄渦示意圖Fig.7 Horseshoe vortex diagram

對于螺旋槳，通過基于勢流理論的螺旋尾流模型，將螺旋槳的尾流建模為渦環。渦環元素呈平面或四邊形，由四面強度相同的邊界渦絲組成。每個環引起的總速度可以用VLM中描述的方法計算，先計算4個單獨的渦絲的影響，再進行疊加，可以得到一個渦環的誘導速度。從而可以進一步將渦環強度與機翼的離散馬蹄渦進行疊加，可近似模擬螺旋槳滑流對機翼的影響。

在機翼第m個渦格控制點總的渦誘導速度vtotm滿足

式中，vwingm為在此控制點的機翼馬蹄渦的誘導速度，vwakem為在此控制點的螺旋槳尾流渦環的誘導速度。

式中，N為升力面上渦格的總數；Cm,n是影響系數矩陣，它取決于第n個馬蹄渦的幾何形狀及其與第m個渦格的控制點的距離；Cr,t是基于初始條件構造的渦環系統的影響矩陣，取決于初始徑向位置r和時間步長t。

2 快速氣動評估方法的算例驗證

為了驗證所使用的簡化氣動模型的求解準確性，將簡化方法得到的氣動結果與風洞試驗數據進行對比驗證。

2.1 算例模型簡述

本文以具有風洞試驗數據的PROWIM 模型[20]作為算例進行方法驗證。平直機翼的展弦比為5.33，翼型為NACA642-A015，半翼展長度為0.64m。螺旋槳具有4個槳葉，直徑為0.236m，螺旋槳由短艙內的5.5kW 的電機驅動。模型的俯視圖如圖8所示。

圖8 PROWIM模型俯視圖及尺寸（單位：mm）Fig.8 PROWIM model top view and dimensions(Unit: mm)

氣動分析的工況條件為：雷諾數Re= 8 × 105，自由來流馬赫數Ma= 0.15。螺旋槳的前進比取0.81進行分析。

2.2 算例驗證結果分析

簡化的氣動分析方法的分析結果與風洞試驗得到的在不同迎角下的升力系數的數據對比如圖9所示。

圖9 簡化分析結果與試驗數據的對比Fig.9 Comparison of the results of the simplified analysis with the experimental data

3 全飛行剖面的多學科分析

基于前文建立的電推進飛機的多學科分析模型以及對簡化的氣動—推進耦合模型的算例驗證結果，本節將在一個典型的飛行剖面下，對一架分布式電推進飛機進行多學科的參數快速估計。

建立如圖10 所示的分布式電推進飛機，機翼為平直翼，翼展為9.6m，弦長為1.6m，展弦比為6，翼型為NACA2412，在機翼前緣安裝8個分布式螺旋槳。飛行器的機身、垂尾和平尾的幾何參數均與Tecnam P2006T 飛機保持一致。

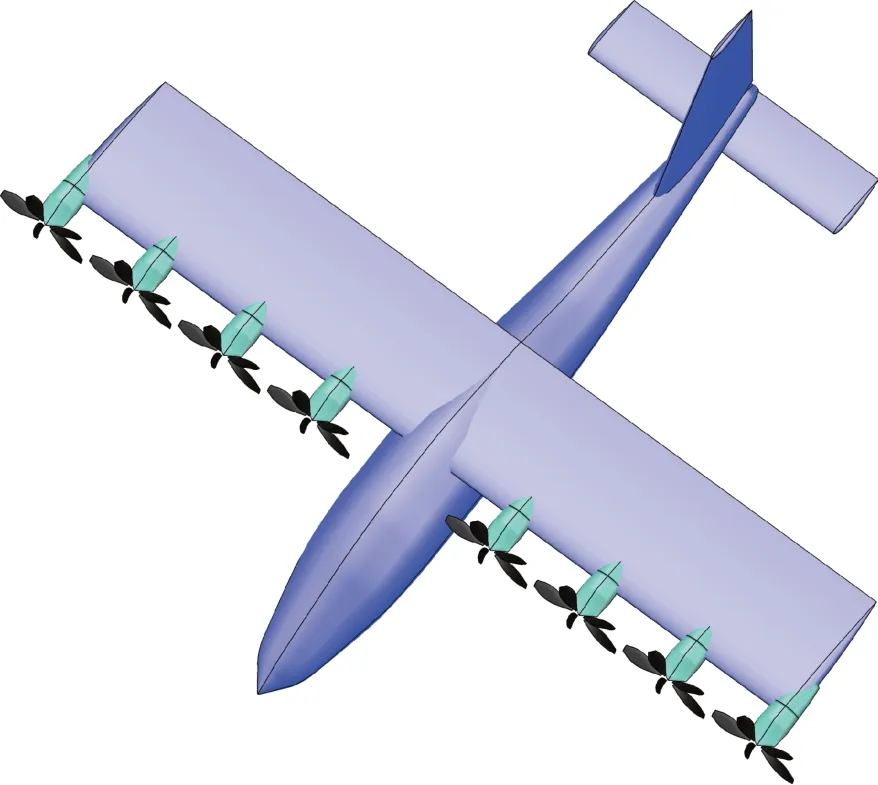
圖10 典型的分布式電推進飛機示意圖Fig.10 A typical distributed electric propulsion aircraft

由于電動飛機在飛行過程中的重量不變，可以得到針對電動飛機航程R的近似估算方法[21]

式中，Ebat為電池的能量密度；mbat為電池質量；mtot為起飛質量；η為電源及推進系統的傳動效率。

根據式（15），可以初步確定一些飛行器的總體參數。根據經驗，初步可以取通用航空飛機的升阻比L/D= 14，電源及推進系統的傳動效率η= 0.75，而近日寧德時代發布的凝聚態電池的單體能量密度可以達到500W·h/kg，故本文取鋰離子電池電芯的能量密度為350W·h/kg，認為這是未來5 年可以達到的技術水準。需要注意的是，式（15）是在飛機巡航狀態求得的航程估算公式，實際的航程會偏低一些，初步取R= 450km。

設定飛機的起飛質量為1500kg，則由式（13）可求得電池質量的500kg。表3 給出了飛行剖面各任務段的詳細參數信息。

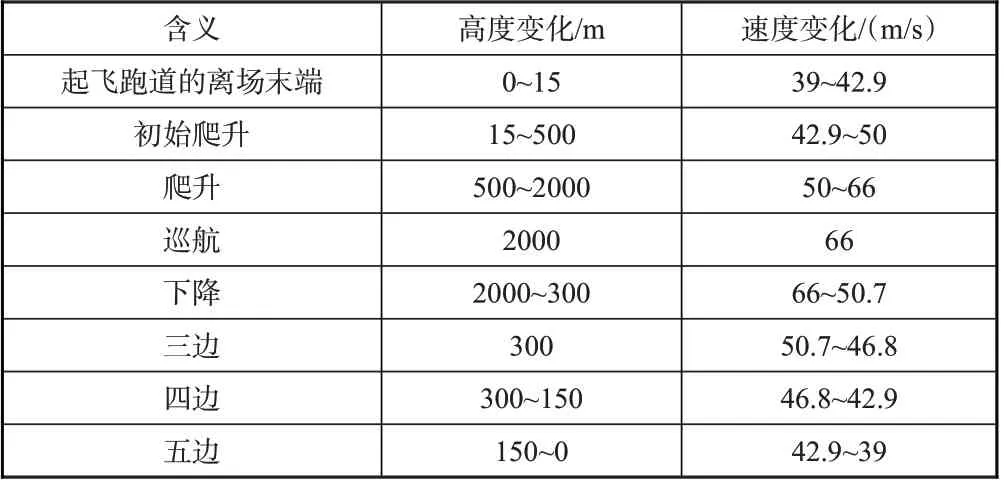
表3 飛行剖面各任務段的參數設置Table 3 Parameter settings of each segment of the flight profile

對其整個飛行剖面進行仿真，飛機的飛行高度隨時間的變化曲線如圖11 所示。在整個飛行剖面下的飛機飛行速度隨時間的變化曲線如圖12 所示。升阻比隨時間的變化曲線如圖13 所示，在巡航工況下，飛機全機的升阻比約為13.7，可以在飛行器的初步設計中將66m/s 作為遠航速度，巡航迎角為4.6°。

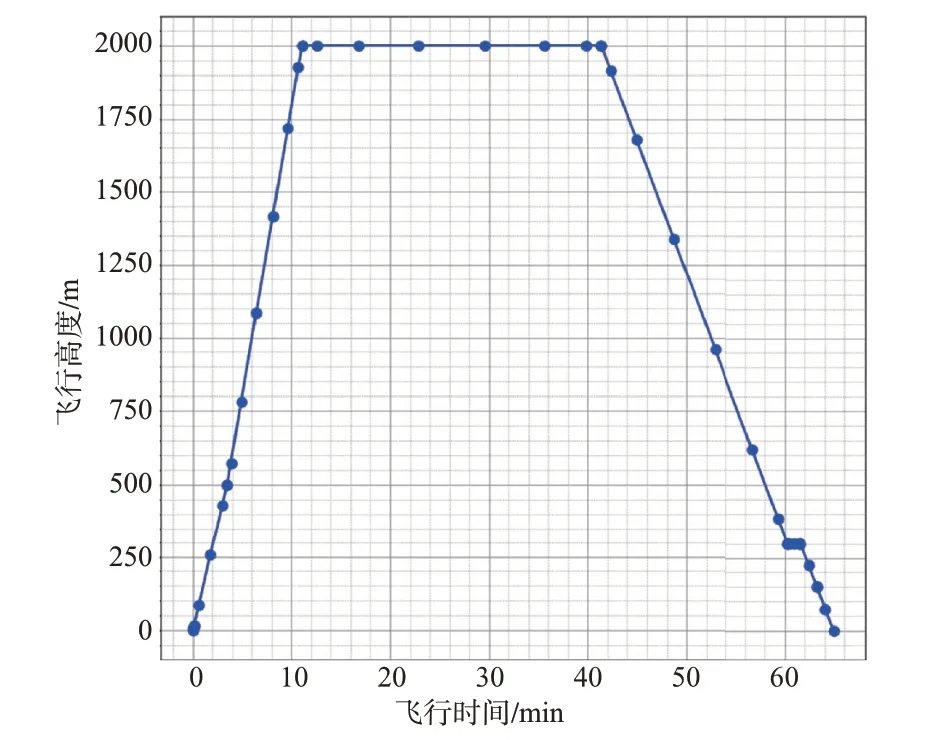
圖11 飛機飛行高度隨時間的變化曲線Fig.11 Curve of flight altitude over time

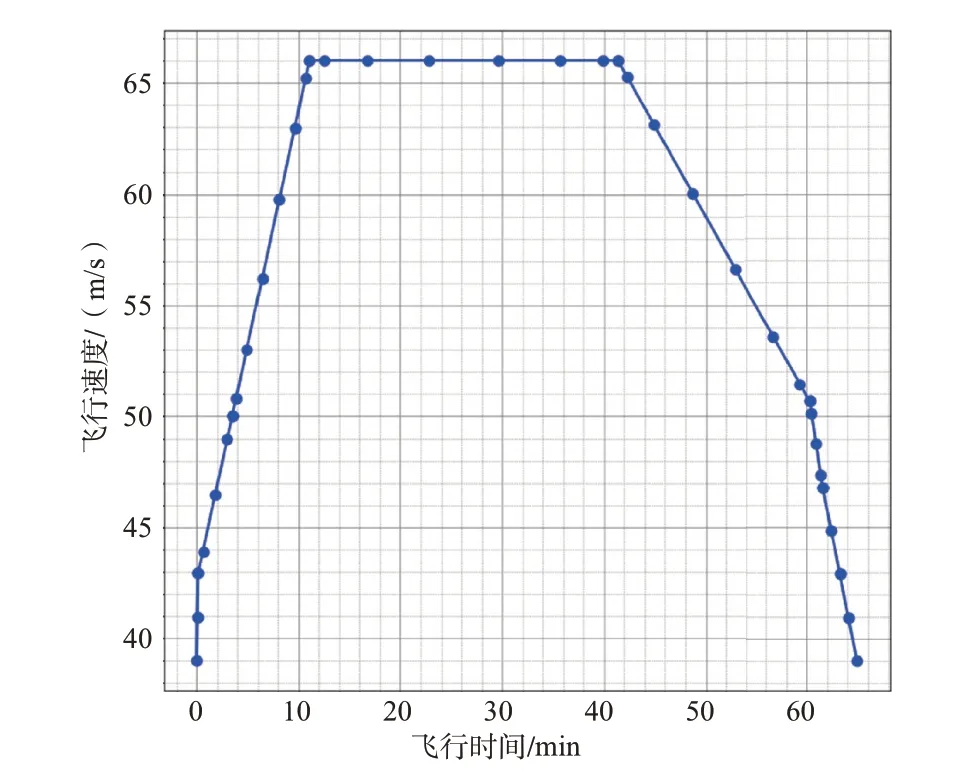
圖12 飛機飛行速度隨時間的變化曲線Fig.12 Curve of flight speed over time

圖13 升阻比隨時間的變化曲線Fig.13 Curve of lift-to-drag ratio changing with time

圖14～圖18 為螺旋槳和電機相關的性能分析結果，均在整個飛行剖面下進行分析。其中，圖14為多個螺旋槳的總推力變化曲線，圖15 為螺旋槳的轉速變化曲線，圖16 為螺旋槳的扭矩變化曲線，圖17 為螺旋槳的效率曲線，圖18為電機的效率曲線。從圖中可以看出，在起飛和爬升狀態時，螺旋槳的推力值較大，轉速較高，扭矩值較大，螺旋槳效率和電機效率均較低；在巡航狀態時，推力減小，轉速穩定值略高于1080r/min，扭矩穩定值略高于90N·m，螺旋槳的效率約為0.85，電機效率約為0.95。

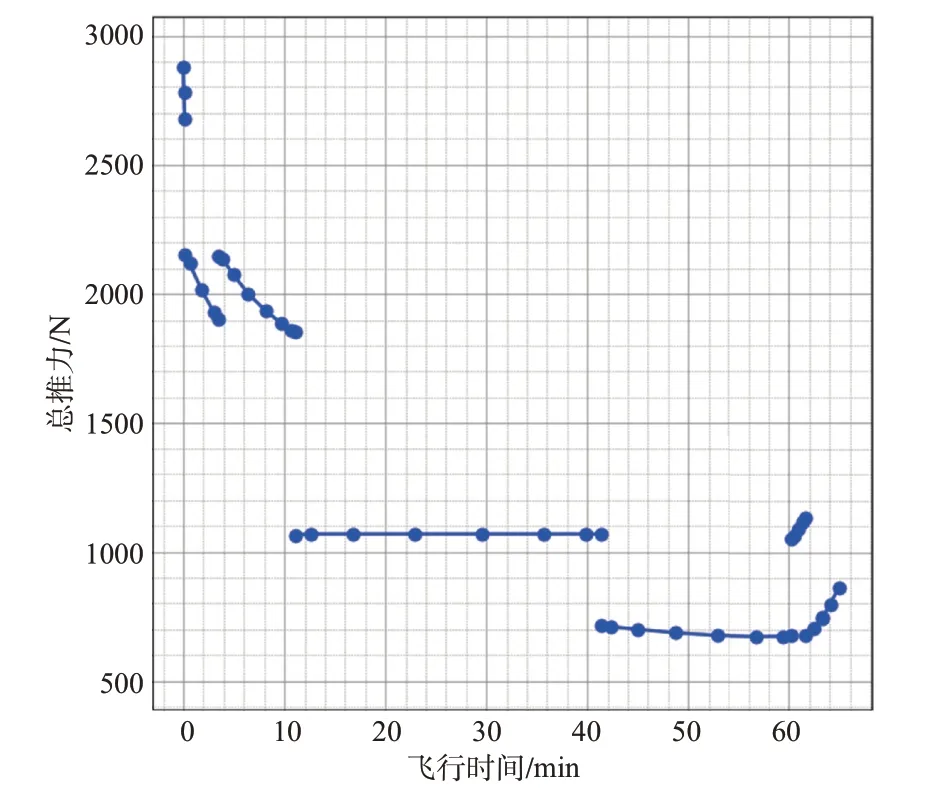
圖14 多個螺旋槳的總推力變化曲線Fig.14 Total thrust curve of multiple propellers

圖15 螺旋槳的轉速變化曲線Fig.15 RPM curve of the propeller

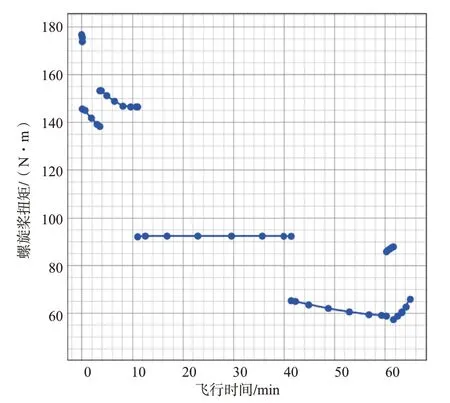
圖16 螺旋槳的扭矩變化曲線Fig.16 Torque curve of the propeller

圖17 螺旋槳效率曲線Fig.17 Propeller efficiency

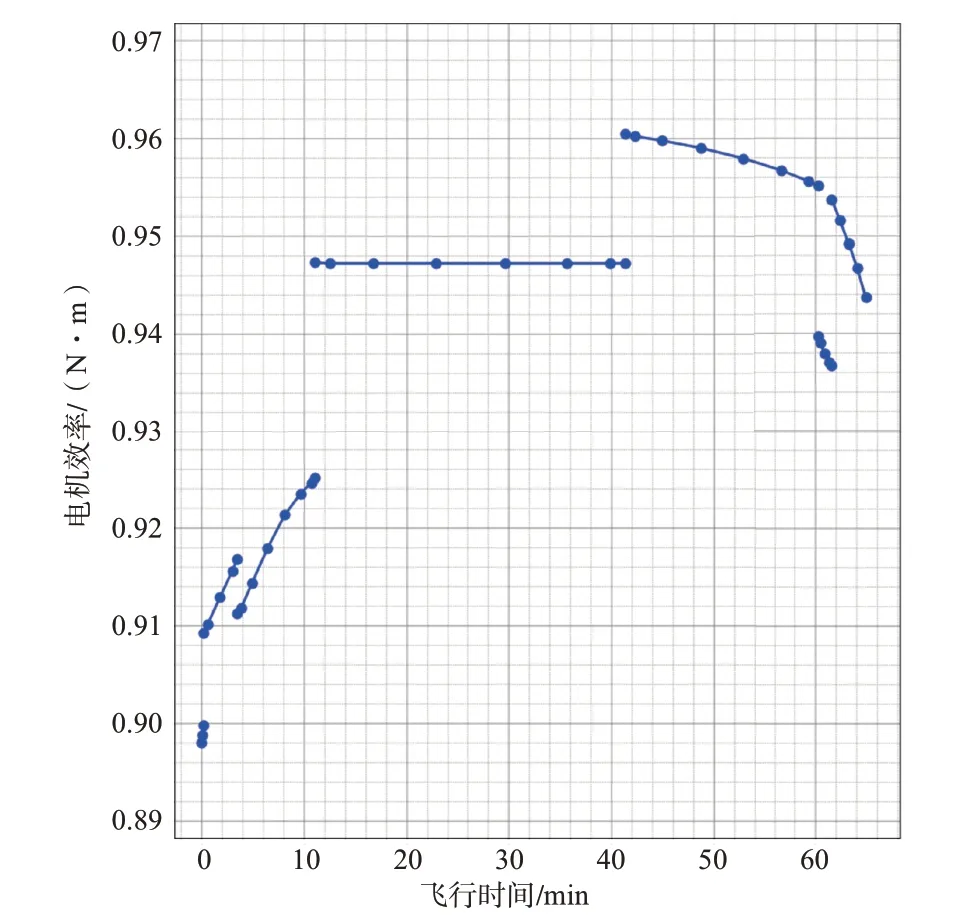
圖18 電機效率曲線Fig.18 Motor efficiency

圖19為電池的荷電狀態（SOC）的變化曲線，電池的荷電狀態是指電池中剩余電荷的可用狀態。圖20 為電池總能量的變化曲線，可以看出隨著飛行時間的增加，電池的SOC值和總能量在逐漸降低。

圖19 電池SOC變化曲線Fig.19 Curve of battery SOC change

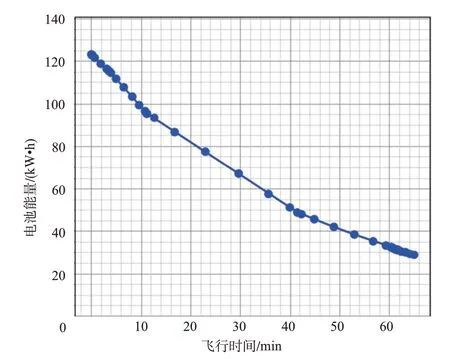
圖20 電池總能量變化曲線Fig.20 Curve of battery total energy

圖21 為電池的輸出功率曲線，可以發現，輸出功率高的階段，所對應的圖20 中能量變化曲線的斜率會相對較高。巡航條件下，輸出功率大概在95kW左右。

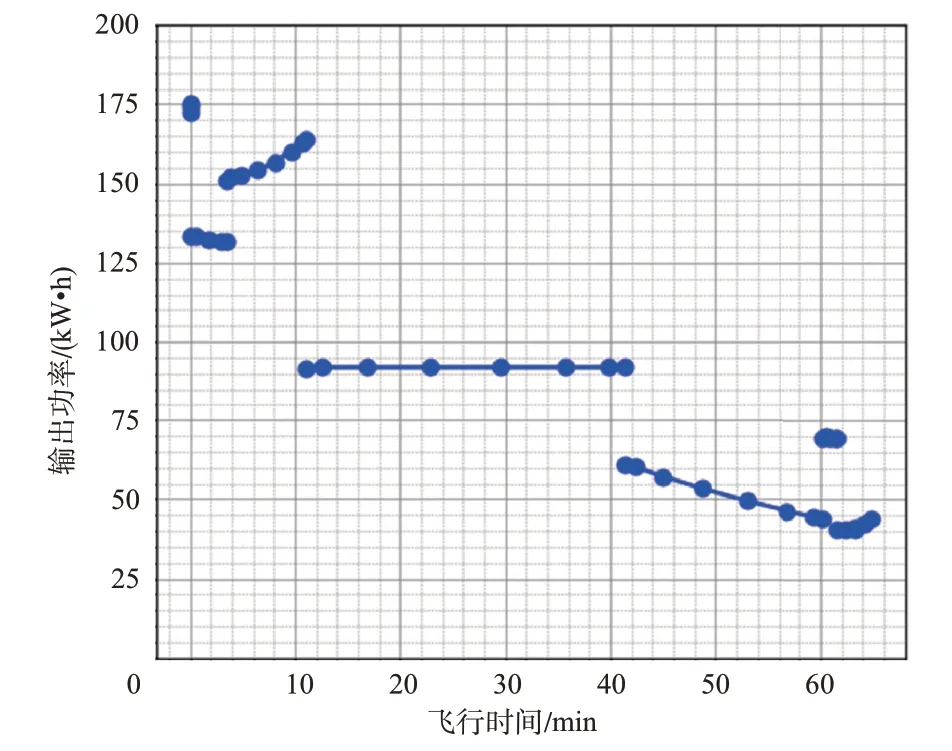
圖21 電池的輸出功率曲線Fig.21 Curve of battery output power

圖22為電池的電壓變化情況，圖中紅色曲線為開路的電壓變化情況，作為電池性能分析的參考值，而藍色曲線為帶負載的電壓變化，模擬真實負載的電池變化情況。由圖22可以得出，在飛機最后著陸時，電池的電壓會從一開始充滿狀態的500V 降至約454V，這些總體的電氣性能參數將為后續的電推進系統的詳細設計和優化提供參考。

圖22 電池的電壓變化曲線Fig.22 Curve of battery voltage

圖23為電池的放電倍率變化曲線，圖中紅色曲線表示標稱放電倍率變化情況，也是我們通常在選擇電池型號時主要的參考依據；藍色曲線表示瞬時放電倍率變化情況，由于電池的放電能力實際是隨著SOC值的降低而降低的，瞬時放電倍率可以作為瞬時放電能力的一種衡量標準，用于確定預留的安全電量，以提高整個系統的安全性。

圖23 電池放電倍率曲線Fig.23 Curve of battery C-Rate

4 結論

為了提高電動飛機在早期設計的效率，本文提出了一種分布式電推進飛機的多學科參數快速估計方法。通過研究，得出了以下結論：

（1）該方法對分布式電推進飛機進行總體框架搭建并初步建立了電推進系統模型，包括電池的放電模型、簡單電機模型以及螺旋槳模型。

（2）基于勢流理論，建立簡化氣動分析方法對螺旋槳與機翼的氣動—推進耦合特性進行分析，并與風洞試驗數據對比，驗證了該方法的準確性。

（3）建立飛機的典型飛行剖面，并利用該方法對某分布式電推進飛機進行多學科參數快速估計，得到了整個飛行剖面下的飛機氣動性能變化及能源系統的性能變化，驗證了該方法的實用性。

由該方法可以快速地得出分布式電推進飛機的性能參數，并為下一步開展更精細的分布式電推進飛機供配電架構研究及優化設計奠定了研究基礎。