包含串補的并網直驅風電場振蕩穩定性及可行域分析

季一寧 王海風,2

包含串補的并網直驅風電場振蕩穩定性及可行域分析

季一寧1王海風1,2

（1. 新能源電力系統全國重點實驗室（華北電力大學） 北京 102206 2. 四川大學電氣工程學院 成都 610064）

串補裝置廣泛存在于電力系統中，含串補的大規模直驅永磁同步發電機（PMSG）構成的風電場并網系統存在次同步振蕩范疇的小干擾失穩風險。針對上述現象，該文首先構建包含PMSG網側換流器控制模型、鎖相環控制模型以及含有串補裝置的線路動態模型的并網系統全階模型及等效模型。然后在不同的時間尺度下對等效模型進行化簡，運用勞斯-赫爾維茨判據求得各時間尺度場景下并網系統的穩定性判據，從機理上解釋了并網系統中各運行參數和控制參數之間的聯系及其對系統穩定性的影響。進一步通過一個包含15臺PMSG風電機組的并網風電場驗證了該文推導的穩定判據的正確性。最后基于可行域的分析，直觀地討論了串補線路和其他參數對系統穩定性的影響。

永磁直驅風機 串補 小干擾穩定性 穩定判據 可行域

0 引言

近年來，電力電子設備在電力系統中的占比日益增高，現代電力系統中傳統的機電設備被電力電子設備替換已經成為發展趨勢[1]。其中風電、光伏等新能源發電技術快速發展，截至2022年底，全國累計發電裝機容量約25.6億kW，其中并網的風電裝機容量約為3.7億kW，占總裝機容量的14.45%[2]，隨著大規模風電機組的入網，近年來國內外頻發頻率覆蓋面極廣的振蕩事故。其中，風電場并網系統引起的電力系統振蕩事故，嚴重影響了相關區域電網的安全穩定運行[3-8]。

在穩定性分析領域，對于包含串補的風電場并網系統的研究，現有文獻大多針對雙饋風電場[9-11]，對于直驅永磁同步發電機（direct Permanent Magnet Synchronous Generator, PMSG）通過串補線路并入交流電網的研究較少。文獻[12]通過對參與因子的計算表明，PMSG和串補線路的動態交互屬于RLC電氣諧振范疇，且系統次同步振蕩的主導模式取決于串補。文獻[13]的結果表明，PMSG的網側換流器控制參數、鎖相環（Phase Locked Loop, PLL）參數以及串補線路的參數都是并網系統次同步振蕩穩定性的關鍵影響因素。文獻[14]采用廣義奈奎斯特穩定判據分析了系統次同步振蕩的穩定性，其結果表明PMSG輸出的有功功率增加和串補度的增大均會給系統穩定帶來不利影響。文獻[15]描述了一個混合風電場模型，其中通過對振蕩模式的分析得出PMSG在并網系統中出力的占比越大，系統的穩定性越強，且當系統中串補度越大，振蕩模式的阻尼就越小，系統穩定性越弱。然而上述的研究更側重于仿真結果，難以適應未來運行工況的改變。為揭示含串補的PMSG風電場并網系統的穩定性變化規律，需要一種更加解析且直觀的方法。

風電場并網系統穩定性分析方法一般有如下兩種：阻抗分析法和模式分析法。其中文獻[16]將阻抗分析法和模式分析法相結合，研究了新疆哈密地區風電場次同步振蕩的機理，結果表明在弱連接條件下，并網系統中產生的等效負電阻是失穩的主要原因。文獻[17]分析了電壓控制、電流內環控制、鎖相環（PLL）控制、延時以及濾波器等環節共同作用疊加后的直驅風電場各頻段內阻抗特性的影響，從容性負電阻的角度解釋了PMSG并網系統的振蕩機理。文獻[18]通過模式分析法以及所提出的開環模式諧振理論，分析了雙饋風電場中各控制參數和串補之間的交互對系統穩定性的影響。然而運用阻抗分析法得出的系統阻抗為正是系統穩定的充分而非必要條件，這導致阻抗分析法的使用有其局限性。同時對于模式分析法，它可以給出研究對象的所有振蕩模式，是包含信息最全面的一種方法。但在使用模式分析法的時候，需要建立電力系統的電磁暫態級精細化模型，當以大規模風電場接入的電力系統作為研究對象時，其包含了成百上千臺風電機組，面對龐大的數學模型，通過模式計算法判斷電力系統振蕩模式的穩定性會面臨矩陣維數過大，消耗大量計算資源導致計算困難的問題。

并網系統的動態由換流器控制和線路動態共同構成，其動態特性是高階且復雜的。為了從解析的角度揭示包含串補線路風電場并網系統的振蕩穩定性規律，需要對該系統進行降階。本文按時間尺度對并網系統可能發生的振蕩進行分類。由文獻[19]可知，并網PMSG風電機組的網側換流器（Grid-Side Converter, GSC）的內、外環控制分別處于兩個不同的振蕩時間尺度中，其中頻率較高的時間尺度定義為交流電流時間尺度，其振蕩頻率為幾十赫茲；頻率較低的時間尺度定義為直流電壓時間尺度，其振蕩頻率為10 Hz以內。當分別考慮不同的時間尺度時，可以忽略非重點關注的時間尺度上的動態，這降低了并網系統動態特性的階數，以及求取解析穩定判據的難度。文獻[20]指出PLL的帶寬可以處于一個較寬的范圍，文獻[21-22]研究表明當鎖相環的振蕩頻率較高時，其處于交流時間尺度下，此時PLL和電流控制內環產生動態交互，系統容易引發振蕩失穩風險。同樣地，鎖相環振蕩頻率處于直流電壓時間尺度下時，也會和電壓外環發生交互作用。然而文獻[23]指出，較高的PLL帶寬不利于系統保持穩定，因此為了讓PLL對系統的影響更加明顯，本文僅考慮PLL自身的振蕩頻率處于交流電流時間尺度下的情況。

針對上述文獻的研究及其存在的問題，對于包含串補線路的PMSG并網直驅風電場進行穩定性分析，提出了一種基于不同時間尺度的模型簡化方法及相應的穩定判據。首先，建立用于小干擾分析的全階模型及風電場的降階模型；其次，根據所研究的不同的時間尺度，對并網系統中各部分進行合理的簡化，并求解簡化后模型的特征方程；再次，運用勞斯-赫爾維茨判據推導得到不同時間尺度下解析的穩定判據，給出系統在不同尺度下穩定性的機理解釋；最后，運用可行域的分析方法，可視化上述穩定判據的邊界，結合非線性仿真，驗證了本文推導的穩定判據的準確性。

1 含串補直驅風電機組并網電力系統模型

單臺PMSG與含串補線路的外部系統的連接示意圖如圖1所示。PMSG通過線路等效電抗L串補裝置等效電抗c及對地電容等效電抗cf與交流系統進行連接。其中c為網側換流器出口電壓；代表公共連接點（Point of Common Coupling, PCC）電壓；b為等效交流系統的基準電壓；dc和dc分別為直流電容和直流母線電壓；f為網側換流器出口處的濾波電抗；m和分別為從機側換流器（Motor-Side Converter, MSC）流出的有功功率和流入網側換流器的有功功率；為從PMSG經過f流入PCC的電流；1為流入交流系統的電流。和1方向均以從PMSG到交流系統為正。

圖1 PMSG風電機組并網模型

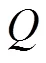
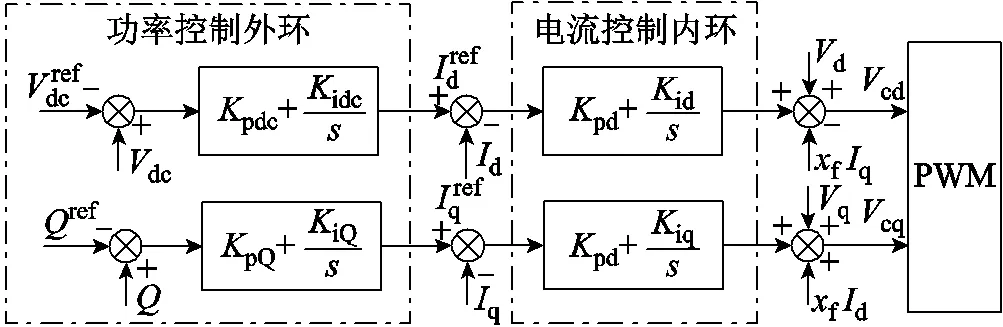
圖2 網側換流器矢量控制策略

根據圖2，功率控制外環的動態方程為

式中，v和Q分別為PMSG的d軸直流電壓控制外環和q軸無功功率控制外環的狀態變量；idc和iQ分別為直流電壓控制外環和無功功率控制外環的積分參數。

電流控制內環的動態方程為

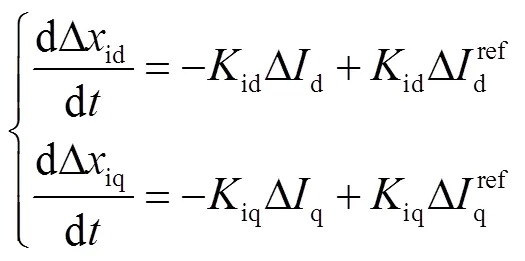
列寫PCC處的有功功率和無功功率方程，并線性化得到

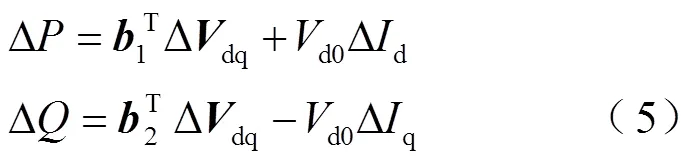
其中

換流器的脈寬調制一般采用平均值模型，則電流控制內環的輸出方程為

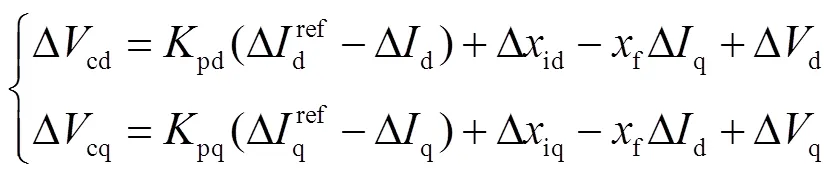
式中，pd和pq分別為電流控制內環d軸和q軸分量的比例參數。

圖3 鎖相環PLL線性化模型

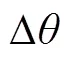
式中，p為鎖相環PLL的狀態變量。

同時，對于PCC處的電壓相位，線性化后有

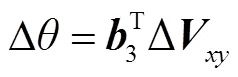
其中

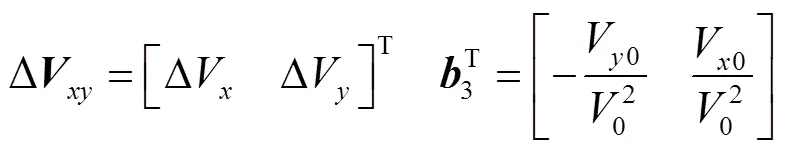
圖4 dq靜止坐標系和xy同步旋轉坐標系的關系示意圖

由圖4可以得到用于兩個坐標系之間轉換的等式為

其中

本文中PMSG和交流部分的連接方式如圖1所示，線路的參數包含電抗L，串補裝置的等效電抗c以及對地電容的等效電抗cf。線路的動態方程經線性化處理后得到

式中，1d和1q分別為流過串補裝置的d軸和q軸電流分量；Vcd和Vcq分別為等效對地電容兩端的d軸和q軸電壓分量。

自此完成了含串補直驅風電機組并網電力系統模型中各部分的數學模型的建立，其中包括直流電容dc模型、網側換流器GSC控制環節模型、GSC出口側濾波電抗f模型和鎖相環PLL模型，不同坐標系下物理量轉換模型以及包含串補的線路模型。聯立式（1）～式（10），得到包含線路動態的并網PMSG的15階線性化模型為

對于如圖5所示的由臺PMSG機組構成的風電場并網系統，其中Lw為風電場并網系統線路的等效電抗，cw為風電場并網系統串補裝置的等效電抗。根據文獻[24]可以得到如下結論，當各臺PMSG同一型號且初始參數設定相同，即并網系統中各風電機組處于同構狀態且與外部電力系統通過長線路連接時，該并網風電場可等效為個等效子系統，其中前-1臺可以被認為有良好的穩定性，風電場與外部電力系統間交互的穩定性僅體現在第個等效子系統中。

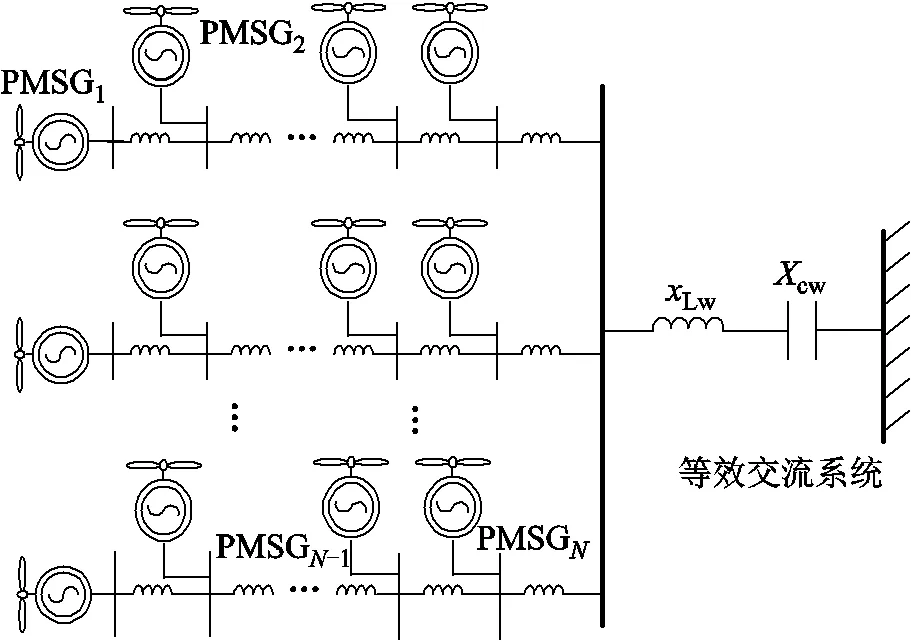
圖5 并網風電場結構

此時風電場由一臺等值PMSG和對應的等值電抗動態等效。對于圖5，等效電抗L=Lw和c=cw。

2 簡化模型及其穩定性判據

為了從解析的角度揭示式（11）所對應模型的振蕩穩定性規律，需要對模型中相關環節進行合理省略，本文按時間尺度對并網系統可能發生的振蕩進行分類。當研究交流電流時間尺度時，PLL動態、串補線路動態及電流內環控制可能存在交互作用，引發并網系統失穩；當研究直流電壓時間尺度時，電流內環控制的動態可以被忽略，本文僅考慮PLL處于較高頻帶的情況，此時處于交流電流時間尺度的PLL動態也將被忽略，當電壓外環參數設置不合理時，并網系統也會有失穩的風險。下面將詳細討論這兩種時間尺度下系統的簡化模型以及穩定判據的推導。

2.1 交流電流時間尺度下并網系統穩定性分析

當研究并網系統在交流電流時間尺度下的振蕩穩定性，忽略速度較慢的功率控制外環時，存在

聯立式（2）、式（4）、式（6）和式（12），得電流控制內環的線性化模型為

從式（13）可知，此時電流內環和濾波電抗f的動態特性與外部輸入量無關，僅受自身狀態變量影響。這意味著當忽略功率控制外環時，電流控制內環與鎖相環PLL的穩定特性相互獨立，此時若鎖相環PLL的動態特性位于交流電流時間尺度下，也不會和電流內環產生交互影響。

其中

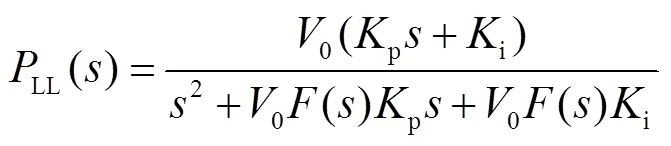
對于線路部分，因本文重點關注次同步及以下頻率振蕩范疇的小干擾失穩風險，而線路的對地電容的振蕩頻率為kHz級，故可以忽略該對地電容對系統振蕩穩定性的影響。進一步，本文中包含串補的線路為式（15）的線性化模型。

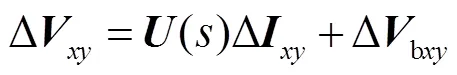
其中

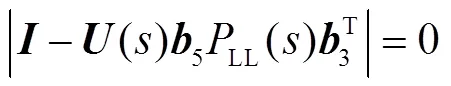
分析式（16），可列寫出特征方程，即

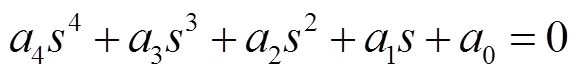
其中

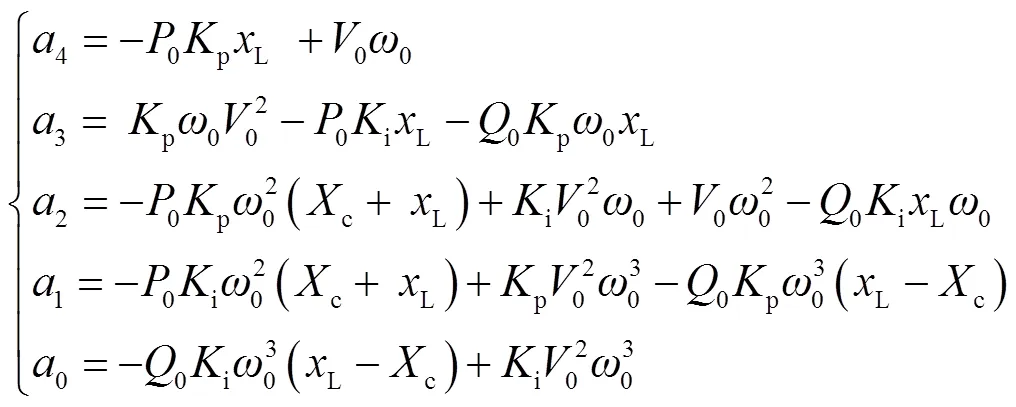
根據勞斯-赫爾維茨判據，該四階多項式對應系統穩定的充分必要條件為

其中

進一步簡化式（18）的第一式，可得

式（18）的第二式將被簡化為

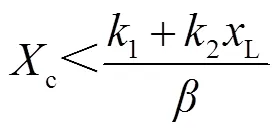
通過式（20）可知，當考慮串補線路后的動態特性，線路電抗L固定不變時，系統的穩定性反而隨著線路串補度的增大而降低，當線路串補度大于臨界值時，系統將失去穩定性。通常情況下，1+2L取值為負，這意味著選擇合適的串補裝置的等效電抗c，可使并網系統穩定。式（20）是含有線路電抗L的線性多項式，這意味著線路電抗L的大小將影響串補裝置的等效電抗c的穩定取值區間。此外，由式（18）可知，并網系統的穩定性同時受到鎖相環PLL控制參數的取值，以及PMSG風電機組的出力的影響。

2.2 直流電壓時間尺度下并網系統穩定性分析

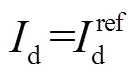
其中

式中，pdc和pQ分別為直流電壓控制外環和無功功率控制外環的比例參數。

將式（5）代入式（21）可得

聯立式（8）、式（9）和式（22）可得

其中

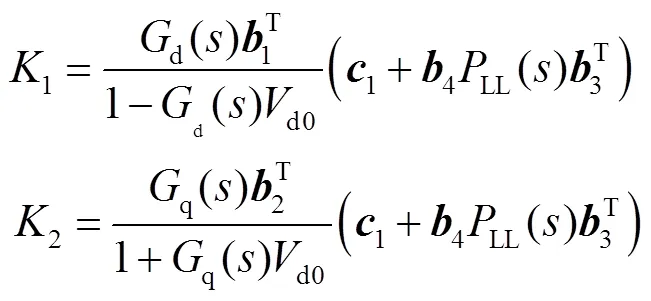
由文獻[10]可知，與線路相關的次同步振蕩模式會隨著串補度的增大而降低，其頻率區間從幾十赫茲到十幾赫茲單調遞減。當串補度處于較低的水平時，與線路相關的次同步振蕩模式的頻率較高。所以，在進行直流電壓時間尺度并網穩定性研究時，可以忽略含串補的線路的動態特性，即滿足()=(0)，代入式（15）中可以得到

本文考慮PLL的振蕩頻率處于交流電流時間尺度，鎖相環PLL的動態特性可不考慮，即LL()=1。簡化式（23）并聯立式（24），可得式（25）的特征方程，該模型的穩定性由該特征方程決定。

其中

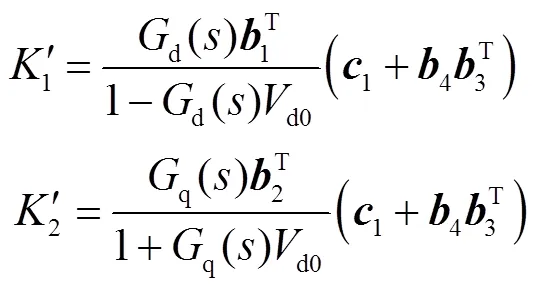
分析式（25），可以列寫出特征方程為

其中

根據勞斯-赫爾維茨判據,當且僅當滿足式（27）時，該三階多項式對應的系統處于穩定。

其中

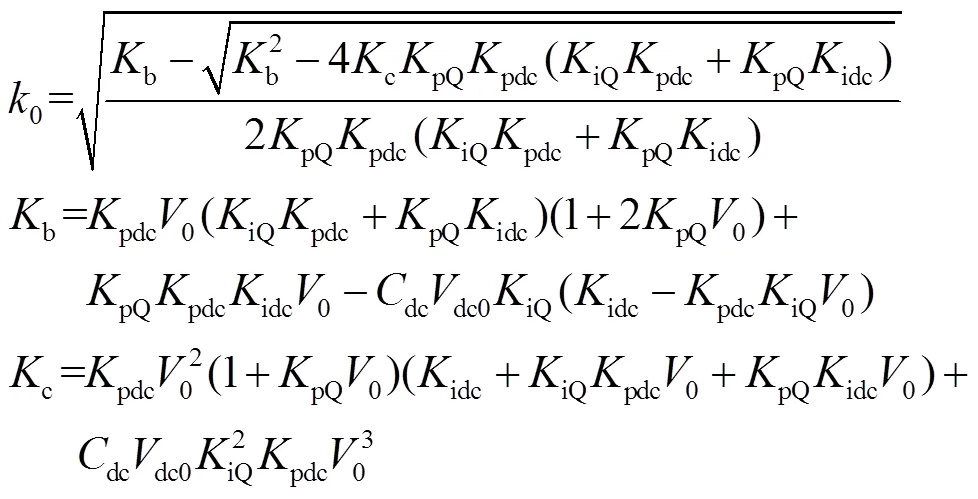
分析式（27）可知，當鎖相環PLL的控制參數運行在交流電流時間尺度時，該并網系統在直流電壓時間尺度依舊會發生系統不穩定的情況。當負荷過重，即0過大時，或者當系統連接較弱，即線路的等效電抗L-c較大時，都將導致系統阻尼減弱。同時，由式（27）可以看出，串補的加入將有利于系統的穩定性，串補度越大其等效電抗L-c越小，系統的連接性越強。式（27）從原理上解釋了在不考慮線路動態特性的情況下，弱電網以及重負荷對系統穩定性存在不利的影響。同時，也能夠解釋當發生直流電壓時間尺度下的振蕩且網側換流器外環參數設置不合理時，影響系統振蕩穩定性。

3 算例分析

本文以圖6所示系統進行算例分析，該算例模型為一個15臺PMSG組成的并網風電場，每臺PMSG采用文獻[25]給出的15階模型及運行工況，該風電場的所有PMSG風電機組由同一廠家生產，故其擁有相同的物理參數。此外，假設風電場的風為勻速，因此該風電場中所有PMSG風電機組的負載條件相同。同時，為每臺PMSG風電機組設置相同的控制策略。該算例中，由于風電場離等效交流系統較遠，通過一條帶串補的長線路與等效交流系統連接。根據第1節中的結論，算例所示系統的小干擾穩定性等效于圖1所示系統的小干擾穩定性，其中僅有的區別為L=15Lw和c=15cw。

圖6 15臺PMSG組成的并網風電場算例系統

3.1 交流電流時間尺度下的穩定性分析

基于上述算例，調節鎖相環參數（p=90，i= 15 000）使其處于一個較高的頻率范圍，同時考慮串補線路的動態特性，由式（11）表示的全階系統的部分模式如圖7所示。由圖7可知，隨著串補裝置等效電抗c值從0增加到0.8(pu)，主導模式逐漸靠近虛軸，系統穩定性減弱。當c＜0.59(pu)時，所有特征根都保持在左半平面，表明系統能夠穩定運行；當c＞0.59(pu)時，主導模式自左向右穿越了虛軸，從而導致系統發散失去穩定。該主導模式的振蕩頻率在38 Hz附近，通過參與因子的分析，該主導模式為鎖相環PLL模式。以上結果說明，串補裝置等效電抗c的增大將導致鎖相環PLL模式失穩。

圖7 串聯補償裝置等效電抗Xc變化時根軌跡

當c和L改變時，三種不同工況下由模式分析得出的全階并網系統的閉環特征根、等效系統的閉環特征根以及穩定判據得出的結果見表1，驗證了等效系統及穩定判據的正確性。

表1c和L變化時判據結果及各系統特征根

Tab.1 Criterion results and eigenvalues of each system when Xc and xL varied

進一步分析并網系統穩定時串補裝置等效電抗c的取值范圍，在工況參數下逐漸增大線路的等效電抗L，結果如圖8所示。

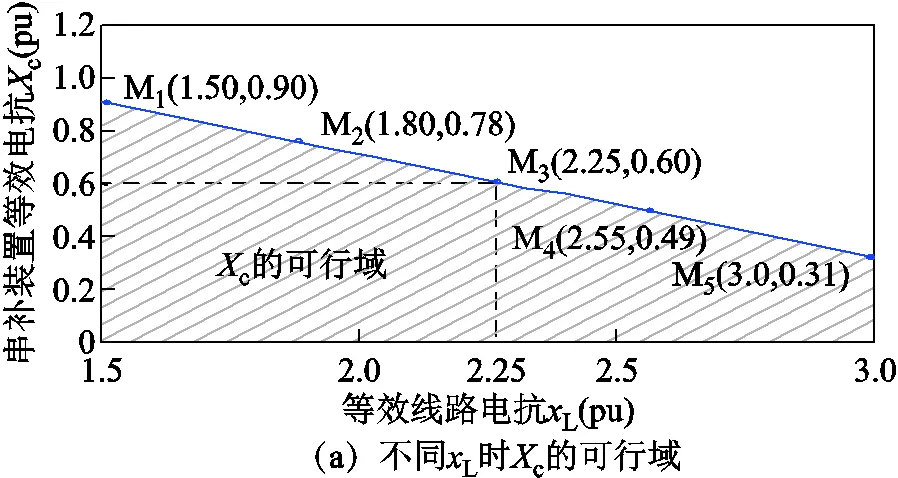
圖8 不同線路電抗xL下系統穩定的Xc可行域及非線性仿真結果

圖8a中藍色線左下方陰影區和坐標軸圍成的區域即為系統穩定時串補裝置等效電抗c的可行域。隨著線路等效電抗L的增大，系統抗擾動能力降低，表現為當L增大時，串補裝置的可行域范圍縮小，即系統的連接性越弱，系統可容納的串補裝置就越小。對等效后的系統進行非線性仿真，使PMSG的有功出力在0.1 s時增加至原來的1.05倍，在0.2 s時恢復至原來的有功功率。如無明確說明，后續算例的非線性仿真均采用該擾動方式，下文不再贅述。表1中三種工況對應的非線性仿真結果如圖8b所示，表明所推導的判據是正確的。

進一步研究PMSG有功功率變化對并網穩定性及對c取值范圍的影響。同樣地，表2給出了三種不同工況下全階和等效系統的閉環特征根和穩定判據結果。

表20和c變化時判據結果及各系統特征根

Tab.2 Criterion result and eigenvalues of each system when P0 and Xc varied

在其他參數不變的情況下，逐漸增加等效PMSG風電機組的出力，系統穩定的c可行域及不同工況下非線性仿真結果如圖9所示。

圖9a中陰影區域即為系統穩定時串補裝置等效電抗c的可行域。由該可行域可知，當PMSG出力不變時，系統的穩定性隨著c的增加而減弱。另一方面，隨著PMSG出力0增大，c可行域范圍縮小，表明當系統的負載過大時，系統抗擾動能力減弱，系統的穩定性越差。圖9b為表2中三種工況在等效系統中的非線性仿真結果，其結論一致表明穩定判據的正確性。

圖9 不同PMSG有功功率下系統穩定的Xc可行域及非線性仿真結果

為研究鎖相環參數的變化對c取值范圍的影響，表3給出了三種不同工況時全階和等效系統的閉環特征根和對應的判據結果。

表3p和c變化時判據結果及各系統特征根

Tab.3 Criterion result and eigenvalues of each system when Kp and Xc varied

進一步地，在其他參數不變的情況下，逐漸增加鎖相環PLL的p參數，其可行域如圖10a陰影區域所示。

圖10 不同Kp時系統穩定的Xc可行域及非線性仿真結果

由該可行域可知，當鎖相環p取值不變時，隨著c的增加，系統的穩定性將下降。同時，隨著鎖相環p取值增大，串補裝置的可行域范圍擴大，表明系統抗擾動能力增強，即系統的穩定性隨著p的增大而增強。圖10b為三種工況時的非線性仿真，其結果和圖10a所示的可行域以及表3的結論吻合。

3.2 直流電壓時間尺度下的穩定性分析

在本節中，仍保持鎖相環處于一個較高的振蕩頻率，當研究處于直流電壓時間尺度的振蕩穩定性時，圖11為式（11）對應的全階模型在串聯補償裝置等效電抗c變化時的根軌跡。當c＜0.24(pu)時，有一個特征根處于右半平面，此時系統失穩；當c＞0.24(pu)時，該特征根自右向左穿越了虛軸，此時所有特征根都處于虛軸左側，因此系統穩定。該主導模式的振蕩頻率在2 Hz附近，分析參與因子可知，該主導模式與網側換流器外環控制參數及直流側電容相關，即隨著串聯補償裝置等效電抗c增大，外環控制參數及直流側電容造成的系統失穩將消失，印證了文獻[10]中隨著串補度變大系統將變得更加穩定。

圖11 串聯補償裝置等效電抗Xc變化時根軌跡

將該工況所對應參數應用于式（27）所示的穩定判據，得到當c＜0.22(pu)時系統穩定的結論，由此可見，本文所推導的穩定判據是準確且可靠的。

表4提供了當c和L改變時三種不同工況下由模式分析得出的全階并網系統的閉環特征根、等效系統的閉環特征根以及穩定判據得出的結果，驗證了穩定判據的正確性。

表4L和c變化時判據結果及各系統特征根

Tab.4 Criterion result and eigenvalues of each system when xL and Xc varied

進一步分析系統的穩定性和c參數的適用范圍，在其他參數不變的情況下，逐漸增大線路的等效電抗L，分析串聯補償裝置的等效電抗c使并網系統穩定的數值選區范圍，結果如圖12所示。

圖12 不同等效線路電抗xL下系統穩定的Xc可行域及非線性仿真結果

圖12a中陰影區域即為系統穩定時串補裝置等效電抗c的可行域，由該可行域可知，隨著線路等效電抗L的增大，系統抗擾動能力降低，這表現在當L增大時需要更大的串補裝置c才能使系統處于穩定。將系統中PMSG的有功出力在0.1 s時增加至原來的1.05倍，且在10 ms后恢復原始出力，如無明確說明，后續非線性仿真均采用該小擾動，不再贅述。圖12b為表4的三種工況下的非線性仿真結果。仿真結果和圖12a所示的可行域結論吻合，驗證了式（27）所推導穩定判據的準確性。

進一步研究PMSG出力變化對低振蕩頻率時并網穩定性以及對c取值范圍的影響。表5給出了三種不同工況下全階和等效系統的閉環特征根和判據結果。

表50和c變化時判據結果及各系統特征根

Tab.5 Criterion result and eigenvalues of each system when P0 and Xc varied

同樣在其他參數不變的情況下，逐漸增加等效PMSG風電機組的出力，可繪制可行域如圖13a所示。

圖13 PMSG不同有功功率下系統穩定的Xc可行域及非線性仿真結果

圖13a中藍色線左上方陰影區和坐標軸圍成的區域即為系統穩定時串補裝置等效電抗c的可行域。由該可行域可知，當PMSG出力不變時，隨著c的減小，將降低系統的穩定性。另一方面，隨著PMSG出力0增大，串補等效電抗c的可行域范圍縮小，表明系統抗擾動能力減弱，即系統的負載越大，系統的穩定性越差，需要更大的串補等效電抗c才能使系統穩定。圖13b為系統分別處在工況A、B和C時的非線性仿真圖，其結果符合可行域的結論，驗證了穩定判據的準確性。

為了研究網側換流器參數的變化對c取值范圍的影響以及對并網系統的穩定性影響。表6給出了三種不同工況下全階和等效系統的閉環特征根和判據結果。

表6pdc和c變化時判據結果及各系統特征根

Tab.6 Criterion result and eigenvalues of each system when Kpdc and Xc varied

進一步在其他參數不變的情況下，逐漸增加網側換流器外環pdc參數，繪制的可行域如圖14a所示。

圖14 網側換流器外環不同Kpdc時系統穩定的Xc可行域及非線性仿真結果

圖14a中陰影區域即為系統穩定時串補裝置等效電抗c的可行域。由該可行域可知，當鎖相環pdc取值不變時，隨著c的減小，系統的穩定性將降低。另一方面，隨著鎖相環pdc取值增大，串補裝置c取值的可行域范圍擴大，表明系統抗擾動能力增強，即系統的穩定性隨著p的增大而增強。圖14b為系統處在表6的三種工況時的非線性仿真結果，該結果和圖14a所示的可行域結論吻合，證明所推導的穩定判據的正確性。

4 結論

本文推導針對PMSG風電場通過含串補裝置的線路連接交流系統會產生振蕩失穩這一現象，分析了系統分別處于交流電流時間尺度和直流電壓時間尺度時振蕩的失穩機理，推導了適用于上述兩種情況的穩定判據，并在算例中繪制了并網系統的可行域。論文的主要研究結論如下：

本文推導的穩定判據從解析的角度直觀地揭示了系統穩定性與風電場運行參數及線路參數之間的聯系，并通過非線性仿真驗證了所提穩定判據的準確性。當并網系統處于直流電壓時間尺度下的振蕩時，系統的失穩風險將隨著串補裝置的等效電抗c的增加而減小；然而當系統處于交流電流時間尺度振蕩時，系統的失穩風險將隨著串補裝置的等效電抗c的增加而增加。本文對c的可行域進行分析，其結果表明，無論振蕩頻率處于何種時間尺度下，風電機組的出力增加均會增加風電場并網系統小干擾振蕩失穩的風險；當并網系統處于交流電流時間尺度下的振蕩時，等效電抗c的臨界穩定值隨著L的增大而減小，隨著鎖相環比例參數p的增大而增大；而當并網系統處于直流電壓時間尺度下的振蕩時，等效電抗c的臨界穩定值隨著L的增大而增大，隨著pdc的增大而減小。故當分析的時間尺度側重點不同時，由串補線路所帶來的穩定性風險的具體情況也將不同，且不同參數對等效電抗c臨界穩定值的影響也不相同。

[1] 馬偉明. 關于電工學科前沿技術發展的若干思考[J]. 電工技術學報, 2021, 36(22): 4627-4636.

Ma Weiming. Thoughts on the development of frontier technology in electrical engineering[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4627-4636.

[3] 邵冰冰, 趙崢, 肖琪, 等. 多直驅風機經柔直并網系統相近次同步振蕩模式參與因子的弱魯棒性分析[J]. 電工技術學報, 2023, 38(3): 754-769.

Shao Bingbing, Zhao Zheng, Xiao Qi, et al. Weak robustness analysis of close subsynchronous oscillationmodes’ participation factors in multiple direct-drive wind turbines with the VSC-HVDC system[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 754-769.

[4] 韓應生, 孫海順, 秦世耀, 等. 電壓源型雙饋風電并網系統小擾動低頻穩定性分析[J]. 電工技術學報, 2023, 38(5): 1312-1324, 1374.

Han Yingsheng, Sun Haishun, Qin Shiyao, et al. Low-frequency stability analysis of voltage-sourced doubly-fed wind power grid-connected system under small disturbance[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1312-1324, 1374.

[5] 顏湘武, 常文斐, 崔森, 等. 基于線性自抗擾控制的靜止無功補償器抑制弱交流風電系統次同步振蕩策略[J]. 電工技術學報, 2022, 37(11): 2825-2836.

Yan Xiangwu, Chang Wenfei, Cui Sen, et al. Sub-synchronous oscillation suppression strategy of weak AC wind power system with static var compensator based on linear active disturbance rejection control[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2825-2836.

[6] 劉其輝, 洪晨威, 逄思敏, 等. 基于彈性系數的雙饋風電機組控制參數對次同步振蕩作用分析及調整方法[J]. 電工技術學報, 2022, 37(14): 3528-3541.

Liu Qihui, Hong Chenwei, Pang Simin, et al. Analysis and adjustment method of doubly-fed fan control parameters on subsynchronous oscillation based on impedance elastic sensitivity[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3528-3541.

[7] 劉其輝, 逄思敏, 吳林林, 等. 大規模風電匯集系統電壓不平衡機理、因素及影響規律[J]. 電工技術學報, 2022, 37(21): 5435-5450.

Liu Qihui, Pang Simin, Wu Linlin, et al. The mechanism, factors and influence rules of voltage imbalance in wind power integration areas[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5435-5450.

[8] 薛峰, 吳家龍, 崔曉丹, 等. 基于阻抗辨識的沽源地區風電并網系統次同步振蕩控制策略[J]. 電力系統自動化, 2023, 47(5): 200-207.

Xue Feng, Wu Jialong, Cui Xiaodan, et al. Sub-synchronous oscillation control strategy based on impedance identification for wind power grid-connected system in Guyuan area of China[J]. Automation of Electric Power Systems, 2023, 47(5): 200-207.

[9] Song Yipeng, Blaabjerg F. Overview of DFIG-based wind power system resonances under weak networks[J]. IEEE Transactions on Power Electronics, 2017, 32(6): 4370-4394.

[10] Liu Huakun, Xie Xiaorong, Zhang Chuanyu, et al. Quantitative SSR analysis of series-compensated DFIG-based wind farms using aggregated RLC circuit model[J]. IEEE Transactions on Power Systems, 2017, 32(1): 474-483.

[11] Xie Xiaorong, Zhang Xu, Liu Huakun, et al. Characteristic analysis of subsynchronous resonance in practical wind farms connected to series-compensated transmissions[J]. IEEE Transactions on Energy Conversion, 2017, 32(3): 1117-1126.

[12] Zhao Shuqiang, Wang Nan, Li Ren, et al. Sub-synchronous control interaction between direct-drive PMSG-based wind farms and compensated grids[J]. International Journal of Electrical Power & Energy Systems, 2019, 109(7): 609-617.

[13] Xu Yangkun, Zhang Miao, Fan Lingling, et al. Small-signal stability analysis of type-4 wind in series-compensated networks[J]. IEEE Transactions on Energy Conversion, 2020, 35(1): 529-538.

[14] Beza M, Bongiorno M. On the risk for subsynchronous control interaction in type 4 based wind farms[J]. IEEE Transactions on Sustainable Energy, 2019, 10(3): 1410-1418.

[15] 王俊茜, 賈祺, 劉侃, 等. 混合風電場接入含固定串補系統的次同步振蕩特性分析[J]. 可再生能源, 2022, 40(5): 651-659.

Wang Junxi, Jia Qi, Liu Kan, et al. Analysis of subsynchronous oscillation characteristics of hybrid-based wind farm connected with fixed series compensation system[J]. Renewable Energy Resources, 2022, 40(5): 651-659.

[16] Liu Huakun, Xie Xiaorong, He Jingbo, et al. Subsynchronous interaction between direct-drive PMSG based wind farms and weak AC networks[J]. IEEE Transactions on Power Systems, 2017, 32(6): 4708-4720.

[17] 李光輝, 王偉勝, 劉純, 等. 直驅風電場接入弱電網寬頻帶振蕩機理與抑制方法(一)：寬頻帶阻抗特性與振蕩機理分析[J]. 中國電機工程學報, 2019, 39(22): 6547-6562.

Li Guanghui, Wang Weisheng, Liu Chun, et al. Mechanism analysis and suppression method of wideband oscillation of PMSG wind farms connected to weak grid (part Ⅰ): analysis of wideband impedance characteristics and oscillation mechanism[J]. Proceedings of the CSEE, 2019, 39(22): 6547-6562.

[18] Du Wenjuan, Wang Yang, Wang H F. Strong sub-synchronous control interactions caused by open-loop modal resonance between the DFIG and series-compensated power system[J]. International Journal of Electrical Power & Energy Systems, 2018, 102: 52-59.

[19] 袁小明, 程時杰, 胡家兵. 電力電子化電力系統多尺度電壓功角動態穩定問題[J]. 中國電機工程學報, 2016, 36(19): 5145-5154, 5395.

Yuan Xiaoming, Cheng Shijie, Hu Jiabing. Multi-time scale voltage and power angle dynamics in power electronics dominated large power systems[J]. Proceedings of the CSEE, 2016, 36(19): 5145-5154, 5395.

[20] Li Yin, Fan Lingling, Miao Zhixin. Wind in weak grids: low-frequency oscillations, subsynchronous oscillations, and torsional interactions[J]. IEEE Transactions on Power Systems, 2020, 35(1): 109-118.

[21] Zhao Mingquan, Yuan Xiaoming, Hu Jiabing, et al. Voltage dynamics of current control time-scale in a VSC-connected weak grid[J]. IEEE Transactions on Power Systems, 2016, 31(4): 2925-2937.

[22] 吳廣祿, 周孝信, 王姍姍, 等. 柔性直流輸電接入弱交流電網時鎖相環和電流內環交互作用機理解析研究[J]. 中國電機工程學報, 2018, 38(9): 2622-2633, 2830.

Wu Guanglu, Zhou Xiaoxin, Wang Shanshan, et al. Analytical research on the mechanism of the interaction between PLL and inner current loop when VSC-HVDC connected to weak grid[J]. Proceedings of the CSEE, 2018, 38(9): 2622-2633, 2830.

[23] 劉佳寧. 高比例風光并網系統穩定機理與功率振蕩分析[D]. 杭州: 浙江大學, 2022.

Liu Jianing. Stability mechanism and power oscillation analysis of power system with high-penetration wind power and photovoltaic generation[D]. Hangzhou: Zhejiang University, 2022.

[24] Du Wenjuan, Dong Wenkai, Wang Haifeng, et al. Dynamic aggregation of same wind turbine generators in parallel connection for studying oscillation stability of a wind farm[J]. IEEE Transactions on Power Systems, 2019, 34(6): 4694-4705.

[25] Du Wenjuan, Ren Bixing, Wang Haifeng, et al. Comparison of methods to examine sub-synchronous oscillations caused by grid-connected wind turbine generators[J]. IEEE Transactions on Power Systems, 2019, 34(6): 4931-4943.

Analysis of Oscillation Stability and Feasible Region of Parameters in Grid-Connected Direct-Drive Wind Farm with Series Compensation

Ji Yining1Wang Haifeng1,2

（1. State Key Laboratory of Alternate Electrical Power System with Renewable Energy Resources North China Electric Power University Beijing 102206 China 2. College of Electrical Engineering Sichuan University Chengdu 610064 China）

Series compensation devices are widely used in power systems. The wind farms grid-connected system composed of large-scale direct permanent magnet synchronous generator with series compensation has the risk of small interference instability in the sub-synchronous oscillation category. Most of the existing literatures are aimed at doubly-fed wind farms. There are few studies on the PMSGs grid-connected wind farm system through series compensation lines, and most of them are based on simulation analysis, lacking in-depth research on the mechanism and analysis of the relationship between various parameters. At the same time, the stability analysis methods of wind farm grid-connected system generally include impedance analysis and mode analysis. However, the system impedance obtained by impedance analysis method is a sufficient but not necessary condition for system stability, which leads to its limitations. Mode analysis method needs to establish a refined model of electromagnetic transient level of power system. When the model scale is too large, there are some problems such as difficult calculation and longtime consumption.

Aiming at the research of the above literatures and existing problems, this paper puts forward a simplified model method and corresponding stability criterion based on different time scales for the stability analysis of PMSG grid-connected wind farm with series compensation lines. Firstly, a full-order model of the system for small signal analysis is established, which can be used to clarify the dominant mode of the system. Then, according to the different time scales studied, each part of the grid-connected system is reasonably simplified and the simplified characteristic equation is solved. Then the analytical stability criteria at different time scales are obtained by using Routh-Hurwitz criterion, and the mechanism explanation of the stability of the system at different time scales is given. Finally, the boundary of the stability criterion is visualized by using the analysis method of feasible region, and the accuracy of the stability criterion is verified by nonlinear simulation.

According to the simulation results, when studying the oscillation on the time scale of AC current, the oscillation frequency of the dominant mode of the system is around 38 Hz, and this mode is a phase-locked loop mode, which is unstable with the increase of the equivalent reactancecof the series compensation device. Through the analysis of feasible region, the critical stable value ofcdecreases with the increase ofLand increases with the increase ofp. When studying the oscillation on the time scale of DC voltage, the oscillation frequency of the dominant mode of the system is around 2 Hz, and this mode is the outer loop mode of the grid-side converter, which is unstable with the decrease of the equivalent reactancec. Through the analysis of feasible region, the critical stable value ofcincreases with the increase ofLand decreases with the increase ofpdc.

In summary, this paper has the following conclusions: (1) According to the different frequency ranges, this paper simplifies the grid-connected system and lists the simplified characteristic equation. (2) When the grid-connected system oscillates in the time scale of DC voltage, the instability risk of the system decrease with the increase ofc. However, when the system oscillates in the time scale of AC current, the instability risk of the system increase with the increase ofc. (3) When the time scale of analysis is different, different parameters have different effects on the critical stability value ofc.

Direct-drive permanent magnet wind turbine, series compensation, small disturbance stability, stability criterion, feasible region

TM712

10.19595/j.cnki.1000-6753.tces.230628

國家自然科學基金資助項目（52077144）。

2023-05-05

2023-10-27

季一寧 男，1992年生，博士研究生，研究方向新能源電力系統穩定性分析與控制。E-mail：30299041@163.com（通信作者）

王海風 男，1960年生，教授，博士生導師，研究方向為電力系統穩定性分析與控制等。E-mail：hfwang60@qq.com

（編輯 赫 蕾）