基于貝葉斯隨機方法的高原湖泊水位模擬預測

韋彥玲，王 飛，陳 晶，高澤坤，高 凱，顧世祥，

(1.云南農業大學城鄉水安全與節水減排高校重點實驗室，云南 昆明 650201；2.云南秀川水利水電勘察設計有限公司，云南 昆明 650021；3.云南省水利水電勘測設計研究院，云南 昆明 650021)

天然湖泊水位的變化是流域降水、徑流、蒸發、氣溫、風速、水資源管理、湖泊管理等諸多自然-社會二元因素共同作用的結果[1]，存在非常復雜的非線性關系和不確定性。建立具有物理意義的數字孿生流域分布式水文模型是無限逼近湖泊水位變化真值的理想化途徑。但各類用水消耗等基礎資料條件、各個因子變量交互作用刻畫都影響到輸出結果質量。SVR和BP模型是常用的機器學習模型，可以較好地捕捉湖泊水位復雜的非線性關系[2-3]，但無法考慮時序變化[4-5]，且多為灰箱或黑箱模型，利用數據值實現，不干擾數據的統計分布和內部關系以及問題的物理性質，容易出現過擬合問題且多不能給出明確的解析表達式[6]。基于Copula的建模方法中，Vine Copula是一種統計動力學模型，可將高維的聯合分布分解為二元聯結的層次結構，能有效地描述高維變量之間的相依性，并在洪水特征、降雨徑流模擬、湖泊水位、干旱預測等成功應用[7-10]。在實際預測中，單一模型預測結果存在較大不確定性，不能充分捕捉數據特征[11]，且都有自身的優缺點。為克服單一模型的局限性，國內外學者構建了組合預測模型來整合單一模型發揮優勢[5，12-14]，但是確定性的組合模型無法定量評估模型結構的不確定性。

貝葉斯模型平均(BMA)是一種基于貝葉斯統計學的模型選擇方法，在提供精度更高的預測結果的同時，還能提供可靠的預測概率，定量評價模型結構不確定性對預測結果的影響[15-16]。BMA也被廣泛應用于水文學領域，如Wei等基于BMA算法整合不同數據源降水信息，結果表明BMA集成降水產品表現出更好的性能[17]。Yang等通過BMA方法在8個ET模型的基礎上對日ET估算改進，結果表明BMA方法優于個體ET模型[18]。俞明哲等利用BMA方法構建全球尺度洪水中長期預報模型，有效減小模型不確定性[19]。周婷等基于BMA方法對ELM、SVM、MARS3種模型的徑流預測結果組合，獲取可靠的中長期日徑流預測結果[20]。然而目前基于機器學習模型和統計動力學模型結合的BMA集成預測長時序湖泊水位的研究較少。本文針對流域各類用水消耗信息缺失條件下，引入貝葉斯隨機預測方法，對選擇氣象水文因素與前1月水位作為變量的Vine Copula、BP和SVR模型的預測結果構建了貝葉斯模型平均(BMA)對長時序湖泊水位進行集成預測，提高預測精度，并以杞麓湖為例檢驗，以期為湖泊水位調控、干旱預警管理、水生態保護治理等提供參考。

1 材料與方法

1.1 研究區域概況

杞麓湖是云貴高原上一個封閉型高原湖泊，是關系通海縣經濟和民生的“母親湖”，為當地周邊農業提供灌溉，具有調蓄、防洪、養殖和調節氣候等功能。杞麓湖盆區地處低緯高原，屬于亞熱帶半濕潤季風氣候，四季不分明，冬無嚴寒，夏無酷暑，四季如春，主要分干濕兩季。自20世紀80年代中后期以來，杞麓湖水質受污染的程度日趨嚴重[21]。2010年前后連續幾年的干旱造成杞麓湖天然補水減少、湖泊及流域地下水位較低，流域水生態安全面臨嚴重威脅，湖泊治理與保護形勢至今仍然十分嚴峻。

1.2 數據來源

①通海氣象站1964—2019年逐月降水、溫度、蒸發等觀測資料；②經過徑流還原分析得到的杞麓湖1964—2019年逐月入湖徑流量數據；③杞麓湖1964—2019年逐月實測水位。

1.3 研究方法

從水文循環的角度分析，水位變化主要受降水、溫度、蒸發、徑流以及前期水位的影響。將降水(P)、溫度(T)、蒸發(E)、徑流(F)、前一月水位(Zt-1)作為解釋變量，分別構建Vine Copula、BP、SVR模型進行長時序水位預測。Vine Copula、BP、SVR的3種模型預測值分別用V1-V3表示。

V1(t)=VC(Z(t-1)，P(t)，E(t)，F(t)，T(t))

(1)

V2(t)=BP(Z(t-1)，P(t)，E(t)，F(t)，T(t))

(2)

V3(t)=SVR(Z(t-1)，P(t)，E(t)，F(t)，T(t))

(3)

BMA方法是利用貝葉斯統計理論建立的概率預報模型，具體公式推導參見文獻[22-24]。它的基本原理如下：設目標月份的水位(即預測變量)為X1，給定觀測值Z=(Z1，Z2，…，Zt)，則BMA(VC，BP，SVR)模型的預測變量X1的概率密度函數表達式為

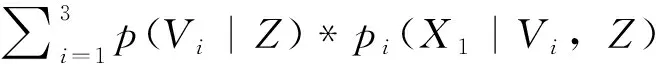
(4)

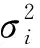
(5)

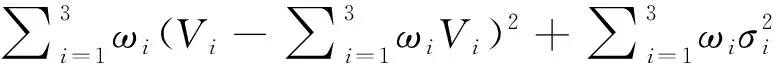
(6)

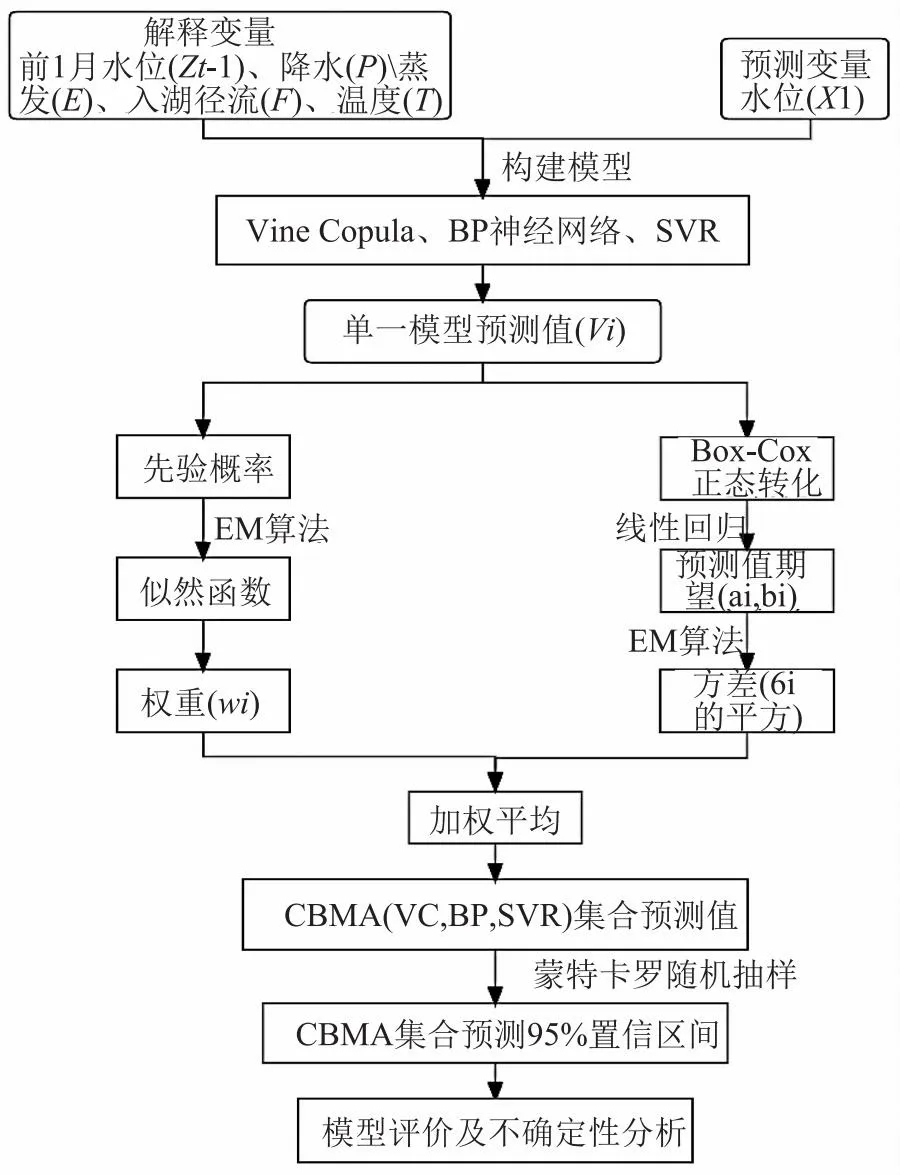
圖1 組合模型湖泊水位預測流程圖

為評估模型預測杞麓湖水位的效果，采用平均偏差(ME)、均方根誤差(RMSE)、符合指數(IA)、Nash-Sutcliffe效率系數(NSE)等4個常用的誤差統計指數。

2 結果與分析

2.1 模型預測結果分析

在模型構建中，將70%的數據樣本作為訓練集，30%的數據樣本作為驗證集。將單一模型和組合模型實測值與預測值對比并計算統計指數，如圖2所示。在單一模型中，Vine Copula模型預測精度最高，BP和SVR模型預測精度相差不大，但是SVR模型預測精度稍微高于BP模型。BMA(VC，BP，SVR)模型預測精度都高于單一模型Vine Copula、BP和SVR模型，其ME、RMSE、IA和NSE分別是0.05，0.15，0.991，0.962。BMA(VC，BP，SVR)模型得到的Vine Copula、BP和SVR模型權重分別為0.39、0.26、0.35，可看出模型預測精度越高，在BMA構建的模型中所占的權重也較高。

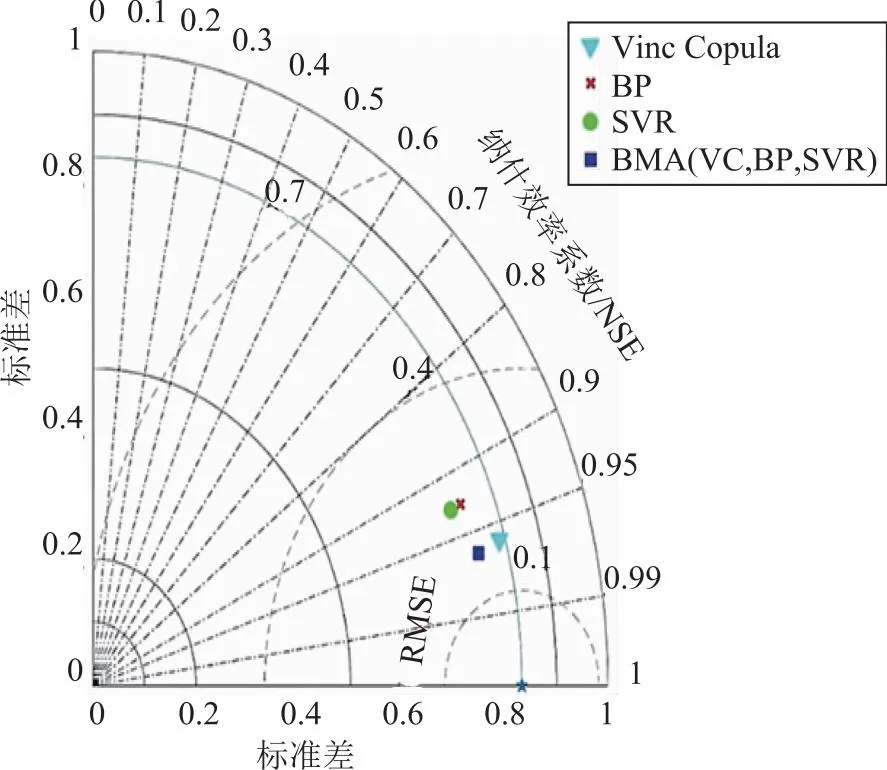
圖2 (VC，BP，SVR)不同模型對實測值的泰勒圖

將各模型預測水位和實測水位對比，如圖3所示。對水位的變化過程各模型均能較好描述，預測水位的趨勢基本與觀測水位一致，BP(R=0.97)和SVR(R=0.97)模型的水位預測值與實測值偏離較大，Vine Copula模型和BMA(VC，BP，SVR)模型預測序列與觀測序列基本重疊，但是在一些出現峰值的情況預測結果不理想，與觀測序列有些偏差。在一些個別年份BMA(VC，BP，SVR)模型預測誤差大于單個模型，主要體現在BP和SVR模型的水位預測值與實測值偏離較大的月份，這可能是因為BMA的權重值是由3種模型訓練集數據獲得的，權重的不穩定性會導致測試集個別月份預測效果減弱，同時在3種預測模型中預測效果較差的月份占比較多，會降低組合預測精度，甚至低于單一模型中預測精度最好的模型。在整體預測中，BMA(VC，BP，SVR)(R=0.99)模型預測精度高于Vine Copula(R=0.98)。

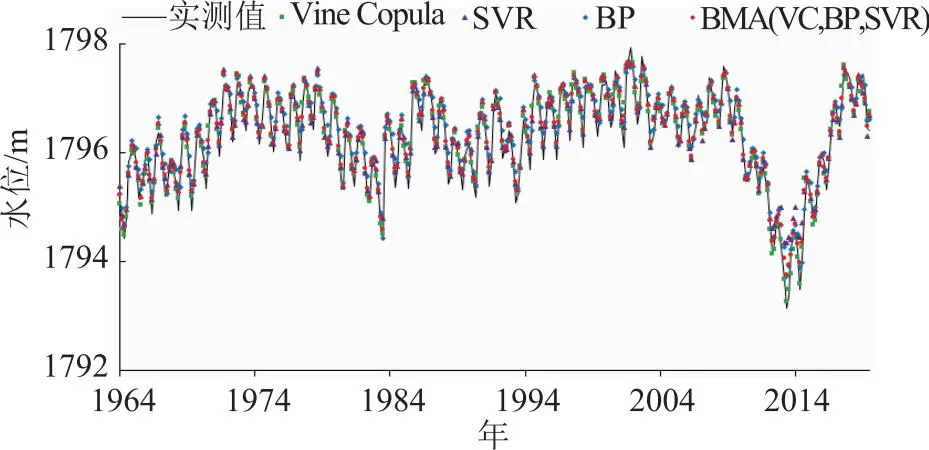
圖3 (VC，BP，SVR)不同模型逐月水位預測值與實測值時間序列對比圖

VC，BP，SVR，BMA等不同模型預測誤差統計見表1，在單個模型中BP模型相對誤差小于15%、20%、25%的占比最多，SVR模型在相對誤差小于25%的占比高于Vine Copula模型，這表明BP和SVR模型對時間序列的局部特征捕捉能力更強，可以避免重要特征丟失；而Vine Copula模型在相對誤差5%和10%的占較多，可以較好捕捉時間序列的時序特征，在整體上和極值的預測結果更加準確。BMA(VC，BP，SVR)模型可以整合單一模型預測優勢，使相對誤差小于15%的占比得到提升，提取更多數據特征，提高預測精度。

表1 不同方法模型的預測誤差比較

VC，BP，SVR，BMA不同模型誤差如圖4所示，誤差大部分在[-0.4，0.4]范圍波動，其中Vine Copula模型平均誤差較接近于0軸，但是個別誤差偏離0軸較大；BP和SVR模型誤差分布比較均勻，偏離0軸較大，使得預測精度較低；而BMA(VC，BP，SVR)模型的誤差分布偏離0軸較小，誤差分布比較均勻，圍繞平均值上下波動。從整體看BMA(VC，BP，SVR)模型能夠綜合各模型優勢，穩定準確地預測杞麓湖水位變化。

圖4 (VC，BP，SVR)不同模型預測誤差分布

為了驗證BMA方法對預測效果的提升，還構建了BMA(BP，SVR)模型，誤差統計指數如圖5所示。可看到BMA(BP，SVR)模型ME，RMSE，IA，NSE值分別為0.01，0.163，0.989，0.953，預測精度高于單一模型BP和SVR模型。水位過程線對比如圖6所示，可看到BMA(BP，SVR)(R=0.98)模型偏離實測水位較小，更接近于實測水位的峰值點和極值點。總體而言，不管BMA(VC，BP，SVR)模型還是BMA(BP，SVR)模型的預測精度都大于單一模型，對水位特征捕捉更充分，也進一步說明了BMA在多模型預測中提高預測精度的優越性。

圖5 (BP，SVR)不同模型對實測值的泰勒圖

圖6 (BP，SVR)不同模型逐月水位預測值與實測值時間序列對比圖

2.2 不確定性分析

基于區間寬度和覆蓋率兩個指標對BMA(VC，BP，SVR)模型預測序列的95%置信區間來分析結果的不確定性，評估模型性能。水位實測值(Z)、BMA(VC，BP，SVR)水位預測序列以及95%水平的置信區間如圖7所示，可看到95%置信區間內有大部分的水位實測值，只有66個值在不確定性區間外，其水位實測值的區間覆蓋率達90%，表明95%置信區間效果較好，不確定性較小。總體上可以看出，BMA(VC，BP，SVR)在濕季(5—10月)有56個實測值在置信區間外，而干季(11月—次年4月)只有10個實測值在置信區間外，且濕季的區間寬度比干季的大，說明水位預測精度在干季要高于濕季，且濕季水位預測的不確定性較大，還需要從模型結構中關于濕季的預測方法進一步改進。濕季水位預測不確定性較大的原因可能是濕季降水比較多，降水和入湖徑流各月份之間波動較大，3個模型不能對這一降雨徑流過程進行準確、有效地描述，由此造成濕季預測結果的偏差。

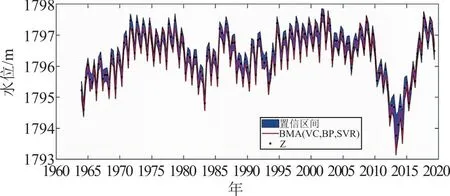
圖7 BMA(VC，BP，SVR)模型預測逐月水位的95%不確定性區間

3 結語

在流域各類用水消耗信息缺失條件下，利用降水、溫度、蒸發、徑流以及前1月水位作為水位的預測因子構建Vine Copula、BP和SVR模型獲得水位預測值，基于貝葉斯統計理論將機器學習模型和統計動力學模型結合構建BMA(VC，BP，SVR)和BMA(BP，SVR)模型，并應用到杞麓湖來提高長時序湖泊水位預測精度和不確定性分析。

(1)BMA方法都能夠在一定程度上集合不同模型優勢，提高預測精度。BP和SVR模型對時間序列的局部特征捕捉能力較強，Vine Copula模型對時間序列的時序特征描述更好，BMA(VC，BP，SVR)和BMA(BP，SVR)模型預測精度高于單一模型，但還是對一些峰值捕捉不好。

(2)95%置信區間表明，BMA(VC，BP，SVR)模型區間覆蓋率達90%，不確定性較小。

(3)濕季降水比較多，降水和入湖徑流各月份之間波動較大，BMA(VC，BP，SVR)模型濕季水位預測精度低于干季，且不確定性較大。

(4)在進行流域長時序水位預報時，考慮影響水位變化的物理基礎和各因素并選擇合適的預報因子，同時綜合多種預報方法，可有效降低長期水位預報的不確定性。此外，研究采用預見期為1個月，可滿足多模型綜合預報方法在該研究區有效性的論證，而該方法在不同預見期的有效性可能會有所區別，還需結合實際調度需求進一步檢驗，探索不同預見期下的最優預報方案，以更加合理地指導水位調度。