穿越煤系地層隧道預留巖墻破壞力學行為與安全厚度研究

許煜林, 邸小勇, 鞏 雯, 林 志, 李哲宇, 楊紅運

(1. 重慶交通大學 山區(qū)橋梁及隧道工程國家重點實驗室, 重慶 400074;2. 重慶高速工程顧問有限公司, 重慶 404100)

0 引言

我國經(jīng)濟快速發(fā)展,公路隧道的數(shù)量隨著公路里程的增加在逐年增加,2022年公路的總里程相對于2021年同比增長了1.38%,2019年隧道數(shù)量相對于2018年同比增加了6.80%。我國很多地區(qū)地形地貌復雜,需要通過修建公路隧道來減輕公路穿越這些復雜地形地貌的修建難度。在修建隧道的過程中會穿越一些特殊地質(zhì)條件復雜區(qū)域,如瓦斯地層、巖溶地層等,容易引發(fā)煤與瓦斯突出、突泥涌水等工程安全問題,可能造成嚴重的工程事故[1-2]。

在隧道建設過程中,原則上應該避免穿越瓦斯煤層等不良地質(zhì)帶,但往往由于多種原因,必須穿越瓦斯煤層時,將會面臨煤與瓦斯突出等一系列安全問題。若在隧道揭煤前對于煤與瓦斯突出沒有充分的防護準備,不但會發(fā)生事故,還會增加施工費用,造成工期延誤。

研究隧道揭煤過程中預留巖墻的力學規(guī)律變化,對穿越煤層的交通隧道具有一定的安全意義。本文使用相似試驗的方法得到2種不同跨度隧道預留巖墻的破壞時的力學性能變化,可為穿越煤層的其他存在煤與瓦斯突出風險的隧道提供巖墻破壞時的力學變化規(guī)律以及塑性破壞區(qū)的演化規(guī)律。

自20世紀50年代以來,學者們紛紛進入實驗室,深入研究煤與瓦斯的突出特性,以期揭示其形成的原因。例如: Skochinski[3]首次在實驗室中進行了煤與瓦斯的突出試驗;Yartsev[4]在實驗室中取得了與實際工程中類似的突出結果;Ujihira等[5-8]通過使用煤粉和加氣劑制作膠泥狀煤體,并進行了試驗,結果表明,當煤體暴露在表面時,瓦斯壓力會發(fā)生顯著的變化;Bodziony等[9-11]的試驗結果表明,當瓦斯壓力超過煤體的抗拉強度時,就會導致煤與瓦斯的突出。

21世紀初,蔡成功[12]為了模擬不同煤層強度、不同應力大小以及瓦斯壓力等條件下煤與瓦斯突出的過程設計了三維試驗裝置,得到應力大小和煤層力學性質(zhì)決定了突出強度;許江等[13-15]、尹光志等[16-17]、李曉泉等[18]、王維忠等[19]制作了煤與瓦斯突出大型模擬試驗裝置,可以進行均布荷載和階梯荷載的加載,對不同傾角的煤層進行煤與瓦斯突出試驗,之后在試驗裝置加裝了溫度和瓦斯壓力傳感器等,可以監(jiān)測煤與瓦斯突出過程中煤層內(nèi)部溫度變化和瓦斯壓力變化;王剛等[20]研發(fā)了能夠綜合考量瓦斯壓力、地應力和煤層結構的煤與瓦斯突出的模擬試驗裝置,并進行石門揭煤試驗。上述試驗對煤與瓦斯的突出進行了控制和重復性試驗,力學加載系統(tǒng)的穩(wěn)定性和可調(diào)性有了較大的改進,監(jiān)測系統(tǒng)的精密性也有了很大提高,為深入認識突出過程提供了有利條件,對瓦斯的發(fā)生和發(fā)展過程進行了研究,積累了寶貴的經(jīng)驗。但上述研究多是對煤礦施工進行試驗,而對于大斷面公路隧道的揭煤試驗研究還較少,且缺乏考慮不同地質(zhì)條件對煤與瓦斯突出的影響。

我國隧道規(guī)模不斷增長,其中穿越煤系地層的瓦斯隧道數(shù)量也在增加,但交通隧道的煤與瓦斯突出防治措施與理論相較于煤礦防突措施還不夠完善,需要進行進一步的完善研究。本文將基于建立的隧道石門揭煤試驗模型,結合相似理論和地質(zhì)力學模型,在實驗室中構建預留巖墻破壞試驗平臺,進行煤與瓦斯突出隧道預留巖墻破壞力學行為的相似模型試驗,研究預留巖墻發(fā)生破壞時的力學特性,通過數(shù)值模擬研究得到隧道揭煤過程中的預留巖墻安全厚度以及隧道揭煤過程中的預留巖墻集中應力區(qū)域以及巖墻厚度,為隧道穿越煤系地層提供施工安全保證和安全監(jiān)測參考。

1 工程背景

本文依托貴州省正安—習水高速公路天城壩隧道工程,天城壩位于遵義市習水縣仙源鎮(zhèn)北約5.50 km。根據(jù)《貴州省習水縣天成煤礦資源儲量核實與補充地質(zhì)勘探報告》,天城壩隧道工程區(qū)內(nèi)含煤地層為二疊系上統(tǒng)龍?zhí)督M,有泥巖、砂質(zhì)泥巖、泥質(zhì)粉砂巖、細砂巖夾數(shù)層薄層灰?guī)r、泥質(zhì)灰?guī)r、燧石灰?guī)r、煤層及鋁質(zhì)泥巖組成,屬海陸過渡帶局限海碳酸鹽臺地潮坪成煤環(huán)境。天城壩隧道煤系地層分布如圖 1所示。該處地質(zhì)構造復雜,巖層產(chǎn)狀變化較大,巖層傾角一般為27°～42°。煤層數(shù)量多,厚度變化大,最厚達到11.2 m;瓦斯質(zhì)量分數(shù)高,C8-2號煤層瓦斯質(zhì)量分數(shù)為21 m3/t;瓦斯壓力大,最大達到6.77 MPa。天城壩隧道地質(zhì)結構復雜、瓦斯質(zhì)量分數(shù)高、煤與瓦斯突出可能性大,在貴州乃至全國都是非常典型的。本文穿越煤系地層隧道施工方法采用中隔壁法(CD 法)開挖施工。為了盡可能地模擬現(xiàn)場的真實情況,模型試驗也采用中隔壁法(CD 法)開挖施工進行模型試驗隧道的開挖。

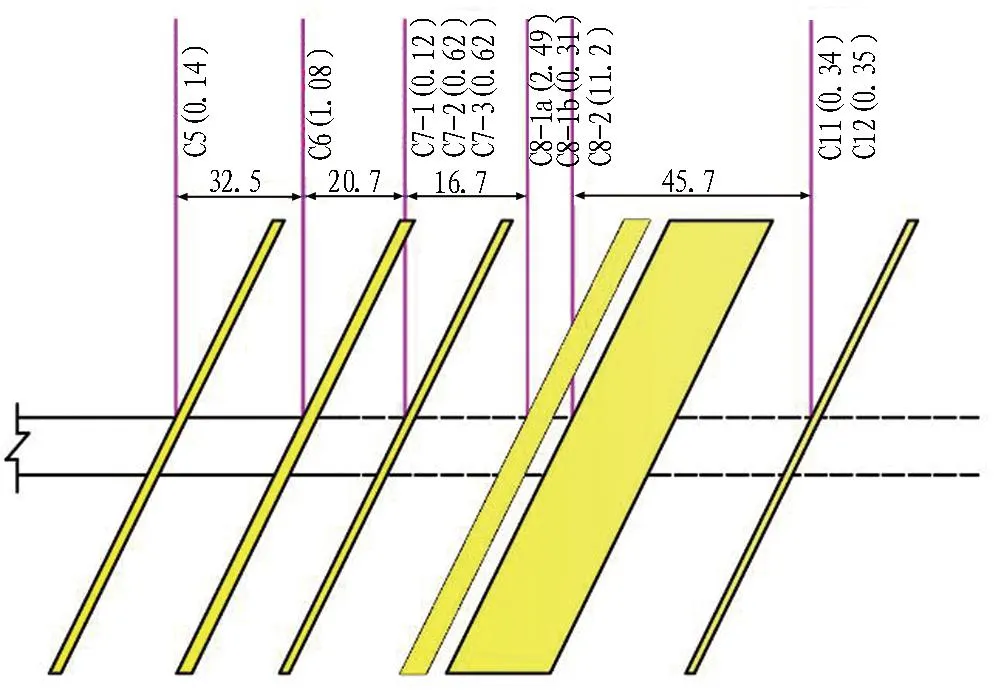
C5—C12表示隧道穿越的瓦斯煤層。

2 試驗方案設計

2.1 模型試驗系統(tǒng)

本試驗以貴州天城壩隧道所處地層條件進行試驗箱的設計,試驗模型的縮尺比例為1∶60。考慮到隧道開挖跨度影響系數(shù)、隧道荷載等效高度、邊界約束效應,本縮尺模型試驗采用2.6 m×2 m×1. 2 m(長×寬×高)的試驗箱。試驗模型箱示意如圖2所示。

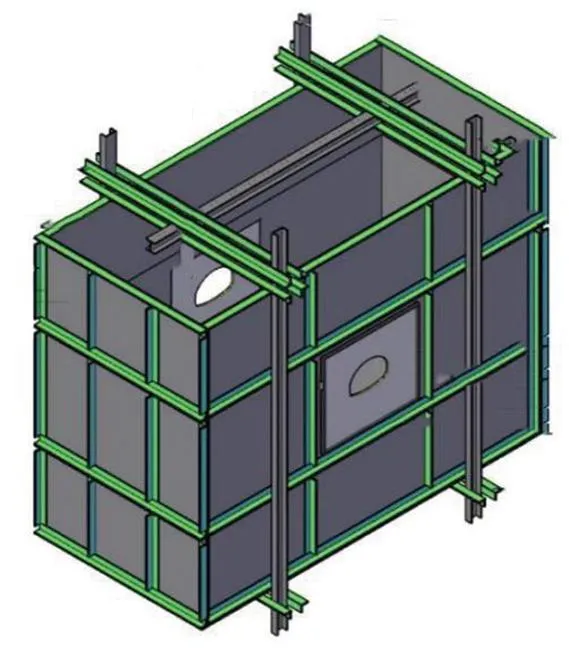
圖2 試驗模型箱示意圖

為了模擬實際工程中瓦斯隧道的高壓氣體狀態(tài),同時保證試驗的安全性,本試驗使用沒有爆炸危險的CO2氣體代替瓦斯氣體,通過控制CO2鋼瓶的輸出壓力閥來控制CO2噴出的壓力,進而模擬隧道瓦斯煤層吸附的瓦斯在開挖后大量釋放出的瓦斯氣體對前方預留巖墻的作用。其中,鋼瓶中的CO2氣體壓力為5 MPa。充氣裝置示意如圖 3所示。

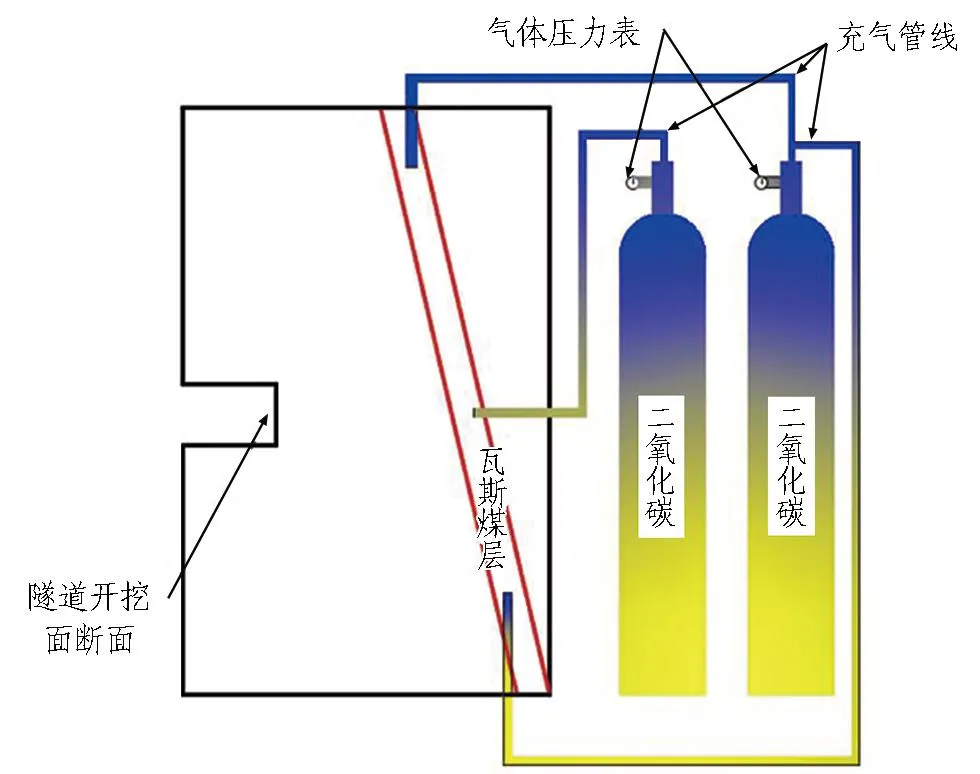
圖3 充氣裝置示意圖

箱體的頂板是一個可以活動的板,在此頂板放上液壓千斤頂進行地應力加載。依托工程天城壩隧道在穿越瓦斯煤層工區(qū)的隧道埋深取均值400 m,此時模型隧道上方的補充地應力按相似理論計算為0.13 MPa,最終本試驗選用的液壓千斤頂?shù)囊簤罕玫纳舷逓?00 MPa,液壓千斤頂能達到的最大力為500 kN,且本試驗所設計的反力架能夠在15 MPa的壓力下不出現(xiàn)明顯的形變。

2.2 試驗相似比常數(shù)的確定

模型試驗是否能取得成功,其相似材料參數(shù)的合理性是試驗的關鍵因素。本試驗對隧道所處原巖相似材料的彈性模量、內(nèi)摩擦角、泊松比等參數(shù)都應與隧道所處真實圍巖的對應參數(shù)范圍滿足相似理論關系。通過其相似理論得到各參數(shù)的相似常數(shù),其隧道所處巖體的物理力學參數(shù)也可以由上述相似比求得。隧道圍巖和圍巖相似材料物理力學參數(shù)如表1所示。

表1 隧道圍巖和圍巖相似材料物理力學參數(shù)

為達到相似模型材料全相似和縮小模型尺度的目的,根據(jù)前人的試驗和參考文獻,巖體相似材料的配置需要骨料作為填充材料,同時加上膠結材料作為黏結劑。結合相關文獻和試驗經(jīng)驗,確定正交試驗各因素水平如表2所示。

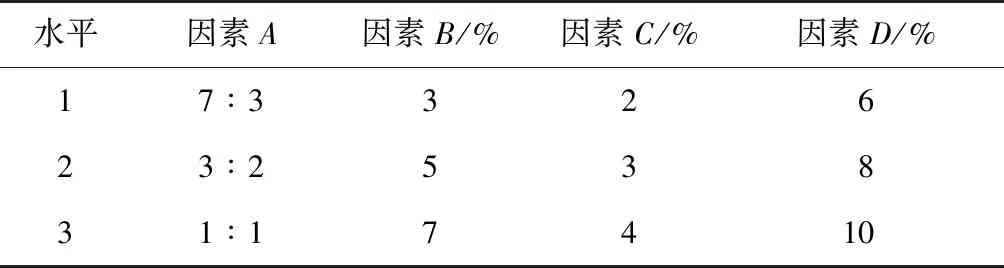
表2 正交試驗各因素水平

為了對相似材料進行直剪試驗從而測定材料的內(nèi)摩擦角和黏聚力,使用3D打印直徑61.8 mm×20 mm的圓柱試件模具。直剪試驗每組需3個試件,9組試驗需要制備27塊試件。

在完成試件制作后對其進行稱重并記錄其質(zhì)量,然后根據(jù)公式ρ=m/V求得試件密度,在此基礎上使用直剪試驗儀對其進行抗剪強度的測定。

通過直剪試驗可知,調(diào)整試驗相似材料石膏、土砂比、含水量以及凡士林的含量,使其黏聚力、摩擦角、重度更加靠近模擬巖體參數(shù)的值,最終得到直剪試驗的配合比下圍巖相似材料的性質(zhì)滿足理想圍巖相似材料的試驗要求,即該配合比的粉砂比為5∶5,石膏質(zhì)量占比為5%,凡士林質(zhì)量占比為2%,水質(zhì)量占比為15%。

2.3 模型體制作及監(jiān)測點布置

為收集隧道開挖過程中圍巖的應力、應變等力學參數(shù),從而得到圍巖的力學特性,在試驗模型開挖隧道的范圍內(nèi)按照一定的位置埋設多種監(jiān)測裝置,主要有應變片、位移計、土壓力盒。

2.3.1 應變采集監(jiān)測設備

由于本試驗測量的是掌子面前方預留巖墻的應變,沒法直接在巖墻上貼上應變片,故為了方便試驗數(shù)據(jù)的采集,按照模擬巖體的相似材料配比制作若干個3 cm×3 cm×3 cm的立方體方塊,并將應變片用氯丁膠粘貼在立方體表面,用作測量預留巖墻的應變。應變采集點布置如圖4所示。用于采集隧道開挖時發(fā)生突出前預留巖墻的應變值,從而獲得圍巖所受的應力。

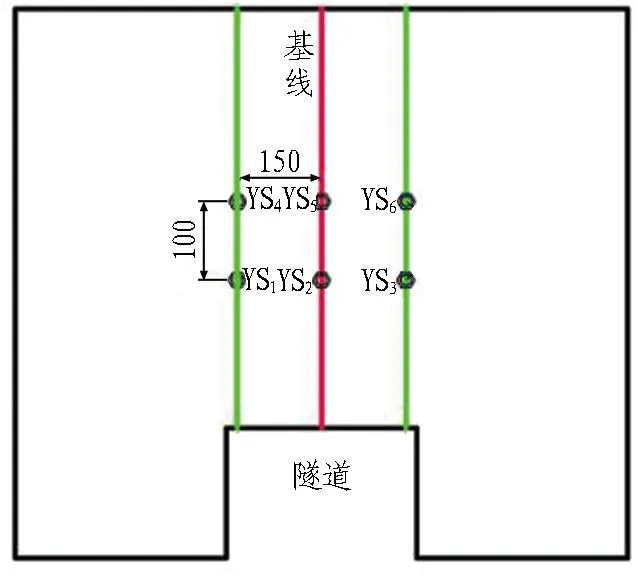
(a) 俯視圖

(a) 側視圖

2.3.2 位移監(jiān)測重采集設備

位移監(jiān)測點布置如圖5所示。在隧道上方每隔200 mm安裝3排位移監(jiān)測點,每排設置2個位移計,位移計應盡量靠近箱體壁面,并且每個位移計之間保持200 mm的距離,主要用于收集隧道開挖過程上部圍巖的變形情況。

W1—W6表示隧道上方所在監(jiān)測平面的位移采集監(jiān)測點。

2.3.3 壓力監(jiān)測采集設備

在預留巖墻靠近煤層瓦斯充氣點的位置設置2組壓力的傳感器,主要用于監(jiān)測開挖過程中突出前后預留巖墻壓力的演變情況。壓力監(jiān)測傳感器布置示意如圖 6所示。

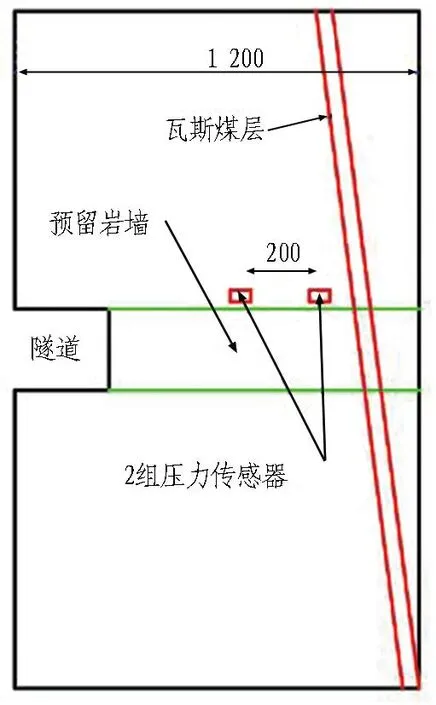
(a) 土壓力盒縱向布置圖

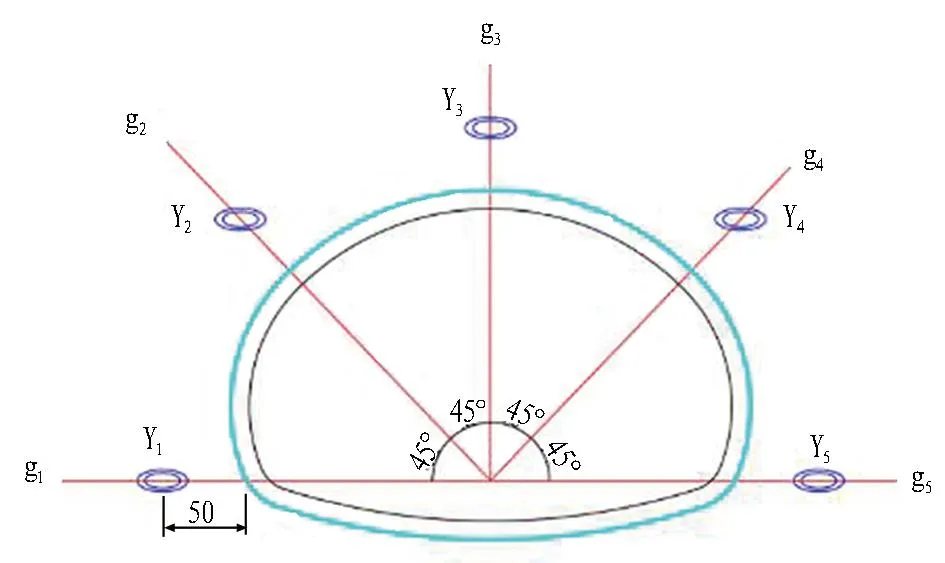
(a) 土壓力盒環(huán)向布置圖

2.4 模擬試驗流程

模型試驗流程如圖 7所示。

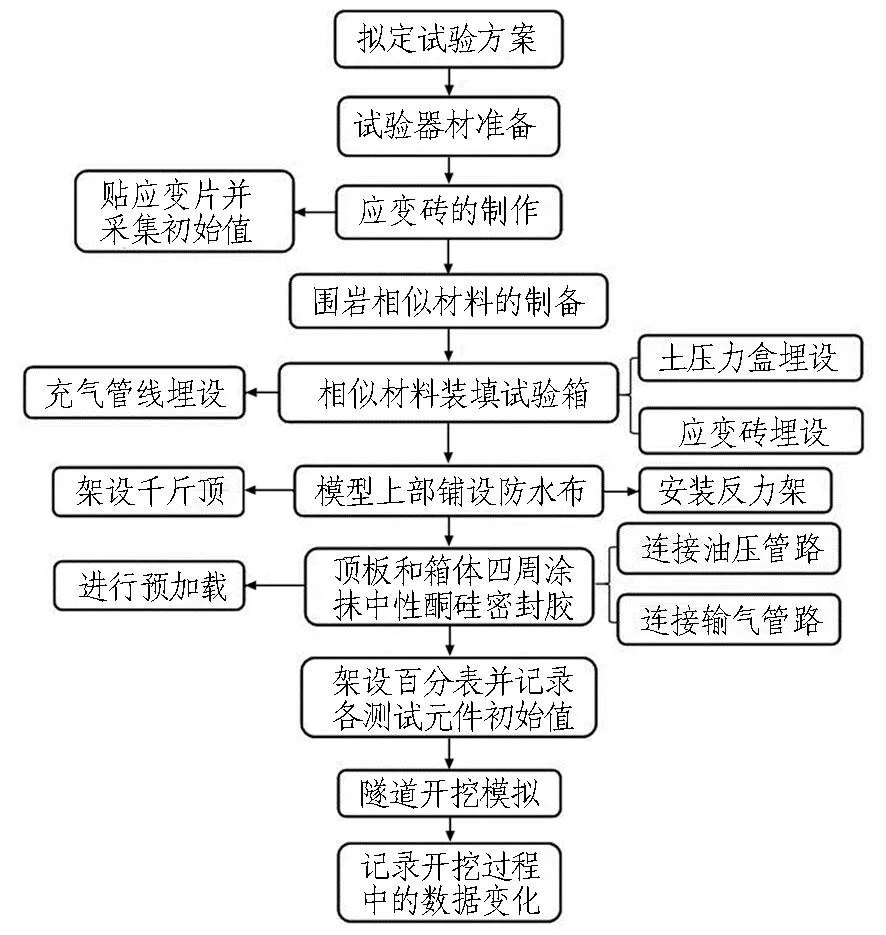
圖7 模型試驗流程圖

3 試驗結果

3.1 預留巖墻的應力分析

不同跨度巖墻應力變化情況如圖8所示。

由圖 8(a)和圖 8(b)可以看出: 1)在2種不同跨度的隧道開挖過程中,垂直應力的變化規(guī)律都是先增大后減小。其開挖過程中的垂直壓力變化規(guī)律的原因歸于地應力和開挖造成的應力集中會增加圍巖的裂隙,降低了巖墻的強度,高壓的CO2使巖墻中裂隙充斥著CO2氣體,從而使圍巖中的垂直壓力呈逐步緩慢增加的趨勢,隨著隧道開挖的進行,圍巖巖墻的厚度逐漸變小使CO2氣體得到釋放,圍巖中的垂直應力得到釋放,釋放的程度取決于開挖的距離。2)當隧道開挖跨度由14.3 cm增加到18 cm后,測點YX1、YX2、YX3達到最大垂直應力的開挖距離由17 cm縮短到15 cm;YX4、YX5、YX6測點達到最大垂直應力的開挖距離由30 cm縮短到25 cm,平均減小了14.15%;且發(fā)生應力突變導致巖墻破壞的開挖距離由40 cm縮短到35 cm,說明開挖跨度增大后,隧道掌子面前方預留巖墻的安全厚度增加了12%;各測點最大垂直應力增大了12%。

由圖 8(c)和圖 8(d)可以看出: 1)當隧道開挖跨度由14.3 cm增加到18 cm后,測點YX1、YX2、YX3的最大水平應力由0.32 MPa增加到0.45 MPa,增大了28.8%;測點YX4、YX5、YX6由0.52 MPa增加到了0.68 MPa,增大了23.5%,說明當跨度增大后預留巖墻的水平應力平均增大了26%。2)在開挖跨度為14.3 cm時,垂直應力最大值是水平應力最大值的1.28倍;開挖跨度增大到18 cm時,垂直應力最大值是水平應力最大值的1.17倍。

(a) 跨度為14.3 cm時的垂直應力變化

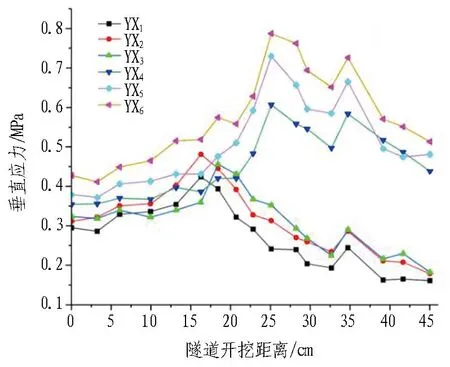
(b) 跨度為18 cm時的垂直應力變化

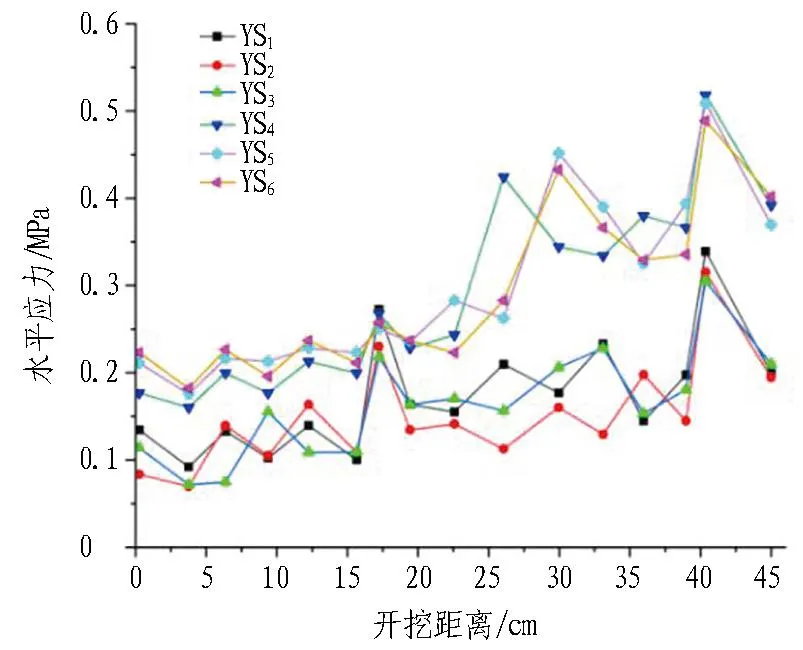
(c) 跨度為14.3 cm時的水平應力變化

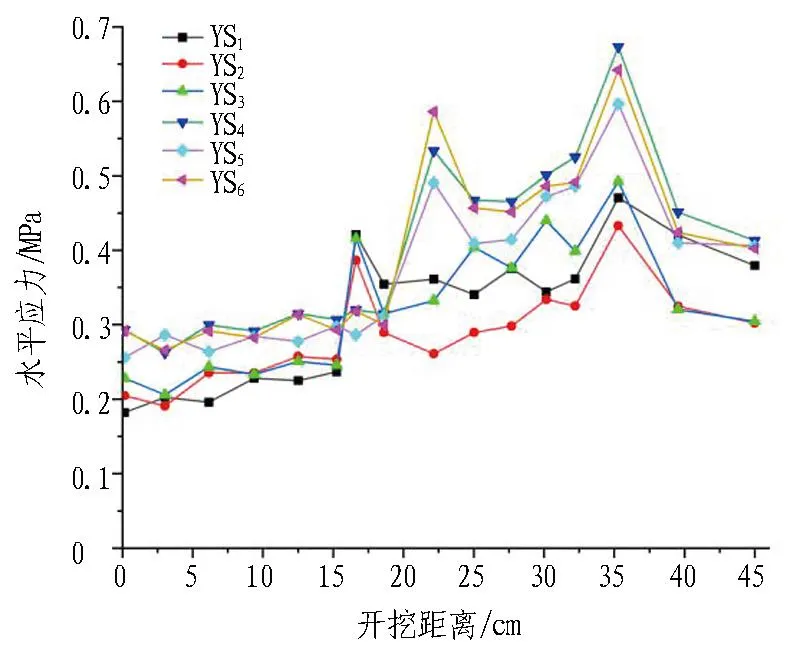
(d) 跨度為18 cm時的水平應力變化

3.2 預留巖墻的四周圍巖壓力分析

不同跨度預留巖柱四周圍巖壓力如圖 9所示。可以看出: 1)當隧道開挖跨度由14.3 cm增加到18 cm時,拱頂?shù)淖畲髧鷰r壓力由0.35 MPa增加到0.6 MPa,增大了41%;左拱腳的最大圍巖壓力由0.22 MPa增加到0.35 MPa,增大了37%;左拱腰的最大圍巖壓力由0.22 MPa增加到0.25 MPa,增大了12%;右拱腳的最大圍巖壓力由0.25 MPa增加到0.39 MPa,增加了35%;右拱腰的最大圍巖壓力由0.26 MPa增加到0.39 MPa,增加了33%。說明隧道開挖跨度增大后,預留巖墻四周圍巖壓力在拱頂和拱腳處增大的較為明顯,預留巖墻在拱頂和拱腳處更容易發(fā)生破壞。2)開挖跨度越大,隧道圍巖的破壞時的巖墻厚度也越大,在施工中大跨度的隧道要預留足夠的巖墻厚度,以保證施工的安全。

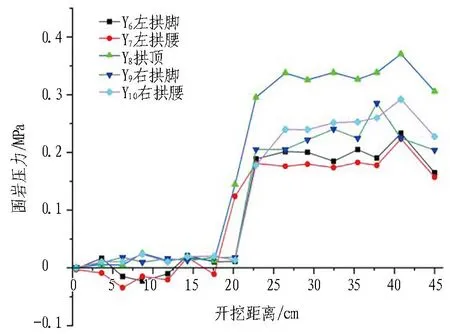
(a) 跨度為14.3 cm時的圍巖壓力變化

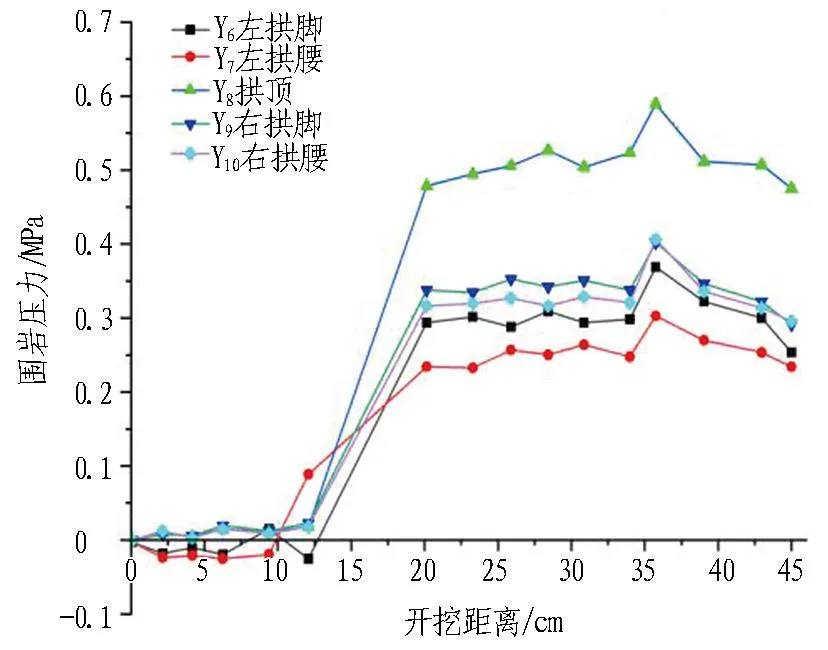
(b) 跨度為18 cm時的圍巖壓力變化

3.3 預留巖墻的拱頂沉降分析

不同跨度位移變化如圖10所示。可以看出: 1)當隧道開挖跨度由14.3 cm增加到18 cm時,W2測點穩(wěn)定時的位移變化量由11 mm增加到13 mm,增加了15.4%;W5測點穩(wěn)定的位移變化量由13 mm增加到16 mm,增加了18.7%。位移平均增長了17.1%,說明當隧道開挖跨度增加后,預留巖墻的變形量更大,需要增加預留巖墻的厚度防止其發(fā)生破壞。2)隨著隧道的開挖,掌子面前方的預留巖墻垂直應力開始增大時,對應的位移監(jiān)測點的豎向位移開始增大;當掌子面前方的預留巖墻的垂直應力達到最大值時,位移監(jiān)測點監(jiān)測到的豎向位移變形也達到最大值;隨著隧道繼續(xù)向前開挖,預留巖墻的垂直應力開始減小,位移監(jiān)測點監(jiān)測到的豎向位移變形開始逐漸穩(wěn)定;最后垂直應力發(fā)生突變時,掌子面前方預留巖墻發(fā)生破壞,隧道位移監(jiān)測點的位移量發(fā)生突變,快速增大。

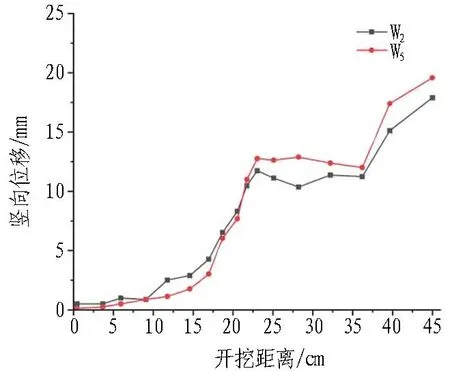
(a) 跨度為14.3 cm時圍巖位移變化

(b) 跨度為18 cm時圍巖位移變化

4 氣-固耦合作用下巖墻預留厚度的數(shù)值模擬

4.1 數(shù)值模型的建立

本文利用comsol數(shù)值模擬軟件,選取天城壩隧道ZK110+295～+445標段作為依托背景,其埋深平均深度為450 m。幾何模型設置為50 m(寬)×70 m(高),其隧道開挖跨度為10、11.04、16.03 m,開挖步長為4 m,隧道開挖方式設置為中隔壁法(CD 法)開挖施工。模型四周設置為不透氣邊界層,上邊界為應力補充荷載,將上部的巖石重力轉(zhuǎn)換為均布荷載作用到模型上邊界,其荷載大小為5 MPa。模型左右邊界為輥支撐,模型中圍巖的塑性變形使用Mohr-Coulomb本構模型,將材料簡化為均一介質(zhì)模型且具有各向同性。基于comsol數(shù)值模擬軟件建立隧道幾何模型,網(wǎng)格采用comsol中內(nèi)置的自動細化網(wǎng)格劃分來優(yōu)化網(wǎng)格劃分,同時對隧道開挖位置進行局部的加密處理。幾何模型如圖 11所示。

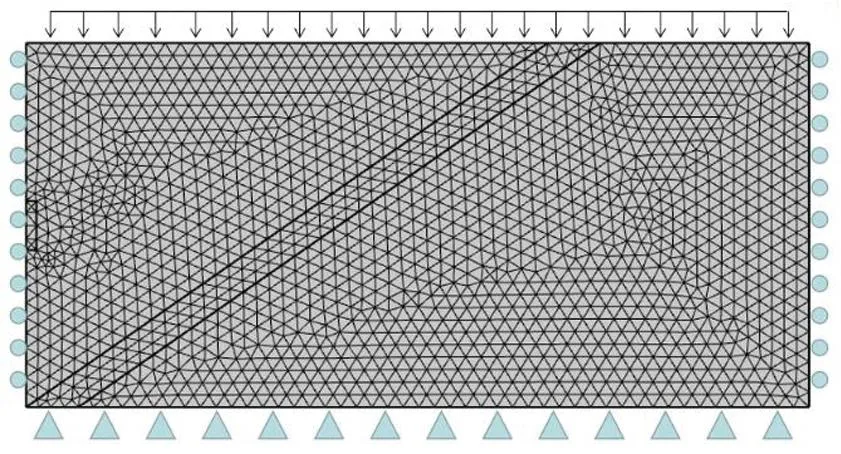
圖11 幾何模型

4.1.1 模型參數(shù)的確定

圍巖物理參數(shù)如表 3所示。瓦斯氣體物理力學參數(shù)如表4所示。

表3 圍巖物理參數(shù)

表4 瓦斯氣體物理力學參數(shù)

4.1.2 模擬工況的確定

依托工程天城壩隧道煤層的瓦斯壓力為2～3 MPa。通過相關文獻的研究以及相關規(guī)范《公路瓦斯隧道設計與施工技術規(guī)范》[21]的查閱可知,當煤層的瓦斯壓力大于0.74 MPa時,則認為煤層具有發(fā)生瓦斯突出的風險。為了更好地反映不同因素對于瓦斯隧道預留安全巖墻厚度的影響,本文按照圍巖等級、瓦斯壓力以及隧道開挖跨度進行了不同工況的設置,其中瓦斯壓力的變化模數(shù)取2.00 MPa,將其劃分為 0.74、2.00、4.00 MPa。

為了考慮不同跨度對隧道預留巖墻厚度的影響,根據(jù)規(guī)范《公路隧道設計細則》對公路隧道建筑限界橫斷面組成最小寬度以及支護和預留變形量的要求,分別選取三級公路(40 km/h) 2車道、一級公路(100 km/h) 2車道、一級公路(120 km/h) 3車道3個不同跨度進行研究。三級公路2車道跨度為10.00 m、高度為7.85 m;一級公路2車道,跨度為11.40 m、高度為8.7 m;一級公路3車道,跨度為16.03 m、高度9.8 m。由于本文數(shù)值模擬為二維結構模型,數(shù)值模擬中取的是不同跨度隧道的斷面高度進行數(shù)值計算。不同工況的參數(shù)設置如表 5所示。

表5 不同工況的參數(shù)設置

本次數(shù)值模擬中選擇3個影響隧道開挖掌子面前方與瓦斯煤層間預留巖墻厚度的因素,并且根據(jù)正交試驗的原理設置模擬工況,用以分析3個不同因素對預留巖墻穩(wěn)定性和厚度的影響。正交工況的設置如表6 所示。

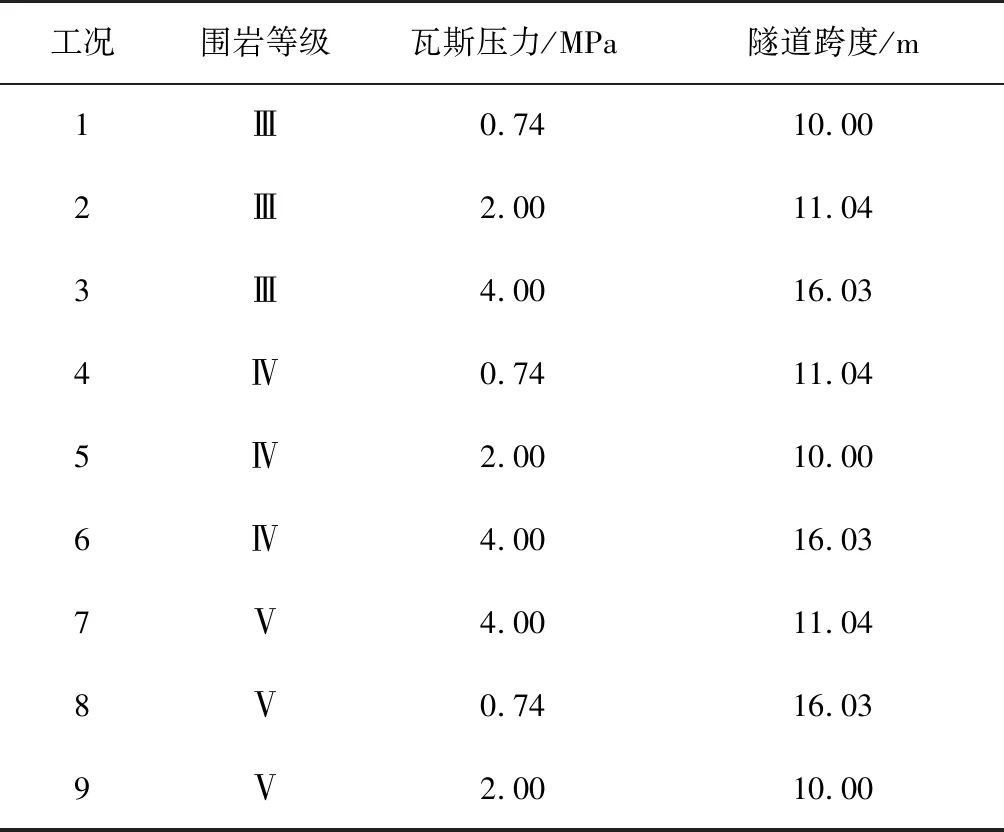
表6 正交工況的設置

4.2 模型計算結果分析

4.2.1 預留巖墻最小厚度分析

確定隧道掌子面與煤系地層間預留巖墻的最小安全距離,需要判斷隧道預留巖墻的穩(wěn)定性。其穩(wěn)定性判定依據(jù)主要有應力等值線、圍巖的塑性形變和位移以及圍巖的破壞區(qū)等因素。對9種工況下的隧道進行數(shù)值模擬,得到9種工況下瓦斯煤層與掌子面之間預留巖墻的最小厚度計算結果。不同工況下最小安全巖墻如表 7所示。

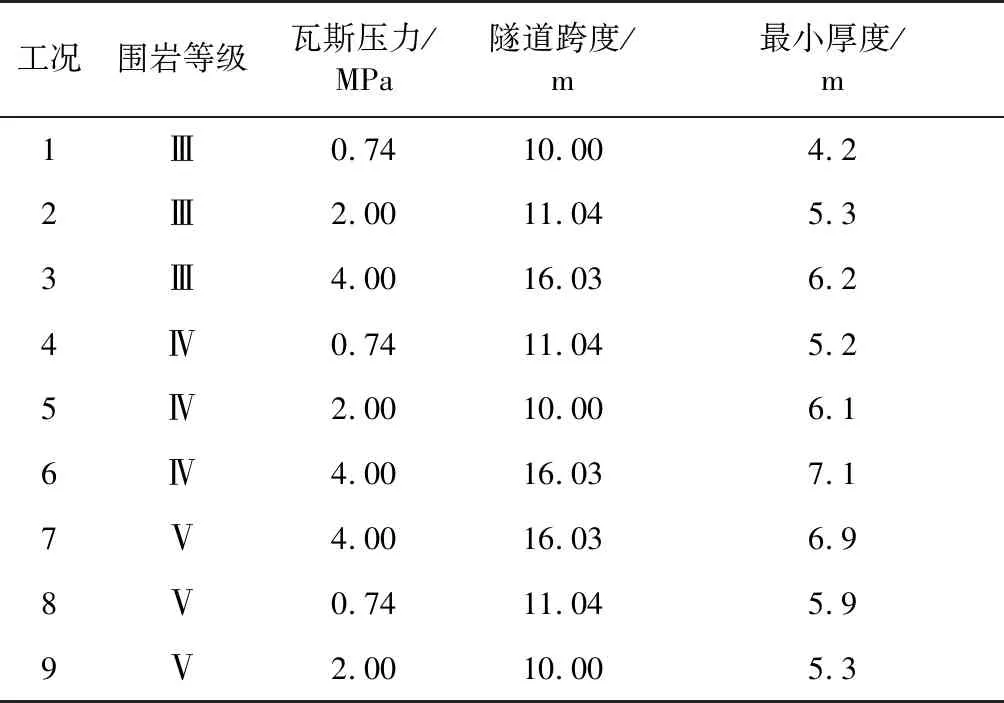
表7 不同工況下最小安全巖墻

通過對影響大斷面隧道預留巖墻最小厚度的不同因素進行極差分析,得到不同影響因素的極差R值。通過分析不同影響因素的極差R值與預留巖墻厚度之間的關系,來判斷其對巖墻最小厚度的影響程度。若R越大,則該因素對巖墻厚度的影響越大,也越重要,可以通過極差R值的大小進行主次因素的判斷。預留巖墻最小厚度影響因素極差分析如表8所示。

表8 預留巖墻最小厚度影響因素極差分析

若對應影響因素的極差較大,說明該因素對預留巖墻厚度的變化影響較大。由表 8可知: 安全巖墻厚度影響因素排序為瓦斯壓力、隧道跨度、圍巖等級,且瓦斯壓力和隧道跨度對預留巖墻厚度的影響相差不大。根據(jù)表8繪制出不同影響因素和巖墻最小厚度之間的關系變化趨勢,如圖 12所示。

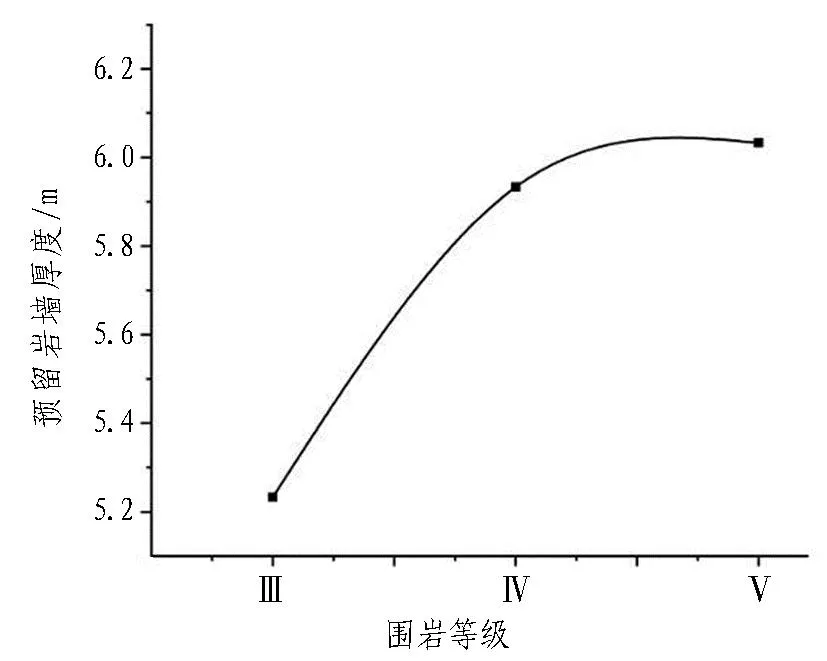
(a) 圍巖等級

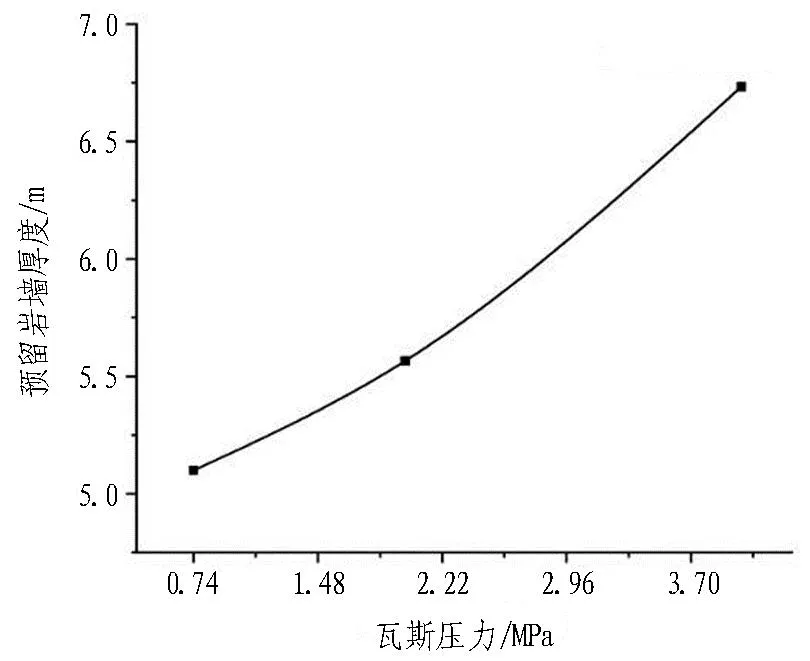
(b) 瓦斯壓力

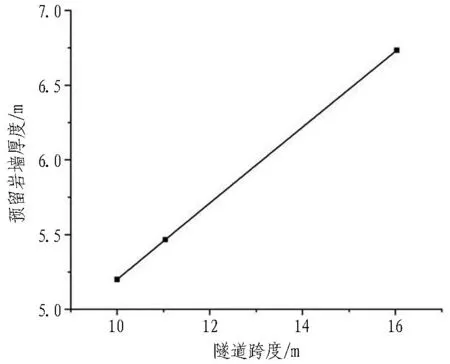
(c) 隧道開挖跨度

1)由圖12(a)可以看出: 當圍巖等級從Ⅲ級變到Ⅳ級和Ⅳ級變到Ⅴ級的增長率不相同,其Ⅳ級變到Ⅴ級的增長率顯著下降。對于Ⅳ級和Ⅴ級圍巖來說,圍巖的等級對預留巖墻厚度的影響變化不顯著。

2)由圖12(b)可以看出: 針對隧道瓦斯壓力,掌子面前方的預留巖墻厚度與瓦斯壓力的關系大致成二次函數(shù)關系,即當瓦斯壓力增大時,預留巖墻的厚度增大。煤層瓦斯壓力越大,對前方預留巖墻的塑性破壞影響越大,瓦斯壓力的增大會使預留巖墻的破壞區(qū)更容易貫穿煤系地層,導致隧道掌子面前方的預留巖墻發(fā)生破壞,為煤與瓦斯突出提供條件,因此預留巖墻的厚度隨著瓦斯壓力的增加呈線性變化,即瓦斯壓力越大預留巖墻越厚。

3)由圖12(c)可以看出: 掌子面前方預留巖墻厚度隨隧道跨度的增大而增大。因為隧道開挖斷面越大致使隧道的臨空面越大,從而應力的變化越大,圍巖的塑性破壞區(qū)也越大,且當隧道開挖跨度從10.00 m變化到11.04 m時預留巖墻的厚度增長率為4.88%;當隧道開挖跨度從11.04 m變化到16.03 m時預留巖墻的厚度增長率為18.81%。隧道開挖跨度的逐漸增大預留巖墻厚度的變化率也越大,開挖跨度對預留巖墻的厚度影響也越大。

4.2.2 預留巖墻厚度分析

根據(jù)上述極差分析結果,對預留巖墻的厚度和不同因素之間建立多元回歸模型進行分析。通過決定系數(shù)R2來反映模型擬合數(shù)據(jù)的準確程度。一般來說,R2為0～1,若其數(shù)值離1越近,說明該回歸模型對數(shù)據(jù)的擬合程度越好;其值越接近0,表明模型擬合的越差。一般來說R2>0.4,擬合效果較好。

4.2.2.1 隧道圍巖等級和預留巖墻厚度的一元回歸模型

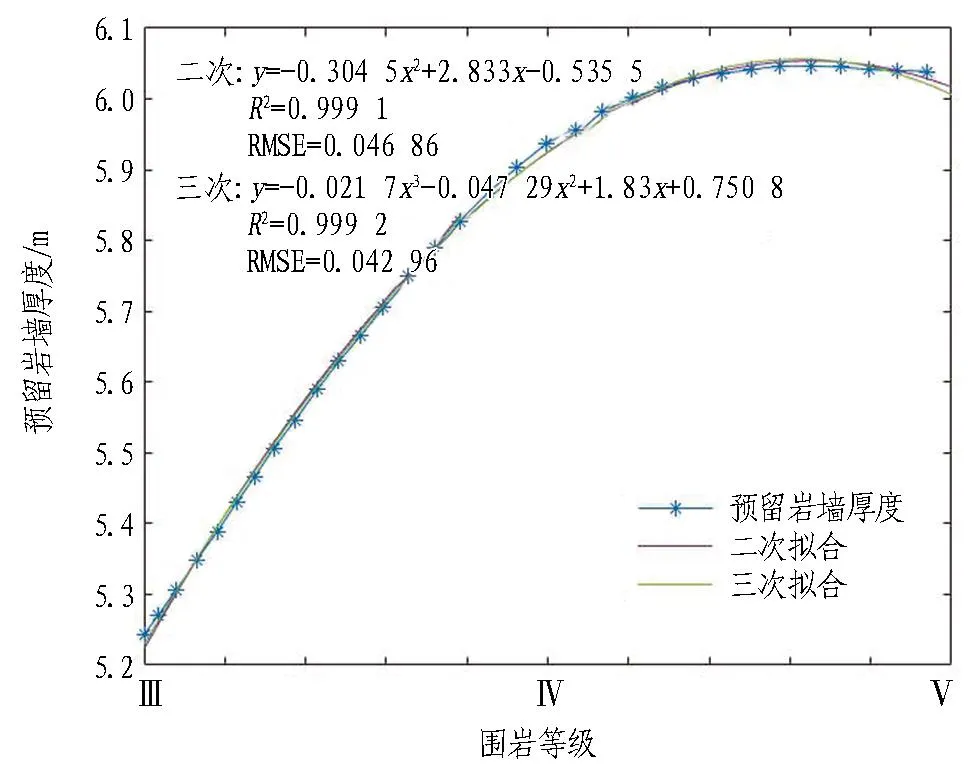
圍巖等級和巖墻厚度回歸模型如圖13所示。

二次擬合:y=-0.304 5x2+2.833x-0.535 5。

三次擬合:y=-0.021 7x3-0.047 29x2+1.83x-
0.750 8。

二次擬合相關系數(shù):R2=0.999 1。

三次擬合相關系數(shù):R2=0.999 2。

由圖 13可知: 1)隧道圍巖等級和預留巖墻厚度的回歸擬合模型中二次擬合和三次擬合的R2均大于0.4,即2種擬合程度均較好。2)其殘差圖中二次擬合和三次擬合的RMSE分別為0.046 856和0.042 964,且二者的殘差均是隨機分布在0線附近,即二者的殘差都落在0線這條變化幅度不大的直線之內(nèi),說明了2種擬合模型效果均很好。

(a) 圍巖等級和預留巖墻厚度的擬合圖

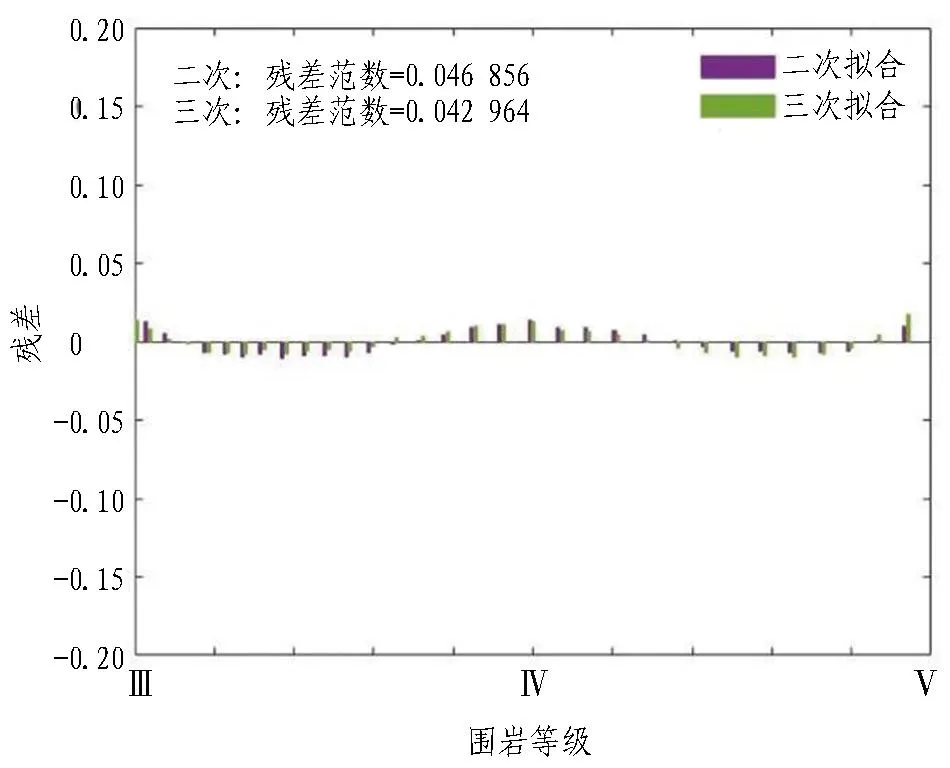
(b) 圍巖等級與巖墻厚度殘差圖

4.2.2.2 煤層瓦斯壓力與預留巖墻厚度的一元回歸模型

瓦斯壓力和巖墻厚度回歸模型如圖14所示。

線性擬合:y=0.513 7x+4.618。

二次擬合:y=0.068 63x2+0.196x+4.924。

線性擬合相關系數(shù):R2=0.987 4。

二次擬合相關系數(shù):R2=0.999 8。

由圖 14可知: 1)瓦斯壓力和預留巖墻厚度的回歸擬合模型中線性擬合和二次擬合的R2分別為0.987 4和0.999 8,數(shù)值均大于0.4,即2種擬合程度均較好。2)其殘差圖中線性擬合和二次擬合的RMSE分別為0.300 99和0.035 464,此時線性擬合的殘差為拋物線形,沒有均勻地分布在0線附近,說明線性擬合欠佳,模型結構不正確,模型中應該包含二次項。而對于二次擬合,其殘差圖中殘差都落在0線這條變化幅度不大的直線之內(nèi),說明了二次擬合模型效果好于線性擬合的模型效果。

(a) 瓦斯壓力和預留巖墻厚度的擬合圖

(b) 瓦斯壓力與巖墻厚度殘差圖

4.2.2.3 隧道開挖跨度與預留巖墻厚度的一元回歸模型

隧道跨度和巖墻厚度回歸模型如圖15所示。

線性擬合:y=0.255x+2.66。

線性擬合相關系數(shù):R2=0.999 9。

由圖 15可知: 1)隧道開挖跨度和預留巖墻厚度的回歸擬合模型中線性擬合R2為0.999 9,數(shù)值均大于0.4,即線性擬合程度較好。2)其殘差圖中線性擬合的RMSE分別為0.018 3,殘差均是隨機分布在0線附近,線性擬合的殘差在0線附近分布較為集中,且是均勻分布在0線附近,故線性擬合模型效果不錯。

(a) 隧道跨度和預留巖墻厚度的擬合圖

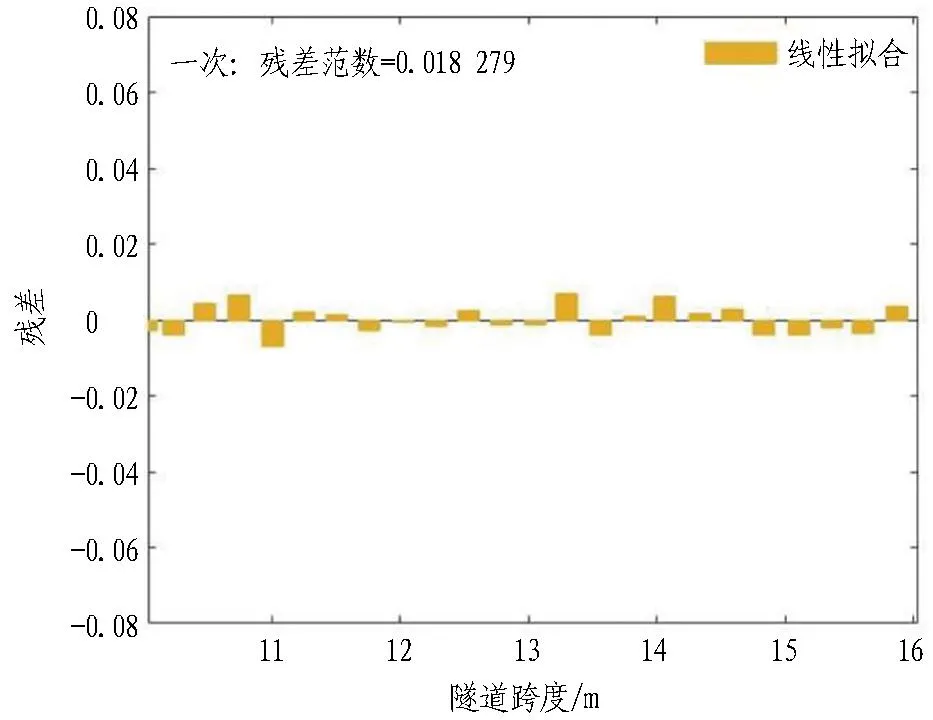
(b) 隧道跨度與巖墻厚度殘差圖

通過上述一元回歸分析,對影響預留巖墻厚度的因素建立多元回歸模型,基于以上分析將安全巖墻厚度結果導入 SPSS 軟件中,構建多元回歸模型

式中:y為預留巖墻的厚度;x1為隧道圍巖等級;x2為瓦斯壓力水平;x3為隧道開挖跨度。

在本數(shù)值計算中的巖體模型是理想化后的均一介質(zhì)模型,這與實際工程中的實際巖體情況有著一定的區(qū)別,因此對于多因素條件下的預留巖墻厚度的回歸擬合需要設定安全系數(shù)N,用以提高其安全性。通過文獻查閱,安全系數(shù)的取值一般為1.2～1.5[21-22],可得到預留巖墻厚度經(jīng)驗計算公式:

對上述預留巖墻厚度回歸式進行顯著性檢驗,結果如表9和表10所示。

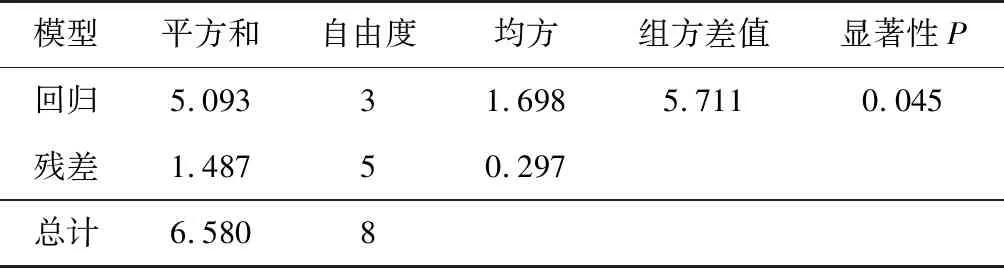
表9 預留巖墻厚度方差分析

由表9可知: 對多元回歸方程進行顯著性概率檢驗,P=0.045<0.05,則說明多元回歸模型中預留巖墻的厚度和瓦斯壓力、圍巖等級、隧道開挖跨度等自變量之間存在線性相關,且多元回歸方程相關性顯著。

表10 回歸系數(shù)表

由表10可知: 對于圍巖等級(b=0.400,β=0.382,P=0.032)、瓦斯壓力(b=0.085,β=0.134,P=0.035)、隧道跨度(b=0.240,β=0.740,P=0.021)均會影響預留巖墻的厚度,且圍巖等級、瓦斯壓力、隧道跨度均為正向預測(因為回歸系數(shù)b均為正)預留巖墻厚度,且顯著性概率P小于0.05,認為變量顯著。

共線性統(tǒng)計包括方差膨脹因子(VIF)和容差2個指標,事實上,VIF=容差的倒數(shù)(1/容差),只需要判斷其中1個指標即可。如果容差小于0.1(或方差膨脹因子大于10),提示數(shù)據(jù)存在多重共線性。在本研究中,所有容忍度值都大于0.1(最小值為0.9),說明本研究自變量多重共線不嚴重,影響因素和預留巖墻的厚度之間有較好的線性關系。

5 結論與建議

1)以遵義市天城壩隧道隧址區(qū)的F4斷裂層瓦斯煤層為工程背景,通過三維模型試驗模擬在不同跨度隧道開挖過程中遭遇瓦斯煤層和斷裂層時隨預留巖墻的厚度變化的全過程。隧道開挖改變了圍巖的原始應力狀態(tài),在隧道掌子面前方的巖墻出現(xiàn)應力集中,且隧道在開挖后掌子面一側的應力卸載使豎向應力和水平應力差值最大。同時通過摩爾-庫侖理論,巖墻容易發(fā)生破壞的區(qū)域為掌子面和其前方一定范圍內(nèi)的巖墻,越遠離掌子面破壞越小。

2)使用突變理論分析了巖墻的穩(wěn)定性,得出當隧道所在的地質(zhì)環(huán)境相同時,預留巖墻上部垂直地應力越大,隧道的開挖跨度越大,預留巖墻的厚度及彈性模量越小,預留巖墻發(fā)生破壞失穩(wěn)的可能性越大。

3)隨著隧道的開挖,掌子面前方的預留巖墻垂直應力開始增大時,對應的位移監(jiān)測點的豎向位移開始增大;當掌子面前方的預留巖墻的垂直應力達到最大值時,位移監(jiān)測點監(jiān)測到的豎向位移變形也達到最大值;隨著隧道繼續(xù)向前開挖,預留巖墻的垂直應力開始減小,位移監(jiān)測點監(jiān)測到的豎向位移變形開始逐漸穩(wěn)定;最后垂直應力發(fā)生突變時,掌子面前方預留巖墻發(fā)生破壞,隧道位移監(jiān)測點的位移量發(fā)生突變,快速增大。

4)通過數(shù)值模擬得到了在不同瓦斯壓力、圍巖等級等不同因素下的預留巖墻厚度的變化規(guī)律,通過多因素回歸算法擬合得到了巖墻厚度的最小經(jīng)驗公式。

5)根據(jù)天城壩隧道的實際工況進行計算可知,天城壩隧道在開挖過程中揭煤的最小預留巖墻厚度理論上應為5.9 m,在《公路瓦斯隧道設計與施工技術規(guī)范》[21]對防突措施要求檢驗的最小厚度為5 m,故對于隧道如果依據(jù)規(guī)范在5 m處進行瓦斯突出安全檢驗,發(fā)生煤與瓦斯突出的風險較高,因此需要增加預留安全巖墻檢驗厚度,從而降低煤與瓦斯突出的可能性。