GMA-型生物化學系統的參數估計方法




摘要:
研究生物化學系統的參數估計方法問題,給出了廣義質量作用(generalized mass action,GMA)-型生物化學系統的數學模型及其數學性質。為了估計GMA-型生物化學系統的模型參數,以極小化濃度誤差準則和斜率誤差準則之和為優化目標,以GMA-型生物化學系統及其模型參數允許范圍為約束,構建了一種參數估計優化模型,并設計出有效的計算方法求解構建的參數估計優化模型。數值計算與仿真結果表明,給出的GMA-型生物化學系統的參數估計方法可以獲得較為精確的模型參數估計結果。
關鍵詞:GMA-系統; 生物化學系統; 算法; 參數估計
中圖分類號:O29文獻標志碼:A
doi:10.3969/j.issn.1673-5862.2024.05.010
Parameter estimation method of GMA-type biochemical systems
XU Gongxian, HU Qiuxu
(School of Mathematical Sciences, Bohai University, Jinzhou 121013, China)
Abstract:
In this paper, a parameter estimation problem of biochemical system is studied. The mathematical model of GMA-type biochemical system and its mathematical properties are given. A parameter estimation optimization model is constructed to estimate the model parameters of GMA-type biochemical system.In this model, the minimization objective is the sum of the concentration error criterion and the slope error criterion, and the constraints include the GMA-type biochemical system and the ranges of model parameters. An effective computation method is designed to solve the constructed parameter estimation optimization model. The numerical computation and simulation results show that the parameter estimation method of GMA-type biochemical system in this paper can obtain more accurate estimation results for model parameters.
Key words:
GMA-system; biochemical system; algorithm; parameter estimation
為了深入研究生物化學系統的反應過程,需要構建生物化學系統的數學模型[1-2],并運用相應的數學語言和方法表示反應中各個變量的變化規律,進而探究生物化學系統的反應機理[3-4]。在利用數學模型模擬和控制實際工業生產過程時,模型的可信度和準確度至關重要。因此,尋找模型的最優參數(稱為參數估計或參數辨識[5-6])也就極為重要。在過去幾十年里,參數估計問題已經得到了廣泛的研究。例如Xu等[7]、Zhao和Xu[8]運用兩階段法研究了甘油生產1,3-丙二醇過程的參數估計問題;Task和Banerjee[9]基于整數規劃對S-型生物化學系統的參數估計進行了分析研究;文獻[10-12]應用智能優化算法研究了S-型生物化學系統的模型建立與參數估計問題;劉豐[13]基于三次樣條插值提出了一種可以估計非線性生物化學系統參數的估計方法;吳家琪和徐恭賢[14]基于基爾公式提出了一種可以有效求解參數估計問題最優解的迭代方法;徐恭賢等[15]基于龍格庫塔公式提出了一種可以估計S-型生物化學系統參數的有效方法。
目前,未見有關于廣義質量作用(generalized mass action,GMA)-型生物化學系統的參數估計方法研究。因此,本文針對這一類型系統,綜合考慮2個誤差函數之和,構建了一種參數估計優化模型,并提出了有效的求解方法對優化模型進行求解,獲得了GMA-型生物化學系統的最優參數值。2個數值算例表明本文所提方法能夠獲得較為精確的參數估計結果。
2GMA-型生物化學系統及其數學性質
考慮如下GMA-型生物化學系統:
dXidt=∑p+ij=1(α+ij∏n+me=1Xh+ijee)-∑p-ik=1(α-ik∏n+me=1Xh-ikee),t∈[0,T],i=1,2,…,nXi(0)=Xi0 (1)
其中:Xi(i=1,2,…,n)為代謝物濃度;Xe(e=n+1,n+2,…,n+m)為酶活性;α+ij,α-ik為速率常數;h+ije和h-ike為動力階。
令dXi/dt=fi(X,q),其中X=(X1,X2,…,Xn)T,q=((G+)T,(G-)T,(H+)T,(H-)T)T∈Qad,Qad是有界閉集,q中的G+,G-,H+,H-可分別表示為
G+=(α+11,α+12,…,α+1p+1,α+21,α+22,…,α+2p+2,…,α+n1,α+n2,…,α+np+n)T
G-=(α-11,α-12,…,α-1p-1,α-21,α-22,…,α-2p-2,…,α-n1,α-n2,…,α-np-n)T
h+e=(h+11e,h+12e,…,h+1p+1e,h+21e,h+22e,…,h+2p+2e,…,h+n1e,h+n2e,…,h+np+ne)T,e=1,2,…,n+m
H+=((h+1)T,(h+2)T,…,(h+n+m)T)T
h-e=(h-11e,h-12e,…,h-1p-1e,h-21e,h-22e,…,h-2p-2e,…,h-n1e,h-n2e,…,h-np-ne)T,e=1,2,…,n+m
H-=((h-1)T,(h-2)T,…,(h-n+m)T)T
則系統(1)可表示為
dXidt=fi(X,q),t∈[0,T],i=1,2,…,nXi(0)=Xi0 (2)
系統(2)具有以下性質:
性質1fi(X,q)(i=1,2,…,n)在[0,T]上連續可微,且fi關于q∈Qad連續。
性質2fi(X,q)(i=1,2,…,n)滿足線性增長條件,即存在β,γgt;0,使得
‖f1(X,q),f2(X,q),…,fn(X,q)‖≤β‖X‖+γ
性質3對于q∈Qad,系統(2)的解X(t;q)存在且唯一,且X(t;q)關于q連續。
對任意的X0=(X10,X20,…,Xn0)∈Rn+,定義系統(2)的解集S(X0)為
S(X0):={X(t;q)∈C([0,T];Rn+)|X(t;q)為系統(2)對應q∈Qad的解}
由性質1和性質3知,從q∈Qad到X(t;q)∈S(X0)的映射是連續的,由此可得到如下性質:
性質4解集S(X0)是C([0,T];Rn+)中的緊集。
3參數估計問題
設XEi(ts)(i=1,2,…,n)表示Xi在t=ts(s=1,2,…,M)時刻的實驗值,XEimax表示Xi實驗值的最大值,Xi(ts)表示Xi在t=ts時刻的模型計算值,Ei(ts)表示Xi在t=ts時刻的實驗斜率值,i(ts)表示Xi在t=ts時刻的計算斜率值,Eimax表示Xi的實驗斜率的最大值。
為了估計系統(2)的模型參數值,以濃度誤差準則和斜率誤差準則之和為極小化目標,建立如下參數估計優化模型:
minF=1nM∑ni=1∑Ms=1(XEi(ts)-Xi(ts))2(XEimax)2+1nM∑ni=1∑Ms=1(Ei(ts)-i(ts))2(Eimax)2
s.t.dXidt=fi(X,q),t∈[0,T],i=1,2,…,n(3)
X(0)=X0
q∈Qad
參數估計優化問題(3)具有以下性質:
性質5GMA-系統的參數估計優化問題(3)存在最優解q∈Qad。
4參數估計問題的求解方法
由于參數估計優化問題(3)的約束條件含有微分方程,所以不能直接對其進行求解,通常的做法是先對微分方程進行離散化,然后將原問題轉化為非線性規劃問題。本文利用修正配置離散化公式[16]將式(3)中的微分方程轉化為如下代數方程:
Xi(ts)XEi(ts-1)+0.5λs(fi(XE(ts),q)+fi(XE(ts-1),q)),s=1,2,…,M,i=1,2,…,n(4)
其中:XE=(XE1,XE2,…,XEn)T;λs=ts-ts-1,0=t0lt;t1lt;t2lt;…lt;tM-1lt;tM=T。于是,參數優化問題(3)可以轉化為如下非線性規劃問題:
minF=1nM∑ni=1∑Ms=1(XEi(ts)-Xi(ts))2(XEimax)2+1nM∑ni=1∑Ms=1(Ei(ts)-i(ts))2(Eimax)2
s.t.Xi(ts)XEi(ts-1)+0.5λs(fi(XE(ts),q)+fi(XE(ts-1),q)),s=1,2,…,M,i=1,2,…,n,q∈Qad(5)
其中XE(t0)=XE(0)=X0。
非線性規劃問題(5)可進一步轉化為如下只含參數變量q的優化問題:
minF=1nM∑ni=1∑Ms=1(XEi(ts)-XEi(ts-1)-0.5λs(fi(XE(ts),q)+fi(XE(ts-1),q)))2(XEimax)2+
1nM∑ni=1∑Ms=1(Ei(ts)-fi(XE(ts),q))2(Eimax)2(6)
s.t.q∈Qad
綜上所述,本文提出了估計GMA-型生物化學系統模型參數的迭代算法。
算法:
步驟1建立系統(2)的參數估計優化模型(3)。
步驟2應用B樣條方法估計實驗數據的斜率Ei(ts)(s=1,2,…,M,i=1,2,…,n)。
步驟3利用修正配置離散化公式(4)將參數估計優化模型(3)中的微分方程轉換為代數方程,從而將模型(3)轉化為非線性規劃問題(6)。
步驟4給定計算次數v,令迭代次數u=1。
步驟5在第u(u≥1)次迭代,隨機產生初始參數值q(0)∈Qad,應用序列二次規劃算法求解優化問題(6)。令最優解為q(u),目標值為F(u)。
步驟6若u=v,則停止迭代,轉步驟7;否則令u=u+1,轉步驟5。
步驟7計算F(u)=min1≤u≤v{F(u)}。輸出最優解q(u)及其目標值F(u)。
5計算研究
例1考慮如下GMA-型生物化學系統[17]:
dX1dt=α+11Xh+1122Xh+1133Xh+1144-α-11Xh-1111Xh-1122-α-12Xh-1211Xh-1233
dX2dt=α+21Xh+2111Xh+2122-α-21Xh-2122
dX3dt=α+31Xh+3111Xh+3133-α-31Xh-3133(7)
取初值X(0)=(0.5,0.5,1,0.25)T,T=4,λs=0.05,各參數值的真實值[17]見表1。參數估計優化模型為
minF=13M∑3i=1∑Ms=1(XEi(ts)-Xi(ts))2(XEimax)2+13M∑3i=1∑Ms=1(Ei(ts)-i(ts))2(Eimax)2
s.t.dX1dt=α+11Xh+1122Xh+1133Xh+1144-α-11Xh-1111Xh-1122-α-12Xh-1211Xh-1233
dX2dt=α+21Xh+2111Xh+2122-α-21Xh-2122
dX3dt=α+31Xh+3111Xh+3133-α-31Xh-3133
t∈[0,4]
X(0)=(0.5,0.5,1,0.25)T
0≤α+i1≤8,i=1,2,3
0≤α-i1≤8,i=1,2,3
0≤α-12≤8
-2≤h+11e≤1,e=2,3,4
-2≤h+21e≤1,e=1,2
-2≤h+31e≤1,e=1,3
-2≤h-11e≤1,e=1,2
-2≤h-12e≤1,e=1,3
-2≤h-212≤1
-2≤h-313≤1
表1給出了例1的計算結果,相應的最優目標值F為2.02190651×10-7。由表1可知應用本文方法估計出的參數值與真實值比較接近。
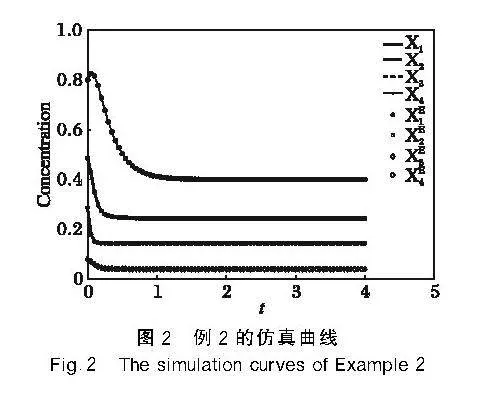
將表1的參數估計值代入到系統(7)中,得到了代謝物濃度隨時間變化的曲線圖(圖1)。從圖1中可以看出,各代謝物濃度的計算值與實驗值基本一致,說明本文方法得到了較好的參數估計結果。
例2考慮如下GMA-型生物化學系統[18]:
dX1dt=α+11Xh+1155-α-11Xh-1111Xh-1166
dX2dt=α+21Xh+2111Xh+2166-α-21Xh-2111Xh-2122Xh-2133Xh-2177-α-22Xh-2222Xh-2233Xh-2244Xh-2288(8)
dX3dt=α+31Xh+3111Xh+3122Xh+3133Xh+3177-α-31Xh-3133Xh-3199
dX4dt=α+41Xh+4122Xh+4133Xh+4144Xh+4188-α-41Xh-4144Xh-411010
取初值X(0)=(0.2858,0.485,0.0786,0.8002,2,2,2,2,2,2)T,T=4,λk=0.05,各參數值的真實值[18]見表2。參數估計優化模型為
minF=14M∑4i=1∑Ms=1(XEi(ts)-Xi(ts))2(XEimax)2+14M∑4i=1∑Ms=1(Ei(ts)-i(ts))2(Eimax)2
s.t.dX1dt=α+11Xh+1155-α-11Xh-1111Xh-1166
dX2dt=α+21Xh+2111Xh+2166-α-21Xh-2111Xh-2122Xh-2133Xh-2177-α-22Xh-2222Xh-2233Xh-2244Xh-2288
dX3dt=α+31Xh+3111Xh+3122Xh+3133Xh+3177-α-31Xh-3133Xh-3199
dX4dt=α+41Xh+4122Xh+4133Xh+4144Xh+4188-α-41Xh-4144Xh-411010
t∈[0,4]
X(0)=(0.2858,0.485,0.0786,0.8002,2,2,2,2,2,2)T
0≤α+i1≤16,i=1,2,3,4
0≤α-i1≤16,i=1,2,3,4
0≤α-22≤16
-2≤h+115≤2
-2≤h+21e≤2,e=1,6
-2≤h+31e≤2,e=1,2,3,7
-2≤h+41e≤2,e=2,3,4,8
-2≤h-11e≤2,e=1,6
0≤h-211≤2
-2≤h-21e≤2,e=2,7
-2≤h-213≤0
0≤h-223≤2
-2≤h-22e≤2,e=2,4,8
-2≤h-31e≤2,e=3,9
-2≤h-41e≤2,e=4,10
表2給出了例2的計算結果,相應的最優目標值F為4.50885464×10-3。由表2可知,應用本文方法估計出的參數值與真實值比較接近。
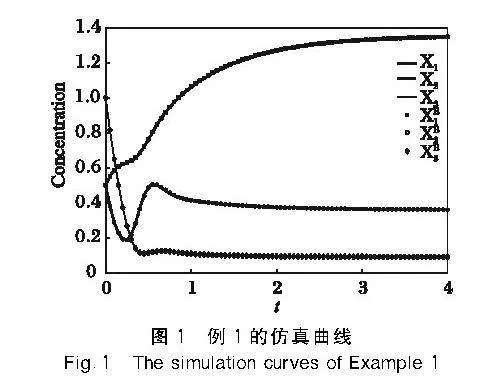
將表2的參數估計值代入到系統(8)中,得到了代謝物濃度隨時間變化的曲線圖(圖2)。從圖2中可以看出,各代謝物濃度的計算值與實驗值基本一致,說明本文方法得到了較好的參數估計結果。
6結語
本文給出了GMA-型生物化學系統的數學模型及其數學性質,構建了一種參數估計優化模型,設計了有效的計算方法求解構建的參數估計優化模型。數值計算與仿真結果表明,本文給出的GMA-型生物化學系統的參數估計方法可以獲得較為精確的模型參數估計結果。
參考文獻:
[1]KRAJCINOVIC D,FONSEKA G U.The continuous damage theory of brittle materials[J].J Appl Mech,1981,48(4):809-824.
LOSKOT P,ATITEY K,MIHAYLOVA L.Comprehensive review of models and methods for inferences in bio-chemical reaction networks [J].Front Genet,2019,10:549.
[2]GARCA-NIETO J,NEBRO A J,ALDANA-MONTES J F.Inference of gene regulatory networks with multi-objective cellular genetic algorithm [J].Comput Biol Chem,2019,80:409-418.
[3]HURTADO S,GARCIA-NIETO J,NAVAS-DELGADO I,et al.Reconstruction of gene regulatory networks with multi-objective particle swarm optimisers [J].Appl Intell,2021,51:1972-1991.
[4]KIMURA S,IDE K,KASHIHARA A.Evolutionary optimization with data collocation for reverse engineering of biological networks [J].Bioinformatics,2005,21(7):1180-1188.
[5]SUN J,GARIBALDI J M,HODGMAN C.Parameter estimation using metaheuristics in systems biology:A comprehensive review [J].IEEE ACM T Comput Bi,2012,9(1):185-202.
[6]XU G,LIU Z.Sequential geometric programming method for parameter estimation of microbial continuous fermentation [J].Int J Chem Eng,2023,2023:8072920.
[7]XU G,LV D,TAN W.A two-stage method for parameter identification of a nonlinear system in a microbial batch process [J].Appl Sci-Basel,2019,9(2):337.
[8]ZHAO Y,XU G.Parameter identification and steady-state optimization of microbial continuous fermentation based on two-stage and interior point methods [J].J Ind Manag Optim,2024,20(10):3048-3071.
[9]TASK K,BANERJEE I.An integer optimization algorithm for robust identification of non-linear gene regulatory networks [J].Bmc Syst Biol,2012,6(1):119.
[10]SARODE K D,KUMAR V R,KULKAMI B D.Inverse problem studies of biochemical systems with structure identification of S-systems by embedding training functions in a genetic algorithm [J].Math Biosci,2016,275:93-106.
[11]KIMURA S,IDE K,KASHIHARA A,et al.Inference of S-system models of genetic networks using a cooperative coevolutionary algorithm [J].Bioinformatics,2005,21(7):1154-1163.
[12]GILL J,CHETTY M,SHATTE A,et al.Combining kinetic orders for efficient S-system modelling of gene regulatory network [J].Biosystems,2022,220:104736.
[13]劉豐.S-型生化系統的參數估計研究 [D].錦州:渤海大學,2016.
[14]吳家琪,徐恭賢.S-型生化系統的參數估計求解方法[J].沈陽大學學報(自然科學版),2021,33(6):516-522.
[15]徐恭賢,邱添,賈府生,等.一類生物系統的參數估計方法及其應用 [J].計算機工程與應用,2020,56(4):163-167.
[16]LIU P,WANG F.Inference of biochemical network models in S-system using multi-objective optimization approach [J].Bioinformatics,2008,24(8):1085-1092.
[17]VOIT E O.Computational analysis of biochemical systems:A practical guide for biochemists and molecular biologists [M].Cambridge:Cambridge University Press,2000.
[18]XU G,Li Y.Steady-state optimization of biochemical systems by bi-level programming [J].Comput Chem Eng,2017,106:286-296.
【責任編輯:溫學兵】
收稿日期:2023-09-06
基金項目:國家自然科學基金資助項目(11101051;62273056);遼寧省教育廳高校基本科研項目(JYTMS20231628)。
作者簡介:
徐恭賢(1976—),男,遼寧莊河人,渤海大學教授,博士。

