基于足底壓力分布的下肢步態識別方法*

顏兵兵，王 強，宋佳寶，殷寶麟，胡春玉

（佳木斯大學 機械工程學院，黑龍江 佳木斯 154007）

0 引言

人與外界環境的交互是多模態的，可以通過視覺、味覺、嗅覺、聽覺和觸覺獲取外界信息，利用大腦對獲取的信息進行處理，用以理解外部世界［1］。針對助力外骨骼機器人，良好的下肢步態感知能力是人與外骨骼機器之間融合度評價的關鍵指標，也是人機共融領域［2］的熱點問題。

楊敏等人［3］利用足底壓力采集裝置對行走、跑步和下蹲3種步態信號進行采集并用于人體步態分析。魏鵬娜等人［4］采集腦電波（electroencephalogram，EEG）信號和表面肌電（surface electromyography，sEMG）信號，采用K 最近鄰（K-nearest neighbor，KNN）算法和核支持向量機（kernel SVM，KSVM）算法進行下肢步態感知。劉薛勤等人［5］采集足底周期性運動步態的壓力數據，利用支持向量機（SVM）對下肢步態數據進行分類，由此感知下肢步態。賈曉輝等人［6］提出了一種基于模型映射和卷積神經網絡（convolutional neural network，CNN）區分人體步態相位的方法，并對不同的步態進行識別，可準確感知人體運動意圖。Ivanov K等人［7］使用帶有傳感器鞋墊來收集59 名戶外行走的運動數據，利用CNN對這些數據進行身份識別，平均識別準確度為93.3%。劉今越等人［8］將壓力傳感器和慣性測量單元（inertial measurement unit，IMU）采集的數據融合為足部運動數據，搭建CNN 識別行走步態相位，平均識別準確率為94.58%。

基于前人研究結果可將下肢步態感知的實質理解為：通過不同的感知方式獲取下肢運動信息，并采用不同的神經網絡方法感知不同的下肢步態。可以看出，下肢步態感知方式可歸納為生物信號感知、慣性感知與足底壓力感知。其中，生物信號sEMG的采集易受外界環境的干擾；慣性傳感器佩戴位置的差異性大，均會降低下肢步態感知的效率與精度。相對于上述2 種感知方式，基于足底壓力感知的步態感知方法具有良好的靈敏度與測量精度。

基于此，本文以足底壓力分布為研究對象，構建足底壓力分布采集裝置，采用多元線性回歸法將足底壓力分布數據轉換為地面反作用力，并基于CNN分類算法進行下肢不同步態的感知。

1 足底壓力分布采集

1.1 足底壓力分布采集裝置

足底壓力分布數據是下肢步態感知的數據基礎，鑒于壓力傳感器的數量大小和位置分布方案會直接影響足底壓力采集裝置的采集性能［9］，本文擬定8 只壓力薄膜傳感器的位置分布方案（如圖1）：在足后跟的內外側分布3個傳感器節點（M3，M4，M5）；在足中部外側安裝2 個傳感器節點（M7，M8）；在足前部安裝3個傳感器節點（M1，M2，M6）。

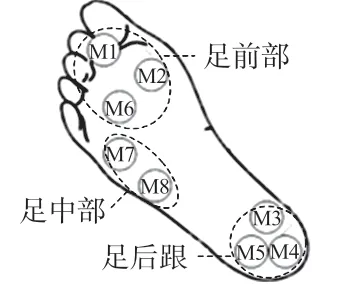
圖1 壓力傳感器的位置分布

本文鑒于成年人站立時的最大足底壓力為（1.28 ±0.33）kg／cm2，運動時的最大足底壓力為（2.96 ±0.66）kg／cm2，且站立與運動時足底與地面最小接觸面積為2 cm2［10］。本文采用柔性薄膜壓力傳感器ZNX—01，設計出一種可穿戴在鞋內的足底壓力采集裝置，裝置實物及其接線圖如圖2所示。

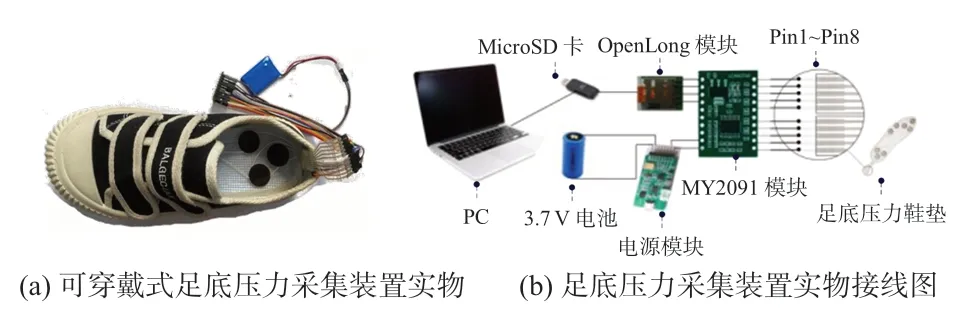
圖2 足底壓力采集裝置

1.2 足底壓力分布采集試驗

邀請身體健康、下肢關節骨骼正常的人員（身高為178 cm，體重為85 kg）為試驗采集對象，開展平地行走（行走速度為1.2 m／s）足底壓力分布數據的采集試驗，試驗結果如圖3所示。其中，M1—M8分別為足底壓力采集裝置中8只壓力傳感器采集的壓力數據。

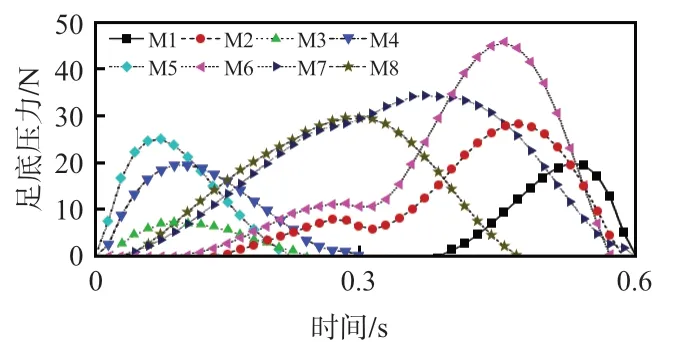
圖3 平地行走時足底各區域壓力曲線

由圖3可知，平地行走一個步態周期內足底壓力變化順序依次為：觸地期時足后跟與地面接觸，足后跟區域（M3，M4，M5）受壓逐漸增大，隨著運動進入承重期，足后跟區壓力逐漸變小，足中前部區域（M2，M6）與地面接觸，足底壓力隨足中前部區域壓力增大而逐漸增大。當運動進入站立期，足后跟區壓力下降，足中部區域（M7，M8）受壓明顯增強。離地期時足前部區域（M1）受力達到峰值，足底其他區域壓力減小或為零。其運動過程與受力順序符合足底生物力學分析結果［10，11］，可用于地面反作用力預測。

2 地面反作用力預測

2.1 地面反作用力預測模型

借助足底壓力采集裝置雖能采集不同步態足底壓力分布數據，但若要感知下肢步態，則需獲取足底整體壓力數據（或稱地面反作用力），而非分布壓力數據。因此，本文基于多元線性回歸法構建足底壓力分布數據X 與地面反作用力Y之間的關系模型

式中 α為回歸系數。若能確定平地行走、平地慢跑和坡路行走3個步態的回歸系數α1，α2和α3；再通過前一節搭建的足底壓力分布采集裝置采集3個步態足底壓力分布數據X1，X2和X3；即可通過式（1）獲得地面反作用力Y。

為獲取回歸系數α，首先借助文獻［12］中經驗公式（見式（2））分別獲取上述3 個步態地面反作用力經驗值

式中 m為人體質量，β為支撐期占比，q為凹陷系數，p為峰值對稱參數，T為步態周期，t為時間；不同步態時，β，q和p取值不同［13，14］；基于式（2）可獲得地面反作用力經驗值

式中 y，y′和y″分別為平地行走、平地慢跑和坡路行走的經驗值；n為采樣樣本數。

然后利用足底壓力分布采集裝置分別采集3個步態足底壓力分布數據X1，X2和X3

式中 x，x′和x″分別為平地行走、平地慢跑和坡路行走足底壓力分布的采樣數據。

最后利用式（5）計算出3 個步態的線性回歸方程的回歸系數

將式（4）和式（5）代入式（1）中，即可獲得平地行走、平地慢跑和坡路行走3個步態的地面反作用力的預測模型

2.2 地面反作用力預測試驗

首先，針對平地行走（1.2 m／s）、平地慢跑（2.2 m／s）和坡路行走（坡度為10.8°，1.2 m／s）3 個不同步態，分別采集試驗者在平坦地面上20 組足底壓力分布數據；其次，將表1設定的參數［13，14］代入式（2）中計算出地面反作用力經驗值；然后，選取10 組足底壓力分布數據進行線性回歸試驗分析，并將調整后擬合度指標（R2）最高的一組確定為足底壓力分布數據；最終，由式（5）求得上述3個步態對應的回歸系數α1，α2和α3

表1 不同步態地面反作用力經驗參數

以此確定該試驗條件下3個步態的地面反作用力預測模型。基于此模型，從3個不同步態的20組數據中選擇另外的10組足底壓力分布數據進行地面反作用力預測獲得預測值Y1，Y2和Y3，并與經驗值進行對比。選取其中一組對比結果，如圖4 所示。可以看出，3 個不同步態地面反作用力的預測值與經驗值基本一致。

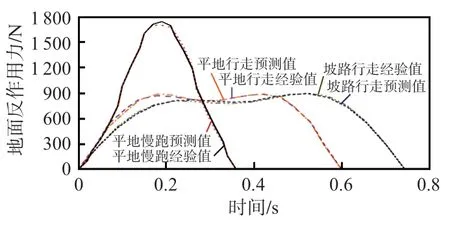
圖4 不同步態地面反作用力預測值與經驗值對比

引入歸一化均方根誤差（normalized root mean square error，NRMSE）作為誤差評價指標，將預測值與經驗值做誤差對比分析，結果如圖5所示。可以看出，3 個步態地面反作用力預測值與經驗值的NRMSE均在4%～10%之間，平均誤差分別為7.4%，7.7%和6.0%，預測結果均在工程應用的接受范圍內［15］，滿足后續步態感知的需求。

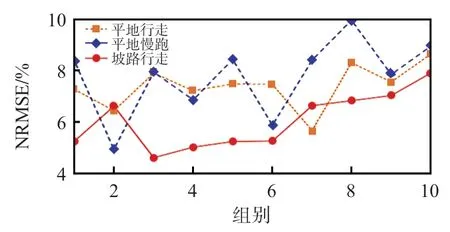
圖5 地面反作用力預測值與試驗值的NRMSE

3 下肢步態感知

3.1 下肢步態感知算法

平地行走、平地慢跑和坡路行走3 個步態的地面反作用力的變化趨勢存在明顯差異，可從上述3 個步態的地面反作用力原始數據中提取包括均值、標準差、均方根和最小值在內的特征值，再采用Mapminmax函數針對上述特征值進行歸一化處理，以便得到用于CNN學習所用的訓練與測試數據，最終獲得下肢不同步態的分類結果，以此實現基于足底壓力分布的下肢步態感知功能，具體流程如圖6所示。

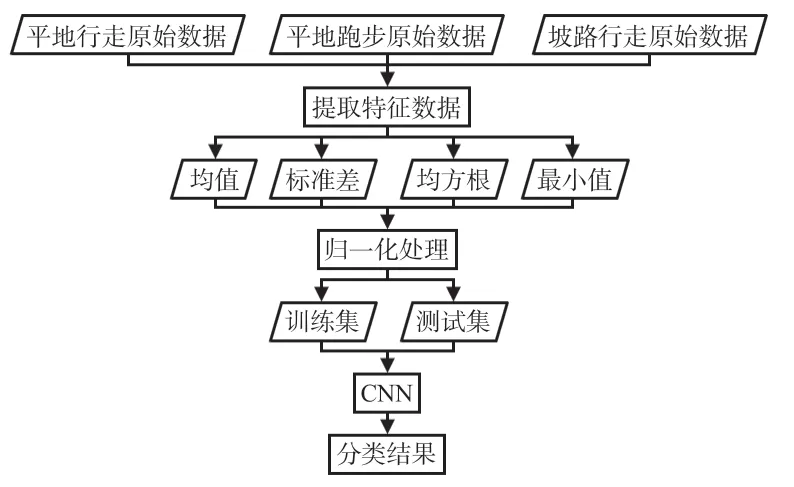
圖6 基于足底壓力分布的下肢步態感知流程

本文搭建的CNN架構（如圖7）由卷積結構和分類器構成，其中卷積結構由2 個卷積（Con1，Con2）層、1 個最大池化（Maxpool）層和2個批歸一化（Norm1，Norm2）層組成，分類器由1個全連接（FC）層和1個SoftMax層組成。

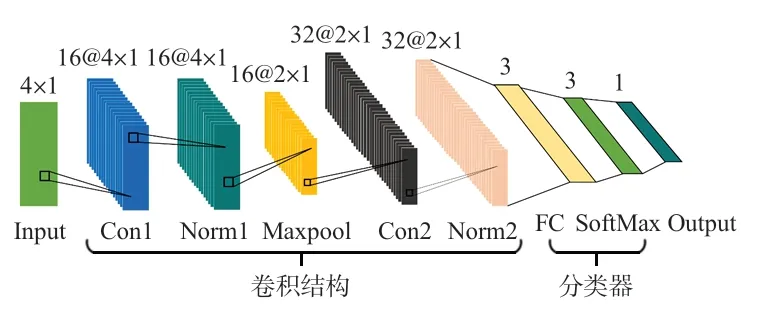
圖7 用于下肢步態感知的CNN架構

首先將歸一化處理后數據樣本作為CNN的輸入（Input），經由卷積結構進行數據特征提取，再經過分類器中的FC層將其映射至樣本標記空間，然后通過SoftMax 層選擇最大預測概率的類別作為分類結果，最終輸出至Output。

3.2 試驗分析

針對平地行走、平地慢跑和坡路行走3 個步態展開足底壓力分布采集試驗，利用地面反作用力預測模型分別獲取上述3個步態的地面反作用力數據，經過提取特征數據與歸一化處理，獲得300 組數據樣本，并將其劃分為CNN所需的訓練集與測試集（見表2）。

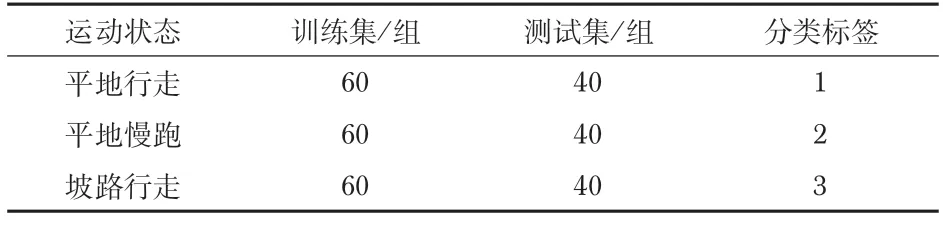
表2 CNN不同步態的訓練集與測試集

訓練過程中，設置學習率為0.001，訓練次數為500，訓練集損失值及準確率的結果如圖8 所示。可以看出，訓練樣本的準確率達到98.95%，而損失值在訓練400 次后趨于穩定，其值為0.05。

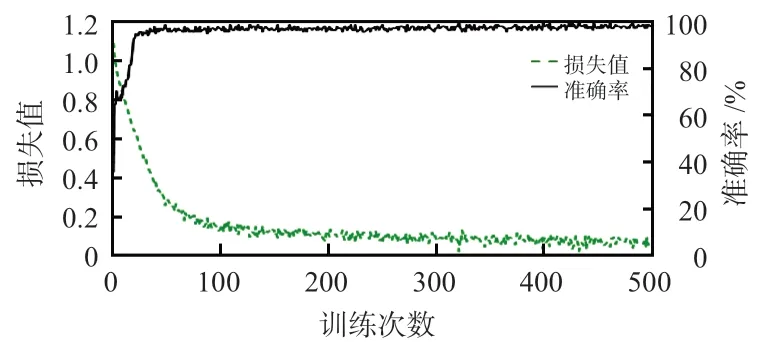
圖8 訓練集的損失值及準確率

將測試集輸入上述訓練得到的CNN模型，進行下肢步態感知的測試試驗，其結果如圖9所示。可以看出，平地行走中40組測試樣本的預測結果完全正確，而平地慢跑和坡路行走中各有1組測試樣本的預測結果有誤。

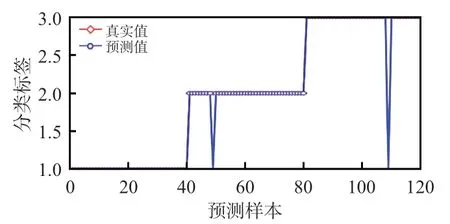
圖9 測試集的測試結果

根據統計測試集各分類標簽的真實值和預測值數量，繪制基于測試集的預測分類混淆圖（如圖10）。可以看出，平地行走、平地慢跑和坡路行走的精確率（Precision）分別為95.2%，100%和100%，召回率（Recall）分別為100%，97.5%和97.5%。

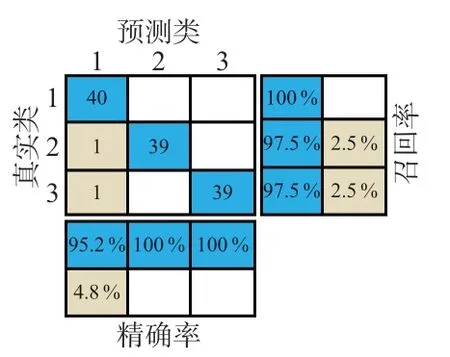
圖10 基于測試集的預測分類混淆圖

引入Fscore指標（如式（8））綜合評價基于測試集的不同步態感知性能

式中 β 為查準率與查全率的調整權重，本文將精確率和召回率視為同等重要，即β ＝1。基于式（8）計算可知平地行走、平地慢跑和坡路行走3 個步態感知的識別率分別為97.5%，98.7%和98.7%，平均識別率達到98.3%，能夠滿足不同步態感知與運動意圖識別的需求。

3.3 對比驗證

為進一步驗證本文所構建的下肢步態感知CNN 的有效性，分別采用SVM 和BP神經網絡替換下肢步態感知流程中的CNN，開展相應的步態感知試驗測試，并進行試驗結果的對比分析。

基于SVM 的步態感知試驗中，選用高斯徑向基函數（radial basis function，RBF）為核函數，采用網格搜索和交叉驗證的方法，在范圍（2－10，210）內尋找最優懲罰參數c和核函數參數g并進行優化，最終獲得懲罰參數c為0.015 6，核函數參數g為1。基于BP神經網絡的步態感知試驗中，隱含層神經元的個數設置為6，輸入層到隱含層之間的傳遞函數設置為tansing，隱含層到輸出層之間的傳遞函數設置為purelin，訓練方法為trainlm，最大迭代次數為500，學習率為0.01，訓練誤差目標為1×10－6。由此可以獲得基于不同識別方法的下肢步態感知識別率的對比結果，如表3所示。

表3 不同識別方法識別率 %

可以看出，本文構建的基于CNN的下肢步態平均識別率達到98.3%，優于SVM和BP神經網絡兩種方法。為諸如下肢助力外骨骼機器人等相關裝置在人機交互技術方面的研究提供了一種可選的方案。

4 結論

本文以足底壓力分布為研究對象，基于足底生物力學分析搭建了一種可穿戴式足底壓力分布采集裝置，并用于平地行走、平地慢跑和坡路行走3 個步態的足底壓力數據采集；基于多元線性回歸法構建出地面反作用力預測模型，準確地將足底壓力分布數據轉換為地面反作用力；基于CNN分類算法實現了下肢不同步態的運動感知，并與SVM和BP 神經網絡進行對比分析，驗證了本文提出的基于CNN分類算法能夠更為準確地感知下肢不同步態。這有助于下肢外骨骼能夠更好地理解用戶意圖，可進一步推動下肢外骨骼在康復、行動輔助和勞動增強等應用領域的技術創新。