Compression and stretching of ring vortex in a bulk nonlinear medium
Xian-Jing Lai(來嫻靜), Xiao-Ou Cai(蔡曉鷗), Ya-Bin Shao(邵雅斌), and Yue-Yue Wang(王悅悅)
1Department of Basic Science,Zhejiang Shuren University,Hangzhou 310015,China
2School of Sciences,Zhejiang A&F University,Hangzhou 311300,China
Keywords: vector optical vortices,dissipative,nonlinear gain
1.Introduction
Dissipative solitons,found abundantly in nature across diverse branches of natural science,emerge as a result of the delicate equilibrium between dispersion, nonlinearity, gain, and loss.They serve as an excellent platform for investigating nonlinear optical dynamics in multiple physical disciplines,including nonlinear optics, fluid dynamics, plasma physics,complex networks, and molecular biology.[1–6]Among dissipative solitons, the dissipative vortex[7–9]is noteworthy.Dissipative vortex structures with nonzero angular momenta have counterparts in nature, such as tornadoes.Vortex solitons self-organize around the zero-strength topological singularity at their center and are characterized by topological charges.[10–14]A dissipative vortex with a fundamental vorticity spontaneously breaks axial symmetry due to modulation instability and can either evolve into a stable rotating ellipsoidal soliton or fragment into filaments.It is generally believed that vortex structures with high topological charges are unstable because modulation instability increases with higher vorticity.Indeed, for higher vorticity, the vortex radius enlarges, intensifying modulation instability and leading to the filamentary disruption of the vortex.
In addition to scalar vortices, many nonlinear systems support vector vortices.The formation of vector vortices is based on the fact that vortices are modes that exist in singlecomponent two-dimensional media.Extending the concept of vortices to two components is both natural and intriguing.Compared to single vortex beams, vector vortex beams offer greater flexibility in beam manipulation,allowing for the creation of more unique beam structures to meet various application requirements.The vector vortex beam, renowned for its vector polarization and helical phase, has been a subject of extensive research due to its potential applications in highresolution imaging, data storage, micromanipulation, molecular orientation research, and 3D beam shaping.In pursuit of these applications,numerous remarkable technologies have been proposed to generate vector vortex beams; however, the creation of novel vector vortex beams remains a significant challenge.[15–18]Despite the availability of numerous numerical investigations, the analytical analysis concerning the formation of vector vortex solitons remains relatively limited.
Research of multicomponent nonlinear systems, involving evolutionary partial differential equations,has gained significant attention in recent years, especially in the fields of optics and atomic physics where multicomponent structures are commonly observed.To thoroughly analyze the propagation of solitons in such systems, researchers often turn to the nonlinear Schr?dinger equation,which effectively captures the simultaneous evolution of multiple classes of solitons.[19–21]Among these equations, the coupled nonlinear Schr?dinger(CNLS) equation stands out, drawing considerable interest in the realms of mathematics and physics.This is due to its ability to support two-component fundamental modes under various optical conditions.[22–26]These equations find widespread application across various branches of physics,including electromagnetics,hydrodynamics,zero-temperature Bose–Einstein condensates, and plasma physics.In particular, within the field of optics, CNLS systems are frequently employed to describe the propagation of light in birefringent fibers.Their versatility in modeling cross-phase and selfphase modulation makes them indispensable tools for understanding complex optical phenomena.
Typically,vector solitons within two-dimensional homogeneous Kerr-type nonlinear media exhibit inherent instability and are susceptible to collapse.However, specific settings,such as spatial modulation nonlinearity,[11,13]can enhance the stability and extend the propagation distance of solitons.In these cases, the fundamental soliton exhibits remarkable stability despite the absence of homogeneity.It is natural to anticipate that the introduction of spatially varying nonlinearity would confer a beneficial influence on the stability of vector systems featuring vortex components.This leads to a natural question: Can spatially varying nonlinearity in a dissipative optical system with nonlinear gain excite vector vortex structures? and if so, how do they evolve? Exploring these questions is both practically significant and the main focus of this study.
In this paper, we present an efficient analytical scheme for the CNLS equation, considering the simultaneous existence of spatial modulation potential energy, nonlinear and linear gain.We delve into the fascinating realm of generating DVVs within this framework, offering a comprehensive exploration of their key attributes.Our analysis delves into how various parameters influence the structural features and energy dynamics of these DVVs.Furthermore, we employ rigorous linear stability analysis to assess the stability of these solitons, providing insights into their robustness.This work addresses several challenges by employing variable separation techniques[27–29]to simplify the problem,resulting in analytical solutions for DVVs in CNLS systems with spatial modulation nonlinearity.The DVVs structures we uncover,expressed in cylindrical coordinates, resemble higher-order beams observed in cylindrical waveguides,such as Laguerre–Gaussian,Whitaker–Gaussian,or Bessel–Gaussian modes,featuring the utilization of Bessel–Gaussian or Bessel–Hyperbolic functions.This comprehensive study allows us to gain a profound understanding of how the effective radius and energy flow of the vortex core evolve with varying parameters.Additionally,our theoretical stability analysis offers valuable insights into the resilience of DVVs under different propagation constants,enhancing our ability to predict their stability.
2.Analytical vector vortices
Presuming that the vector field hasNirrelevant scalar components coupled by nonlinear effects, the system can be expressed as
whereψjare the slowly varying envelopes in the presence of transverse modulationV ≡V(x,y) and propagation distancez.The influence of the functionV(x,y)opposes the impact of nonlinearity,resulting in its attenuation.To find solutions for Eq.(1),we define the complex fieldsψjas



A breakthrough methodology arises from the establishment of a direct mapping between Eqs.(1)and(20),enabling the systematic exploration of numerous precise “soliton islands”amidst an extensive realm of solitary waves.By leveraging a variety ofUforms,the solutions of Eq.(20)can be utilized to derive solutions for Eq.(1).By transforming Eq.(20)into well-known Schr?dinger equations, abundant solutions for Eq.(20) can be generated.Therefore, utilizing Eqs.(2),(6), (15), (23), and (25), a variety of spatially localized stationary exact solutions for Eq.(1)can be derived:
Figures 1 and 2 illustrate typical examples of vector vortex mode compositions with different values ofmandj,clearly demonstrating their vortex characteristics.Vortex solitons with varyingmexhibit phase dislocations, where the phase increases by 2mπaround these dislocations.For a fixedj, the structure expands radially asmincreases.In a similar manner,whenmis held to be constant,the“petals”within the outermost layer progressively expand radially with increasingj.The solution structure changes as its parameters are varied.Figure 3 demonstrates that|ψ1| undergoes a transition from a ring-shaped distribution to a multipole,and then undergoes rotation asdchanges.The solution structure undergoes changes earlier with larger modulation depthp, resulting in ring-shaped distributions whenh<0.5.The phase distribution is similar to Fig.1 and is not drawn to avoid repetition.
Energy balance and energy fluxes hold significant importance in dissipative structures.The Poynting vector serves as a fundamental metric for energy transfer,denoting the density of energy flux or the rate of electromagnetic energy transfer per unit area.In the context of the paraxial approximation utilized in this study,the dimensionless form of the transverse Poynting vector,when averaged over the optical period,is expressed as
whereΦjis given by Eq.(6).By examining the sign of the divergence of the transverse Poynting vector,one can distinguish between energy sinks and energy sources within the transverse section,thereby enabling the separation of domains with contrasting energy characteristics:
Analyzing the curl or vorticity of the Poynting vector allows for the identification of energy flow rotation.Within our particular geometry,the Poynting vector is exclusively composed of a longitudinal component:
where * denotes complex conjugation, andezrepresents the unit vector along thez-axis.The vorticity direction,no matter whether it is parallel or antiparallel toez,depends on the sign of the right-hand side of Eq.(12).Figure 4 displays the radial dependence of energetic characteristics,with both components having the same radial distribution.
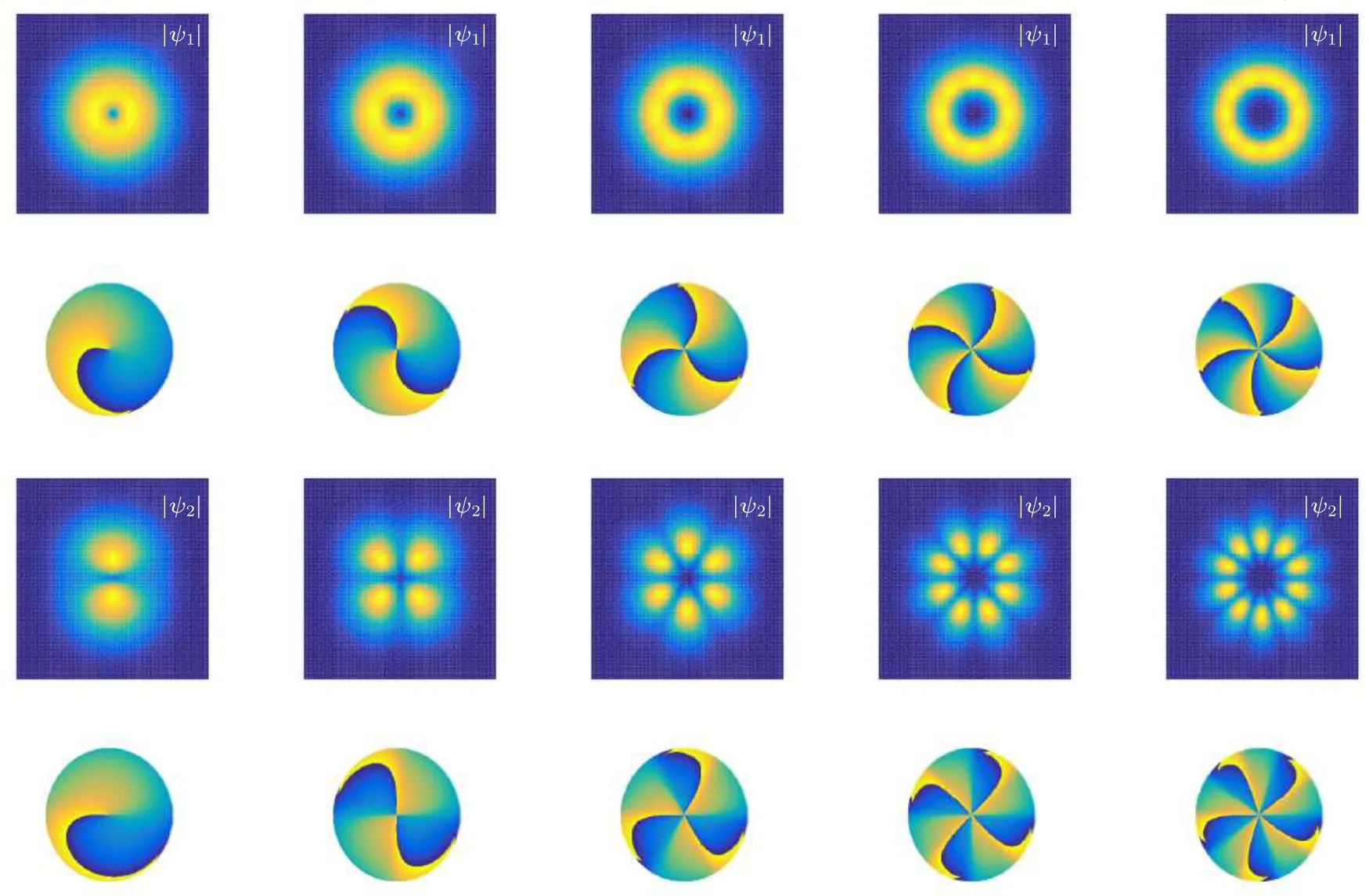
Fig.1.Example of DVVs of Eq.(26) for different topological charge m with j =1, p=0.99, g0 =0, μ =0.12, β =d =0.5,η0=-H=κ1=κ2=1,k=s=0.01,α =-0.2,and a2=1-p2.Intensities and phase profiles are shown at z=0.
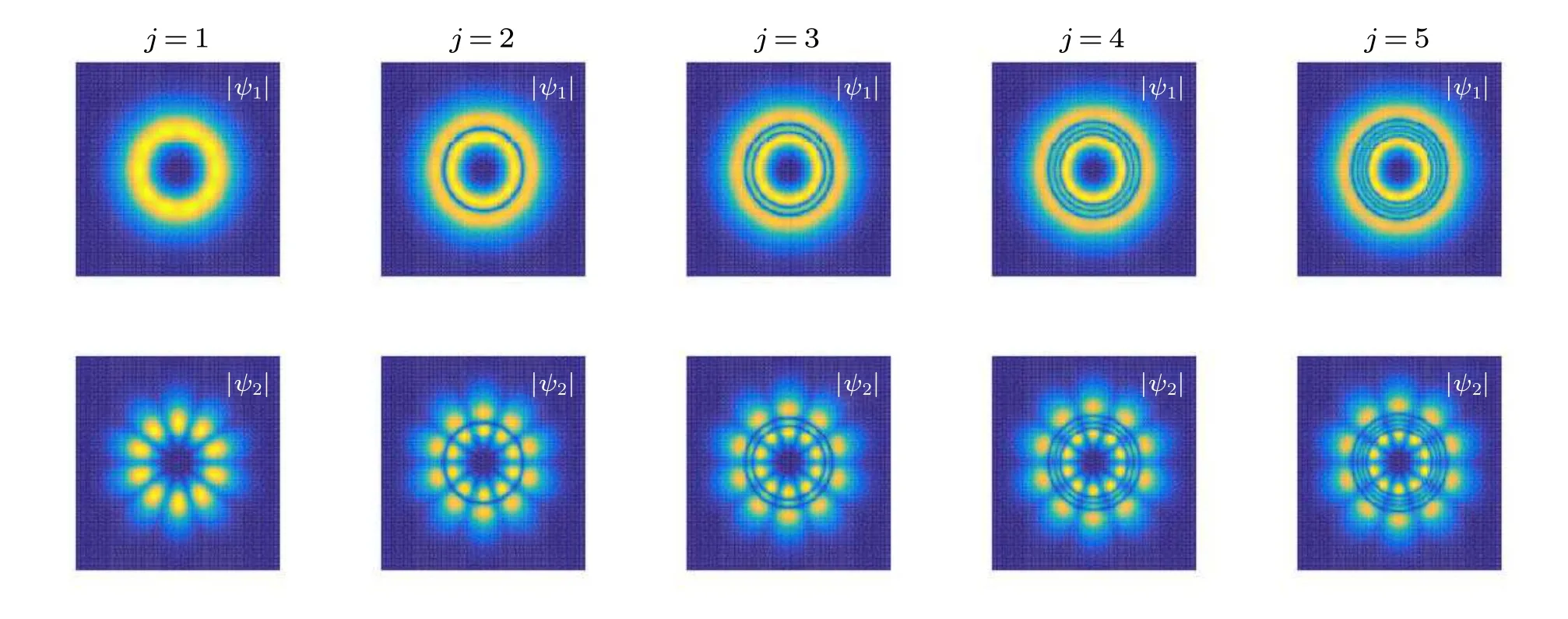
Fig.2.Example of DVVs of Eq.(26)with topological charge j=1,2,3,4,5,m=5.Other relative parameters are the same as those in Fig.1.Intensities are shown at z=0.

Fig.3.Two components of DVVs of Eq.(26)orthogonally arrange in first row and second row,and incoherently superpose to form total quantity|ψ|2=|ψ1|2+|ψ2|2 at z=0 for different h.The parameters are m=1, j=1, p=0.5,s=0.1,d=h/(1-p2),a2=0.5.Other relative parameters are the same as those in Fig.1.
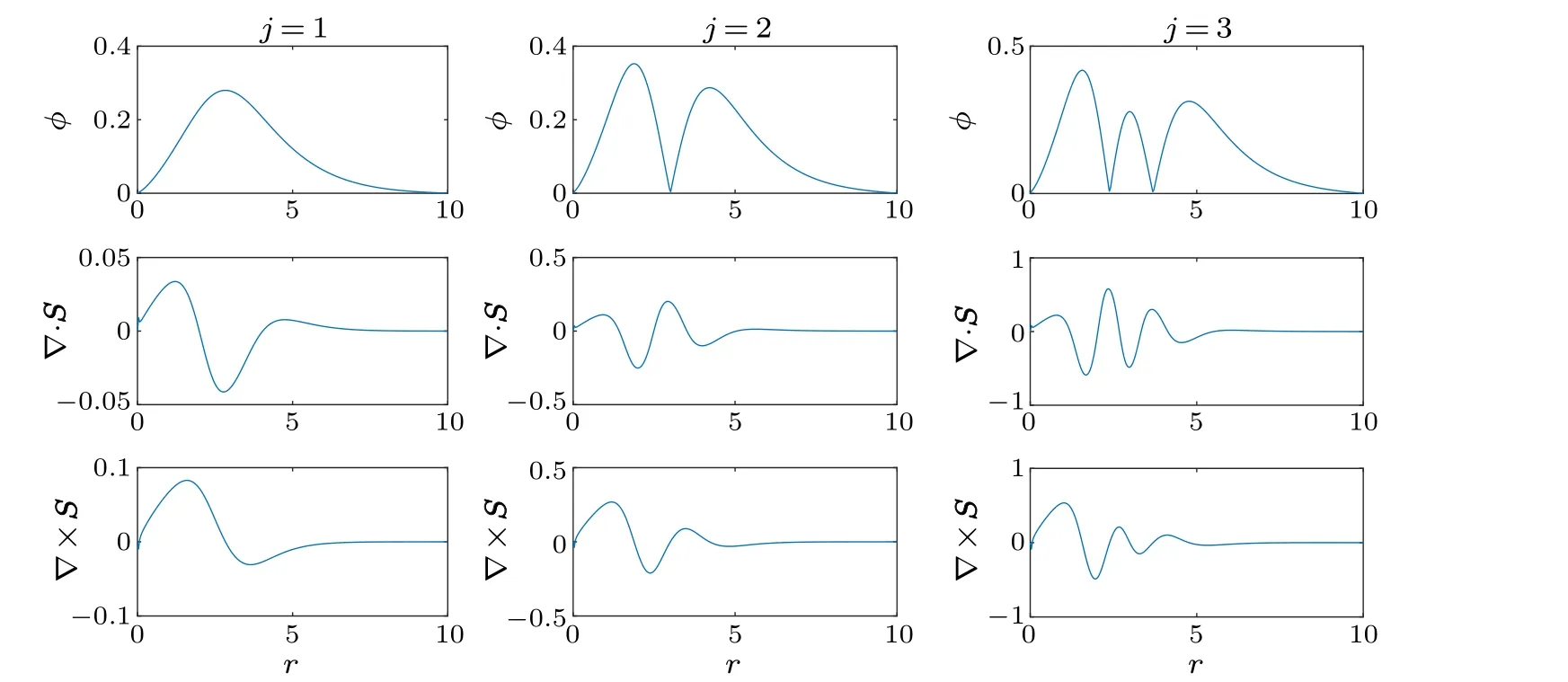
Fig.4.Radial dependencies of energetic characteristics:intensity(top)and divergence(middle)and vorticity(bottom)of the Poynting vector.The parameters are m=2, p=0.5,s=0.5,d=0.2,a2=0.5.Other relative parameters are the same as those in Fig.1.
3.Linear stability analysis of the DVVs
To comprehensively investigate the dynamics of the DVVs featuring diverse topological charges, it is essential to analyze the linear eigenvalue spectra of the corresponding linear system.In this section,we employ linear stability analysis to illustrate and examine the evolution of the above-acquired DVVs.To evaluate the dynamic stability of them, we introduce perturbations to the nonlinear modes using the following expression:
where
and the asterisk symbolizes the complex conjugate,λdenotes the eigenvalue,p(withp=m,m-1,...,1)represents the azimuthal perturbation index,RjandPjare the perturbations satisfying the conditions|Rj|≤Qand|Pj|≤Q,respectively.
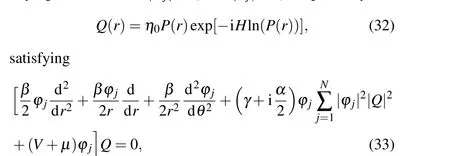

where(·)θstands for derivative ofθ,and*stands for complex conjugation.

Fig.5.Growth rate of DVVs of Eq.(26) with different fixed charges m=1,2,3 for parameters j=1, p=0.6, s=0.6, d =0.68,a2=√0.3.Other relative parameters are the same as those in Fig.1.The value shown near the arrow is the minimum.
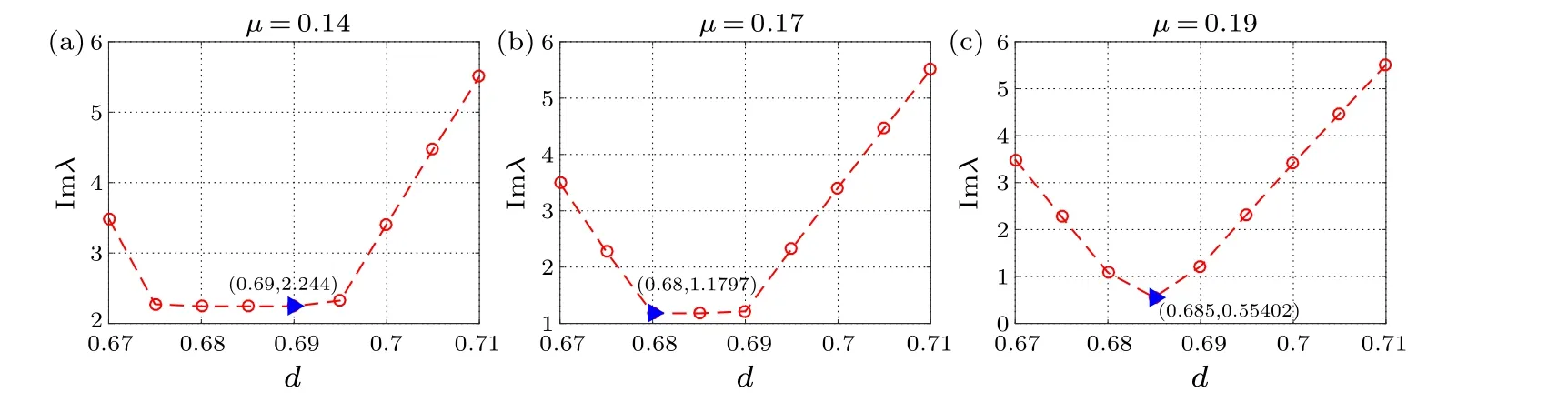
Fig.6.Growth rate of DVVs of Eq.(26)with different propagation constantμ for topological charge m=2.Other relative parameters are the same as those in Fig.5.The value shown near the arrow is the minimum.
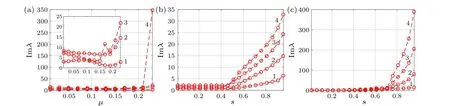
Fig.7.Growth rate of DVVs of Eq.(26)(a)for different index j with m=2,s=0.6, p=0.6,d=0.68,(b)for different topological charge m with j=1, p=0.99, d =3.9, (c) for different index j with m=2, p=0.99, d =3.9 versus related parameters.Other relative parameters are the same as those in Fig.5.
The parameters are pivotal in determining the linear stability of DVVs.We maintain certain parameters while altering others during our analysis.Figures 1–4 illustrate howμ,s, anddinfluence eigenvalue spectra, with the blue triangle representing minimum values.For instance, whens=0.01,p= 0.01, andd= 0.1, the vector vortex adopts a circular shape, resulting in the smallest eigenvalue and the most stable propagation.To minimize the eigenvalue within the given range ofμ, we adjustμto reach a minimum eigenvalue of 1.083 by settingμ=0.19 and fine-tunedto reduce it further to 0.55402 ford=0.685.Figure 1 depicts the relationship between the instability growth rate andμorsfor differentmandjvalues.Largermvalues generally yield greater eigenvalues when other parameters remain constant.The impact ofjon stability depends on the value ofs.For smalls,such ass=0.1,the effect ofjon linear stability is minimal,resulting in similar stability properties for vector solitons with differentjbut the samem.Conversely, with a larges, such ass=0.6, the influence ofjon the eigenvalue becomes more pronounced.It is essential to note that our research assumes a constant nonlinear gain ofα=-0.2.Form ≥1,stable vortex solitons are not found.Vortices with lower power levels tend to collapse progressively,while those with higher topological charges become unstable and transform into lower topological charges at higher power levels.This behavior arises from strong interactions between nonlinear internal modes.However,when nonlinear gain is modulated, the stability of the vector vortex solution significantly improves.Stable vortices with higher topological charges, characterized by multiple phase dislocations, maintain their shapes and phases over long distances without distortion.Further exploration of this aspect awaits future research endeavors.
4.Conclusions
In summary,we propose an efficient approach to analyze the CNLS equation with spatial modulation,nonlinearity,and linear gain.We investigate DVVs and their properties in this nonlinear system.By considering two components, we construct DVVs and study their structure and energy flow influenced by parameters.Additionally,we analyze specific DVV structures to understand the impact of parameter changes on the vortex core.We assess soliton stability using linear stability analysis.Challenges addressed include variable separation,obtaining analytical solutions, and predicting stability based on disturbance growth rates.
Acknowledgement
This work was supported by the National Natural Science Foundation of China(Grant Nos.11705164 and 11874324).
- Chinese Physics B的其它文章
- Quantum synchronization with correlated baths
- Preparing highly entangled states of nanodiamond rotation and NV center spin
- Epidemic threshold influenced by non-pharmaceutical interventions in residential university environments
- Dynamical behavior of memristor-coupled heterogeneous discrete neural networks with synaptic crosstalk
- Dynamics and synchronization in a memristor-coupled discrete heterogeneous neuron network considering noise
- Spatial search weighting information contained in cell velocity distribution

