水下旋翼式平臺近水底擾動定深控制方法研究

宋智斌，黎時宇，戴建生

(1.天津大學(xué) 機(jī)械工程學(xué)院，天津，300354；2.天津大學(xué) 現(xiàn)代機(jī)構(gòu)學(xué)與機(jī)器人學(xué)中心，天津，300354；3.機(jī)構(gòu)理論與裝備設(shè)計教育部重點(diǎn)實(shí)驗(yàn)室，天津，300354；4.南方科技大學(xué) 機(jī)器人研究院，廣東 深圳，518055；5.倫敦國王學(xué)院 機(jī)器人學(xué)中心，英國 倫敦，WC2R 2LS)

隨著水下航行器設(shè)計技術(shù)和控制理論的發(fā)展，水下航行器已能實(shí)現(xiàn)海洋觀測以及近海底操作等任務(wù)，被廣泛應(yīng)用于海洋科學(xué)研究、海洋工程作業(yè)、國防軍事等領(lǐng)域[1]。近年來，隨著海洋工程的深入發(fā)展，人們對水下航行器的控制精度和抗干擾能力的要求逐步提升。

旋翼運(yùn)動方式以其結(jié)構(gòu)簡單、機(jī)動性好、自主懸停等優(yōu)點(diǎn)在無人機(jī)領(lǐng)域得到廣泛應(yīng)用[2]。由于水和空氣之間存在相似性，一些研究人員將旋翼運(yùn)動模式用于新型水下航行器。旋翼式水下機(jī)器人相較于傳統(tǒng)水下航行器，可以實(shí)現(xiàn)定點(diǎn)懸停，適合執(zhí)行小范圍內(nèi)的水下抓取、探索等復(fù)雜任務(wù)。PIERROT等[3]創(chuàng)造性地提出了6旋翼式布局，并在理論上證明了其可行性。RANGANATHAN等[4]提出了一種四旋翼水下機(jī)器人“AQUAD”，并對其控制器進(jìn)行了仿真實(shí)驗(yàn)。邊靖偉等[5-7]開發(fā)了一種新型類四旋翼無人水下航行器(QUUV)，采用滑模控制方法設(shè)計控制器，并在水池中進(jìn)行仿真和實(shí)驗(yàn)驗(yàn)證，同時給出了QUUV的控制分配方法。宋保維等[8-9]基于流體力學(xué)方法，對水下四旋翼的外形進(jìn)行優(yōu)化減阻，為航行器的外形設(shè)計提供了參考。TAN等[10]提出了一種可變形的水上四旋翼飛行器，其旋翼可以在不旋轉(zhuǎn)機(jī)身的情況下變化方向。JI等[11]以低成本水下觀測為目標(biāo)，提出了一種新型動態(tài)水下航行器(NDUV)；對動力學(xué)模型進(jìn)行了分析，并提出了一種模糊PID控制器來控制航行器的下潛深度和姿態(tài)。LI等[12]提出了一種新型跨介質(zhì)吸附仿生機(jī)器人，結(jié)合四旋翼無人機(jī)和仿生鯽魚吸盤，利用自適應(yīng)變形的折疊槳葉在水/空介質(zhì)之間實(shí)現(xiàn)穩(wěn)定、連續(xù)、快速跨越切換。

可以看出，旋翼式水下平臺系統(tǒng)的合理性已經(jīng)得到了初步的理論驗(yàn)證，其穩(wěn)定的近水底懸停性能是水下機(jī)器人系統(tǒng)在執(zhí)行水下抓取、探索、觀測等任務(wù)所需要的關(guān)鍵性能。水下旋翼式平臺在靠近水底工作時，推進(jìn)器所產(chǎn)生的水流會對水底產(chǎn)生一定的沖擊，從而產(chǎn)生未知時變的非線性反沖擊力，給平臺帶來擾動。同時，系統(tǒng)內(nèi)部的參數(shù)不確定性也會影響水下平臺的穩(wěn)定性與控制精度。有效消除水底反沖擊力干擾與參數(shù)不確定共同產(chǎn)生的非匹配不確定性是水下旋翼式平臺順利完成相應(yīng)任務(wù)的前提。然而，針對水下旋翼式平臺在近水底反沖擊力作用下運(yùn)動控制的研究尚未有相關(guān)報道。

現(xiàn)有水下旋翼式機(jī)器人的控制方法包括傳統(tǒng)控制方法即PID控制和先進(jìn)控制方法。BIAN等[6,13]利用滑模控制實(shí)現(xiàn)了水下類四旋翼航行器的運(yùn)動控制，對于模型中有確定界的匹配干擾有較好的控制效果，但對于具有不確定界的干擾則無法滿足控制要求；自適應(yīng)控制[14]適用于不確定干擾邊界為常值的情況，在理想情況下隨時間趨于無窮而漸近收斂，但在實(shí)際應(yīng)用中難以保證其瞬態(tài)性能；模糊控制[11,15]雖然無需數(shù)學(xué)模型，但其規(guī)則和隸屬函數(shù)設(shè)計缺乏系統(tǒng)性；神經(jīng)網(wǎng)絡(luò)控制[16-17]能得到一些理想的結(jié)果，但實(shí)時控制比較耗時，計算量大；任杰[18]利用模型預(yù)測控制實(shí)現(xiàn)了水下四旋翼的定深控制，其能夠處理各類約束條件，但實(shí)時性差，計算復(fù)雜度高，參數(shù)選擇較為困難。

針對以上研究，本文提出一種基于干擾觀測器的魯棒非線性控制器。該控制器采用動態(tài)面控制(dynamic surface control, DSC)處理系統(tǒng)的非線性特性，利用一階低通濾波器對虛擬控制律進(jìn)行濾波，將微分運(yùn)算轉(zhuǎn)換為簡單且易于實(shí)現(xiàn)的代數(shù)運(yùn)算，降低控制算法復(fù)雜性[19-20]，使系統(tǒng)離散化，以便將算法移植到單片機(jī)中；將水底反流沖擊力產(chǎn)生的時變不確定界的非線性干擾和參數(shù)不確定性一同視作未知擾動的一部分，采用擾動補(bǔ)償技術(shù)克服系統(tǒng)內(nèi)外部總擾動，有效地處理近水底任務(wù)所帶來的未知反沖擊力，同時解決系統(tǒng)內(nèi)部的參數(shù)不確定性問題，相比于DSC控制器和串級PID控制，有效地提高了在不確定界干擾下的定深穩(wěn)定性。

本文建立水下旋翼式平臺運(yùn)動學(xué)及動力學(xué)模型，該模型考慮了作用于系統(tǒng)的流體慣性力及流體阻尼力，其精確度更高；將系統(tǒng)內(nèi)部的參數(shù)不確定性視為外部干擾而不是變化的物理參數(shù)，使系統(tǒng)成為非線性時不變系統(tǒng)，這樣，DSC方法就可以處理系統(tǒng)的非線性特性；同時，通過非線性干擾觀測器(nonlinear disturbance observer, NDO)有效地處理系統(tǒng)內(nèi)外部總擾動引起的時變不確定性；通過數(shù)值仿真及樣機(jī)實(shí)驗(yàn)，驗(yàn)證所提出的控制器的有效性和魯棒性。

1 水下旋翼式平臺數(shù)學(xué)模型

水下旋翼式平臺(underwater rotor-type platform, URP)的結(jié)構(gòu)設(shè)計借鑒了四旋翼結(jié)構(gòu)設(shè)計。下面根據(jù)ANTONELLI[21]提出的水下航行器建模理論并結(jié)合牛頓-歐拉方法建立URP的運(yùn)動學(xué)模型和動力學(xué)模型。

水下旋翼式平臺示意圖如圖1所示。M1、M2、M3和M4這4個推進(jìn)器的布置采用X形結(jié)構(gòu)，推進(jìn)器M1和推進(jìn)器M3呈順時針旋轉(zhuǎn)，而推進(jìn)器M2和推進(jìn)器M4呈逆時針旋轉(zhuǎn)。平臺的運(yùn)動由4個可控的自由度(橫搖、縱搖、艏搖和垂蕩)組成。URP的姿態(tài)和運(yùn)動可以通過調(diào)整每個推進(jìn)器的旋轉(zhuǎn)速度來控制。

圖1 水下旋翼式平臺示意圖Fig.1 Schematic diagram of URP

為了便于水動力分析，引入2個參考坐標(biāo)系即慣性坐標(biāo)系Ixyz和運(yùn)動坐標(biāo)系Bxyz。水下旋翼式平臺的運(yùn)動學(xué)方程可表示為

其中，η1=[x,y,z]T和η2=[?,θ,ψ]T分別表示URP在慣性坐標(biāo)系下的位置向量和旋轉(zhuǎn)姿態(tài)角向量，?、θ、ψ分別為橫搖角、縱搖角、艏搖角=和分別表示η1的一階導(dǎo)數(shù)和二階導(dǎo)數(shù)；和分別表示η2的一階導(dǎo)數(shù)和二階導(dǎo)數(shù)；v1=[u,v,w]T表示URP在運(yùn)動坐標(biāo)系下x、y、z方向的線速度；v2=[p,q,r]T表示URP在運(yùn)動坐標(biāo)系下繞x軸、y軸、z軸旋轉(zhuǎn)的角速度；和分別表示v1和v2的一階導(dǎo)數(shù)。

RIB和J(η2)分別表示運(yùn)動坐標(biāo)系到慣性坐標(biāo)系的旋轉(zhuǎn)矩陣和角速度的雅可比變換矩陣，其表達(dá)式如下：

為了給控制器設(shè)計一個準(zhǔn)確和合適的數(shù)學(xué)模型，對URP系統(tǒng)進(jìn)行以下假設(shè)：

1) URP是一種剛體，無內(nèi)部作用力和形變；

2) URP的重心與運(yùn)動坐標(biāo)系的原點(diǎn)重合；

3) 根據(jù)實(shí)際運(yùn)動情況，要求?和θ滿足|?|<π/2和|θ|<π/2。

根據(jù)牛頓第二定律，水下航行器的6-DOF標(biāo)準(zhǔn)模型的矩陣形式可以用下式描述：

其中，v=[v1T,v2T]T；M為慣性矩陣；C為科氏力系數(shù)矩陣；D為阻尼力系數(shù)矩陣；g(η)為恢復(fù)力矩陣；向量τ為推進(jìn)器產(chǎn)生的力/力矩。

慣性矩陣M由剛體質(zhì)量矩陣MRB和附加質(zhì)量矩陣MA組成，可表示為

其中：m為平臺的質(zhì)量；Ic=diag{Ix,Iy,Iz}；Ix、Iy、Iz是x、y和z方向的轉(zhuǎn)動慣量。

同樣地，科氏力系數(shù)矩陣C(v)由剛體科氏力矩陣CRB和附加科氏力矩陣CA組成，可表示為

阻尼力系數(shù)矩陣可表示為

其中，Xu、Yv、Zw、Kp、Mq和Nr為線性流體動力項(xiàng)。

恢復(fù)力[22]由平臺所受重力(G=mg)和浮力(W)的合力/力矩組成，其中，g為重力加速度。根據(jù)假設(shè)2)可得，重心坐標(biāo)為[0, 0, 0]，浮力中心坐標(biāo)為[0, 0,zB]，因此，可以得到恢復(fù)力g(η)為

URP所受力/力矩是由4個推進(jìn)器提供的。4個推進(jìn)器的速度為ωi(i=1,2,3,4)，可得URP的總升力和力矩為

其中：cT和cQ分別為推力系數(shù)和反扭矩系數(shù)；L為推進(jìn)器到運(yùn)動坐標(biāo)系原點(diǎn)的距離；U1為運(yùn)動坐標(biāo)系下z方向推進(jìn)器所輸入的力；U2、U3和U4分別為x、y、z方向推進(jìn)器所輸入的力矩。輸入的力/力矩向量可表示為

慣性坐標(biāo)系下的動力學(xué)模型反映了系統(tǒng)產(chǎn)生的力和以慣性坐標(biāo)系為度量的運(yùn)動狀態(tài)之間的關(guān)系，適用于平臺的空間位置控制。因此，可以采用慣性坐標(biāo)系下的位置動力學(xué)方程，以便于設(shè)計控制器。而物體的旋轉(zhuǎn)運(yùn)動在慣性坐標(biāo)系下會更加難以描述，因此，采用運(yùn)動坐標(biāo)系下的姿態(tài)動力學(xué)方程。將式(7)、(9)、(10)、(11)、(12)、(14)代入式(4)可以得到新的動力學(xué)模型：

2 控制器設(shè)計

本文提出一種基于干擾觀測器的動態(tài)面控制器(DSC-NDO)。URP具有4個可控自由度，系統(tǒng)水平方向的運(yùn)動是通過姿態(tài)變化產(chǎn)生水平分力來實(shí)現(xiàn)的，因此，本節(jié)選取3個姿態(tài)通道和深度通道組成的子系統(tǒng)進(jìn)行控制器設(shè)計。

URP在靠近水底工作時，其姿態(tài)角的穩(wěn)定及其深度控制是完成任務(wù)的保障。然而，由于水下系統(tǒng)復(fù)雜的動力學(xué)特性，如固有的非線性和時變特性等，會產(chǎn)生系統(tǒng)內(nèi)部的不確定性，進(jìn)而影響整個系統(tǒng)的穩(wěn)定性與控制精度。本節(jié)采用動態(tài)面控制(DSC)跟蹤各通道的期望信號。由于加入擾動后，很難保證姿態(tài)控制的穩(wěn)定性以及擾動下的零誤差，因此，引入干擾觀測器(NDO)對擾動進(jìn)行估計，并通過輸入加以補(bǔ)償。

以姿態(tài)通道為例，將系統(tǒng)內(nèi)部模型參數(shù)的不確定性與位置通道對該通道的影響當(dāng)作內(nèi)部擾動，與環(huán)境擾動一同視為該通道的總擾動。設(shè)計干擾觀測器(NDO)實(shí)時估計擾動量進(jìn)而補(bǔ)償控制器，以保證在不確定擾動條件下系統(tǒng)的穩(wěn)定性；同時，使用動態(tài)面控制(DSC)處理系統(tǒng)的非線性特性。所提出的基于干擾觀測器的動態(tài)面控制器(DSCNDO)的控制策略如圖2所示。通過4個通道的給定期望量和反饋量得到由DSC-NDO產(chǎn)生的虛擬控制量U1、U2、U3和U4，轉(zhuǎn)換后得到4個推進(jìn)器的控制量，從而實(shí)現(xiàn)系統(tǒng)的控制。

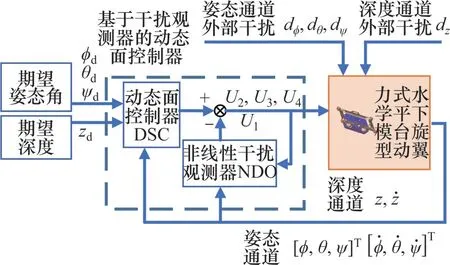
圖2 基于DSC-NDO的控制策略Fig.2 Control strategy based on DSC-NDO

2.1 干擾觀測器設(shè)計

在水下運(yùn)行過程中，水下旋翼式平臺的橫搖角?和縱搖角θ較小，故可對URP的運(yùn)動學(xué)方程進(jìn)行簡化，得到如下關(guān)系式：

實(shí)際應(yīng)用中的擾動隨時間變化，可用非線性項(xiàng)d=(d?,dθ,dψ)T和dz分別表示姿態(tài)通道的干擾項(xiàng)和深度通道的干擾項(xiàng)。以姿態(tài)通道為例，令結(jié)合式(15)，可將系統(tǒng)動力學(xué)方程改寫為

其中：ξ1=[x1,x3,x5]T；=ξ2=[x2,x4,x6]T；g=diag{g1,g2,g3}；Uattitude=[U2,U3,U4]T；f=[f1(x,t),f2(x,t),f3(x,t)]T；Kpx2-z0Wcosx3sinx1；f2(x,t)=h2(x,t)?g2；g2=

針對系統(tǒng)的綜合擾動，構(gòu)造對擾動d的非線性干擾觀測器NDO進(jìn)行觀測補(bǔ)償[23-24]，其形式如下：

定義非線性干擾觀測器的觀測誤差為

由于干擾項(xiàng)d是未知的，在沒有先驗(yàn)知識的條件下，當(dāng)d相較于控制系統(tǒng)的動態(tài)特性變化緩慢時，即認(rèn)為=03×1，根據(jù)式(20)可得：

定義Lyapunov函數(shù)Vd=，對其求導(dǎo)可得

為保證干擾觀測器的觀測誤差收斂，需要選擇合適的L(x)。取L(x)=diag{c1,c2,c3}，其中ci(i=1,2,3)為正常數(shù)，設(shè)計非線性函數(shù)p(x)=L(x)ξ2。

由Lyapunov穩(wěn)定性判據(jù)可知，干擾觀測器是漸近穩(wěn)定的，最終可以收斂到0，且觀測器的指數(shù)收斂速度可通過改變L(x)進(jìn)行調(diào)整。

深度通道參數(shù)設(shè)計如下：

其中，c4為正常數(shù)；Γz為深度通道非線性觀測器的內(nèi)部狀態(tài)參數(shù)。

2.2 基于干擾觀測器的動態(tài)面控制器設(shè)計

基于2.1節(jié)改寫的動力學(xué)方程，定義誤差變量e1為

其中：ξ1d=[x1d,x3d,x5d]T；x1d、x3d、x5d為姿態(tài)通道期望量；和分別表示ξ1d的一階導(dǎo)數(shù)和二階導(dǎo)數(shù)。

構(gòu)建虛擬控制量Ωd：

其中：K1=diag{k11,k12,k13}；k1i>0(i=1,2,3)，為待設(shè)計參數(shù)。

為減少控制器的計算量，引入一階低通濾波器：

其中，為的一階導(dǎo)數(shù)；T1=diag{τ11,τ12,τ13}；τ1i>0(i=1,2,3)，為待設(shè)計時間常數(shù)。

定義一階濾波誤差γ1為

虛擬誤差e2為

設(shè)計合適的控制輸入：

其中：K2=diag{k21,k22,k23}；k2i>0(i=1,2,3)，為待設(shè)計參數(shù)。

對于深度通道，同樣定義誤差變量e1z=z-zd，其中，zd為深度通道的期望深度。

下面對系統(tǒng)的穩(wěn)定性進(jìn)行證明。

引理1給定任何實(shí)數(shù)向量x,y?R3，以下關(guān)系始終成立：

證明通過0≤(x±y)2可得到式(31)。

以姿態(tài)通道閉環(huán)系統(tǒng)為例，定義Lyapunov函數(shù)如下：

對式(32)求導(dǎo)可得：

將式(26)、(27)和(29)代入式(33)可得

由2.1節(jié)可知，干擾觀測器的觀測誤差可以在有限時間T內(nèi)收斂到零，即d=，則式(34)可簡化為

結(jié)合式(27)，對γ1求導(dǎo)可得

將式(36)代入式(35)可得

根據(jù)引理1和Young不等式可知

其中，ε是任意小的常數(shù)，且ε>0。

考慮到虛擬控制信號Ωd的導(dǎo)數(shù)是有界的，即其中，B1為非負(fù)連續(xù)連續(xù)函數(shù)，定義輔助變量：

式中：i=1,2,3。

對式(38)進(jìn)一步處理可得：

引入緊集Ω1和Ω2：

其中：χ為足夠大的正數(shù)；p1≥V1(0)，為正常數(shù)。故此時Ω1×Ω2也是緊集，由此可知，在V1≤p1成立時，B1在Ω1×Ω2上存在最大值M1。

按照如下條件設(shè)計控制參數(shù):

其中：α>2p1/ε，為常數(shù)。

在Ω2的邊界，V1=p1，則≤-αp1+ε/2<0，因此，V1≤p1是一個不變集，即在全局內(nèi)V1(0)≤p1的條件下，V1(t)≤p1。

對式(43)兩端進(jìn)行積分可得

由式(44)可知V1(t)是有界的，故存在某一有限時間t>0，使得結(jié)合式(33)可知通過合理調(diào)整參數(shù)，在保證系統(tǒng)穩(wěn)定性的同時，能夠使跟蹤誤差收斂到任意小。由此可證，姿態(tài)閉環(huán)系統(tǒng)的所有信號都是半全局一致且最終有界的。同理可對深度閉環(huán)系統(tǒng)穩(wěn)定性進(jìn)行證明。

綜上，結(jié)合非線性干擾觀測器觀測得到的干擾估計值可知，姿態(tài)通道的輸入Uattitude為

同理可得深度通道的輸入為

3 數(shù)值仿真及結(jié)果分析

為了驗(yàn)證本文所提出控制策略的優(yōu)越性與有效性，采用MATLAB/Simulink進(jìn)行數(shù)值仿真。此外，為了模擬實(shí)際情況中水底反流對平臺的隨機(jī)擾動，如水中漩渦、摩擦流等未知干擾，驗(yàn)證干擾觀測器對擾動控制的有效性，在動力學(xué)方程中添加高斯分布的白噪聲隨機(jī)擾動，同時加入模型參數(shù)不確定性，在復(fù)合擾動的條件下將其控制效果與動態(tài)面控制器(DSC)和串級PID控制器的控制效果進(jìn)行對比，測試其期望指令的跟蹤能力。在0～30 s對系統(tǒng)姿態(tài)通道添加平均幅值為7.5 N·m、采樣頻率為5 Hz的隨機(jī)擾動；在深度通道添加平均幅值為10 N、采樣頻率為5 Hz的隨機(jī)擾動；同時設(shè)計模型參數(shù)不確定度為20%，即相應(yīng)模型參數(shù)變?yōu)樵瓉淼?0%。水下旋翼式平臺模型參數(shù)和控制器設(shè)計參數(shù)分別如表1和表2所示。其中，串級PID控制器外環(huán)采用角度反饋PID閉環(huán)控制，內(nèi)環(huán)采用角速度增穩(wěn)反饋PID控制。DSC控制器設(shè)計如式(47)所示，即未考慮擾動補(bǔ)償項(xiàng)。

表1 水下旋翼式平臺模型參數(shù)Table 1 Parameters of URP model

表2 控制器參數(shù)Table 2 Parameters of controller

水下旋翼式平臺的初始狀態(tài)值為[x,y,z]T=[0,0,0]Tm，[?,θ,ψ]T=[0,0,0]Trad。在工程中，階躍信號會使系統(tǒng)面臨較為嚴(yán)峻的工作狀態(tài)，同時又符合許多系統(tǒng)的實(shí)際工作情況，所以，常常選用階躍信號來考察系統(tǒng)的動態(tài)性能。如果系統(tǒng)在階躍輸入下的動態(tài)性能指標(biāo)能夠符合要求，那么系統(tǒng)在其他形式輸入下的動態(tài)性能通常也能符合要求。設(shè)計水下旋翼式平臺的姿態(tài)與深度通道參考期望值信號如下：

在串級PID控制器下、動態(tài)面控制器(DSC)、基于干擾觀測器的動態(tài)面控制器(DSC-NDO)下不同通道的響應(yīng)曲線分別如圖3～6所示。在隨機(jī)干擾和參數(shù)不確定的條件下，串級PID、DSC、DSCNDO均保持在期望信號附近。在隨機(jī)干擾的條件下，通過干擾觀測器對擾動進(jìn)行補(bǔ)償后，DSCNDO控制器使得姿態(tài)通道與深度通道能夠快速地達(dá)到期望值，同時具有較小的超調(diào)量。

圖3 橫搖通道響應(yīng)曲線Fig.3 Roll channel response curves

圖4 縱搖通道響應(yīng)曲線Fig.4 Pitch channel response curves

圖5 艏搖通道響應(yīng)曲線Fig.5 Yaw channel response curves

圖6 深度通道響應(yīng)曲線Fig.6 Depth channel response curves

對圖3～6中狀態(tài)量的穩(wěn)態(tài)過程進(jìn)行定量分析。假設(shè)當(dāng)狀態(tài)量到達(dá)期望值并保持在誤差帶內(nèi)振蕩時系統(tǒng)進(jìn)入穩(wěn)態(tài)，分別對圖中各個狀態(tài)量進(jìn)入穩(wěn)態(tài)后的均方根誤差σ和最大誤差emax進(jìn)行計算。

表3和表4所示分別為DSC-NDO控制器、DSC控制器、串級PID控制器下各參數(shù)均方根誤差和最大誤差的對比。由表3和表4可見，URP在DSC-NDO控制器下?、θ、ψ這3個姿態(tài)通道和深度通道z的均方根誤差和最大誤差均比DSC控制器和串級PID控制器的小，能在干擾下高精度地實(shí)現(xiàn)姿態(tài)跟蹤及定深控制。

表3 3種不同控制器均方根誤差對比Table 3 Comparison of the RMSE of three different controllers

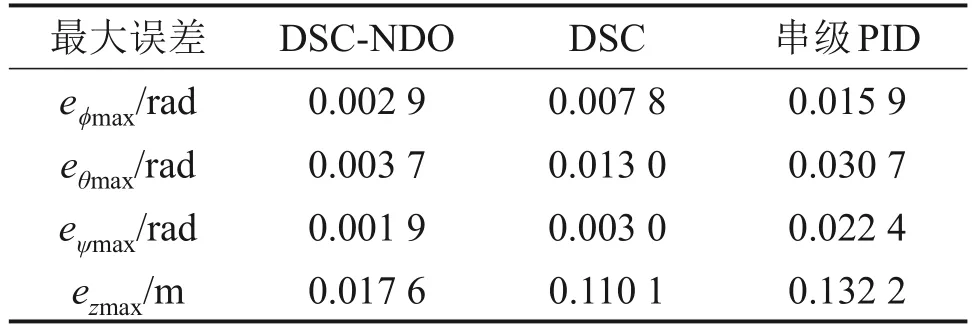
表4 3種不同控制器最大誤差對比Table 4 Comparison of the maximum error of three different controllers

以橫搖通道為例，姿態(tài)通道中深度通道和橫搖通道擾動觀測器的觀測值見圖7，所設(shè)計擾動包括隨機(jī)白噪聲擾動和參數(shù)不確定性。從圖7可以看出復(fù)合擾動估計與真實(shí)總擾動幾乎一致，驗(yàn)證了所設(shè)計觀測器能較好地估計未知的內(nèi)外部擾動。

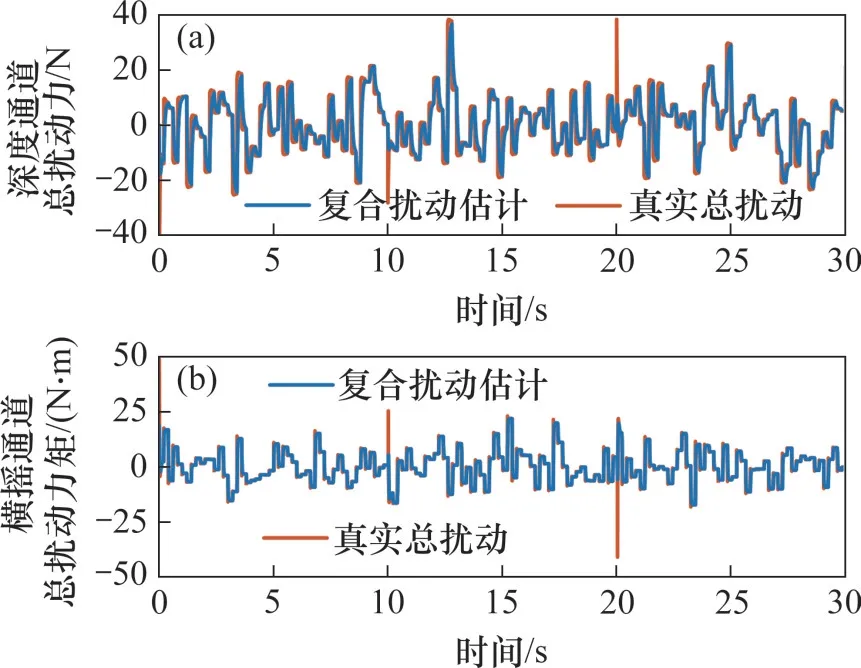
圖7 復(fù)合擾動觀測曲線Fig.7 Composite disturbance observation curve

通過上述仿真分析可見，DSC-NDO可以有效解決外部的高頻非線性干擾和參數(shù)不確定的問題，證明了所設(shè)計的控制策略對具有快速時變特性的隨機(jī)干擾具有有效性和魯棒性。

4 實(shí)驗(yàn)與分析

為了驗(yàn)證本文設(shè)計的基于干擾觀測器的動態(tài)面控制器(DSC-NDO)對水下旋翼式平臺系統(tǒng)的實(shí)際控制效果，采用自主開發(fā)的水下旋翼式平臺進(jìn)行近水底定深懸停實(shí)驗(yàn)。

實(shí)驗(yàn)平臺的電氣系統(tǒng)簡圖如圖8所示。水下旋翼式平臺控制系統(tǒng)采用STM32控制器作為主控制器，同時集成一系列獨(dú)立傳感器，包括慣性測量單元(IMU)和深度傳感器(MS5837)，其中，IMU姿態(tài)角的動態(tài)精度為0.1°，深度傳感器精度為1 cm；遠(yuǎn)程通信控制鏈路通過控制手柄和小型2.4 GHz SBus接收器建立，由于電磁波在水中有損耗，信號在水中會很快完全耗散，所以，接收器被封裝在漂浮在水面上的小型防水盒中，以便于接收信號，其電纜通過防水電纜穿入內(nèi)部連接至控制系統(tǒng)；控制器將傳感器數(shù)據(jù)實(shí)時傳輸?shù)絇C端上位機(jī)中與操作人員通信。整個電氣系統(tǒng)都被封裝在亞克力圓柱中以保證水密性，兩側(cè)通過密封法蘭密封，在其側(cè)面有2個O形環(huán)密封，在其端面有O形環(huán)密封使得外殼完全防水。

圖8 實(shí)驗(yàn)平臺電氣系統(tǒng)簡圖Fig.8 Schematic diagram of electrical system of experimental platform

推進(jìn)系統(tǒng)主要包括4個推進(jìn)旋翼，其中電調(diào)(electronic speed controllers, ESC)用于控制電機(jī)速度。圖9所示為推進(jìn)器靜態(tài)特性曲線。整個推進(jìn)器暴露在水中，采用開放式防水。同時為了獲得良好的散熱條件，ESC安裝在防水密封艙外，并采用導(dǎo)熱性能良好的環(huán)氧樹脂密封，以減小密封艙的空間。

圖9 推進(jìn)器靜態(tài)特性曲線Fig.9 The statics characteristic curves of the thrusters

在自行搭建的水池中進(jìn)行測試，水深約為1.2 m，將水下旋翼式平臺分別在距水底0.3 m處(水深0.9 m)及0.8 m處(水深0.4 m)進(jìn)行水下定深實(shí)驗(yàn)，設(shè)置?、θ、ψ的期望值為0°，定深過程中平臺的姿態(tài)角度信息和深度信息通過數(shù)據(jù)傳輸保存在PC端。分別采用DSC控制器、DSC-NDO控制器和串級PID測試URP的抗干擾性能。實(shí)驗(yàn)平臺如圖10所示。

圖10 實(shí)驗(yàn)平臺Fig.10 Experimental platform

4.1 期望深度為0.4 m的定深控制實(shí)驗(yàn)

圖11和圖12所示分別為當(dāng)期望深度為0.4 m時URP在DSC-NDO控制器、DSC控制器和串級PID控制器下的運(yùn)動性能以及推進(jìn)器的響應(yīng)曲線。對圖11中4個通道的穩(wěn)態(tài)過程進(jìn)行定量分析。姿態(tài)角穩(wěn)定誤差范圍及各通道均方根誤差分別如表5和表6所示。

表5 期望深度為0.4 m時姿態(tài)通道穩(wěn)態(tài)誤差范圍對比Table 5 Comparison of steady-state error range of attitude channel with an expected depth of 0.4 m

表6 期望深度為0.4 m時各通道均方根誤差對比Table 6 Comparison of RMSE of each channel with an expected depth of 0.4 m

圖11 在DSC-NDO控制器、DSC控制器和串級PID控制器下期望深度為0.4 m的運(yùn)動性能Fig.11 Motion performances with desired depth of 0.4 m under DSC-NDO controller, DSC controller, and cascade PID

對比姿態(tài)通道的相關(guān)數(shù)據(jù)可知，在期望深度較小時，URP距離水底的距離較遠(yuǎn)，水底反沖力對于URP的影響較小。在DSC-NDO控制器下，3個姿態(tài)角的穩(wěn)態(tài)誤差范圍與DSC控制器下的相差不大，其控制精度略有提高；?、θ、ψ的均方根誤差相比于DSC控制器分別減小了7.9%、9.0%、7.2%，相比于串級PID控制器分別減小了17.1%、58.5%、51.6%。

在深度通道，由于測量噪聲的存在，最終控制輸出始終處于調(diào)節(jié)過程。在DSC-NDO控制器、DSC控制器和串級PID控制器下，z方向在穩(wěn)態(tài)后的誤差范圍分別為[-5，5] cm、[-5，6] cm、[-7，7] cm，相差不大。同時，深度通道的控制精度有所提高，采用本文方法所得均方根誤差相比于DSC控制器減小了8.2%，相比于串級PID控制器減小了25.4%。分析表明在較弱水底反沖擊力的干擾下，DSC-NDO控制器能在一定程度上補(bǔ)償干擾，穩(wěn)定性更好。當(dāng)平臺定深為0.4 m時，距離水面較近，推進(jìn)器會使水面產(chǎn)生一定的水波，但其波幅較小，對平臺所產(chǎn)生影響可忽略不計。

4.2 期望深度為0.9 m的定深控制實(shí)驗(yàn)

圖13和圖14所示分別為當(dāng)期望深度為0.9 m時URP在DSC-NDO控制器、DSC控制器和串級PID控制器下的運(yùn)動性能以及推進(jìn)器的響應(yīng)曲線。對圖13中4個通道的穩(wěn)態(tài)過程進(jìn)行定量分析。姿態(tài)角穩(wěn)定誤差范圍及各通道均方根誤差分別如表7和表8所示。

表8 期望深度為0.9 m時各通道均方根誤差對比Table 8 Comparison of RMSE of each channel with an expected depth of 0.9 m

圖13 在DSC-NDO控制器、DSC控制器和串級PID控制器下期望深度為0.9 m的運(yùn)動性能Fig.13 Motion performances with desired depth of 0.9 m under DSC-NDO controller, DSC controller, and cascade PID

圖14 在DSC-NDO控制器、DSC控制器和串級PID控制器下推進(jìn)器響應(yīng)曲線Fig.14 Thrusters response curves under DSC-NDO controller, DSC controller, and cascade PID

對比圖13中在不同控制器下定深過程中各個姿態(tài)角的變化可知，期望深度較大時，URP距離水底的距離較近，為0.3 m，水底反沖擊力對URP的影響較大，在其不確定干擾下，姿態(tài)系統(tǒng)均會存在一定穩(wěn)態(tài)誤差，但采用本文所提出方法時，3個姿態(tài)角的穩(wěn)態(tài)誤差范圍明顯比DSC和串級PID控制器的小，?、θ、ψ的均方根誤差相比于DSC控制器分別減小了24.2%、51.8%、38.8%，相比于串級PID控制器分別減小了28.1%、55.0%、61.1%。

在深度通道，由于測量噪聲的存在，最終控制輸出始終處于調(diào)節(jié)過程。3種控制器的響應(yīng)時間相差不大，但在本文所提出方法下z方向的震蕩幅度明顯比DSC控制器和串級PID控制器下的小。由于水底反沖擊擾動的影響，在DSC-NDO控制器、DSC控制器和串級PID控制器下，z方向的穩(wěn)態(tài)誤差范圍分別為[-5，5] cm、[-6，8] cm、[-10，10] cm，控制精度有較大提升。通過對深度通道穩(wěn)態(tài)過程的頻域特征進(jìn)行分析可知，經(jīng)過傅里葉變換，DSC-NDO控制器的振蕩頻率約為0.29 Hz，而DSC和串級PID控制器的振蕩頻率分別約為0.48 Hz和0.49 Hz，本文方法有效減小了定深運(yùn)動的震蕩幅度。同時，采用本文所提出的方法，深度通道的均方根誤差為2.36 cm，而其在DSC控制器和串級PID控制器下的均方根誤差分別為3.27 cm和3.56 cm，分別減小了27.8%和33.7%。分析表明，在較強(qiáng)水底反沖擊力的干擾下，DSC-NDO控制器能較好地降低干擾，提高平臺的穩(wěn)定性。

通過對比2組實(shí)驗(yàn)的測試結(jié)果可知，在深度為0.9 m(距水底0.3 m)的定深實(shí)驗(yàn)中，各通道的控制精度小于深度為0.4 m(距水底0.8 m)定深實(shí)驗(yàn)中的控制精度。定深位置越深，水底反沖擊力對于平臺的干擾越大，由于水底反沖擊力干擾持續(xù)存在于整個定深過程，使得靠近水底的定深實(shí)驗(yàn)誤差較大。但通過DSC-NDO控制器可提高URP在干擾環(huán)境下的定深穩(wěn)定性，具有較好的魯棒性。

因此，本文提出的基于干擾觀測器的動態(tài)面控制器(DSC-NDO)能夠在近水底反沖擊擾動的作用下有效提升定深過程中的控制效果，提高了在近水底干擾條件下的姿態(tài)通道和深度通道的穩(wěn)定性，證明了所提出的控制策略的優(yōu)越性與有效性，這與數(shù)值仿真的結(jié)果一致。

5 結(jié)論

1) 建立了水下旋翼式平臺的運(yùn)動學(xué)和動力學(xué)模型，模型中考慮了水動力影響，并根據(jù)動力學(xué)模型建立狀態(tài)方程用于控制器設(shè)計。

2) 針對具有內(nèi)外部非線性擾動的姿態(tài)通道和深度通道設(shè)計了基于干擾觀測器的動態(tài)面控制器，用于提高系統(tǒng)的魯棒性，同時，通過李雅普諾夫穩(wěn)定性理論證明了系統(tǒng)的穩(wěn)定性。

3) 在不同期望深度的定深控制實(shí)驗(yàn)中，本文所設(shè)計的控制器提高了姿態(tài)通道穩(wěn)定性和定深精度，降低了水底反沖擊力等內(nèi)外部干擾，驗(yàn)證了該算法具有更好的魯棒性和較強(qiáng)的抗干擾能力。