基于傾角反演的隧道斷面變形全方位監(jiān)測方法

陳曉斌，王風(fēng)棟，吳夢黎，王業(yè)順

(1.中南大學(xué) 土木工程學(xué)院，湖南 長沙，410082；2.重載鐵路工程結(jié)構(gòu)教育部重點(diǎn)實(shí)驗(yàn)室，湖南 長沙，410075)

隧道斷面變形是反映隧道健康狀況的關(guān)鍵因素[1-4]。傳統(tǒng)方法只在某一時(shí)刻記錄隧道斷面特定監(jiān)測點(diǎn)變形，很難準(zhǔn)確定位斷面危險(xiǎn)點(diǎn)位置并判別潛在的變形趨勢，難以滿足隧道健康狀況評估的需求[5-6]。為了實(shí)現(xiàn)整個(gè)隧道斷面的實(shí)時(shí)連續(xù)監(jiān)測，基于傾角傳感器和無線傳感網(wǎng)絡(luò)的隧道變形監(jiān)測方法成為當(dāng)前研究熱點(diǎn)[7-9]。20世紀(jì)90年代末便有學(xué)者利用傾角傳感器對隧道變形進(jìn)行監(jiān)測。BASSETT等[10]基于電解質(zhì)式傾角傳感器開發(fā)了巴塞特收斂系統(tǒng)(Bassett convergence system)，并在倫敦地鐵有限公司運(yùn)營隧道中進(jìn)行了試驗(yàn)驗(yàn)證。該系統(tǒng)主要由若干個(gè)帶有傾角傳感器的觀測臂組成，使用時(shí)，需將觀測臂首尾相連安裝到隧道斷面上。除此之外，ARIZNAVARRETA-FERNáNDEZ等[11]采用與巴塞特系統(tǒng)相似的原理開發(fā)了CANG(convergence by means of angular sensors)系統(tǒng)，并在雙車道公路隧道中進(jìn)行了試運(yùn)行。隨著MEMS(micro-electro-mechanical system)技術(shù)和無線傳感網(wǎng)絡(luò)技術(shù)的發(fā)展，基于MEMS傾角傳感器和無線傳感網(wǎng)絡(luò)的新型監(jiān)測方法開始用于隧道變形監(jiān)測。BENNETT等[12]使用傾角傳感器和裂縫計(jì)對倫敦地鐵隧道變形進(jìn)行了長期監(jiān)測。WANG等[13-14]采用無線傾角傳感器對上海地鐵隧道的水平和縱向收斂變形進(jìn)行了監(jiān)測。LI等[15]在隧道斷面頂部布設(shè)傾角傳感器，監(jiān)測了縱向沉降。同時(shí)，相關(guān)學(xué)者提出了多種基于傾角的變形計(jì)算方法。嵇中[16]假定隧道斷面變形為橢圓形，通過公式擬合的方法得到了盾構(gòu)隧道收斂變形的計(jì)算公式。HUANG等[17-18]通過定義“最優(yōu)測量點(diǎn)”，采用考慮管片變形的相對不轉(zhuǎn)動(dòng)點(diǎn)法對隧道收斂變形進(jìn)行計(jì)算。王明卓[19]通過建立數(shù)值模型，利用理論和數(shù)值擬合的方法建立了變形和傾角變化之間的關(guān)系。WANG等[5,14]則采用解析方法提出基于傾角傳感的盾構(gòu)隧道收斂計(jì)算方法，并利用誤差反演算法得到最優(yōu)安裝位置。

目前，提出的多種傾角-變形算法主要是用于計(jì)算特定監(jiān)測點(diǎn)變形，在準(zhǔn)確計(jì)算隧道斷面全方位變形(隧道斷面任意極角位置變形)方面還存在一些不足。巴塞特系統(tǒng)、CANG系統(tǒng)雖然可以實(shí)現(xiàn)全方位監(jiān)測，但需要大量的輔助設(shè)備，占用工作空間大，無法體現(xiàn)傾角傳感器體積小、易于安裝的優(yōu)勢。為了充分發(fā)揮傾角傳感器的優(yōu)勢，實(shí)現(xiàn)對隧道斷面全方位變形的實(shí)時(shí)連續(xù)監(jiān)測，本文提出一種新的基于傾角反演的隧道變形監(jiān)測方法，主要研究內(nèi)容包括：通過分析隧道變形與傾角之間的關(guān)系，推導(dǎo)隧道傾角-變形算法；開展傾角-變形算法誤差分析，增設(shè)假定約束條件，提出算法修正公式；建立三維有限差分?jǐn)?shù)值模型和室內(nèi)試驗(yàn)?zāi)Ｐ停ㄟ^數(shù)值模擬和室內(nèi)試驗(yàn)的方式驗(yàn)證算法的正確性，通過誤差分析討論其適應(yīng)性，為實(shí)際工程應(yīng)用提供依據(jù)和指導(dǎo)。

1 基于傾角的隧道變形算法

1.1 坐標(biāo)系選取

推導(dǎo)隧道傾角-變形算法時(shí)，首先需要選取合適的坐標(biāo)系來定義隧道各點(diǎn)的坐標(biāo)信息。常見隧道結(jié)構(gòu)一般由仰拱和上部拱形結(jié)構(gòu)組成，兩者的輪廓曲線均呈弧形。隧道仰拱的主要作用是將上部荷載傳遞給下部土體，同時(shí)抵抗下部土體的隆起，在實(shí)際監(jiān)測中，一般較少對仰拱進(jìn)行監(jiān)測。因此，本文在研究隧道變形過程中也僅針對上部拱形結(jié)構(gòu)。同時(shí)，考慮到隧道拱腳的變形較小，將上部拱形結(jié)構(gòu)兩底端近似看作固定約束[20]。

隧道上部拱形結(jié)構(gòu)的輪廓曲線上存在切線斜率無窮大的點(diǎn)，即存在傾角為90°的點(diǎn)。當(dāng)選用常用的直角坐標(biāo)系定義位置時(shí)，對斜率無窮大的點(diǎn)難以處理，同時(shí)也會存在同一x坐標(biāo)對應(yīng)多個(gè)y坐標(biāo)的問題即多值問題。為避免上述問題，采用極坐標(biāo)系來定義位置坐標(biāo)。如圖1所示，以2個(gè)拱腳連線的中點(diǎn)作為坐標(biāo)原點(diǎn)，記為極點(diǎn)O，從極點(diǎn)向右側(cè)拱腳引出1條射線作為極軸，記為極軸OX，以逆時(shí)針旋轉(zhuǎn)為正，建立極坐標(biāo)系。隧道輪廓曲線上各點(diǎn)的位置坐標(biāo)可以用極角φ和與其對應(yīng)的極徑r唯一表示，記為P(φ,r)。

圖1 坐標(biāo)系選取示意圖Fig.1 Diagram of coordinate system selection

1.2 傾角-變形算法推導(dǎo)

采用極坐標(biāo)表示隧道各點(diǎn)的位置，此時(shí)，隧道變形情況可以用各點(diǎn)的極徑變化量Δr表示，Δr越大，該點(diǎn)的變形量越大。利用傾角計(jì)算隧道變形時(shí)，需要建立傾角與變形之間的關(guān)系，通過已知傾角推算與之唯一對應(yīng)的變形值，用數(shù)學(xué)表達(dá)式表示為

式中：θ為隧道監(jiān)測點(diǎn)的傾角；Δr為隧道監(jiān)測點(diǎn)的變形量。下面推導(dǎo)Δr與θ的具體關(guān)系式。

為了便于分析，將隧道輪廓曲線的極角區(qū)間分為n個(gè)小區(qū)間，取其中1個(gè)小區(qū)間進(jìn)行分析。隧道分段變形幾何關(guān)系如圖2所示。設(shè)曲線AB為第i個(gè)小區(qū)間[φi-1,φi]所對應(yīng)的曲線分段，曲線A′B′為對應(yīng)變形后的曲線分段。

圖2 隧道分段變形幾何關(guān)系Fig.2 Deformation geometry relationship of tunnel segments

Pi(φi,ri)和Pi-1(φi-1,ri-1)是曲線分段的端點(diǎn)，對于變形前后的曲線分段，存在有函數(shù)關(guān)系Ri(φ)使得r=Ri(φ)，φ?[φi-1,φi]始終成立。但Ri(φ)的具體表達(dá)式并不明確，可以基于曲線插值的思想，構(gòu)造插值函數(shù)ri(φ)近似代替Ri(φ)，并使ri(φ)經(jīng)過端點(diǎn)Pi和Pi-1。任意曲線都可以構(gòu)造插值函數(shù)去近似代替實(shí)際曲線，各函數(shù)組成插值函數(shù)r(φ)?[0°,180°]。則隧道變形可以近似表示為

式中：Δr為隧道監(jiān)測點(diǎn)的變形量；r(φ)為變形后曲線的極徑；rc(φ)為曲線的初始極徑。

假設(shè)函數(shù)ri(φ)在區(qū)間[φi-1,φi]內(nèi)滿足二階連續(xù)，即函數(shù)圖像為光滑連續(xù)的曲線。以多項(xiàng)式為基函數(shù)構(gòu)造ri(φ)：

式中：aik為多項(xiàng)式的系數(shù)。式(3)的一階和二階導(dǎo)數(shù)r′i(φ)和r″i(φ)可以表示為：

如圖2所示第i個(gè)分段曲線，其極角區(qū)間為[φi-1,φi]，為方便計(jì)算，不妨將原函數(shù)進(jìn)行平移，設(shè)變量s=φ-φi-1，同時(shí)令si=φi-φi-1，則平移后的函數(shù)區(qū)間變?yōu)閇0,si]。分段端點(diǎn)Pi和Pi-1的極徑為ri和ri-1，ri(φ)在端點(diǎn)的一階導(dǎo)數(shù)值用r′i和r′i-1表示，可以得到以下關(guān)系：

將式(3)、(4)、(6)聯(lián)立可以得到：

同理，對于相鄰的第i+1段曲線，可以構(gòu)造函數(shù)ri+1(φ)，其中φ?[0,si+1]。2個(gè)函數(shù)在其區(qū)間內(nèi)均滿足二階連續(xù)，則在端點(diǎn)處有

將式(8)與式(5)聯(lián)立并將式(7)代入得

式(9)是關(guān)于r、r′的方程，由于采用傾角θ進(jìn)行隧道變形監(jiān)測，隧道各點(diǎn)的r和r′為未知量，要求解式(9)需要建立傾角θ與r、r′的關(guān)系。

極坐標(biāo)系與直角坐標(biāo)系的轉(zhuǎn)換關(guān)系為

此時(shí)，對于傾角θ，有

再由三角函數(shù)公式可得

將式(11)代入式(12)并化簡得

式(13)表征了傾角θ與r、r′的關(guān)系。將式(13)代入式(9)并化簡得

其中：

式(14)是關(guān)于r的方程組，求解前還需要2個(gè)邊界條件。設(shè)隧道2個(gè)拱腳滿足

式中：R0為隧道右側(cè)拱腳的極徑；Rn為隧道左側(cè)拱腳的極徑。R0與Rn為已知量，可以通過1次測量或者設(shè)計(jì)圖獲得。在將上部拱形結(jié)構(gòu)看作兩端固定約束的情況下，可以認(rèn)為R0與Rn為不變量。將式(15)與式(14)聯(lián)立為矩陣形式：

為表示方便，上式可以簡寫成

式中：A為系數(shù)矩陣，由隧道輪廓曲線各點(diǎn)的傾角θ求得；R為變量矩陣，是隧道各點(diǎn)極徑r組成的一維數(shù)組；B為結(jié)果矩陣。

式(17)是關(guān)于極徑r的方程組，根據(jù)矩陣的基本運(yùn)算法則可以求得變形后隧道各點(diǎn)的極徑：

同理，可以求得隧道初始極徑：

由此可以計(jì)算出隧道各點(diǎn)的變形量：

式中：ΔR為隧道各點(diǎn)變形量組成的一維數(shù)組。

式(20)即為傾角θ與隧道變形的關(guān)系，將實(shí)時(shí)獲得的隧道各監(jiān)測點(diǎn)的傾角代入式(20)便可以計(jì)算出隧道變形量。

將式(18)和式(19)求得的極徑代入式(7)可以得到系數(shù)ai1、ai2、ai3、ai4，將各系數(shù)代入式(3)可以得到隧道變形前后的隧道曲線rc(φ)和r(φ)，再利用式(2)即可求得隧道斷面曲線任意極角位置的變形量Δr，從而實(shí)現(xiàn)對隧道上部拱形結(jié)構(gòu)的全方位變形監(jiān)測。

1.3 監(jiān)測點(diǎn)極角修正

在實(shí)際應(yīng)用中，為考慮成本，一般使用便攜式小型傾角傳感器對隧道若干個(gè)監(jiān)測點(diǎn)傾角進(jìn)行監(jiān)測，這可能造成計(jì)算誤差。計(jì)算誤差一方面來源于傾角傳感器本身結(jié)構(gòu)，其輸出的傾角是傳感器所在直線的傾角，與實(shí)際監(jiān)測點(diǎn)的傾角之間存在一定誤差。但傾角傳感器的長度一般為10～20 cm，相對于隧道周長，傳感器長度小，因而這類誤差影響較小。另一方面，在隧道變形過程中，傳感器伴隨隧道一起發(fā)生位置變動(dòng)，但由于隧道各點(diǎn)的位移方向并非均指向極點(diǎn)，會促使變形前后的監(jiān)測點(diǎn)極角發(fā)生變化，如圖3所示。

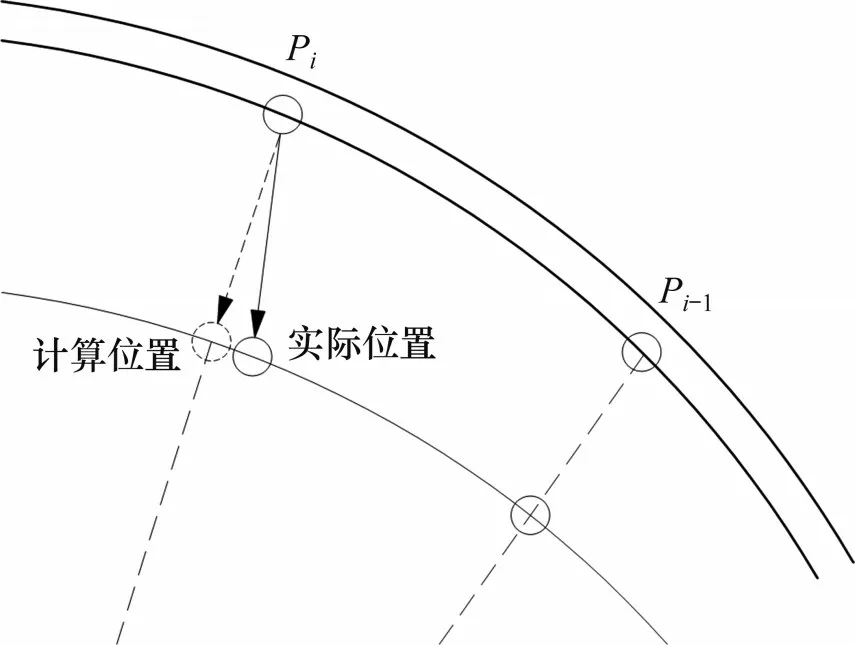
圖3 監(jiān)測點(diǎn)位置變動(dòng)示意圖Fig.3 Diagram of location change of the monitoring point

而在計(jì)算過程中，若仍然使用初始極角進(jìn)行計(jì)算，則很有可能產(chǎn)生較大的計(jì)算誤差，同時(shí)，由于每個(gè)監(jiān)測點(diǎn)的極角均會發(fā)生變化，還會造成累計(jì)誤差。

為了減小傾角-變形算法在有限監(jiān)測點(diǎn)下的計(jì)算誤差，可以通過補(bǔ)充假設(shè)和約束條件的方式對隧道變形后的極角進(jìn)行修正，并將修正后的極角重新代入傾角-變形算法，從而改進(jìn)算法的計(jì)算結(jié)果。

根據(jù)隧道變形前后的形狀特點(diǎn)，補(bǔ)充假設(shè)條件：隧道變形前后相鄰2個(gè)傳感器間的弧長相對于總弧長的比例不變。令變形前隧道上部拱形結(jié)構(gòu)總弧長和相鄰2個(gè)傳感器間的分段弧長分別為s、li，變形后為s′、li′，則補(bǔ)充的假設(shè)條件可以用數(shù)學(xué)表達(dá)式表示為

根據(jù)極坐標(biāo)下的弧長積分公式可以得到

式中：Φi為修正后的傾角。通過補(bǔ)充假設(shè)條件，利用式(21)和式(22)即可實(shí)現(xiàn)對傾角-變形算法計(jì)算結(jié)果的修正。

2 有限差分算例

2.1 有限差分模型建立

以某隧道斷面設(shè)計(jì)為參考，建立Flac 3D數(shù)值模型，如圖4所示(其中，R為半徑)。斷面形狀為三心圓，半徑分別為R1=5.7 m，R2=R3=8.2 m，|下側(cè)角度α=12°，厚度為0.35 m，底部固定約束。采用彈性本構(gòu)模型，C25混凝土力學(xué)參數(shù)選取如表1所示。

表1 C25混凝土物理力學(xué)參數(shù)Table 1 Mechanical parameters of numerical model of C25 concrete

圖4 隧道數(shù)值模型Fig.4 Tunnel numerical model

傾角傳感器通過梁結(jié)構(gòu)單元模擬。梁結(jié)構(gòu)單元兩端采用固定鏈接，當(dāng)模型發(fā)生變形時(shí)，結(jié)構(gòu)單元位置隨之產(chǎn)生相應(yīng)變動(dòng)。輸出結(jié)構(gòu)單元端點(diǎn)的x、y坐標(biāo)，則隧道變形前后結(jié)構(gòu)單元的傾角可以按下式計(jì)算：

式中：θ和θ′分別為變形前后結(jié)構(gòu)單元的傾角；(x1，y1)和(x2，y2)分別為變形前結(jié)構(gòu)單元端點(diǎn)坐標(biāo)；(x1′，y1′)和(x2′，y2′)分別為變形后結(jié)構(gòu)單元端點(diǎn)坐標(biāo)；Δθ為傾角變化量。

2.2 計(jì)算結(jié)果分析

在隧道模型內(nèi)側(cè)對稱設(shè)置10個(gè)結(jié)構(gòu)單元，以傳感器所在位置為邊界劃分出9個(gè)極角區(qū)間，在隧道模型上施加1×104kN·m-2的法向均布荷載，隧道發(fā)生變形，待變形穩(wěn)定后輸出隧道的位移云圖，如圖5(a)所示。輸出結(jié)構(gòu)單元的端點(diǎn)坐標(biāo)并計(jì)算傾角，在不進(jìn)行極角修正的情況下，使用推導(dǎo)的傾角-變形算法計(jì)算得到隧道各點(diǎn)的極徑變化量Δr，并將其與數(shù)值模擬值進(jìn)行對比，如圖5(b)所示。

圖5 均布荷載下隧道變形計(jì)算結(jié)果Fig.5 Deformation results of tunnel under uniform load

從圖5(b)可以看出：算法計(jì)算得到的隧道變形量在極角90°位置最大，向兩端逐漸減小，這與數(shù)值模擬結(jié)果基本相同。但未經(jīng)極角修正情況下的計(jì)算結(jié)果與模擬值相比存在明顯誤差，不符合監(jiān)測需求。

使用1.3節(jié)所述極角修正方法對算例的計(jì)算結(jié)果進(jìn)行修正，得到結(jié)果如圖6所示。從圖6可以看出：修正后的計(jì)算誤差相比于修正前明顯減小，且僅需2次迭代修正，計(jì)算結(jié)果便與數(shù)值模擬結(jié)果基本吻合。

圖6 經(jīng)過迭代修正后的極徑變化量計(jì)算結(jié)果Fig.6 Deformation results after iterative correction

為了進(jìn)一步量化評價(jià)算法的計(jì)算誤差，采用最大絕對誤差和平均相對誤差這2個(gè)評價(jià)指標(biāo)對計(jì)算結(jié)果進(jìn)行評價(jià)。用Δr(φ)表示算法計(jì)算得到的隧道變形量，ΔR(φ)表示數(shù)值模擬得到的理論變形量，則最大絕對誤差和平均相對誤差可以表示為：

式中：Emax為最大絕對誤差；δ為平均相對誤差。

但實(shí)際計(jì)算中Δr(φ)與ΔR(φ)往往較復(fù)雜，難以進(jìn)行積分運(yùn)算。為了計(jì)算方便，可以選取曲線上的若干點(diǎn)，采用離散的方法來近似求得平均相對誤差，即

將計(jì)算結(jié)果與數(shù)值模擬結(jié)果代入式(26)，得到不同迭代修正次數(shù)下隧道變形計(jì)算的平均相對誤差，如圖7所示。從圖7可以看出：隨著迭代修正次數(shù)增加，誤差逐漸減小并最終趨于穩(wěn)定，穩(wěn)定后隧道變形計(jì)算平均相對誤差為3.64%(低于5%)，同時(shí)，計(jì)算出穩(wěn)定后隧道變形計(jì)算的最大絕對誤差為0.178 mm，證明了傾角-變形算法的準(zhǔn)確性。在實(shí)際使用中，為了保證計(jì)算結(jié)果準(zhǔn)確性，應(yīng)按照修正方法進(jìn)行至少3次迭代修正。此外，在修正過程中只對傳感器極角進(jìn)行修正，沒有改變傳感器的傾角輸出值，也驗(yàn)證了1.3節(jié)中極角修正假設(shè)的正確性。

圖7 不同修正次數(shù)下的隧道變形計(jì)算平均相對誤差Fig.7 Average relative errors of tunnel depormation caculation in different correction times

3 傾角-變形算法適應(yīng)性分析

算例模型的荷載形式為對稱均布荷載，但在實(shí)際隧道工程中，隧道斷面所受荷載形式可能更加復(fù)雜，因此，需要驗(yàn)證傾角-變形算法在不同工況下的適應(yīng)性。隧道所受荷載類型可以大致分為均布荷載、對稱非均布荷載和非對稱荷載[21]3種形式。這里采用第2節(jié)有限差分隧道模型模擬對稱非均布荷載和非對稱荷載這2種工況。

3.1 對稱非均布荷載工況模擬

對于對稱非均布荷載工況，在原有1×104kN·m-2均布荷載的基礎(chǔ)上增加0.1×104kN·m-2中間荷載，以此模擬非均布荷載類型。隧道模型參數(shù)和傳感器位置與均布荷載工況保持一致，最終得到該工況下的隧道位移云圖如圖8(a)所示，可以看出，由于施加了額外荷載，隧道的變形與均布荷載下有明顯不同，整體呈豎向壓扁形式。

圖8 對稱非均布荷載下隧道變形計(jì)算結(jié)果Fig.8 Deformation results of tunnel under symmetrical non-uniform load

輸出傳感器的傾角，代入傾角-變形算法，同樣進(jìn)行3次迭代修正，得到隧道各點(diǎn)的變形量Δr，并繪制出極徑變化量Δr與極角的關(guān)系曲線，如圖8(b)所示。從圖8(b)可以看出：對稱非均布荷載工況下算法極徑變化量計(jì)算值與數(shù)值模擬值基本一致，代入式(22)與式(24)計(jì)算得到當(dāng)前工況下隧道變形的最大絕對誤差為0.424 mm，平均相對誤差為6.07%，計(jì)算誤差較小。

3.2 非對稱荷載工況模擬

在1×104kN·m-2均布荷載的基礎(chǔ)上，通過在模型右側(cè)增加0.05×104kN·m-2荷載的方式模擬非對稱荷載，變形穩(wěn)定后輸出隧道位移云圖如圖9(a)所示。將傳感器傾角代入傾角-變形算法，繪制非對稱荷載工況下Δr與極角的關(guān)系曲線，如圖9(b)所示。從圖9可見：在該工況下，算法計(jì)算的隧道變形最大絕對誤差為0.706 mm，平均相對誤差為4.95%，說明傾角-變形算法在非對稱荷載工況下同樣具有較好的適應(yīng)性。

圖9 非對稱荷載下隧道變形計(jì)算結(jié)果Fig.9 Deformation results of tunnel under asymmetric load

通過分析上述3種工況可知：算法在不同工況下的測量精度有所不同，其中，均布荷載工況的計(jì)算誤差最小，最大絕對誤差僅為0.178 mm，平均相對誤差僅為3.66%；非均布荷載算法的計(jì)算誤差較大；從整體平均誤差看，對稱非均布荷載工況下的平均相對誤差最大，為6.07%；從局部監(jiān)測點(diǎn)的最大誤差角度看，非對稱荷載工況下的誤差最大，為0.706 mm。雖然算法在不同工況下的誤差不盡相同，但都保持在較低值，最大絕對誤差均不超過1 mm，平均相對誤差小于7%。

4 試驗(yàn)驗(yàn)證

通過有限差分算例分析算法自身誤差后，這里采用室內(nèi)試驗(yàn)方式驗(yàn)證算法在實(shí)際使用過程中隧道變形監(jiān)測的準(zhǔn)確性。

4.1 試驗(yàn)設(shè)計(jì)

室內(nèi)試驗(yàn)設(shè)計(jì)如圖10(a)所示。模型尺寸參考第2.1節(jié)中數(shù)值模型尺寸進(jìn)行縮尺設(shè)計(jì)，縮尺比為1:5。縮尺后隧道高為1.48 m，最大寬度為2.28 m。由于所用傾角-變形算法與隧道自身的材料性質(zhì)無關(guān)，同時(shí)，為簡化試驗(yàn)過程，試驗(yàn)?zāi)Ｐ筒捎?0 mm普通螺紋鋼筋及5 mm鋼板拼接而成，如圖10(b)所示。在模型內(nèi)側(cè)預(yù)留有10個(gè)監(jiān)測點(diǎn)位，用于安裝傾角傳感器(C1、C2、…、C10為傳感器編號)。

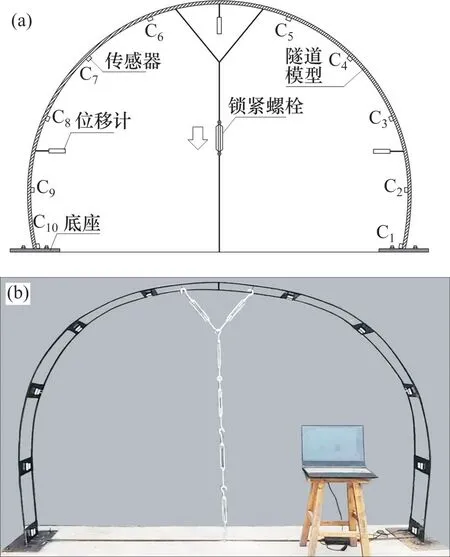
圖10 室內(nèi)模型試驗(yàn)Fig.10 Indoor model test

試驗(yàn)以鎖緊螺栓作為加載裝置，通過對模型施加豎直或水平方向上的拉力使其發(fā)生變形，模擬隧道拱頂沉降和水平收斂。加載通過變形控制，共設(shè)置10個(gè)加載等級，控制模型變形從0 mm逐級增大到50 mm，試驗(yàn)時(shí)，緩慢加載以保證傳感器測量準(zhǔn)確。受試驗(yàn)條件限制，模型試驗(yàn)無法像數(shù)值模擬一樣輸出隧道所有極角位置的實(shí)際變形，因此，僅對2個(gè)具有代表性的隧道變形指標(biāo)進(jìn)行實(shí)際監(jiān)測。選取隧道拱頂沉降和水平收斂[22-23]作為監(jiān)測指標(biāo)，將3個(gè)位移計(jì)分別設(shè)置于模型的拱頂和拱腰位置，3個(gè)位移測點(diǎn)記為W1、W2和W3，記錄試驗(yàn)過程中模型豎直和水平方向上的位移，其中，拱頂沉降通過位移計(jì)直接讀取，水平收斂則通過讀取水平方向上的2個(gè)位移相加獲得。

傳感器的布置如圖10(a)所示。以右側(cè)拱腳為起始點(diǎn)在模型內(nèi)側(cè)設(shè)置10個(gè)傳感器，依次編號為C1～C10。起始監(jiān)測點(diǎn)對應(yīng)的極角為0°，末尾對應(yīng)極角180°，兩側(cè)監(jiān)測點(diǎn)基本呈對稱布置，記錄試驗(yàn)過程中各監(jiān)測點(diǎn)產(chǎn)生的傾角。

4.2 試驗(yàn)結(jié)果與分析

圖11所示為試驗(yàn)加載過程中各傾角傳感器的傾角變化量。由于模型結(jié)構(gòu)和加載基本對稱，故所得傾角變化也基本對稱，其中傳感器C4、C5、C6和C7處的傾角變化呈減小趨勢，傳感器C1、C2、C9和C10處的傾角變化呈增大趨勢，傳感器C3與C8處的傾角變化不明顯，且拱頂附近傾角變化比拱腳處的傾角變化大。根據(jù)加載方式，可以初步判斷傾角傳感器的測量趨勢正確。

圖11 不同加載等級下傳感器傾角變化量Fig.11 Variation of inclination under different loading levels

將傳感器所測結(jié)果代入傾角-變形算法計(jì)算位移測點(diǎn)W1、W2和W3在極坐標(biāo)下的變形量，分別記為Δr1、Δr2和Δr3。為了能與位移計(jì)所測位移相比較，利用極坐標(biāo)與直角坐標(biāo)的轉(zhuǎn)換關(guān)系對所得Δr1、Δr2和Δr3進(jìn)行直角坐標(biāo)轉(zhuǎn)換，轉(zhuǎn)換關(guān)系為

式中：Δxi和Δyi分別為測點(diǎn)i在直角坐標(biāo)系x和y方向上的位移，mm；Δri為測點(diǎn)i在極坐標(biāo)下的變形量，mm；φi為測點(diǎn)i所在極角。

利用式(27)計(jì)算得到3個(gè)位移測點(diǎn)在直角坐標(biāo)系下的位移，其中，Δy2為隧道模型的拱頂沉降，Δx1與Δx2的和為隧道的水平收斂。將得到的拱頂沉降和水平收斂與位移計(jì)所測的實(shí)際值進(jìn)行比較，如圖12所示。

圖12 隧道模型變形監(jiān)測結(jié)果Fig.12 Monitoring results of tunnel deformation

從圖12可以看出：利用本文方法得到的拱頂沉降和水平收斂與實(shí)際結(jié)果接近，可以正確反映試驗(yàn)過程中測點(diǎn)的位移變化趨勢。拱頂沉降的平均測量誤差為7.34%(小于8%)，水平收斂的平均測量誤差為4.10%(小于5%)。由于傳感器測量誤差的存在，試驗(yàn)誤差比數(shù)值模擬誤差大，但仍較小。

5 結(jié)論

1) 通過設(shè)立合適的坐標(biāo)系和假設(shè)條件，隧道變形與傾角之間可以建立數(shù)學(xué)關(guān)系，并據(jù)此可得到隧道傾角-變形計(jì)算方法。

2) 監(jiān)測點(diǎn)的極角隨隧道變形而改變，直接影響傾角-變形算法計(jì)算精度。假定隧道變形前后相鄰2個(gè)傳感器間弧長與總弧長的比例不變，修正極角，則只需2次迭代修正，即可將計(jì)算誤差降低到5%以下。

3) 隧道傾角-變形算法在均布荷載、對稱非均布荷載和非對稱荷載等工況中均具有良好的適應(yīng)性和較高的準(zhǔn)確性，其最大絕對誤差小于1 mm，平均相對誤差小于7%。

4) 即使存在傳感器測量誤差，隧道傾角-變形算法仍具有較高的監(jiān)測精度，豎向拱頂沉降監(jiān)測誤差小于8%，水平收斂監(jiān)測誤差小于5%。