格柵節點加強對風積沙筋土界面力學性能的影響

杜煒，聶如松,2，譚永長，張杰，祁延錄，趙春彥

(1.中南大學 土木工程學院，湖南 長沙，410075；2.中南大學 重載鐵路工程結構教育部重點實驗室，湖南 長沙，410075；3.新疆鐵道勘察設計院有限公司，新疆 烏魯木齊，830011)

土工格柵加筋土結構因其具有良好的力學性能，廣泛運用于工程實踐中[1-2]。筋土界面的相互作用行為對加筋土結構穩定性有直接影響，格柵縱肋、橫肋提供的摩擦阻力和被動抗阻力可有效地約束土體移動。TANG等[3-4]認為拉拔試驗是研究土工格柵加筋土結構荷載傳遞機制和計算相關參數的較好方法。國內外研究者通過拉拔試驗，對筋土相互作用特性進行了研究。LOPES等[5]研究了圍壓、填料密度、拉拔速度對單向土工格柵抗拔性能的影響，從拉拔試驗結果發現隨著圍壓、填料密度或拉拔速度增大，拉拔阻力增大。AHMADI等[6]制作了4種不同孔徑的土工格柵，與5種不同級配曲線的道砟相互組合進行拉拔試驗，發現不同級配的道砟均存在1個最優孔徑，若孔徑過小，則會減弱土工格柵與道砟的嵌鎖作用，導致拉拔阻力降低；若孔徑過大，則會減弱土工格柵與填料間的摩擦力，導致拉拔阻力下降。曹文昭等[7]開展拉拔試驗，對比研究了雙向土工格柵和三向土工格柵的加筋性能，發現雙向土工格柵應變更加均勻，三向土工格柵的應變集中在拉拔端附近。苗晨曦等[8]對不同網孔類型土工格柵的剪切帶、接觸力鏈、細觀組構、筋材軸力分布等細觀特性進行了討論，認為不同界面法向壓力下應采用不同的網孔形狀。王志杰等[9]研究了加載方式對筋土界面細觀特性的影響，發現采用剛性頂部加載方式所得結果與柔性頂部加載方式所得結果存在明顯區別。

隨著研究不斷深入，土工合成材料結構形式趨于三維化。張孟喜等[10]提出了立體加筋的概念，制定了多種立體加筋的方案，通過三軸壓縮試驗研究了加筋形式和加筋高度對砂土強度的影響。李磊等[11]將不同厚度的土工膜固定在土工格柵節點上，形成了具有立體加筋效果的加強節點土工格柵，通過開展一系列拉拔試驗，研究了加強節點厚度與極限拉拔阻力增量的關系，認為在一定范圍內兩者呈線性關系，且橫肋間距和法向應力對相關系數有影響。邱成春等[12]基于離散元法建立了二維的路堤數值模型，研究了加強節點土工格柵加筋路堤的細觀特征，與無筋路堤和普通格柵加筋路堤相比，加強節點土工格柵加筋路堤的累積沉降更小，內部應力分布更均勻。張孟喜等[13]研究了節點布置方式對拉拔試驗結果的影響，發現當厚度一定時，上下兩側各布置一半厚度節點的方式優于上側布置節點的方式，但不能解釋節點布置方式影響試驗結果的作用機理。BEYRANVAND等[14]在土工格柵上黏附混凝土塊，展開土工格柵加筋砂土的拉拔試驗，通過黏附混凝土塊提升了格柵的被動抗阻力。這些研究以普通土工格柵為研究對象，大多局限于宏觀層面，對加強節點改善土工格柵加筋性能的細觀機理尚不明確。為此，本文作者采用離散元軟件PFC建立加強節點加筋風積沙拉拔試驗的數值模型，研究節點布置方式影響試驗結果的作用機理，證實節點群體效應的存在，得出最優的相鄰節點間距；工程中常采用經驗的方法鋪設土工格柵，會造成一定程度的浪費，為此，對普通土工格柵與加強節點土工格柵的剪切帶范圍進行對比分析，評價不同加強節點厚度土工格柵的立體加筋效果，以便為加強節點土工格柵的鋪設間距提供參考。

1 試驗流程與參數標定

1.1 試驗流程與模擬思路

開展風積沙的靜三軸壓縮試驗，建立三軸試驗數值模型，根據三軸試驗結果進行參數反演，確定風積沙的細觀參數。開展土工格柵的單肋條拉伸試驗，建立單肋條拉伸試驗的數值模型，確定土工格柵的細觀參數。建立普通土工格柵加筋風積沙拉拔試驗的數值模型，代入風積沙和土工格柵的參數，依據拉拔試驗結果驗證數值模型的合理性，在拉拔試驗數值模型的基礎上展開進一步研究。

1.2 風積沙細觀參數標定

室內試驗填料為風積沙，取自塔克拉瑪干沙漠。風積沙數碼照片和電鏡掃描照片見圖1，風積沙基本物理特性參數見表1。三軸試驗在TSZ全自動三軸儀上進行，試樣直徑為39.1 mm，高度為80.0 mm。制樣過程依據GB/T 50123—2019《土工試驗方法標準》執行。研究表明[15]，因風積沙強度低、黏聚力小，制樣時建議不要在飽和器底部墊濾紙及四周涂抹凡士林，制樣完成后立即開展試驗，以避免取樣時大量沙土黏在飽和器四周，造成試樣不完整。試樣在最優含水率狀態下按壓實系數K=0.93制備，在30 kPa圍壓下開展固結不排水靜三軸壓縮試驗。

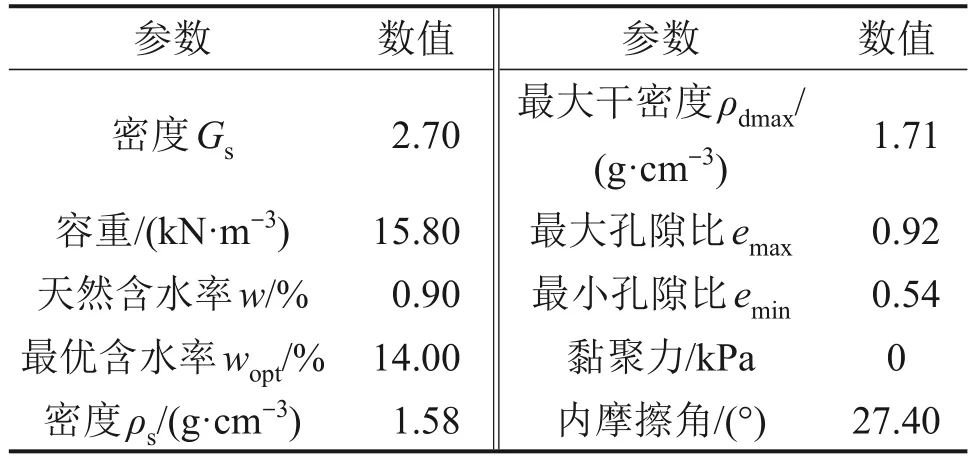
表1 風積沙物理特性參數Table 1 Physical parameters of aeolian sand

圖1 塔克拉瑪干沙漠風積沙照片Fig.1 Photos of aeolian sand in Taklamakan Desert

圖2所示為三軸試驗物理模型和數值模型。初始狀態下數值模型中試樣高度為80 mm，直徑為39.1 mm。三軸數值模型尺寸與物理模型尺寸保持一致。柔性膜顆粒之間接觸采用線性黏結接觸模型，組成柔性膜的顆粒半徑取0.64 mm，表2所示為柔性膜的細觀參數，主要參考了橡膠膜的拉伸試驗的參數[16]，由于不考慮柔性膜破壞的情況，柔性膜采用較高的黏結強度。采用光滑球體模擬風積沙顆粒，雖然風積沙顆粒相對均勻，但仍有肉眼不可見的棱角。為了使模擬結果盡可能地與實際結果匹配，風積沙采用抗轉動接觸模型，考慮實際顆粒不規則形狀。通過多次試算，反復改變顆粒變形模量、摩擦因數及相關顆粒參數，直到模擬結果與試驗結果相近。最終選取具有42 159個顆粒的試樣，該數量足以反映材料特性。風積沙之間的接觸以及風積沙與土工格柵的接觸均采用表3中參數。圖3所示為三軸試驗標定結果(圍壓為30 kPa)，從圖3可見：體應變-軸向應變在加載初期較接近，隨著軸向應變增大，模擬結果與試驗結果差別變大，偏應力-軸向應變曲線整體的發展趨勢基本相同，誤差較小。

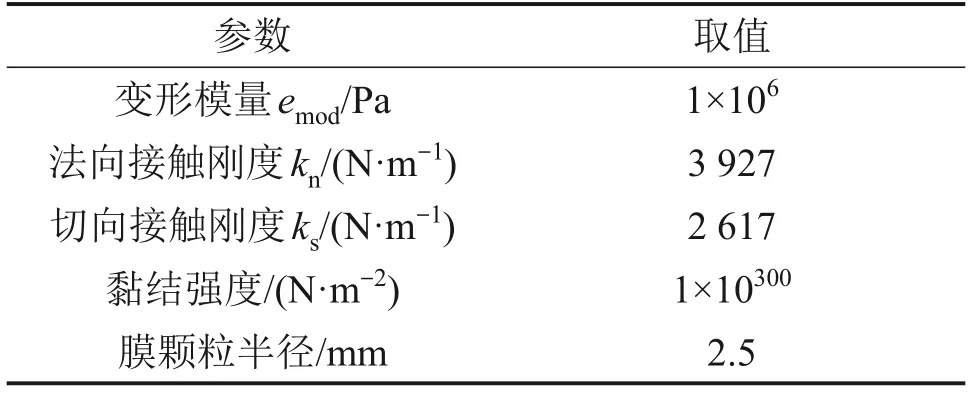
表2 膜顆粒接觸模型細觀參數Table 2 Mesoscopic parameters of flexible films

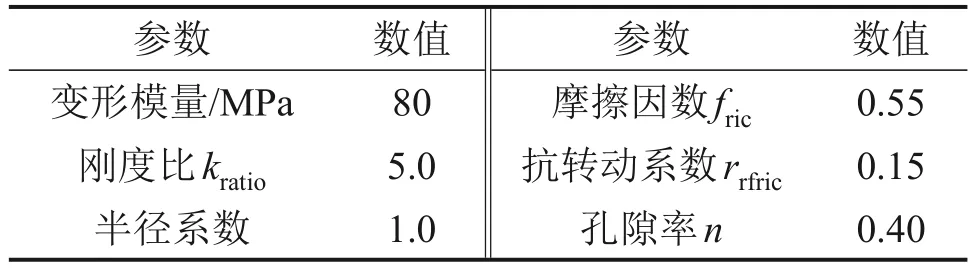
表3 風積沙標定參數Table 3 Calibration parameters of aeolian sand

圖2 三軸物理模型及其顆粒流模擬Fig.2 Physical model of triaxial test and particle flow simulation

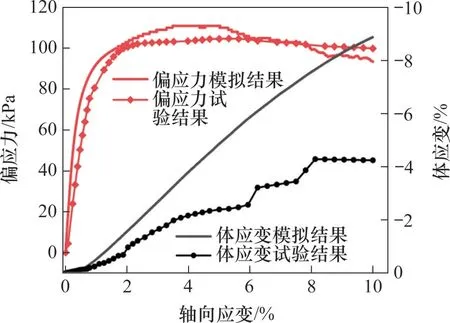
圖3 偏應力-軸向應變和體應變-軸向應變曲線Fig.3 Deviatoric stress-axial strain and volume strainaxial strain relationship curves

1.3 土工格柵參數標定

本試驗所用格柵為雙向土工格柵，如圖4(a)所示。采用單肋法測試，試樣在儀器上的標距為235 mm，拉伸速度為50 mm/min，在橫肋、縱肋各取5個試樣。試驗嚴格按照國家標準規定的步驟進行。格柵尺寸和單肋條拉伸試驗測得的宏觀力學參數見表4。如圖4(b)所示，編號1～7代表埋置在有效區域的7條橫肋。格柵顆粒間采用平行黏結接觸模型，平行黏結接觸模型受拉不受壓，能較好地模擬土工格柵拉伸強度高的特點。模擬土工格柵采用的細觀參數見表5。普通土工格柵實測與計算的拉伸強度-應變關系曲線見圖5，從圖5可見應力計算結果與實測結果較吻合。

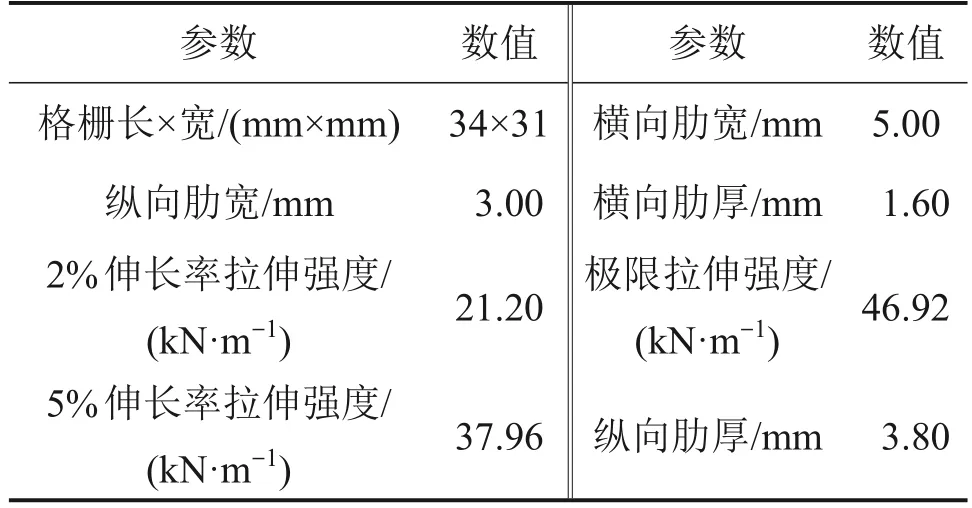
表4 土工格柵尺寸及力學參數Table 4 Geogrid dimensions and mechanical parameters

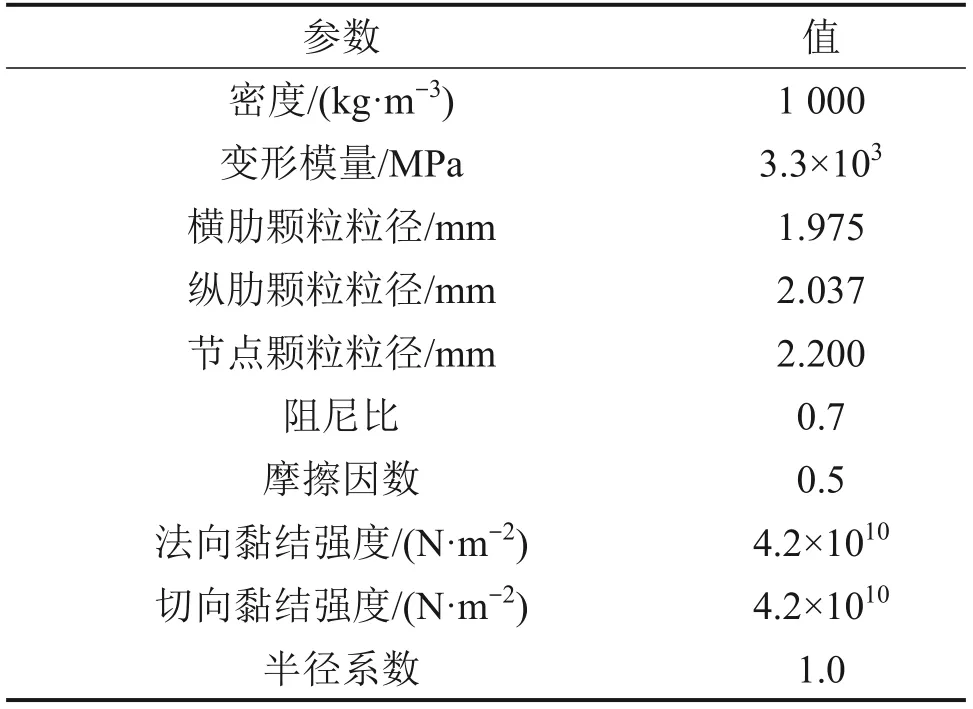
表5 土工格柵細觀參數Table 5 Meso-parameters of geogrid

圖4 土工格柵圖Fig.4 Drawing of geogrid

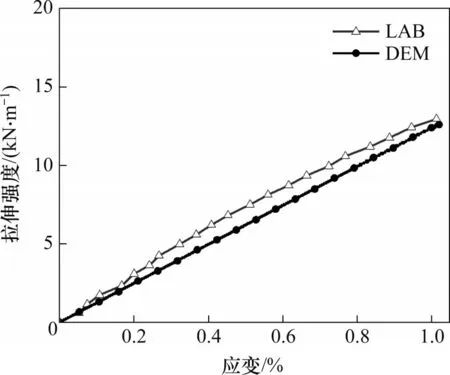
圖5 土工格柵的拉伸強度-應變關系對比Fig.5 Comparison of tensile strength-strain relationship of geogrid

2 拉拔試驗及其數值模型

2.1 室內拉拔試驗

圖6所示為YT1200S型直剪拉拔摩擦儀，試驗箱長×寬×高為250 mm×200 mm×200 mm。試驗填土共分4次填入壓平，每層填土高度為50 mm。土工格柵為不具有加強節點的普通格柵，土工格柵長度取280 mm，在土體中的長度為250 mm，剩余30 mm預留長度的格柵用于與夾具連接。土工格柵的寬度為150 mm，與試驗箱兩側各保持25 mm距離。填入2層土樣并找平，安裝土工格柵。安裝時，在拉拔出口涂抹潤滑劑以免造成卡口影響試樣結果。然后，繼續分層填筑至試驗箱頂面，此時，填土高度為200 mm。將剛性荷載板置于已填筑好的試樣土體頂面，施加法向壓力，持續維持法向壓力15 min，使風積沙-土工格柵緊密接觸，再進行拉拔試驗。考慮到土工格柵埋置在路基不同深度位置，據文獻[17]，拉拔試驗法向壓力確定為15、30和60 kPa，拉拔速度為0.5 mm/min，當拉拔端位移達15 mm時終止試驗。對同一類土樣、同一法向壓力下的試樣進行5組平行試驗，通過綜合比較以降低試驗結果的離散性。

圖6 直剪拉拔摩擦儀Fig.6 Pull-out test apparatus

2.2 拉拔試驗數值模型

拉拔試驗數值模型與物理試驗幾何尺寸一致。受計算機算力的限制，模擬顆粒往往要放大數十倍，以提高計算效率。但這種方法明顯降低了計算精度，且已有研究證明[18]：當放大倍數過高時，模擬顆粒體積較大，其沿筋材轉動和滑動，在拉拔過程中不斷形成密實的顆粒排列狀態，導致出現峰后拉拔力大幅度波動的情況。為研究放大倍數的影響，參考文獻[19]，構建分層風積沙數值模型，越接近土工格柵，放大倍數越小，將算力集中于筋土核心區域并構建均質風積沙數值模型。采用顆粒排斥法生成土樣，顆粒級配假定呈線性分布。圖7(a)所示為生成分層風積沙數值模型，將風積沙分為5層，顆粒數量為64 425個。圖7(b)所示為均質風積沙數值模型，顆粒粒徑分布范圍為4.5～7.5 mm，中值粒徑d50為5.98 mm，顆粒數量為50 041個。模擬顆粒與現實風積沙的級配曲線如圖8所示。從圖8可見：在分層風積沙數值模型中，筋土界面附近的風積沙顆粒放大倍數最小，顆粒粒徑分布范圍為1.6～5.2 mm，中值粒徑d50為3.4 mm，厚度為35 mm；第2層和第4層的顆粒粒徑分布范圍為5.7～7.5 mm，厚度為35 mm；第1層和第5層的顆粒粒徑分布范圍為6.75～11.25 mm，厚度約為80 mm。理論研究表明，只要選取尺度相關的微觀本構，放大粒徑試樣與原粒徑試樣便具有相同的力學響應，但應保證三維模擬單元試驗顆粒數目大于40 000個[20]，且顆粒集合體外觀直徑與內部顆粒平均粒徑的比值在計算能力允許的情況下應盡可能地大，但不應小于30[21]。利用Fish函數賦予拉拔端固定水平速度，MIAO等[22-23]取拉拔速度為0.375 m/s。經多次試算，當拉拔速度小于1 m/s時，拉拔位移-拉拔力曲線趨于穩定。本文取拉拔速度為0.2 m/s，將土工格柵拔出15 mm時終止計算。記錄拉拔力、拉拔位移、孔隙率、格柵應變的變化，在拉拔過程中，每100 s步記錄1次參量。

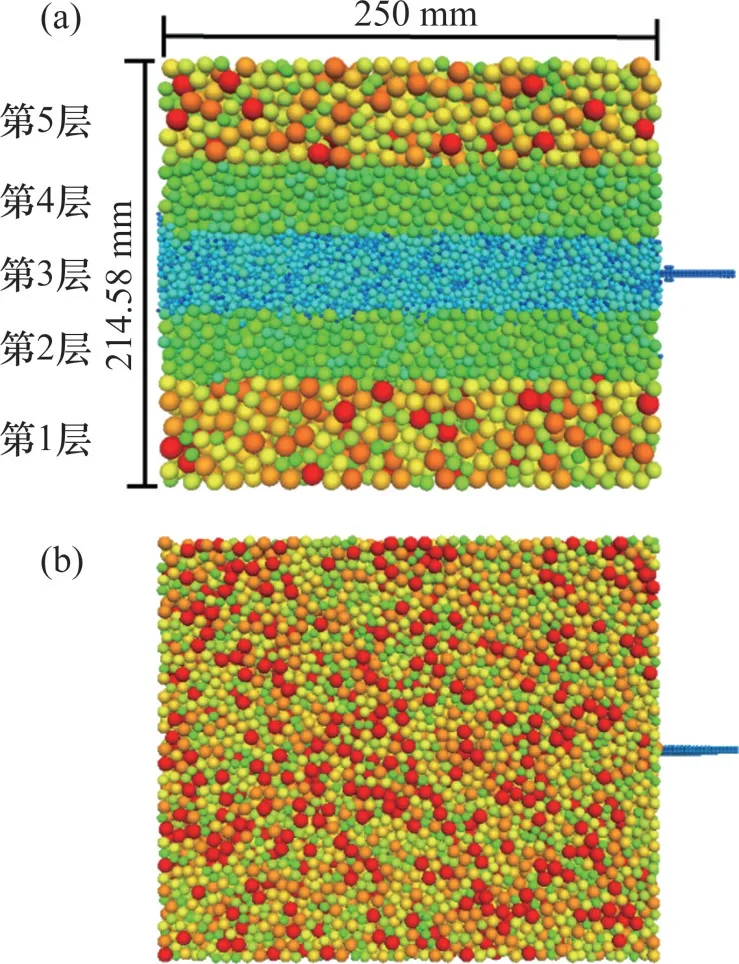
圖7 風積沙數值模型Fig.7 Numerical models of aeolian sand

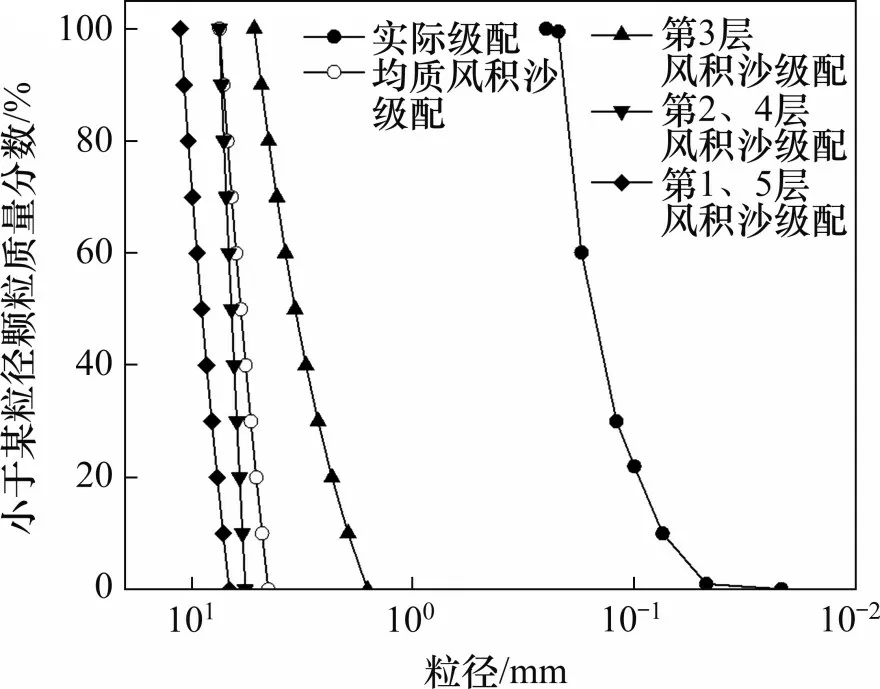
圖8 模擬顆粒與現實風積沙的級配曲線Fig.8 Gradation curves of simulated particle and aeolian sand

2.3 數值模型的驗證

圖9所示為分層風積沙數值模型、均質風積沙數值模型和室內試驗的拉拔阻力與位移的關系曲線。從圖9可見：總體上看，試驗初期曲線近似呈線性增大；隨著拉拔端位移增大，拉拔力的增速逐漸降低；到達峰值后，數值模擬結果呈現出小幅度的波動下降趨勢；隨著法向壓力增大，曲線整體升高，與峰值所對應的拉拔位移也越大；在同一法向壓力下，模擬曲線與試驗曲線較接近，發展規律相似，擬合度較高，證明分層風積沙數值模型和均質風積沙數值模型的合理性；當法向壓力為15 kPa和30 kPa時，均質風積沙數值模型的拉拔力-拉拔位移曲線整體略高于分層風積沙數值模型曲線；當法向壓力為60 kPa時，均質風積沙數值模型的拉拔力明顯偏高，均質風積沙模型的拉拔端附近存在粒徑較大的顆粒，導致格柵在拉拔過程中容易卡口，剛性前壁附近的應力集中現象更顯著。整體上看，與均質風積沙數值模型相比，分層風積沙數值模型結果更接近于室內試驗結果，證明了分層風積沙數值模型的優越性。

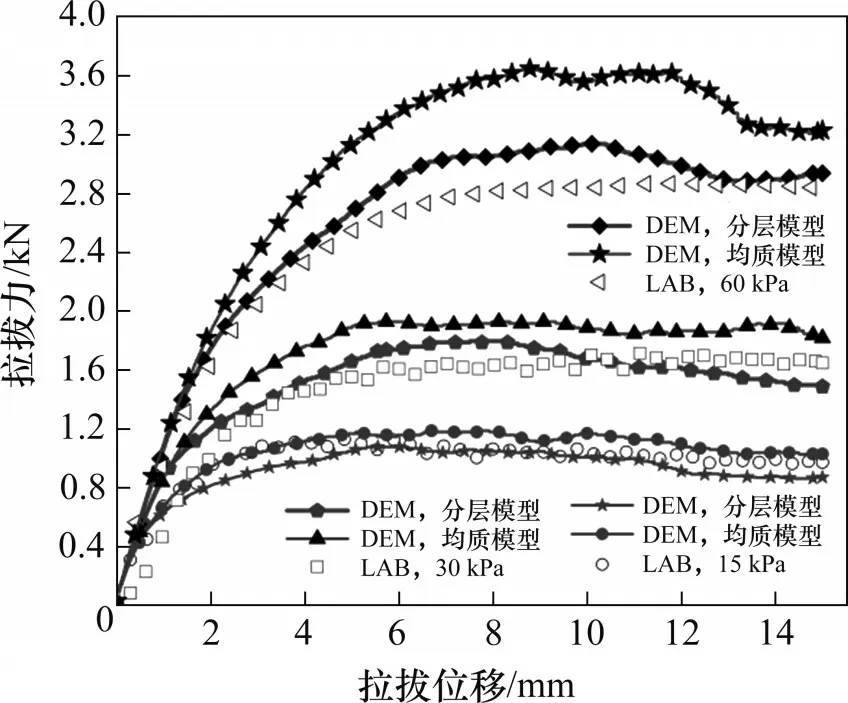
圖9 拉拔力與拉拔位移的關系Fig.9 Relation between pull-out force and pull-out displacement

2.4 加強節點及計算工況

為研究節點排布方式對筋土界面的力學影響，共考慮3種型式：格柵節點上、下兩側分別加強和兩側同時加強。不同節點布置方式如圖10所示。格柵節點加強工況見表6。

表6 試驗工況Table 6 Test cases

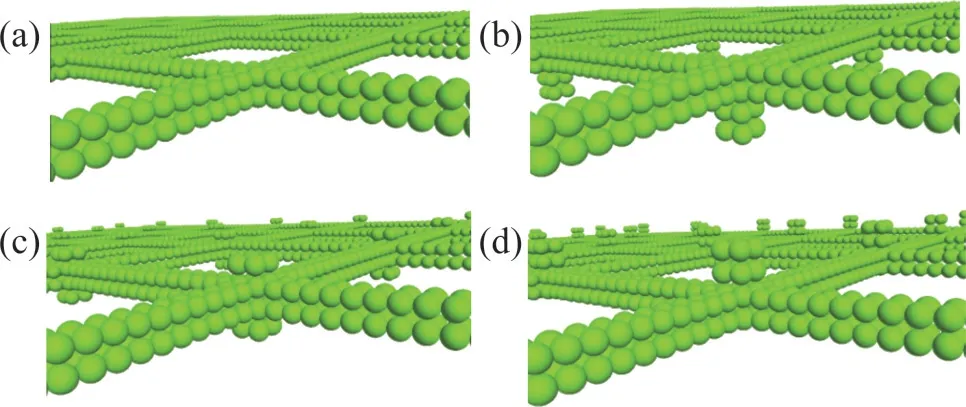
圖10 不同節點布置方式Fig.10 Different node arrangements

3 計算結果分析

3.1 節點加強方式對極限抗拔阻力的影響

不同法向壓力和節點布置方式下的拉拔阻力與位移的關系見圖11。從圖11可知，加強節點顯著提高了土工格柵的極限拉拔阻力；以30 kPa法向壓力的工況為例，普通土工格柵的極限拉拔阻力為1 800 N，工況B的極限拉拔阻力為1 910 N，相比于普通格柵提高了6.11%。工況D的極限拉拔阻力為1 930 N，相比于普通格柵提高了7.22%；工況C的極限拉拔阻力為1 960 N，相比于普通格柵提高了8.89%；當材料用量一定時，與工況B和D相比，工況C中土工格柵的極限拉拔阻力增幅最大，不同的法向壓力下均呈現出類似的規律。

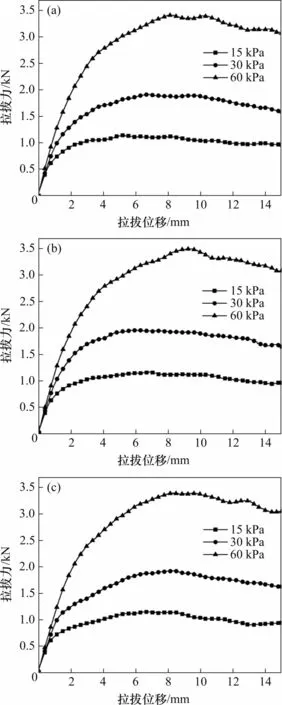
圖11 不同節點布置方式下拉拔阻力與位移的關系Fig.11 Relationship between pull-out force and pull-out displacement in different node layouts

JEWELL等[24]提出了經典的刺入剪切破壞模式，ALAGIYAWANNA等[25]發現拉拔阻力的刺入剪切理論值與試驗值在低法向壓力下較接近，法向壓力較高時差異較大。設σb為橫肋的承載應力，其計算式如下：

式中：σ'n為土工格柵受到的法向壓力，包括加載板施加的恒定法向壓力與上覆風積沙重力產生的法向壓力；φ為風積沙的內摩擦角(rad)。計算得到σb的具體值后，加強節點提供的極限拉拔阻力增量T可依據下式[13]計算：

式中：H為加強節點的厚度；W為加強節點的寬度；N為節點的數量。基于刺入剪切破壞理論，極限拉拔阻力增量理論解與數值解的對比見圖12。從圖12可見：當法向壓力為15 kPa和30 kPa時，理論解與數值解的差異較小；當法向壓力為60 kPa時，工況B的極限拉拔阻力增量數值解較接近理論解，工況C的結果偏大，工況D的結果偏小。總體上看，不同工況下的極限拉拔阻力增量數值解與理論解較接近，證明圖10中模擬節點方法是合理的。

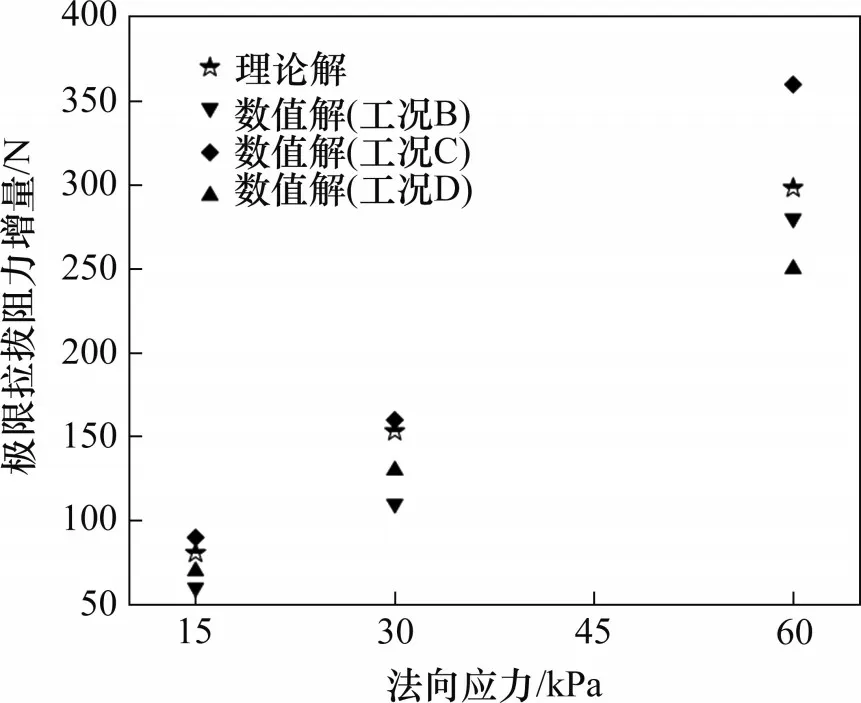
圖12 極限拉拔阻力增量數值解與理論解對比Fig.12 Comparison of numerical and theoretical solutions for increment of ultimate pull-out resistance

3.2 節點加強方式對筋土界面強度參數的影響

剪切強度-法向壓力擬合曲線見圖13。基于靜力平衡和筋土界面剪應力均勻分布假設，依據

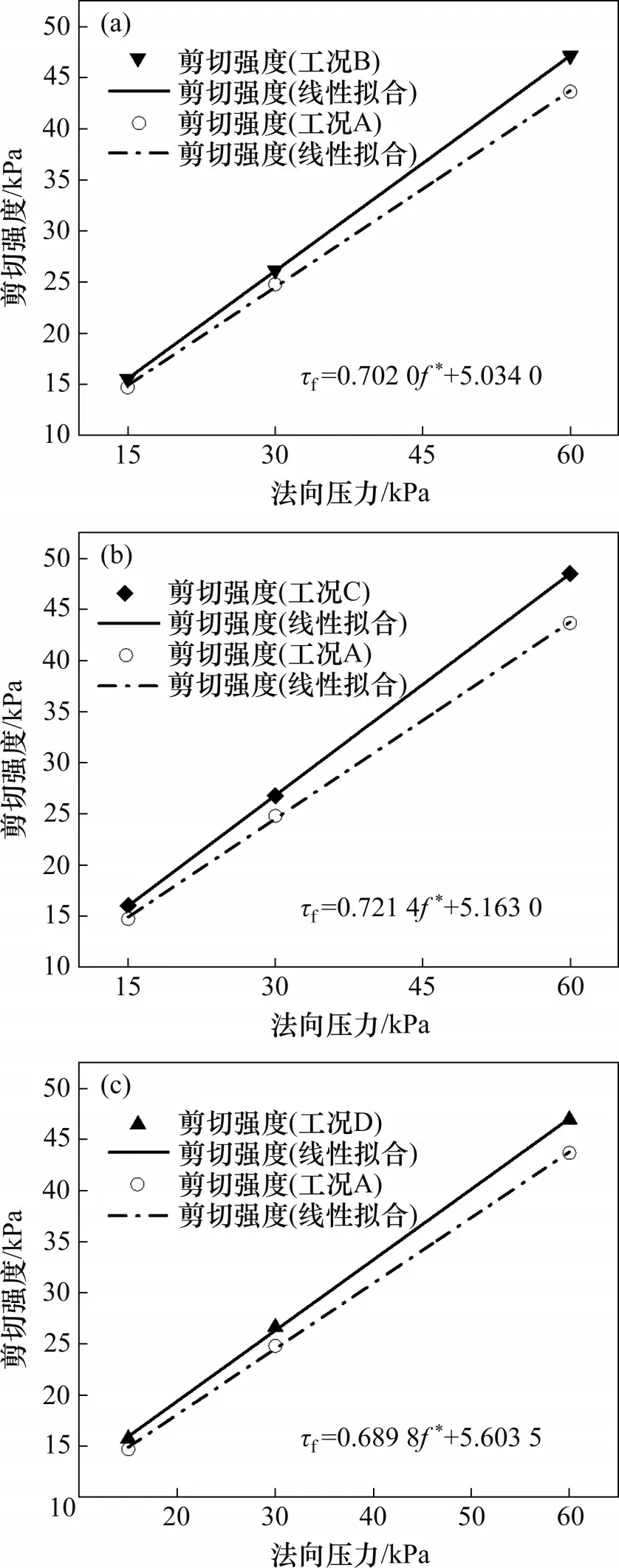
圖13 剪切強度-法向壓力擬合曲線Fig.13 Shear strength-normal pressure fitting curves

對界面剪切強度與法向壓力關系進行線性擬合，反算界面強度指標。式(3)中，τf為界面剪切摩擦強度；σn為法向應力，f*為似摩擦因數，Csg為似黏聚力。不同節點布置方式下的界面摩擦強度參數如表7所示。從表7可以看出：普通格柵和加強節點格柵的似黏聚力變化很小，在5.1～5.6 kPa之間波動，因而，節點加強對似黏聚力的影響很小，可以忽略不計。節點加強后，界面摩擦角增大2°～3°；當節點上下兩側同時加厚時，界面摩擦角的增幅最大。

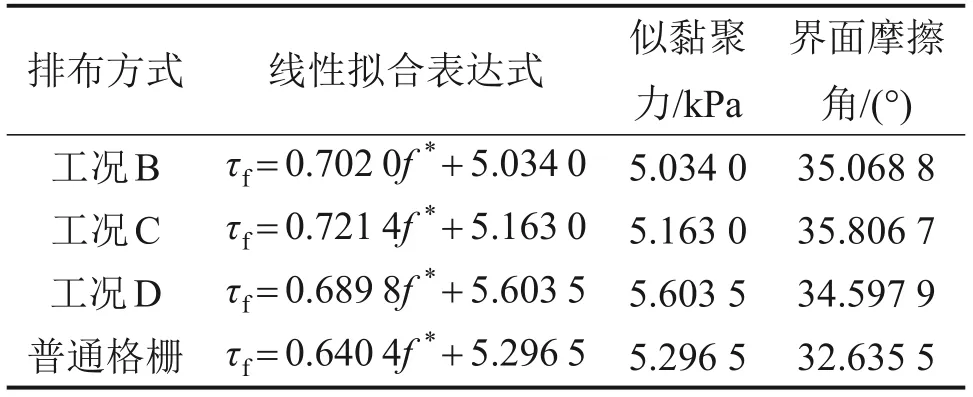
表7 不同節點布置方式下的界面摩擦強度參數Table 7 Interface strength parameters under under different node arrangements

3.3 加強節點厚度對極限抗拔阻力的影響

不同加強節點厚度下的拉拔力-拉拔位移曲線關系見圖14(法向壓力為30 kPa)。工況C中土工格柵的極限拉拔阻力為1 960 N，相比于普通格柵(工況A)峰值提高8.89%，單位厚度加強節點對峰值的提高率為2.02%。工況E中土工格柵的極限拉拔阻力為2 130 N，峰值提高18.33%，單位厚度節點對峰值的提高率為2.08%。工況F中土工格柵的極限拉拔阻力為2 260 N，峰值提高了25.56%，單位厚度節點對峰值的提高率為1.94%。工況G中土工格柵的極限拉拔阻力為2 430 N，峰值提高了35.00%，單位厚度節點對峰值的提高率為1.99%；當節點厚度變大時，節點提供的極限拉拔阻力增量增大，單位厚度節點對峰值的提高率變化不大。節點增厚厚度與極限拉拔阻力增量的關系曲線見圖15，其中，T為極限拉拔阻力增量，H為節點增厚厚度，節點增厚厚度指上側加厚厚度與下側加厚厚度之和。從圖15可以看出：節點增厚厚度H與極限拉拔阻力增量具有良好的線性關系。

圖14 不同加強節點厚度下的拉拔力-拉拔位移曲線Fig.14 Pull-out force versus pull-out displacement curves of different thicknesses of strengthened nodes

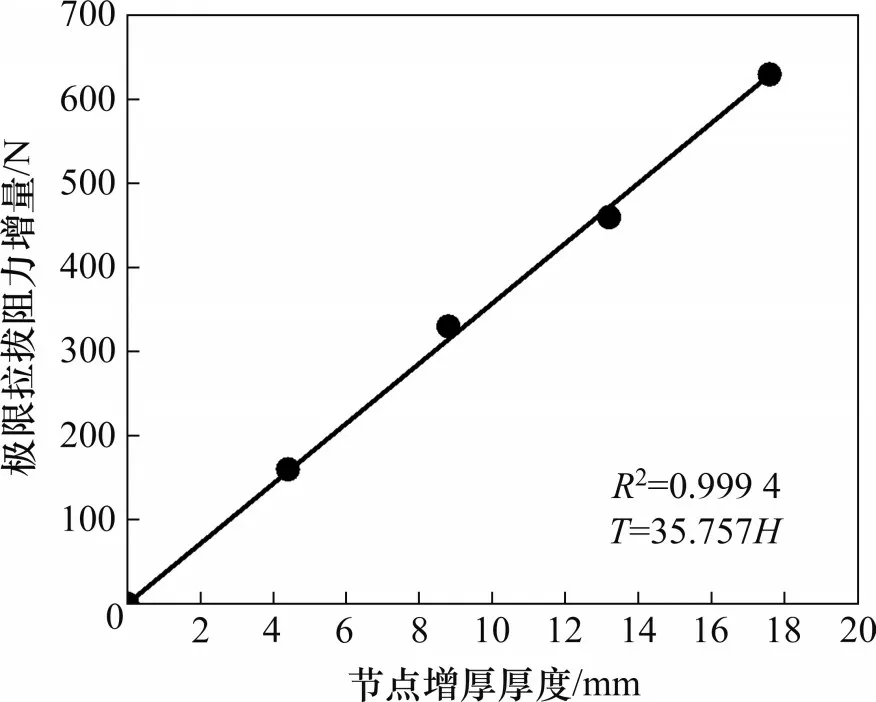
圖15 節點增厚厚度與極限拉拔阻力增量的關系Fig.15 Relationship between node thickness and ultimate pull-out resistance increment

3.4 加強節點厚度對格柵應變的影響

沿拉拔方向，土工格柵的應變情況差異很大，有必要將土工格柵分為前、中、后3段(見圖4(b))，每段長度約為93.3 mm。不同節點厚度土工格柵的應變變化規律(法向壓力為30 kPa)見圖16。從圖16可見：總體上看，不同工況下格柵前段的應變最大，格柵中段的應變其次，格柵后段的應變最小；格柵前段應變的曲線形狀最接近拉拔力-拉拔位移曲線的形狀，說明格柵前段承擔了較多的拉拔阻力。不同加強節點厚度土工格柵的分段峰值應變如表8所示。從表8可見：與普通格柵(工況A)相比，工況C格柵前、中、后段的峰值應變分別增大了10.45%、9.15%、14.67%；工況E格柵前、中、后段的峰值應變分別增大了21.64%、22.00%、18.67%；工況F格柵前、中、后段的峰值應變分別增大了33.13%、23.53%、40.89%；工況G格柵前、中、后段的峰值應變分別增大了46.72%、37.25%、45.78%。加強節點顯著提高了格柵每段的應變率，更充分地利用了格柵的加筋性能，且加強節點的厚度越大，格柵每段的應變峰值越大。分段峰值應變增量與節點增厚厚度關系曲線見圖17，可見格柵分段峰值應變與節點增厚厚度有良好的線性關系。由線性擬合表達式斜率可知，格柵前段的峰值應變增長速度為格柵中段的1.81倍，是格柵后段增長速度的2.83倍。說明節點厚度增量對格柵前段的影響更強烈，越靠近拉拔端，節點厚度增量的影響越顯著。

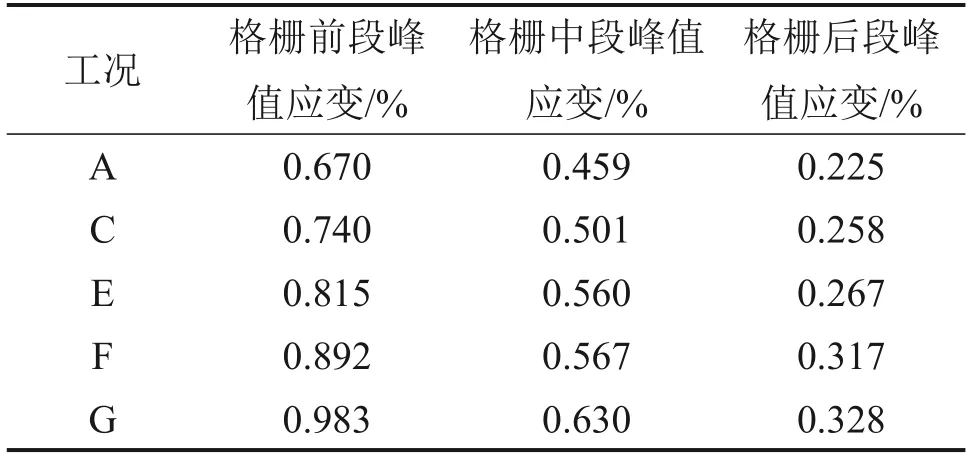
表8 不同工況土工格柵的分段峰值應變Table 8 Sectional peak strain of geogrid under different conditions

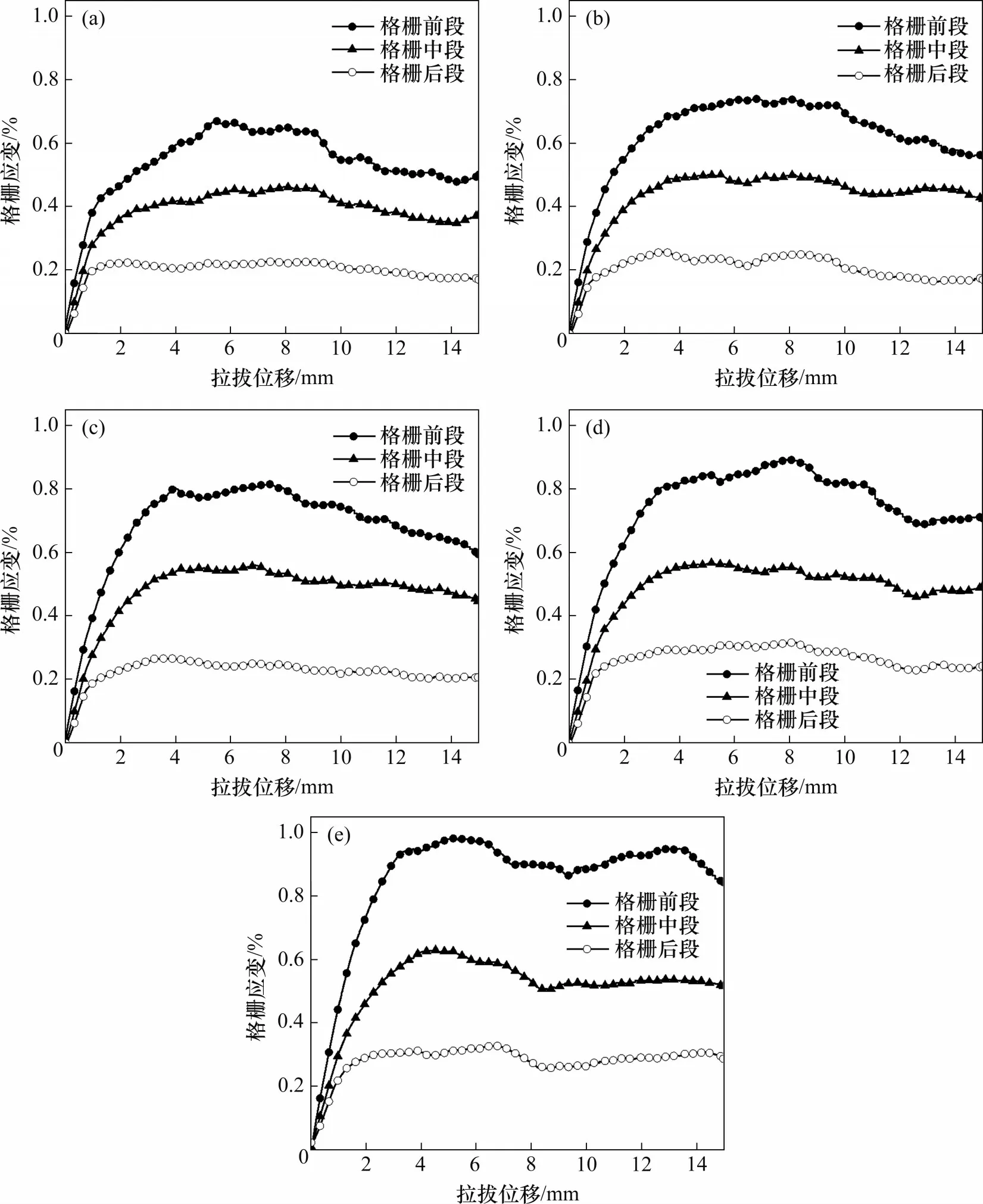
圖16 不同節點厚度土工格柵的應變變化規律Fig.16 Strain variation laws of geogrids with different node thicknesses

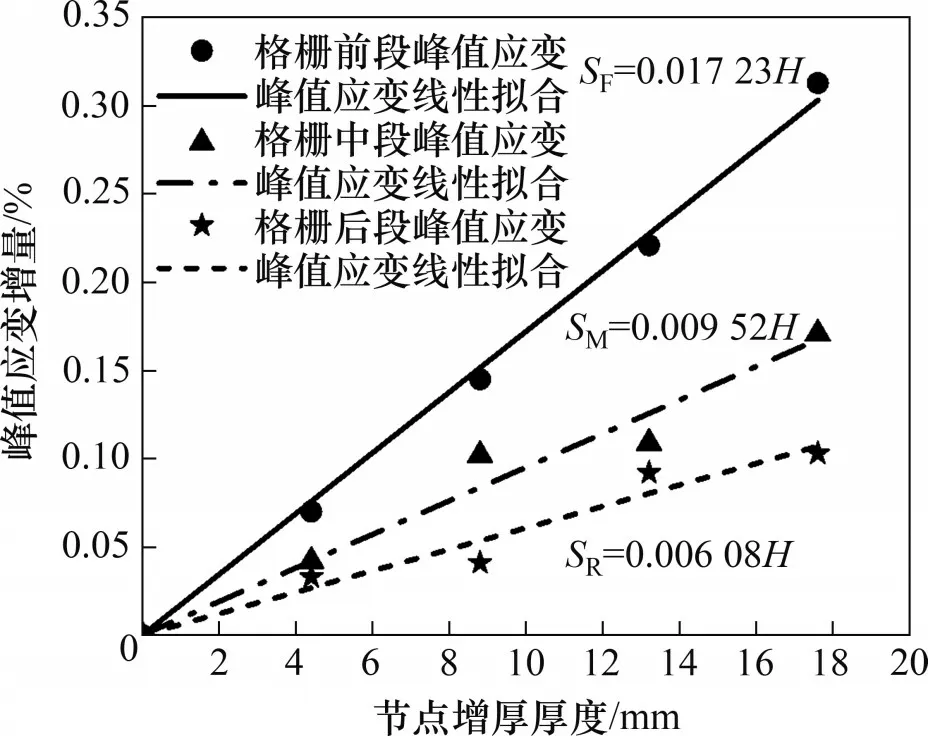
圖17 峰值應變增量與節點厚度增量關系曲線Fig.17 Curves of relationship between peak strain increment and node thickness increment

3.5 加強節點厚度對筋土界面孔隙率的影響

在筋土界面布置55個直徑為2.5 cm的測量球，通過測量球可測得筋土界面孔隙率的變化規律，如圖18所示。拉拔前后筋土界面處局部孔隙率和試樣體積的變化情況見表9。從圖18和表9可見：拉拔結束后，對于普通土工格柵的工況，筋土界面的孔隙率上升7.82%，風積沙試樣體積上升了0.28%；工況C中筋土界面的孔隙率上升了9.09%，試樣體積上升了0.48%，體積變化率為普通格柵的1.74倍；工況E中筋土界面的孔隙率上升了10.04%，試樣體積上升了0.58%，體積變化率為普通格柵的2.08倍；工況F中筋土界面的孔隙率上升了9.33%，試樣體積上升了0.57%，體積變化率為普通格柵的2.06倍；工況G中筋土界面的孔隙率上升了9.30%，試樣體積上升了0.70%，體積變化率為普通格柵的2.50倍。與普通土工格柵相比，加強節點土工格柵對界面處風積沙的擾動更強烈，試樣整體的剪脹趨勢更加顯著。

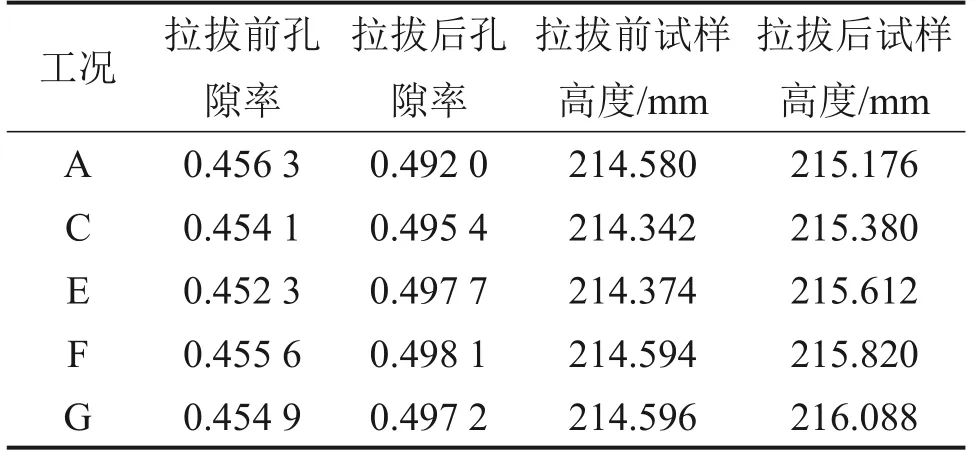
表9 筋土界面處局部孔隙率和試樣體積變化Table 9 Local porosity and sample volume change at interface between reinforcement and soil

圖18 測量球布置位置Fig.18 Measuring ball arrangement position

3.6 加強節點厚度對接觸力鏈的影響

將接觸力鏈按比例顯示，投影到XOZ平面上，得出2種工況拉拔結束后的力鏈分布情況，如圖19所示。從圖19可見：工況A和工況G表現的整體分布規律相似，剛性后壁附近存在明顯的應力空洞，剛性前壁附近則存在應力集中現象，且越靠近前壁，應力集中現象越明顯。力鏈在橫肋附近表現為鋸齒狀分布。與工況A相比，工況G在拉拔端附近的應力集中現象更加顯著，說明工況G的土工格柵對風積沙的影響程度更大。

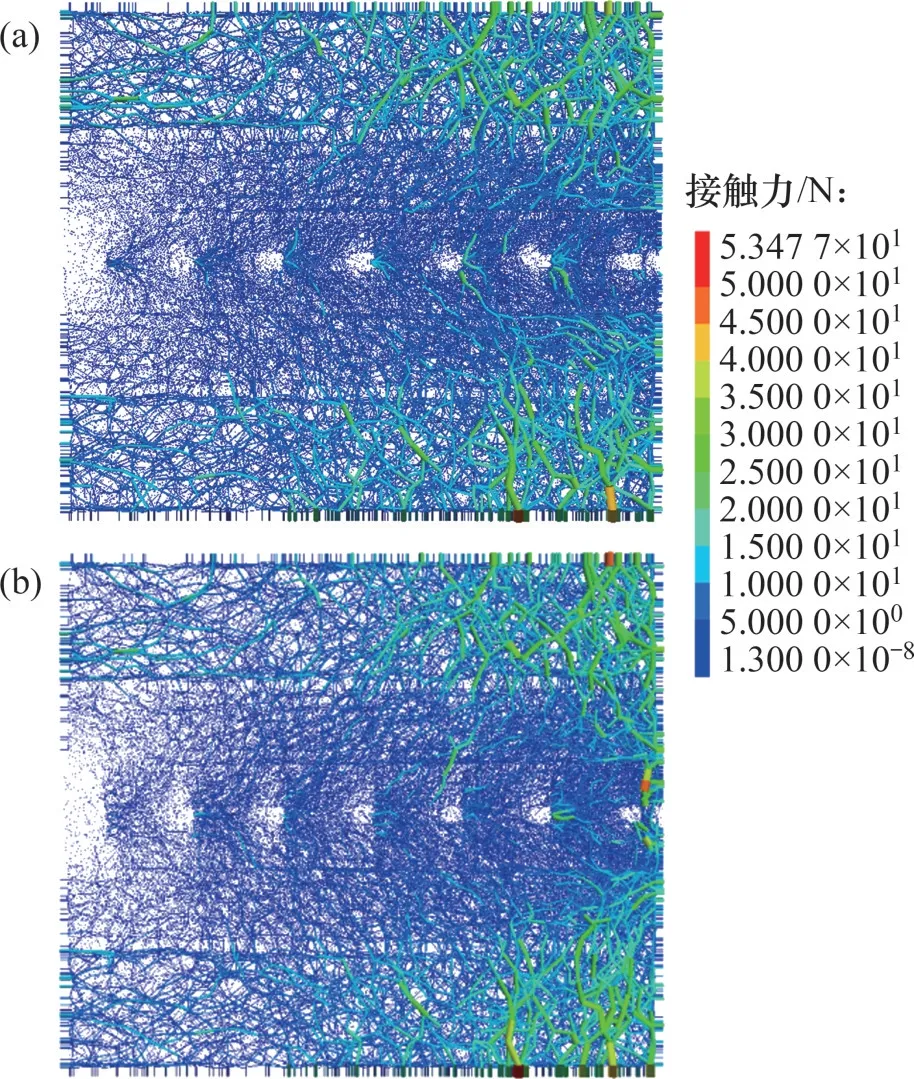
圖19 2種工況下的力鏈分布Fig.19 Force chain distribution in two conditions

3.7 加強節點厚度對剪切帶范圍的影響

普通格柵和工況G的格柵拔出15 mm時(法向壓力為30 kPa)的風積沙顆粒位移矢量圖見圖20。從圖20可見：總體上看，格柵前段附近的剪切帶厚度比雙格柵后段附近的剪切帶厚度略大；在剪切帶范圍外，風積沙顆粒在格柵前段的運動更加劇烈，格柵后段附近顆粒受到的影響較小。對比圖20(a)和(b)可知：工況G的剪切帶范圍比普通格柵的剪切帶范圍略大，且在剪切帶范圍外的顆粒運動更加劇烈。

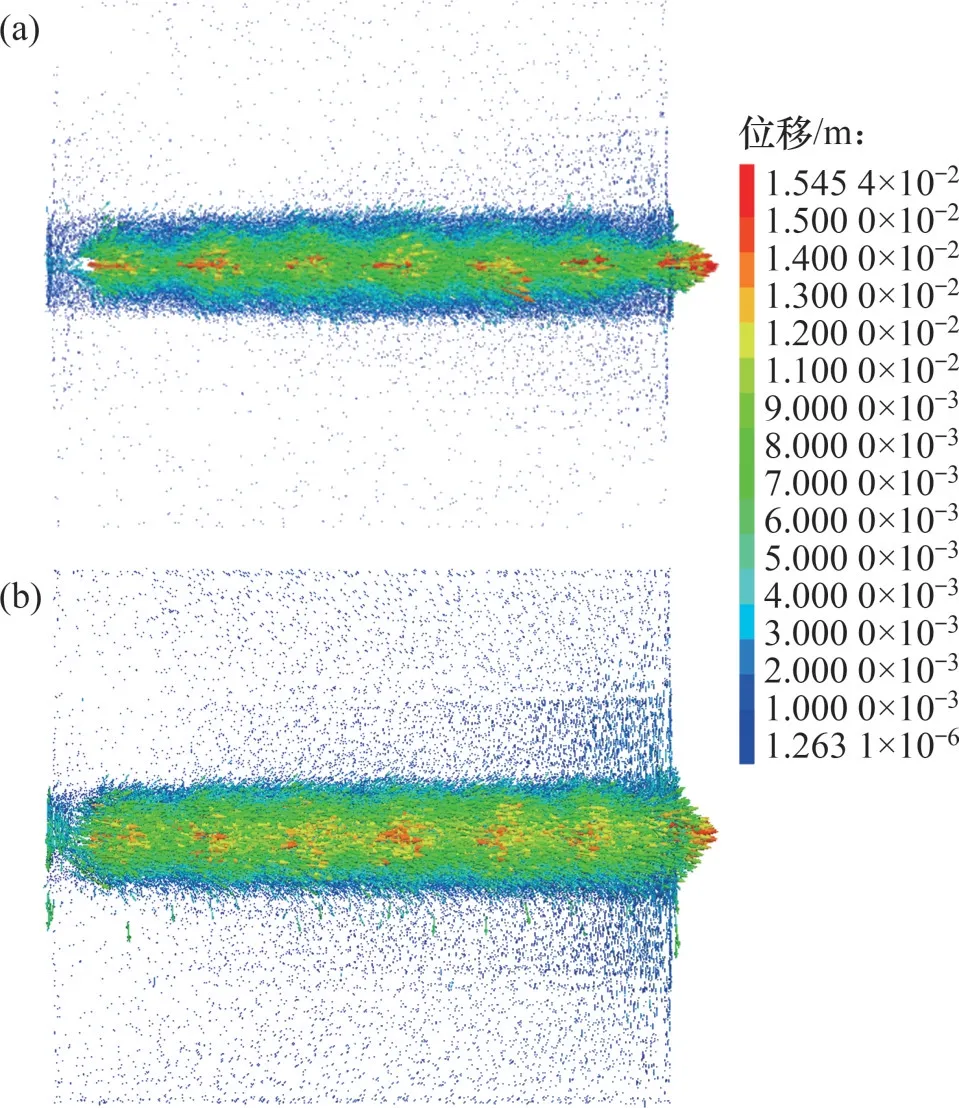
圖20 風積沙顆粒位移矢量圖Fig.20 Displacement vectors of aeolian sand particles

以上僅對2種工況風積沙顆粒的位移情況進行了簡單的定性分析，不能評價多種工況下格柵的立體加筋效果。對不同高度層次風積沙的水平位移均值進行統計，以定量分析不同厚度加強節點對剪切帶范圍的影響見圖21，其中，每層統計高度為10 mm。由圖21可知：當離開筋土界面一定范圍時，風積沙顆粒水平位移均值為負值，說明這些層次的大多數顆粒往后運動。不同工況下剪切帶的范圍和最大水平位移均值見表10。以1 mm的水平位移均值為界，土工格柵拔出15 mm后，工況A、C、E、F、G的剪切帶整體厚度分別為36.36、39.37、41.35、44.59和47.67 mm。相比于普通格柵，工況C、E、F、G的4種加強節點格柵的剪切帶范圍分別拓寬為原來的1.08、1.14、1.23、1.31倍，最大水平位移均值增大為原來的1.16、1.27、1.35、1.44倍。這說明加強節點一方面拓寬了剪切帶的影響范圍，使格柵具有立體加筋的效果，另一方面加強了格柵限制土體移動的能力。隨著節點厚度增大，剪切帶的分布范圍越大，最大水平位移均值增大。

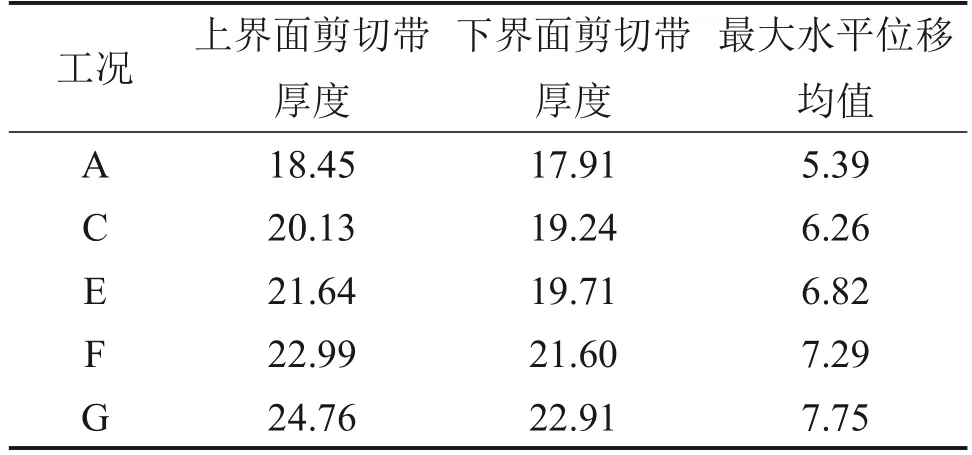
表10 不同工況下剪切帶的厚度范圍和最大水平位移均值Table 10 Thickness range and the maximum horizontal displacement of shear bands under different conditions mm

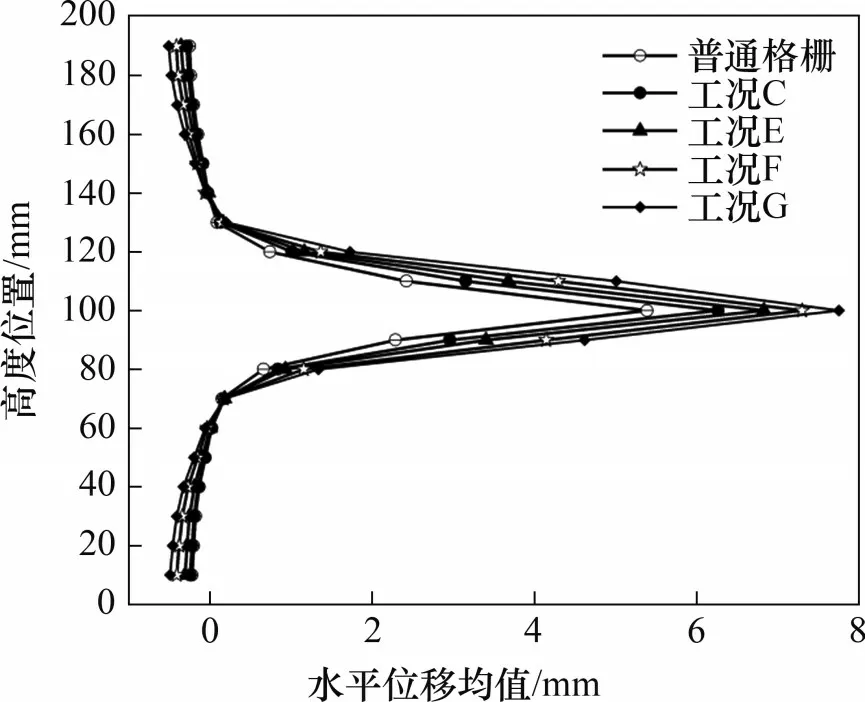
圖21 不同高度位置顆粒的水平位移均值Fig.21 Average horizontal displacement of particles at different heights

3.8 節點群體效應

為探究節點數量與極限拉拔阻力增量的關系(法向壓力為30 kPa)，以工況C加強節點土工格柵為基準，隨機刪除加強節點，改變加強節點的數量，得到圖22，圖中紅色圓代表加強節點。隨機分布下不同加強節點數量的拉拔力-拉拔位移曲線見圖23。從圖23可以看出：當加強節點隨機分布時，加強節點數量越多，前期拉拔力-拉拔位移曲線的斜率越大，節點提供的極限拉拔阻力增量越大。同樣以工況C的加強節點土工格柵為基準，只保留某一排加強節點，節點數量固定為10個。假定橫肋上的加強節點互相不影響，在這種規則分布下，每個節點可視為單獨工作。在30 kPa法向壓力下得到多組拉拔結果，如表11所示。表11中的7條橫肋均埋在有效區域內，具體可見圖4(b)。加強節點提供的極限拉拔阻力增量最小值為31.6 N，最大值為60.9 N。不同空間位置的加強節點所提供的極限拉拔阻力增量不同，說明筋土界面的剪應力分布不均勻。

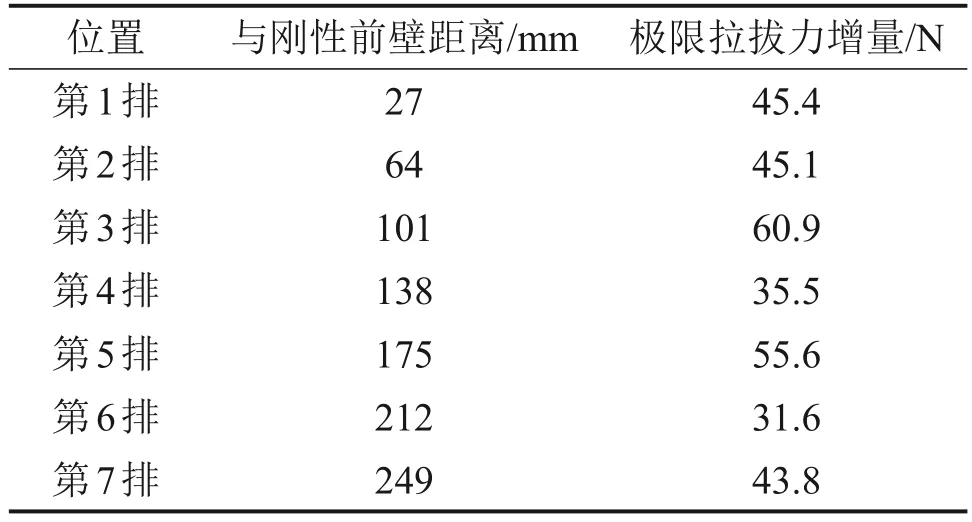
表11 規則分布下節點的極限拉拔阻力增量Table 11 Ultimate pull-out resistance increment of nodes under regular distribution

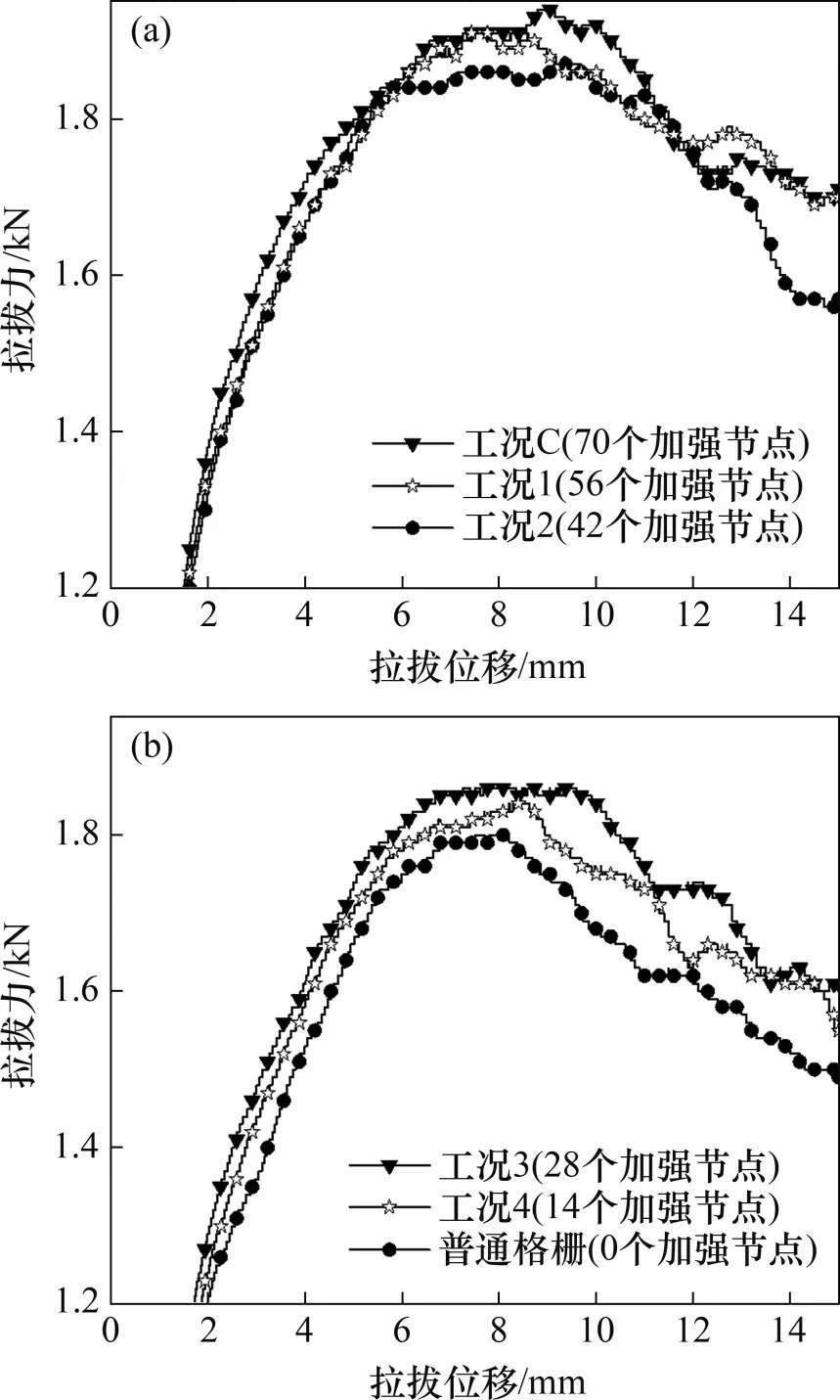
圖23 隨機分布下不同加強節點數量的拉拔結果Fig.23 Pull-out results with different numbers of strengthened nodes under random distribution

不同分布情況下節點數量-極限拉拔阻力增量的關系見圖24。從圖24可見：在隨機分布下，節點數量與極限拉拔阻力增量表現出良好的線性關系，得出線性擬合式T=1.961 0N(其中，T為極限拉拔阻力增量，N為加強節點數量)，擬合優度為0.991 7。依據表11中數據，將每排加強節點提供的極限拉拔阻力增量相加，可得到圖24中節點規則分布時的節點數量-極限拉拔阻力增量的關系。曲線采用線性擬合，T=4.464 9N，擬合優度為0.998 5。可以看出，在節點數量相同時，節點規則分布時的極限拉拔阻力增量之和大于隨機分布時的極限拉拔阻力增量，證明多個節點同時工作時存在一種群體效應，導致單位數量節點對極限拉拔阻力的提高率降低。2個節點的滑裂面示意圖如圖25所示，縱肋上2個相鄰節點的影響區域相互重疊，導致2個節點同時存在時的影響區域面積小于節點單獨存在時影響區域面積之和，產生了顯著的群體效應，單位數量節點對極限拉拔阻力的提高率降低。節點群體效應解釋了圖11所示的規律，當材料一定時，相比于單側布置節點，上下兩側同時加強的方式，減小了重疊區域占影響區域的比例，在一定程度上減弱了節點的群體效應。

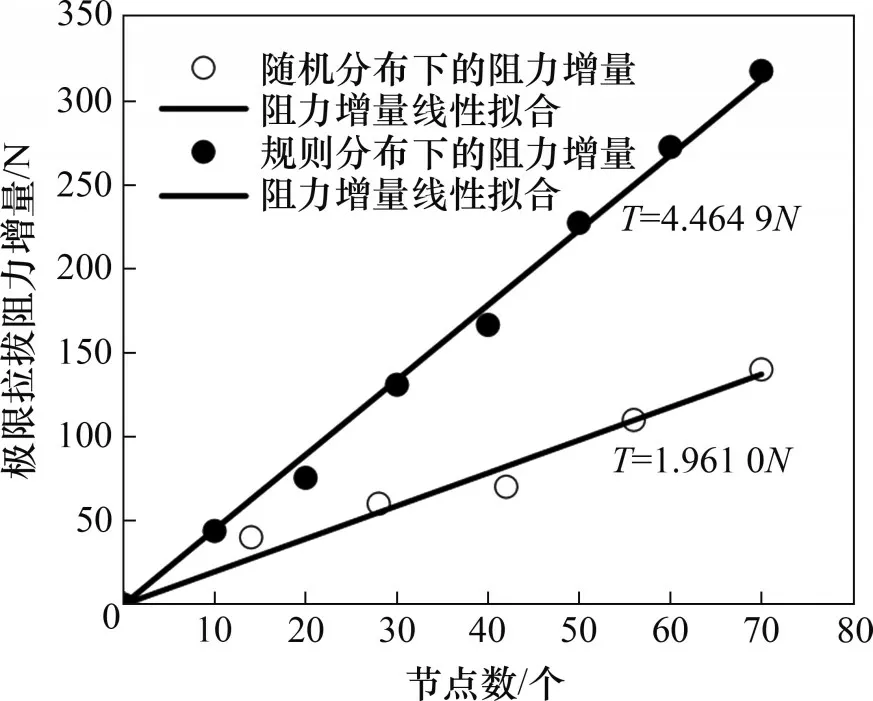
圖24 節點數量-極限拉拔阻力增量的關系Fig.24 Relationship between number of nodes and ultimate pull-out resistance increment

圖25 2個節點的滑裂面示意圖Fig.25 Diagram of slip fracture surface of two nodes

當2個相鄰節點的間距太小時，這2個節點的影響區域互相重疊，產生顯著的群體效應。若增大相鄰節點間距，則會存在一個臨界點，使相鄰節點互不影響。不同節點間距的4種設計工況見圖26。節點群體效應折減系數η為評價群體效應強弱程度的量化指標，可通過下式計算：

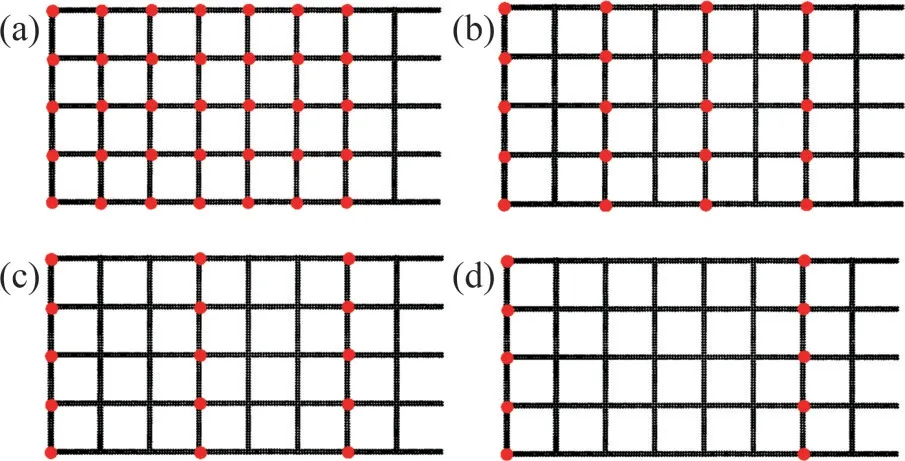
圖26 不同節點間距的設計工況Fig.26 Design conditions of different node spacings

式中：tr為節點任意分布時單位數量節點提供的極限拉拔阻力增量；ts為節點單獨存在時提供的極限拉拔阻力增量。不同工況下的群體效應折減系數見表12，群體效應折減系數與相鄰節點間距的關系見圖27。由圖27可知：隨著節點間距增大，相鄰節點重疊的影響區域變小，群體效應折減系數逐漸減小，節點的群體效應減弱。對群體效應折減系數進行多項式擬合，得出擬合式如下：

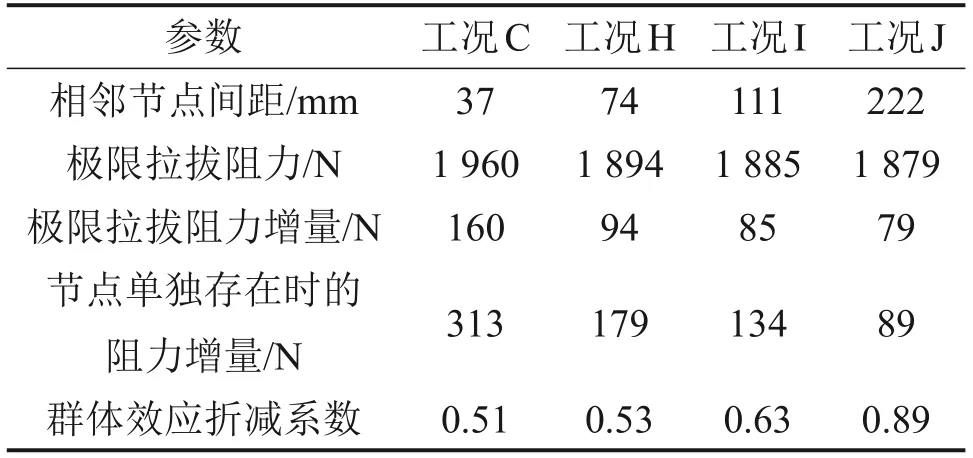
表12 不同工況下的群體效應折減系數Table 12 Reduction coefficient of group effect under different conditions

擬合優度為0.975 0，依據多項式擬合式可以預測最優的節點間距。當η為1時，得出相鄰節點間距為255 mm，說明當相鄰節點間距超過255 mm時，相鄰節點的影響范圍不再重疊，多節點同時存在時提供的極限拉拔阻力增量不會折減。

4 結論

1) 相比于均質風積沙數值模型，分層風積沙數值模型的模擬結果與室內試驗結果更接近，證明了分層風積沙數值模型計算拉拔阻力的合理性及優越性。依據刺入剪切理論計算節點得到的極限拉拔阻力增量與數值解接近，證明了節點模擬方法的合理性。

2) 當多個節點同時工作時，若相鄰節點間距太小，則節點的影響區相互重疊，產生節點群體效應，導致每個節點的效率降低。隨著相鄰節點間距增大，節點群體效應逐漸減弱。

3) 節點排布方式影響了格柵加筋性能。當節點厚度一定時，相比于單側布置節點，雙側布置節點的方式減小了重疊區域占影響區域的比例，削弱了節點群體效應。

4) 當布置方式固定時，隨節點厚度變大，節點提供的極限拉拔阻力增量變大。單位厚度節點提供的極限拉拔阻力基本不變，極限拉拔阻力增量與節點厚度增量呈良好的線性關系。

5) 格柵前段、中段、后段的峰值應變增量與節點厚度增量呈良好的線性關系，格柵前段峰值應變的增長速度為格柵中段的1.81倍，為格柵后段的2.83倍。

6) 與普通土工格柵相比，加強節點土工格柵對筋土界面的擾動更強烈，使試樣整體的剪脹趨勢更加顯著。相比于普通土工格柵，工況G中剪切帶的厚度拓寬為原來的1.31倍，發揮出明顯的立體加筋效果，最大水平位移均值增大為原來的1.44倍，其具有更強的限制土體位移的能力。