基于CEL方法的瓷磚智能化鋪貼質(zhì)量數(shù)值分析

吳楷，張艷榮，孔祥明，張浩楠，李大林，雷霆

(1.北京交通大學(xué) 土木建筑工程學(xué)院，北京，100044；2.清華大學(xué) 土木工程系，北京，100084)

在建筑工程中，瓷磚鋪貼是最適合應(yīng)用機(jī)器人技術(shù)的環(huán)節(jié)之一[1-4]，相關(guān)研究受到國(guó)內(nèi)外廣泛關(guān)注[5-11]。APOSTOLOPOULOS等[5]提出了可全方位移動(dòng)的地磚安裝機(jī)器人，搭載激光三角測(cè)量系統(tǒng)進(jìn)行導(dǎo)航和定位，并采用高分辨率攝像機(jī)評(píng)估安裝質(zhì)量。NAVON[6]利用圖形仿真系統(tǒng)研制了一款采用六自由度機(jī)械臂的地磚安裝機(jī)器人，并開發(fā)了一套電腦視覺系統(tǒng)實(shí)現(xiàn)瓷磚的高精度安裝和缺陷識(shí)別，其鋪貼效率是人工鋪貼的2～5倍。柳洪義等[7]研發(fā)的瓷磚機(jī)器人通過激光測(cè)距傳感器和測(cè)量程序檢測(cè)壁面與地表狀況，并精準(zhǔn)控制涂料厚度和瓷磚鋪貼位置，可以在10 s內(nèi)完成長(zhǎng)度×寬度為150 mm×150 mm瓷磚的鋪貼。劉侃[8]設(shè)計(jì)的導(dǎo)軌移動(dòng)式瓷磚鋪貼機(jī)器人集成了免光照影響的空間定位技術(shù)和多段路徑規(guī)劃的平滑鋪貼模式，較人工鋪貼縮短工時(shí)20.9%。LI等[9]提出了一種基于自適應(yīng)視覺的瓷磚機(jī)器人控制方案，實(shí)現(xiàn)了在無(wú)標(biāo)定攝像機(jī)和有限視野的情況下瓷磚的自動(dòng)拾取與鋪貼，極大提高了瓷磚機(jī)器人的自主能力。WANG等[10]提出了一種基于視覺測(cè)量的瓷磚位置補(bǔ)充算法，可對(duì)瓷磚的鋪貼質(zhì)量進(jìn)行在線評(píng)估。許世斌[11]設(shè)計(jì)了一款地磚自動(dòng)化涂漿機(jī)，可連續(xù)完成水泥漿攪拌和涂抹2個(gè)工序，節(jié)省近50%的時(shí)間并降低施工空鼓率至0.1%。既有文獻(xiàn)主要關(guān)注瓷磚鋪貼機(jī)器人中不同模塊的功能強(qiáng)化和一體化設(shè)計(jì)，但有關(guān)機(jī)器人施工工藝參數(shù)對(duì)瓷磚鋪貼質(zhì)量影響的研究較少。為此，本文建立瓷磚-瓷磚膠-混凝土流固耦合施工模型，針對(duì)機(jī)器人施工工藝參數(shù)對(duì)瓷磚鋪貼質(zhì)量的影響開展研究。

1 基本理論

拉格朗日法和歐拉法是連續(xù)介質(zhì)力學(xué)中用于描述材料運(yùn)動(dòng)的2種基本算法，其中，前者主要用于固體力學(xué)領(lǐng)域的有限元模擬，可準(zhǔn)確描述物體邊界運(yùn)動(dòng)，但在模擬大變形時(shí)易出現(xiàn)網(wǎng)格畸變而降低精度；后者主要用于流體力學(xué)領(lǐng)域，計(jì)算流體流動(dòng)等極端變形問題，但無(wú)法精確地捕捉物體的邊界信息[12]。這兩者均遵循質(zhì)量守恒定律、動(dòng)量守恒定律和能量守恒定律，分別采用物質(zhì)時(shí)間導(dǎo)數(shù)和空間時(shí)間導(dǎo)數(shù)的形式表達(dá)[13]，如表1所示。歐拉方程可統(tǒng)一成一般的守恒形式，如式(1)所示。NOH[12]提出了歐拉-拉格朗日方法(CEL方法)，該方法結(jié)合了這兩者的優(yōu)勢(shì)，可用于多組件復(fù)雜流固耦合結(jié)構(gòu)的模擬[14-16]，該方法將式(1)拆分成式(2)和式(3)。

表1 守恒方程Table 1 Conservative equations

式中：Φ為通量函數(shù)；S為源項(xiàng)。

2 模型建立

2.1 瓷磚膠屈服變形試驗(yàn)

首先，將直徑為60 mm、高度為20 mm的圓筒模具置于濕潤(rùn)的SiO2玻璃板(長(zhǎng)×寬×厚度為200 mm×200 mm×15 mm)中心；然后，將拌合均勻的德高TTB I型瓷磚膠(水膠比為6:25)倒入圓筒模具中并抹平，隨即垂直、平穩(wěn)地提起圓桶模具，將另一玻璃板(重0.2 N)水平置于瓷磚膠頂部，此時(shí)瓷磚膠未變形；最后，對(duì)玻璃板均勻施加2 N荷載；待瓷磚膠停止變形后記錄其底部直徑，如圖1所示。同樣，依次記錄荷載為4 N和6 N時(shí)瓷磚膠的底部直徑。

圖1 瓷磚膠屈服變形試驗(yàn)結(jié)果Fig.1 Experiment result of the yield deformation of tile adhesive

2.2 瓷磚膠屈服變形模型與驗(yàn)證

有研究指出，線性Drucker-Prager模型通過非圓形屈服面來(lái)反映不同的三軸拉伸和壓縮屈服強(qiáng)度、偏平面上的塑性流動(dòng)以及不同的剪脹角和摩擦角，可用于模擬新拌砂漿和混凝土[17-18]。線性Drucker-Prager模型主要由屈服面函數(shù)和流動(dòng)勢(shì)函數(shù)等構(gòu)成[19]，分別如式(4)和(5)所示。

式中：F為屈服面函數(shù)；為偏應(yīng)力；q為等效Mises應(yīng)力；k為三軸拉壓屈服應(yīng)力比；r為偏應(yīng)力第三不變量；p為等效壓應(yīng)力；β為s-p平面上屈服面的傾角，即材料的摩擦角；d為s-p平面上屈服面的截距，即材料的黏聚力；G為塑性流動(dòng)勢(shì)能；ψ為s-p平面上的剪脹角。

基于CEL方法，建立瓷磚膠屈服變形模型，如圖2所示。圖2中，從上到下依次為頂部玻璃板、瓷磚膠和底部玻璃板。采用剛體模擬玻璃板；采用歐拉域模擬瓷磚膠，其本構(gòu)方程為Drucker-Prager模型，物理和力學(xué)性能參數(shù)如表2所示。在頂部玻璃片上分別施加2、4和6 N的均布荷載，計(jì)算瓷磚膠的底部直徑。

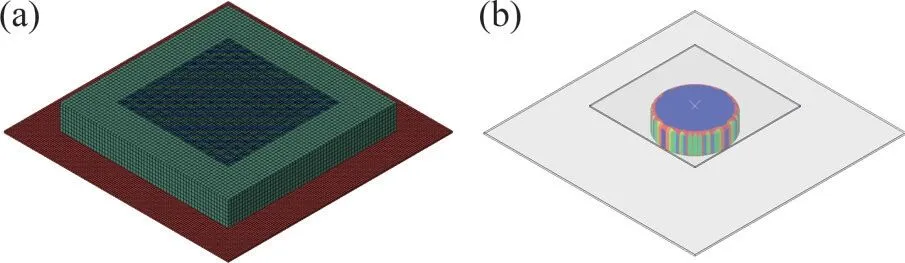
圖2 瓷磚膠屈服變形模型Fig.2 Model of the yield deformation of tile adhesive

表2 瓷磚膠的物理和力學(xué)參數(shù)Table 2 Physical and mechanical parameters of tile adhesive

圖3所示為瓷磚膠底部直徑的模擬結(jié)果與試驗(yàn)結(jié)果對(duì)比。由圖3可以看出，瓷磚膠底部直徑的模擬結(jié)果與試驗(yàn)結(jié)果基本一致，最大相對(duì)誤差僅為-1.98%，證明了本研究所用的CEL流固耦合模型的可靠性。

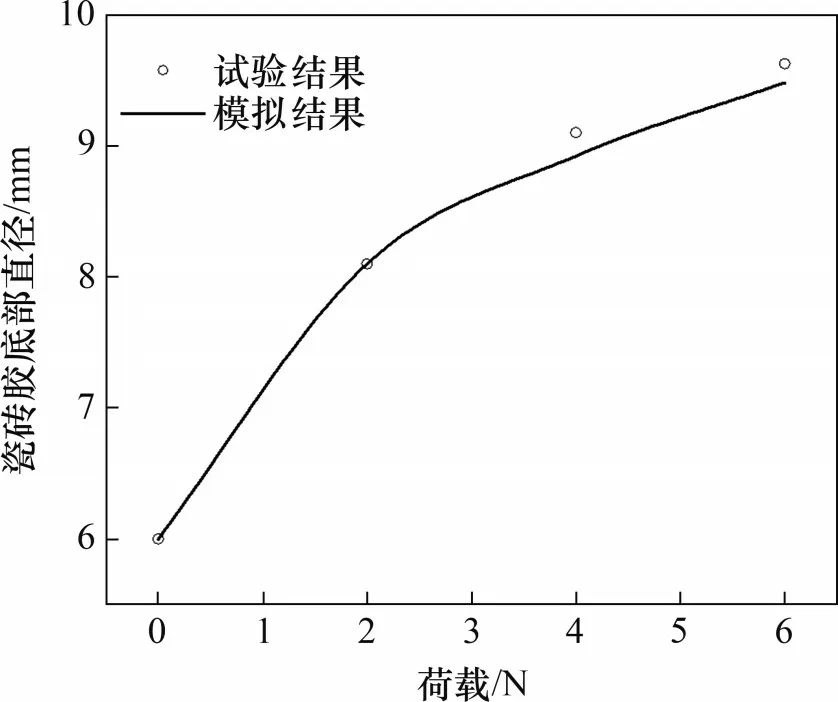
圖3 瓷磚膠底部直徑的模擬結(jié)果與試驗(yàn)結(jié)果對(duì)比Fig.3 Comparison between numerical and experimental results of the diameter of the bottom tile adhesive

2.3 瓷磚-瓷磚膠-混凝土流固耦合模型

參照文獻(xiàn)[20]中地磚鋪貼機(jī)器人(圖4)的工作模式，建立瓷磚-瓷磚膠-混凝土CEL施工模型，包括瓷磚膠布料和瓷磚調(diào)平2個(gè)子模型，如圖5所示。布料模型由歐拉域和混凝土基層組成，用于分析布料方式對(duì)瓷磚膠變形的影響；調(diào)平模型由瓷磚、歐拉域和混凝土基層組成，用于分析布料管數(shù)、荷載類型對(duì)瓷磚鋪貼質(zhì)量的影響。根據(jù)GB 50209—2010《建筑地面工程施工質(zhì)量驗(yàn)收規(guī)范》要求[21]，依次選取瓷磚回彈量、瓷磚-瓷磚膠接觸面積、瓷磚膠-混凝土基層接觸面積和缺陷分布等指標(biāo)表征瓷磚的鋪貼質(zhì)量。

圖4 地磚鋪貼機(jī)器人[20]Fig.4 Tiling robot[20]

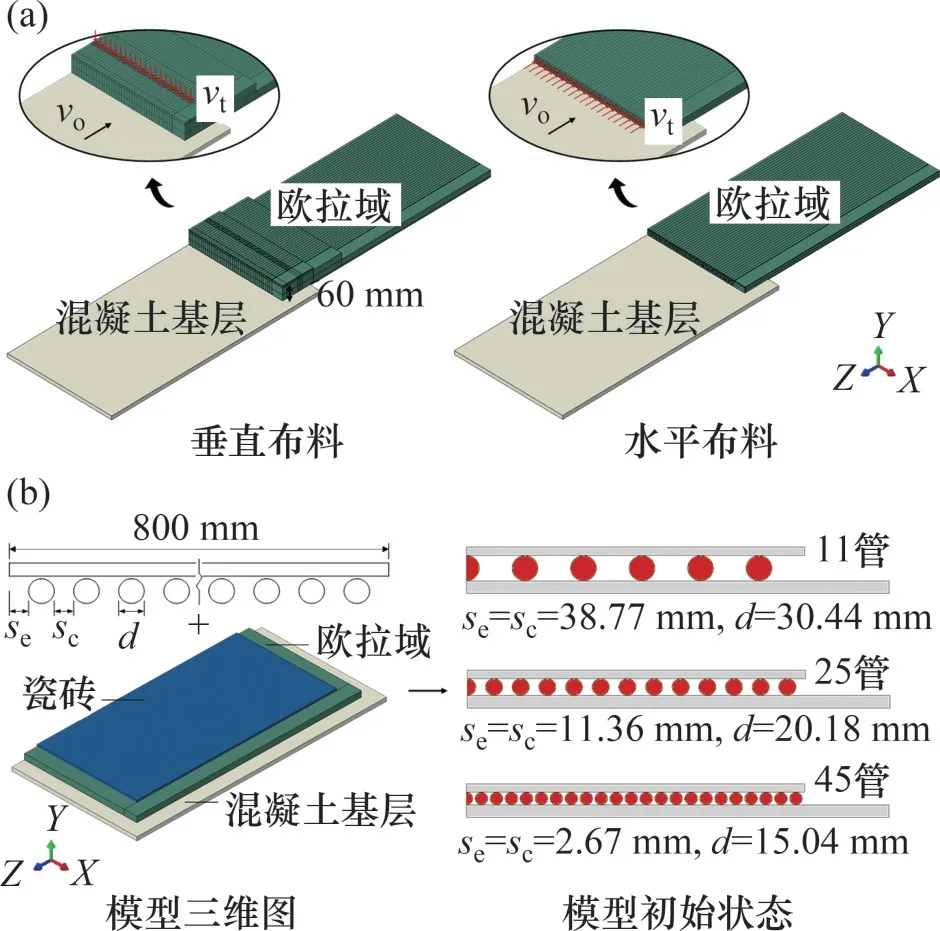
圖5 瓷磚-瓷磚膠-混凝土CEL施工模型Fig.5 CEL construction models of tile-adhesive-concrete

瓷磚和混凝土基層的長(zhǎng)×寬×厚度分別為0.8 m×0.8 m×0.01 m和1.0 m×1.0 m×0.015 m。瓷磚膠的設(shè)計(jì)體積取0.006 4 m3，并代入式(6)計(jì)算出漿口的尺寸。由于機(jī)器人采用連續(xù)方式布置瓷磚膠，布料模型中瓷磚膠的長(zhǎng)度取0.8 m(以布料1塊瓷磚的長(zhǎng)度為例)，調(diào)平模型中瓷磚膠的長(zhǎng)度取0.9 m(考慮相鄰瓷磚膠的影響)。歐拉域體積滿足覆蓋瓷磚膠變形區(qū)域的要求即可。

式中：n為布料管數(shù)；V為瓷磚膠設(shè)計(jì)體積。

瓷磚和混凝土基層均模擬為剛體，分別由11萬(wàn)個(gè)和17萬(wàn)個(gè)實(shí)體單元組成。瓷磚膠設(shè)為歐拉體，對(duì)應(yīng)的歐拉域分別由250萬(wàn)個(gè)(布料模型)和590萬(wàn)個(gè)(調(diào)平模型)歐拉單元組成。以“硬”接觸和“罰”接觸(摩擦因數(shù)為1)模擬瓷磚膠與瓷磚、瓷磚膠與混凝土基層間的法向和切向相互作用。瓷磚和混凝土的密度分別為2 400 kg/m3和2 300 kg/m3，瓷磚膠的材料參數(shù)如表2所示。

布料模型中瓷磚膠的布料管數(shù)為40根，如圖5(a)所示。出漿口的移動(dòng)速度和瓷磚膠的出漿速度均設(shè)置為0.25 m/s，但兩者方向相反。調(diào)平模型中，瓷磚膠的布料管數(shù)取11、25和45根，如圖5(b)所示。混凝土基層設(shè)置固結(jié)約束，瓷磚膠縱向兩端設(shè)置對(duì)稱約束。在瓷磚頂面施加3種位移調(diào)平荷載(圖6)：直壓荷載(下壓至瓷磚膠的厚度為10 mm，加載2 s，簡(jiǎn)稱為VC模式)、先直壓荷載(10 mm，加載2 s)后垂直振動(dòng)荷載(0.025 mm，40 Hz，持續(xù)5 s，簡(jiǎn)稱為VV模式)、先直壓荷載(10 mm，加載2 s)后剪切振動(dòng)荷載(0.025 mm，40 Hz，持續(xù)5 s，簡(jiǎn)稱為SV模式)。為提高計(jì)算效率，上述模型均為半模型，在對(duì)稱面設(shè)置對(duì)稱約束。計(jì)算時(shí)所有模型均施加重力均布荷載。

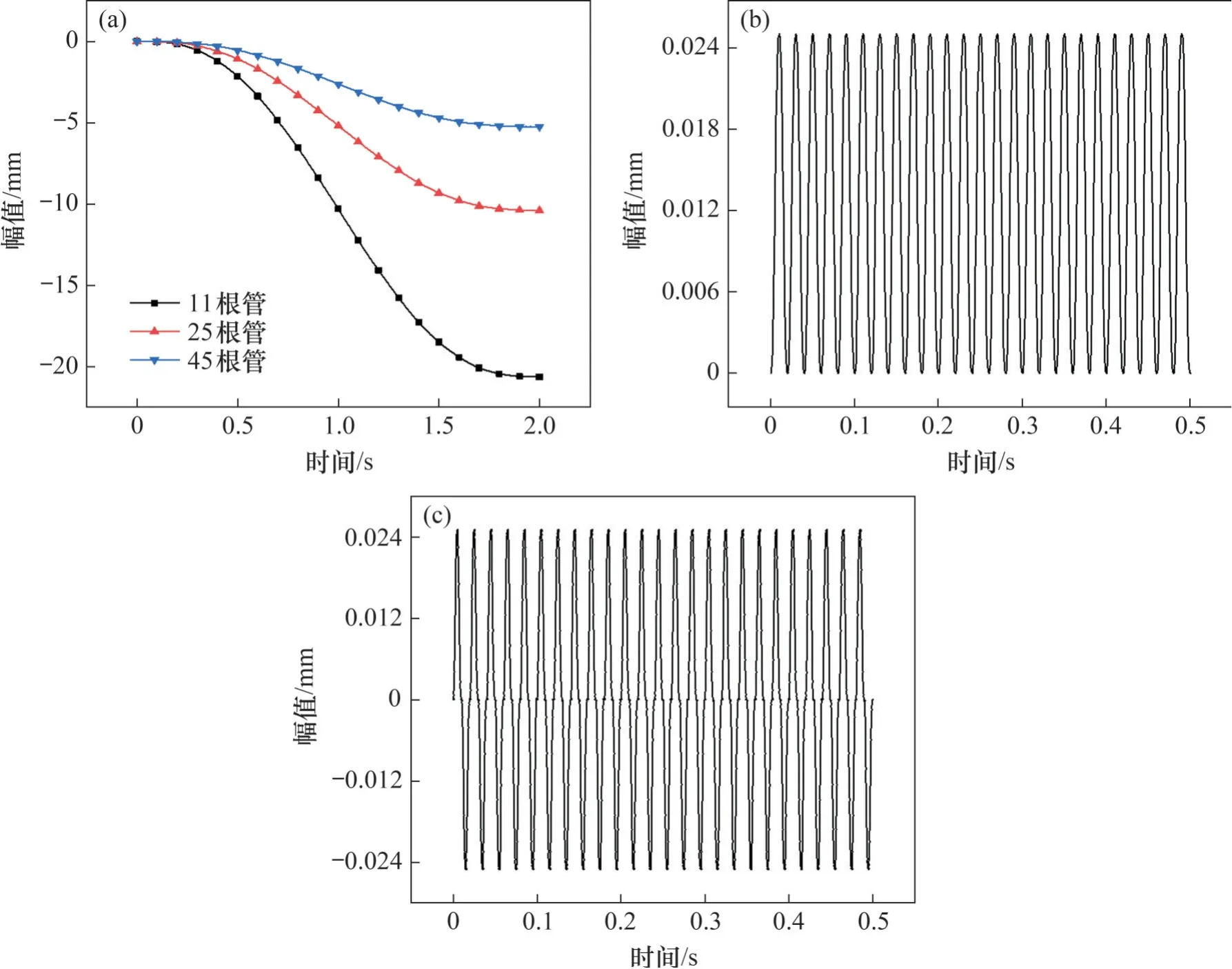
圖6 荷載幅值曲線Fig.6 Amplitude curves of loads

3 結(jié)果與討論

3.1 布料方式的影響

圖7所示為水平和垂直布料方式下瓷磚膠的塑性應(yīng)變?cè)茍D。由圖7可看出，采用水平布料時(shí)，瓷磚膠基本保持穩(wěn)定的擬圓柱態(tài)，呈等間距分布，塑性應(yīng)變幾乎為0；采用垂直布料時(shí)，瓷磚膠與基層接觸后發(fā)生彎折，塑性應(yīng)變高達(dá)0.75；瓷磚膠的形態(tài)發(fā)生明顯改變，多坍塌為半圓柱狀，瓷磚膠間距縮小。

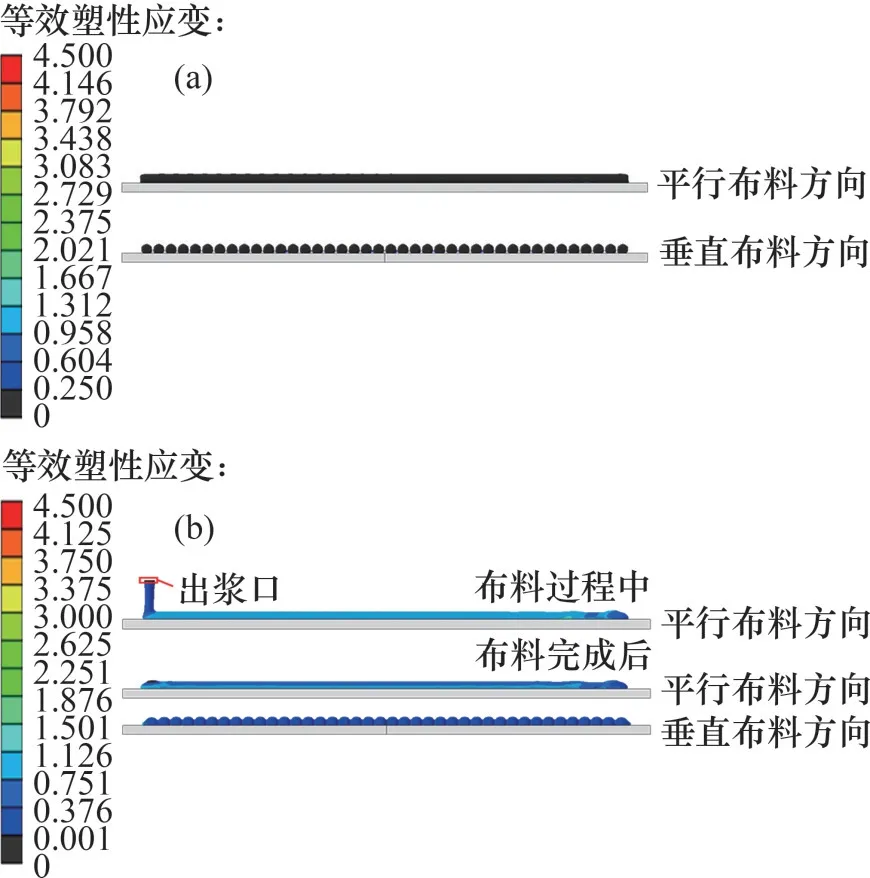
圖7 水平和垂直布料方式下瓷磚膠等效塑性應(yīng)變?cè)茍DFig.7 Contour plots of the equivalent plastic strains of tile adhesive applied horizontally and vertically

在瓷磚膠布料過程中，其塑性應(yīng)變主要取決于材料的屈服應(yīng)力、重力以及基層摩阻力等。垂直布料時(shí)，瓷磚膠接觸基層前即在重力作用下產(chǎn)生一定量的屈服變形(圖7(b))，接觸基層后動(dòng)能轉(zhuǎn)變?yōu)樗苄宰冃文埽纱u膠形態(tài)相應(yīng)發(fā)生較大改變(坍塌)，瓷磚膠間距縮小。而采用水平布料時(shí)，瓷磚膠的重力與基層支撐力相抵，瓷磚膠與基層相對(duì)靜止(出漿口移動(dòng)速度與瓷磚膠的出漿速度大小相等但方向相反)，輕小的基層摩阻力不足以引起瓷磚膠屈服變形。因此，在整個(gè)水平布料過程中，瓷磚膠基本保持原形態(tài)不變。

此外，水平布料后的瓷磚膠體積為0.006 4 m3，即與設(shè)計(jì)體積(0.8 m×0.8 m×0.01 m)相等；而垂直布料后的瓷磚膠體積僅為0.006 26 m3，這主要是瓷磚膠出漿速度與出漿口移動(dòng)速度不匹配所致。

3.2 布料管數(shù)的影響(水平布料，直壓荷載)

3.2.1 豎向位移與豎向力

在直壓加載(VC模式)過程中，不同布料管數(shù)時(shí)瓷磚豎向位移和豎向力隨時(shí)間的變化如圖8所示。圖8中，豎向位移為負(fù)表明瓷磚下移，豎向力為正代表瓷磚受拉，負(fù)值代表受壓。按照?qǐng)D6所示的直壓加載模式，瓷磚豎向位移在2 s內(nèi)逐漸增加至目標(biāo)位移D1并保持穩(wěn)定；卸載后位移輕微波動(dòng)，隨后保持穩(wěn)定位移D2。相應(yīng)地，瓷磚由受拉逐漸轉(zhuǎn)變?yōu)槭軌海覊毫徛龃螅Q向位移增至Ds時(shí)壓力迅速增加并逐漸保持為穩(wěn)定值Pm；卸載后瓷磚豎向力立即恢復(fù)至0 N。隨布料管數(shù)增加，瓷磚壓力急劇增大的時(shí)間點(diǎn)Ts明顯縮短，而D1與D2的差值以及最大瓷磚壓力Pm基本不受影響，分別為0.165 mm和3.40 kN。

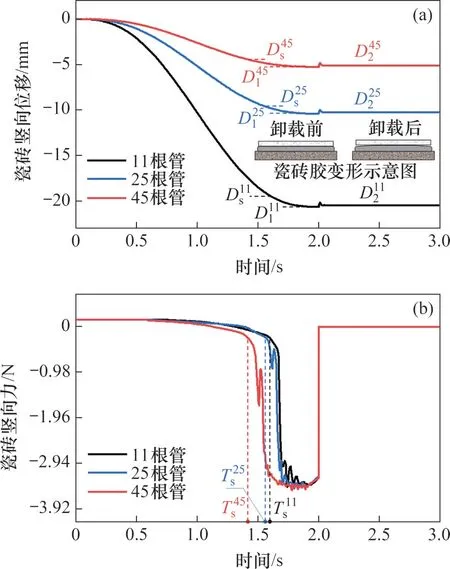
圖8 不同布料管數(shù)時(shí)瓷磚的豎向位移和豎向力隨時(shí)間的變化Fig.8 Variations of the vertical displacement and vertical force of tile with time under various rows of adhesive extrusion

眾所周知，在直壓加載過程中，瓷磚的豎向位移與瓷磚膠的豎向變形量相等。瓷磚膠在外力作用下發(fā)生彈性變形和塑性變形(對(duì)應(yīng)D1)；外力卸載后彈性變形立即恢復(fù)，僅殘留塑性變形(對(duì)應(yīng)D2)，D1與D2之差即為瓷磚膠的豎向回彈變形量。瓷磚膠的回彈量屬于材料本身特性參數(shù)，與布料管數(shù)無(wú)關(guān)。

調(diào)平瓷磚所施加的外力(豎向力)等于瓷磚膠的反彈力與瓷磚重力之差。在初始時(shí)刻，瓷磚膠的反彈力為0 N，瓷磚豎向力等于瓷磚重力(150 N)，此時(shí)瓷磚受拉；在調(diào)平過程中，隨著瓷磚豎向位移增加，瓷磚膠壓縮變形逐漸增大，反彈力相應(yīng)提高，瓷磚開始受壓；當(dāng)瓷磚豎向位移下壓至Ds時(shí)，瓷磚膠條之間開始接觸，瓷磚膠的壓縮變形受限，反彈力急劇增大；當(dāng)瓷磚膠間隙接近0 mm時(shí)，反彈力達(dá)到最大，此時(shí)，瓷磚豎向壓力達(dá)到最大值Pm。由圖5可知，布料管數(shù)越多，瓷磚膠條的間距越小；這意味著在壓縮變形過程中，瓷磚膠條之間越早接觸。因此，瓷磚壓力急劇增長(zhǎng)的時(shí)間點(diǎn)Ts隨布料管數(shù)增加而明顯提前。瓷磚膠的最大反彈力源于其自身的彈性變形，與布料管數(shù)無(wú)關(guān)，所以，瓷磚的Pm幾乎不受布料管數(shù)影響。

3.2.2 接觸面積

不同布料管數(shù)時(shí)瓷磚膠與瓷磚的接觸面積S1及其與基層的接觸面積S2隨時(shí)間的變化如圖9所示。在直壓加載過程中，不同布料管數(shù)的接觸面積S1均從0 m2逐漸增大至約0.64 m2，卸載后S1瞬間降低至0 m2而后迅速恢復(fù)至0.29 m2左右；接觸面積S2從不同的初始值逐漸增大至約0.64 m2，卸載后S2急劇下降隨后恢復(fù)至0.63 m2左右。

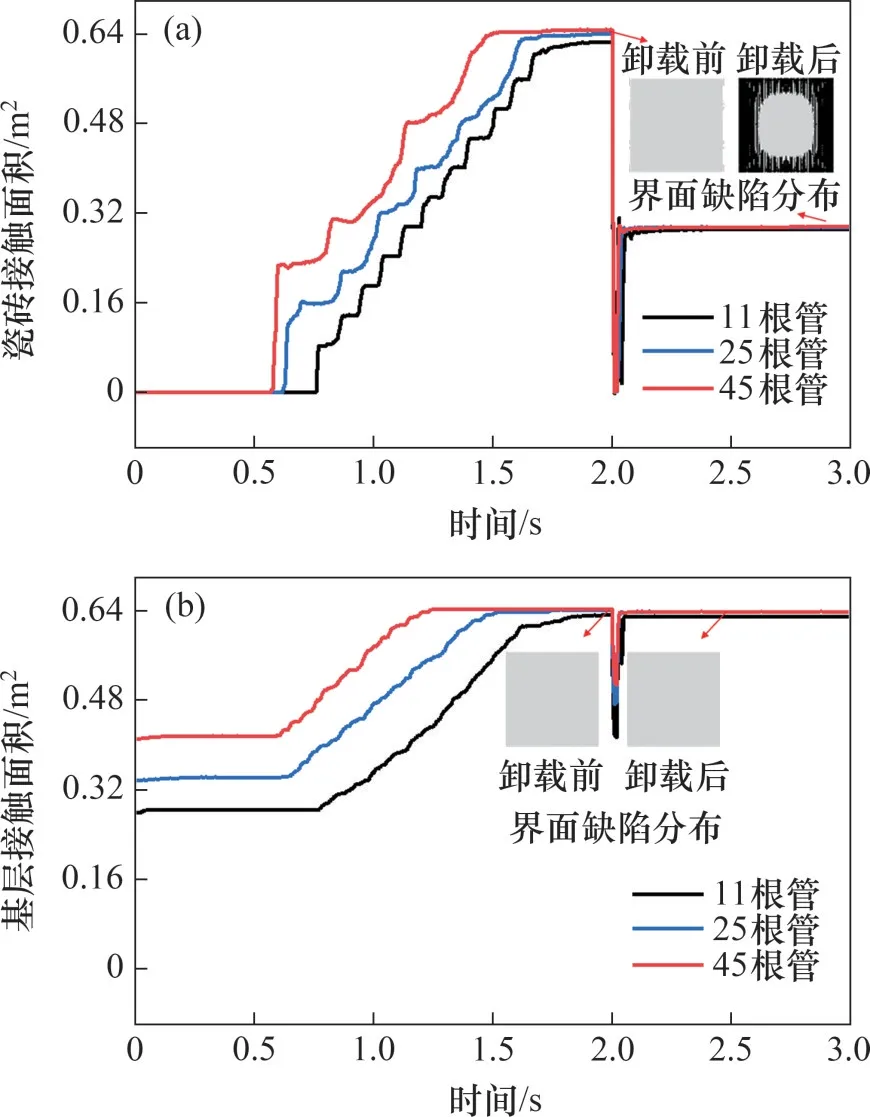
圖9 瓷磚膠與瓷磚和基層的接觸面積隨時(shí)間的變化Fig.9 Variations of the tile-adhesive contact area and adhesive-concrete base contact area with time

接觸面積的變化主要取決于瓷磚膠的初始形態(tài)以及直壓過程中的變形情況。在初始時(shí)刻，瓷磚未與瓷磚膠接觸，接觸面積S1為0 m2；布料管數(shù)越多，瓷磚膠條的間距越小，則接觸面積S2越大；在加載過程中，瓷磚膠變形逐漸增大，接觸面積隨之增加直至瓷磚膠條間隙接近0 mm，滿漿率幾乎達(dá)到100%；卸載后瓷磚膠回彈導(dǎo)致其與瓷磚完全脫離，接觸面積S1降為0 m2，S2急劇下降；瓷磚在重力作用下回落后接觸面積回升并保持穩(wěn)定。由于回落量小于回彈量，接觸面積S1的穩(wěn)定值遠(yuǎn)小于其最大值；而回彈變形主要發(fā)生在變形受限的頂部瓷磚膠(如圖8(a)所示)，底部瓷磚膠的回彈變形較小，因此，接觸面積S2的穩(wěn)定值與其最大值較接近。

此外，瓷磚膠的最終變形情況由材料的應(yīng)力應(yīng)變特性所決定，與布料管數(shù)無(wú)關(guān)。因此，最終的接觸面積S1和S2幾乎均不受布料管數(shù)的影響。

圖10所示為布料管數(shù)分別為11、25和45根時(shí)瓷磚-瓷磚膠界面缺陷的分布云圖。由圖10可知，瓷磚與瓷磚膠的脫空缺陷主要集中在瓷磚邊緣處，平行于布料方向。這主要是由于在直壓作用下瓷磚膠在約束較低的邊緣處產(chǎn)生了較大的塑性變形，外力卸載后瓷磚膠無(wú)法恢復(fù)形變導(dǎo)致在邊緣處出現(xiàn)了明顯的脫空。此外，盡管缺陷面積(對(duì)應(yīng)接觸面積)與布料管數(shù)無(wú)關(guān)，但是隨著布料管數(shù)的增加，瓷磚膠條間隙縮短引起脫空條紋明顯變窄且分布更加均勻，這有利于延緩硬化后瓷磚空鼓的進(jìn)一步發(fā)展[22-23]。

圖10 不同布料管數(shù)時(shí)瓷磚-瓷磚膠界面缺陷的分布云圖Fig.10 Contour plots of the distribution of tile-adhesive interfacial defect under various rows of adhesive extrusion

3.3 荷載類型的影響(水平布料，管數(shù)為45根)

3.3.1 直壓-垂直振動(dòng)荷載(VC-VV模式)

圖11(a)所示為VC-VV加載模式下瓷磚豎向位移和豎向力隨時(shí)間的變化。在前2 s的直壓過程中瓷磚豎向力與位移的變化規(guī)律與圖8中的一致，達(dá)到目標(biāo)位移D1(5.245 mm)時(shí)豎向力達(dá)到最大值Pm(3.40 kN)；之后施加垂直振動(dòng)荷載，豎向位移以0.025 mm的幅值波動(dòng)，豎向力與之同步呈波動(dòng)變化，在位移向下時(shí)達(dá)到最高，向上時(shí)降至最低；隨著作用時(shí)間的增加，豎向力的最大值和最小值均不斷減小。卸載后，豎向位移輕微波動(dòng)，隨后保持穩(wěn)定位移D2(5.142 mm)；豎向力由1.66 kN降至0 kN。

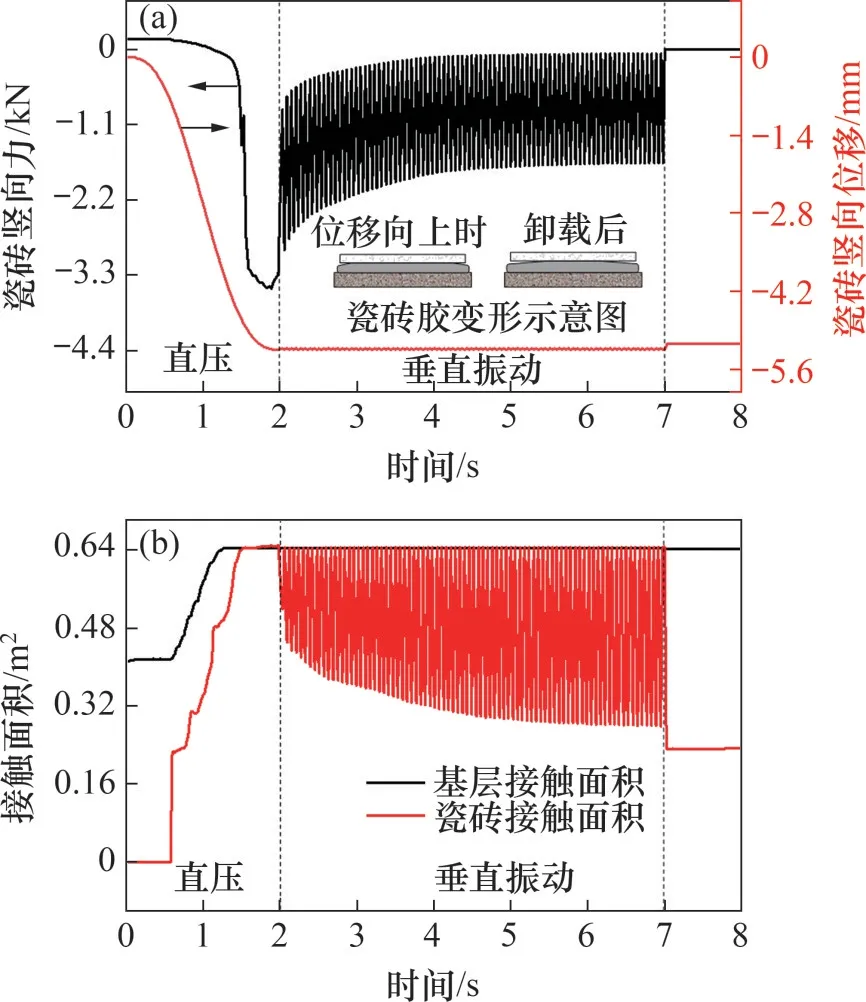
圖11 直壓-垂直振動(dòng)時(shí)瓷磚豎向位移和豎向力以及接觸面積隨時(shí)間的變化Fig.11 Variations of vertical displacement and force of tile and contact areas with time when loading the vertical vibration with compression

如前所述，調(diào)平瓷磚所施加的外力(豎向力)與瓷磚膠的反彈力即瓷磚膠的彈性變形呈正相關(guān)。下壓時(shí)，彈性變形增加，反彈力增大；上移時(shí)，恢復(fù)部分彈性變形，反彈力降低。新拌瓷磚膠作為一種典型的水泥基材料，在動(dòng)荷載下呈現(xiàn)顯著的黏彈塑性[24-25]，即隨著振動(dòng)加載時(shí)間的增加，瓷磚膠的塑性變形增加，彈性變形占比減小，瓷磚反彈力逐漸降低。外力卸載后，瓷磚膠的彈性變形完全恢復(fù)，僅殘留塑性變形，D1與D2之差(0.103 mm)即為瓷磚膠的豎向回彈變形量。

在直壓-垂直振動(dòng)耦合荷載作用下瓷磚膠與瓷磚接觸面積S1以及瓷磚膠與基層接觸面積S2的演化過程如圖11(b)所示。從圖11(b)可以看出，接觸面積S1和S2均在直壓作用下達(dá)到0.640 m2；施加垂直振動(dòng)荷載后，接觸面積S2保持穩(wěn)定，S1與豎向位移同步呈波動(dòng)變化，在瓷磚下壓時(shí)達(dá)到最高，上移時(shí)降至最低；隨著作用時(shí)間的增加，S1的波峰保持為0.640 m2，波谷不斷減小；卸載后，S1降至0.232 m2，S2保持為0.640 m2。

接觸面積S1的變化主要源于垂直振動(dòng)過程中瓷磚膠的不均勻變形。具體來(lái)講，當(dāng)瓷磚下壓至0.025 mm時(shí)，瓷磚膠壓縮變形增大，接觸面積S1隨之增加；瓷磚上移0.025 mm時(shí)，部分彈性變形恢復(fù)，瓷磚與瓷磚膠的接觸面積相應(yīng)減小。隨著振動(dòng)加載時(shí)間的增加，瓷磚膠的塑性變形增大，尤其在約束較低的邊緣處產(chǎn)生較大的塑性變形，致使瓷磚膠呈現(xiàn)中心飽滿、邊緣塌陷的狀態(tài)(圖11(a))，從而導(dǎo)致上移時(shí)與瓷磚的接觸面積降低；外力卸載后，中心瓷磚膠的彈性變形完全恢復(fù)，瓷磚膠在中心與邊緣的不均勻變形加劇(圖11(a))，最終導(dǎo)致接觸面積S1明顯降低。

此外，由3.2.2節(jié)可知，與頂部瓷磚膠相比，底部瓷磚膠的回彈變形較小，對(duì)接觸面積S2影響較小。垂直振動(dòng)加載和卸載后，底部瓷磚膠的塑性變形增大，回彈變形的影響進(jìn)一步減小。因此，瓷磚膠與基層的接觸面積S2在加載過程中以及卸載后始終保持不變。

3.3.2 直壓-剪切振動(dòng)荷載(VC-SV模式)

在VC-SV加載模式下瓷磚豎向位移、豎向力以及接觸面積隨時(shí)間的變化如圖12所示。顯然，在施加剪切振動(dòng)荷載后，豎向位移保持不變；豎向壓力逐漸減小，在5.52 s時(shí)壓力轉(zhuǎn)變?yōu)槔χ饾u增大直至保持穩(wěn)定。卸載后，豎向位移保持穩(wěn)定，無(wú)回彈；豎向力由45 N瞬間降至0 N。接觸面積S1和S2在剪切振動(dòng)作用時(shí)和卸載后基本保持為0.640 m2。

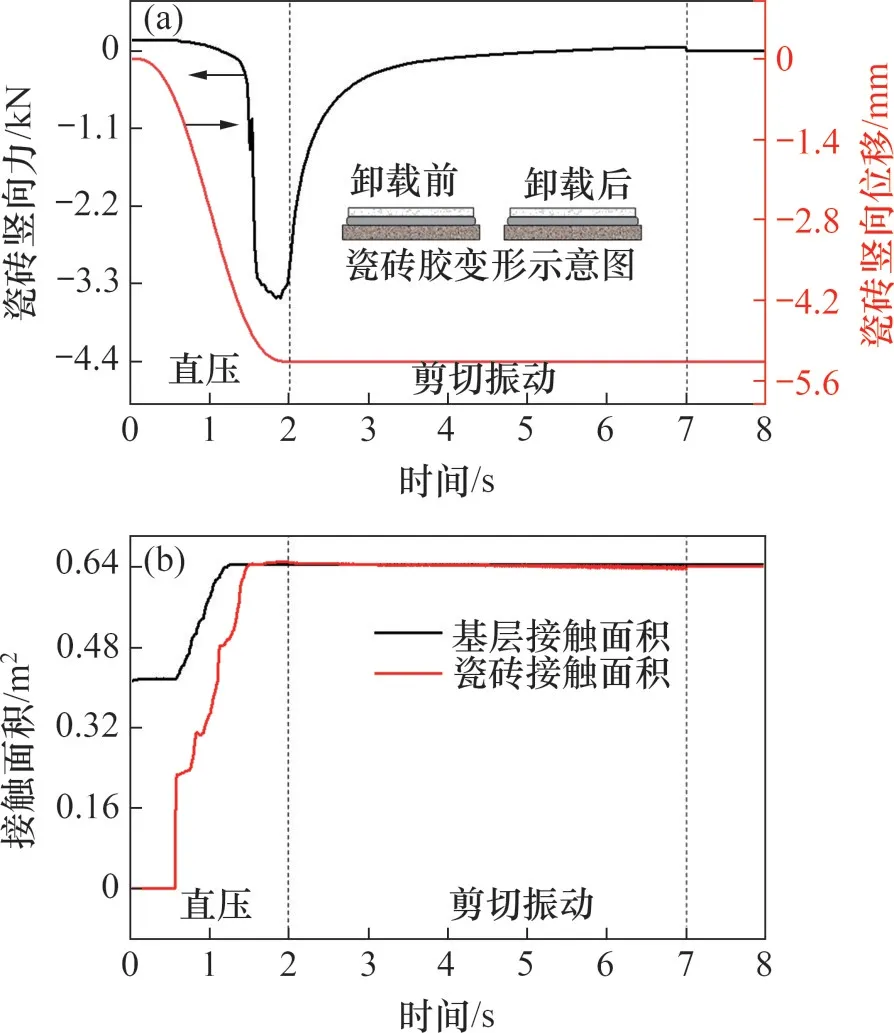
圖12 直壓-剪切振動(dòng)時(shí)瓷磚豎向位移和豎向力以及接觸面積隨時(shí)間的變化Fig.12 Variations of vertical displacement and force of tile and contact areas with time when loading the shear vibration with compression

上述現(xiàn)象表明，瓷磚膠在剪切振動(dòng)作用下主要發(fā)生塑性變形，彈性變形占比隨著加載時(shí)間的延長(zhǎng)逐漸降低、反彈力下降，導(dǎo)致瓷磚豎向力相應(yīng)減小；當(dāng)瓷磚膠的反彈力不足以抵抗瓷磚重力時(shí)，瓷磚豎向力由壓力轉(zhuǎn)變?yōu)槔ΑＰ遁d后瓷磚膠在瓷磚重力作用下難以發(fā)生屈服變形，瓷磚豎向位移基本保持不變。此外，由于在剪切振動(dòng)加載和卸載后，瓷磚膠始終發(fā)生均勻變形，因此，接觸面積S1和S2始終保持不變。

3.3.3 不同加載模式對(duì)比

不同類型荷載作用時(shí)瓷磚的鋪貼質(zhì)量如圖13所示。從圖13可見：相較于單一的直壓荷載，耦合垂直振動(dòng)后，瓷磚回彈量降低了37.58%，接觸面積S1減小了21.62%，接觸面積S2增大0.31%；耦合剪切振動(dòng)導(dǎo)致瓷磚回彈完全消失，接觸面積S1增大了116.22%，接觸面積S2增大0.31%。這表明，振動(dòng)荷載的引入可以有效地減小瓷磚膠彈性變形的影響，從而降低瓷磚回彈量，有利于增加瓷磚的初始平順性；然而，垂直振動(dòng)荷載會(huì)同時(shí)引發(fā)瓷磚膠的不均勻變形，進(jìn)而降低瓷磚膠與瓷磚的接觸面積S1。VC-SV模式下接觸面積S1顯著增大，其主要是因?yàn)榧羟姓駝?dòng)過程中瓷磚膠僅發(fā)生均勻的塑性變形且卸載后豎向彈性變形為零。

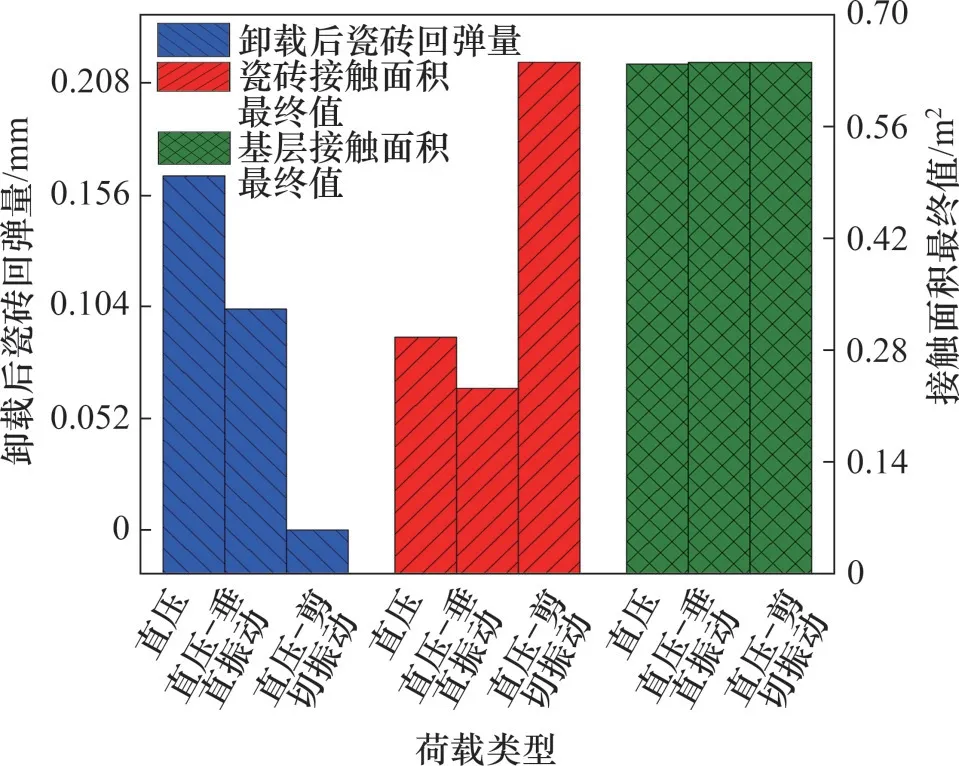
圖13 不同類型荷載作用時(shí)瓷磚的鋪貼質(zhì)量Fig.13 Installation quality of ceramic tiles under the actions of various loads

圖14所示為不同加載模式對(duì)瓷磚-瓷磚膠界面缺陷分布的影響。從圖14可見：與單一直壓荷載作用下的脫空條紋不同，耦合垂直振動(dòng)荷載后，瓷磚膠的不均勻變形不僅增大了脫空面積，而且脫空區(qū)域主要集中分布在瓷磚四周。這些大尺寸鋪貼缺陷的存在將顯著加速硬化后瓷磚空鼓的進(jìn)一步發(fā)展。而耦合剪切振動(dòng)后，瓷磚基本滿漿，僅出現(xiàn)少量均勻分布的極細(xì)脫空條紋，鋪貼質(zhì)量最優(yōu)。

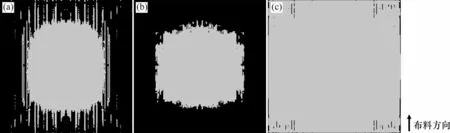
圖14 不同類型荷載作用時(shí)瓷磚-瓷磚膠界面缺陷的分布云圖Fig.14 Contour plots of the distribution of tile-adhesive interfacial defect under the actions of various loads

4 結(jié)論

1) 垂直布料的瓷磚膠塑性變形較大，瓷磚膠條形態(tài)坍塌為半圓柱狀，導(dǎo)致膠條間距縮小；水平布料的瓷磚膠塑性變形較小，瓷磚膠條的形態(tài)保持不變，呈等間距分布。

2) 隨著布料管數(shù)的增加，瓷磚膠條間隙縮短，引起瓷磚-瓷磚膠界面缺陷(脫空條紋)明顯變窄且分布更加均勻，瓷磚回彈量、瓷磚-瓷磚膠接觸面積以及瓷磚膠-混凝土基層接觸面積基本不變。

3) 在加載過程中，瓷磚膠發(fā)生彈性變形和塑性變形，接觸面積逐漸增大；直壓荷載和垂直振動(dòng)荷載卸載后，瓷磚發(fā)生回彈，瓷磚-瓷磚膠接觸面積隨之減小，瓷磚膠-混凝土基層接觸面積基本保持不變；剪切振動(dòng)荷載卸載后，瓷磚基本不回彈，接觸面積均保持不變，界面幾乎無(wú)缺陷。

4) 與直壓荷載相比，耦合垂直振動(dòng)荷載會(huì)使瓷磚膠的不均勻塑性變形增加，盡管瓷磚回彈量降低37.58%，但瓷磚-瓷磚膠接觸面積減小21.62%；耦合剪切振動(dòng)荷載后，瓷磚膠產(chǎn)生均勻塑性變形，瓷磚回彈量降低100.00%，導(dǎo)致瓷磚-瓷磚膠接觸面積增大116.22%。

5) 相比于拉格朗日法和歐拉法，采用CEL方法模擬瓷磚智能化鋪貼不僅可以計(jì)算鋪貼過程中瓷磚膠的大變形行為，而且能夠精確地捕捉瓷磚膠與瓷磚以及瓷磚膠與混凝土的接觸界面的變化。采用該法所獲得的計(jì)算結(jié)果與試驗(yàn)結(jié)果吻合較好，表明CEL方法在研究瓷磚鋪貼質(zhì)量方面具有較高的可靠性與較強(qiáng)的適用性。

致謝：感謝北京交通大學(xué)高性能計(jì)算校級(jí)平臺(tái)的支持和幫助。