基于深度強化學習的多無人車系統編隊控制1)

曾毓凌 郝宇清 于 穎 王青云

(北京航空航天大學航空科學與工程學院,北京 100191)

引言

21 世紀以來,隨著半導體技術、車輛技術、控制科學、人工智能和通信技術的不斷發展,無人機和無人車等新穎的運載設備逐漸從最初的創意設計變成了我們日常生活中的一部分.隨著工業發展中不斷升級的制造需求和對更先進的生產力需求,無人車和無人機等工具也從一個傳統的運載體向智能體的方向發展,其智能化程度正在飛快發展.然而,由于現代工程的復雜性和多樣性,許多任務很難通過單個智能體完成,如大型設備的搬運和組裝、大規模搜索與識別、復雜礦洞的數字建模,以及多樣性的軍事作戰任務等.在許多這樣的場景中,多智能體的協作往往能比進行單一智能體的功能擴充帶來更好的效果,例如節省復雜系統的研發成本,減少對硬件和軟件復雜性的要求[1].一個典型的例子就是在空戰中不同種類飛機的配合,其協同作戰效率和能力遠大于將所有功能集成于單一飛機[2].

關于多智能體協同控制問題,目前主要的研究方向有一致性控制[3-4]、編隊控制[5]和編隊-合圍控制[6]等.多智能體協同控制的控制器設計方法目前主要有領導-跟隨法[7-8]、虛擬結構法[9]、基于行為法[10]及基于一致性理論的方法[11-12]等.但現有的控制器設計方法大多是基于精確的線性模型,不能很好地刻畫地面輪式車輛等運載體的動力學行為.無人車的動力學行為具有較強的非線性,且存在非完整約束和欠驅動問題,傳統的基于線性系統理論設計的控制器有時候在實際無人車控制中效果欠佳.況且,當模型具有不確定性時基于精確模型的控制方法魯棒性較差.而機器學習的方法具有強大的擬合能力,對模型的要求度低,已廣泛應用在各種力學問題當中[13].相較于基于精確模型設計控制器的方法,強化學習的基本思路不再是人為地利用多智能體的精確模型設計各種形式的控制器,而是利用機器學習的方法建立高維狀態空間到動作空間的映射,相當于一個黑箱控制器模型,是一種較為新穎的控制器設計方式[14].結合了深度神經網絡的深度強化學習在特征表示方面具有非常強大的能力,該能力在構建狀態-動作映射時發揮了重要作用,在非線性動力學與控制問題以及欠驅動控制問題中具有較好的應用價值[15].況且,模型的訓練只需要智能體的輸入輸出數據,而不需要系統的精確模型,本質上是一種數據驅動的無模型控制方法,在模型參數未知、模型存在擾動和攝動時仍然可以學習到控制器[16].傳統的基于模型的控制方法與基于深度強化學習的控制方法的優缺點對比如表1 所示.

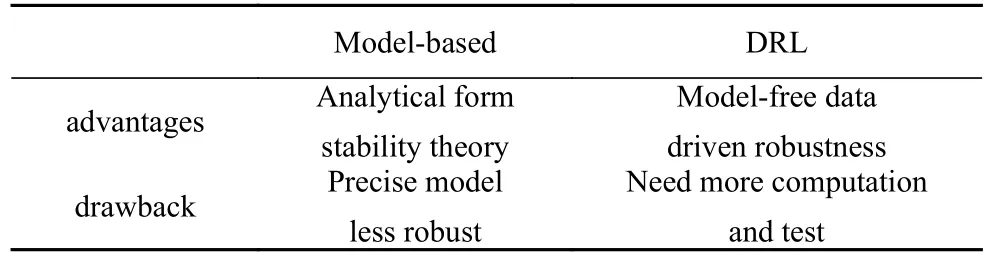
表1 兩種控制方法對比Table 1 Comparison of two control methods

Bae 等[17]結合CNN 卷積神經網絡和強化學習算法解決了多機器人的路徑規劃問題.Zhu 等[18]利用MADDPG 算法解決多機器人運動避障問題,并加入了優先經驗回放機制來更好地利用強化學習隨機動作儲存的經驗數據,但其使用的是質點運動學模型,并不能很好地刻畫真實的多智能體運動.Hung等[19]利用Q-learning 的強化學習算法,結合無人機運動學模型,解決了領導-跟隨問題.李波等[20]利用MADDPG 算法解決無人機群在威脅區域中的“避險”飛行問題.張海峰等[21]針對非線性多智能體控制問題,利用HJB 方程來設計控制律,并利用強化學習的方法來求解HJB 方程進而得到最優控制器.趙啟等[22]利用D3QN 深度強化學習算法和無人機運動學模型來研究長機-僚機編隊的橫向距離保持問題,后續又采用DDQN 深度強化學習算法研究長機-僚機編隊中的橫向距離保持和縱向速度跟蹤問題[23].馬曉帆[24]主要研究了商用車隊的編隊道路運行問題,構建了六自由度商用車動力學模型,利用TD3 算法來實現車隊的縱向編隊運行.相曉嘉等[25]提出了ID3QN 算法來研究固定翼無人機的定高長機-僚機編隊問題,ID3QN 算法是在D3QN 的基礎上增加“模仿”行為,旨在幫助僚機更快速地取得跟蹤長機效果較好的經驗數據.以上文獻主要基于運動學模型進行控制器設計,但實際的動力學系統往往是二階系統,由于慣性的存在,速度控制必然存在一定時延,力控制是最直接而準確的控制方式,在實際工程問題中具有更好的應用價值.

本文旨在利用深度強化學習技術設計多無人車系統的編隊控制器,使多無人車系統形成指定的期望隊形,并對控制器進行策略優化.本文的創新點包括以下三個方面.第一,基于DDQN 深度強化學習算法,結合一致性理論和伴隨位形的思想設計多無人車系統的編隊控制器,該控制器在無精確模型只有運動數據時也可以實現編隊控制任務,降低了對模型的依賴性,相比傳統的基于模型設計的控制器,本文給出的控制器魯棒性更強;第二,相較于目前大多數文獻基于運動學模型設計控制器,本文直接基于動力學模型設計力控制器,更具有實際意義;第三,本文創新性地提出了編隊起始階段的等候與啟動條件,進行了策略優化,仿真顯示優化后的策略有效節省了編隊所需的能量.

1 無人車動力學模型

常見的車輛動力學模型有阿克曼轉向模型[24]、麥克納姆輪轉向模型[26]和后輪差動轉向[27]等.后輪差動轉向的車輛硬件與結構更加簡單,常用于小型輪式機器人等.本文擬采用后輪差動轉向的剛體無人車動力學模型.

考慮后輪差動轉向的無人車模型,其左右兩側后輪由兩個電機獨立驅動,兩側的前輪僅用于支撐車輛和配合運動,不產生控制作用[28].無人車相對慣性坐標系定義的位形坐標為 η=(x,y,θ)T,代表了無人車的質心位置以及車頭朝向,無人車的幾何模型如圖1 所示,各參數如表2 所示.

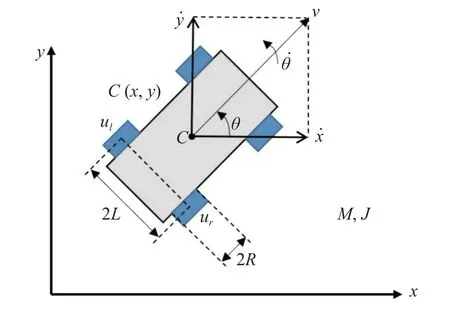
圖1 無人車幾何模型Fig.1 Unmanned vehicle geometric model

表2 無人車幾何參數Table 2 Unmanned vehicle geometric parameter

無人車的動力學方程為[29]

需要注意的是,該無人車動力學模型僅僅用于運動的仿真和運動數據的獲取,在控制器的設計與訓練中并不需要該動力學模型.

2 基于DDQN 的多無人車編隊控制

2.1 問題描述

考慮含有N+1 個無人車的多無人車系統,其中包含1 個領導者無人車和N個跟隨者無人車,其狀態由位形坐標與速度變量表示.無人車的位形坐標記作xi=(xi,yi,θi),i=1,2,···,N;其速度變量記作vi=(vi,ωi),i=1,2,···,N.其中第0 號無人車為領導者,第1 至N號無人車為跟隨者.

編隊控制問題的控制目標是使得多無人車系統形成期望的隊形,如下式所示

2.2 問題分析

為了實現多無人車系統的編隊控制,可以先從單領導者單跟隨者問題出發,再利用樹狀通訊擴展到多無人車系統的編隊控制問題.首先考慮單個跟隨者和領導者的編隊控制,領導者狀態表示為xl=(xl,yl,θl) 和vl=(vl,ωl),跟隨者的狀態表示為xf=(xf,yf,θf)和vf=(vf,ωf) .任務目標為設計合適的控制器,使得跟隨者的狀態與跟隨者的狀態之差等于期望的相對位形d,即

觀察上式,可以構造領導者的伴隨位形 (xl-d),稱之為伴隨領導者.若跟隨者實現對伴隨領導者的一致性跟蹤,則等價于實現了對領導者的編隊控制.因此,可利用構造伴隨領導者的方法將編隊控制問題轉化為一致性問題.伴隨領導者的幾何示意圖如圖2 所示.

圖2 伴隨領導者Fig.2 Accompanying leader

2.3 DDQN 深度強化學習算法

強化學習技術作為機器學習的一個分支,憑借其在解決復雜的序列決策問題中的優異表現,在控制工程領域和多智能體協同領域得到了廣泛的應用[1].其基本思想是在無經驗的情況下通過智能體與環境的交互,獲取反饋并積累經驗,然后優化智能體的決策模型,其基本思想如圖3 所示.

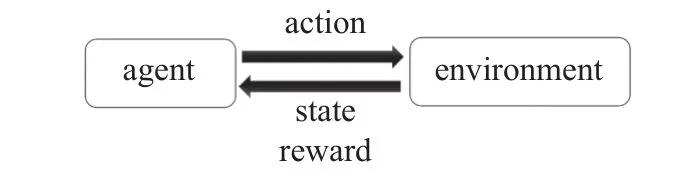
圖3 強化學習基本思想Fig.3 Reinforcement learning basic idea

DDQN 算法是一種經典的深度強化學習算法,全稱為double deepQnetwork learning,旨在利用深度學習的思想構建深度神經網絡來建立從智能體狀態st到價值函數Q(st,at) 的映射,其中st代表當前時刻的狀態,at代表智能體做出的動作,rt代表智能體在本次交互中獲得的獎勵[30].該算法的特點是構建了價值網絡與目標網絡兩個神經網絡,在訓練時可以有效避免因自舉現象產生的價值函數高估問題,具有較好的穩定性,且其原理和架構的復雜程度不高,對硬件的要求低,便于無人車系統部署.

強化學習的最終目標是學習到最優策略π*(a|s),使得期望折扣獎勵R最大,期望折扣獎勵定義為

其中,γ 為折扣因子,代表未來的獎勵折算到當前時刻的比例,rt為即時獎勵,T為終止時刻.獎勵函數r(s,a)通常根據具體任務來進行設計,便于針對性地進行優化,例如在多無人車一致性控制任務中加入位形誤差、速度誤差等變量.

準確的價值函數Q*(s,a) 代表的是神經網絡在狀態s下執行動作a所能獲得的期望折扣獎勵的期望值,其表達式為[13]

在學習到了準確的價值函數后,便可以在不同狀態下評估最優動作并進行控制.

2.4 控制器狀態與動作空間設計

為了實現利用DDQN 算法建立控制器實現控制目標的任務,需要設計合適的狀態空間和動作空間,在經過多輪測試后,選取局部坐標相比于慣性系下的全局坐標能使網絡學習到更準確的特征,控制效果會有明顯的進步,由于是設計跟隨者的控制器,故設計狀態空間時需要將領導者與跟隨者的全局坐標轉化為在跟隨者坐標系下建立的相對坐標,幾何示意圖如圖4 所示.

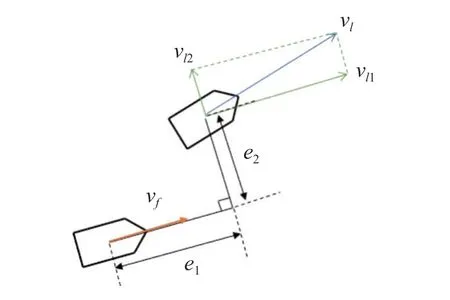
圖4 狀態空間Fig.4 State space

狀態空間定義為

其中,e1和e2為跟隨者坐標系下的縱向距離誤差和橫向距離誤差,vf為跟隨者的運動速度,vl1和vl2為領導者的運動速度在跟隨者坐標系下的縱向和橫向分量,ωf和ωl為跟隨者和領導者的角速度.各個局部坐標變量與慣性坐標系下的變量轉換關系為

考慮到DDQN 算法輸出神經元數量有限,需要將動作空間進行離散化,才能使輸出層的各個神經元輸出價值函數Q(s,a)[31].本文基于無人車系統動力學模型來設計控制器,控制輸入為左右側后輪的轉矩,需要對驅動力矩進行控制來改變運動狀態.其轉矩的和值控制無人車縱向的加減速,其轉矩的差值控制無人車沿豎直方向的角加速度.考慮到縱向加減速可分為加速、減速和保持速度3 個動作,轉動增大角速度、減小角速度和保持角速度3 個動作,兩個維度耦合后可以得到9 種動作,因此取動作空間為9 種典型動作構成的集合.

2.5 控制器訓練環境

為了使網絡學習到符合實際物理意義的價值函數Q(s,a),需要針對控制目標設計對應的獎勵函數,顯然一致性控制問題下,位形誤差與速度誤差越小,系統的狀態越佳,因此設計獎勵函數為

其中,相對距離與相對速度的計算方法如下

該獎勵函數的具體含義是: 相對距離越小,狀態越接近一致,具有更高的價值,所以獎勵與相對距離呈負相關,不同區間的不同梯度有助于模型在誤差較小時提高敏感性,避免在誤差較小的區間內因為獎勵函數的值變化較小而學習效果不佳.在本任務中,取ed=0.01 m 為收斂閾值,認為距離誤差小于該閾值時實現了一致性跟蹤,故距離獎勵的最大值定義在ed＜0.01 m 的情況.將相對速度引入較小的負獎勵可以使模型的過渡階段盡量平滑,避免出現過大的速度差值.

基于以上的狀態與動作空間、獎勵函數以及無人車剛體動力學模型,便可以構建基于DDQN 算法的一致性控制器訓練環境和運動仿真環境,如圖5 所示.

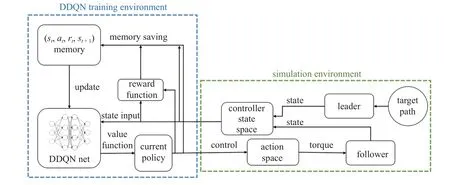
圖5 控制訓練環境Fig.5 Controller training environment

在每一個控制周期內,無人車將狀態變量輸入神經網絡并得到價值函數輸出,然后利用動作選擇策略來決定跟隨者的控制量,訓練時常采用帶有一定隨機性的動作選擇策略來使得網絡探索更多的動作.動作選擇完成后,環境將更新領導者與跟隨者的下一狀態,并計算該次控制得到的獎勵函數,然后將經驗數據即環境交互得到的四元組(st,at,rt,st+1)存入經驗記憶庫,再從經驗庫中采樣并更新網絡.

為了在網絡訓練時模擬到更全面更復雜的環境來指導神經網絡的更新,避免網絡陷入局部最優,在設計訓練場景時需要充分增加隨機性,避免因為軌跡和場景的單一導致網絡過擬合,泛化性差.因此考慮如圖6 所示的4 種典型運動,分別為勻速直線運動、加減速、左轉和右轉.

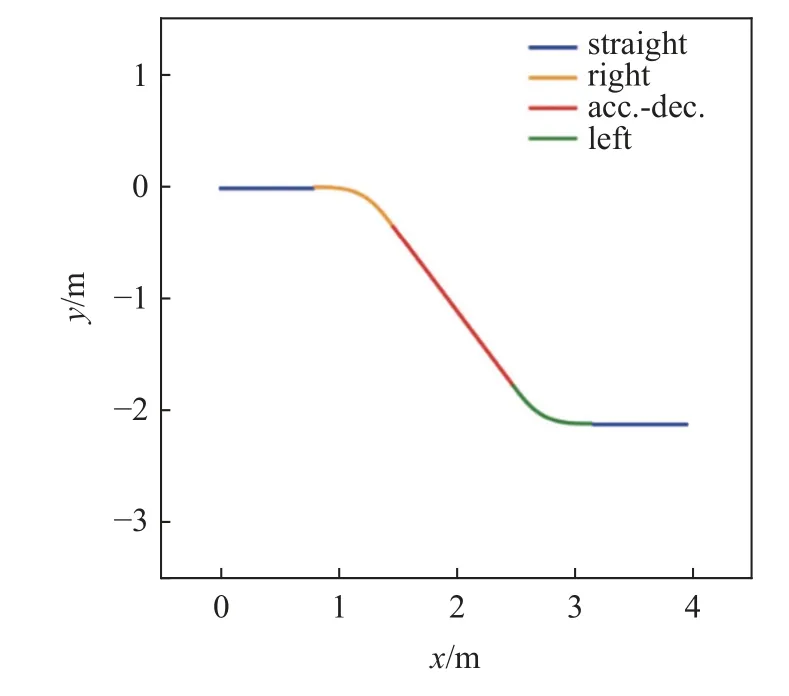
圖6 4 種典型運動軌跡Fig.6 Four typical trajectories

在每一輪訓練開始前,環境會生成 40 s 的領導者運動軌跡,其中每 4 s 為一段.每一輪訓練共由10 段軌跡拼接而成,每一段軌跡都為上述4 種典型軌跡之一,且為均勻抽樣,以實現訓練過程的領導者軌跡多樣性.

在訓練中,領導者無人車的起始位形和速度為(xl0,yl0,θl0,vl0,ωl0)=(0,0,0,0.2,0).跟隨者的起始位置在以領導者起始位置為中心,以 6 m 為邊長的正方形內隨機生成,起始姿態角,按照均勻分布隨機選取.

神經網絡的結構及參數如圖7 和表3 所示.

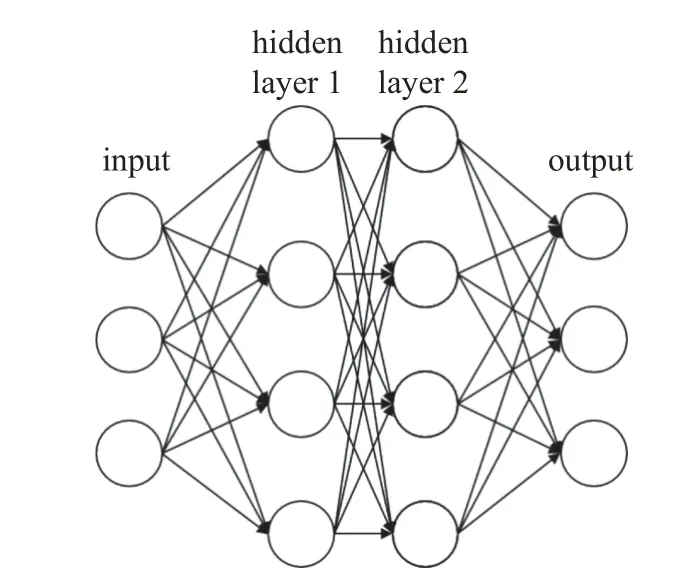
圖7 神經網絡結構Fig.7 Neural network framework

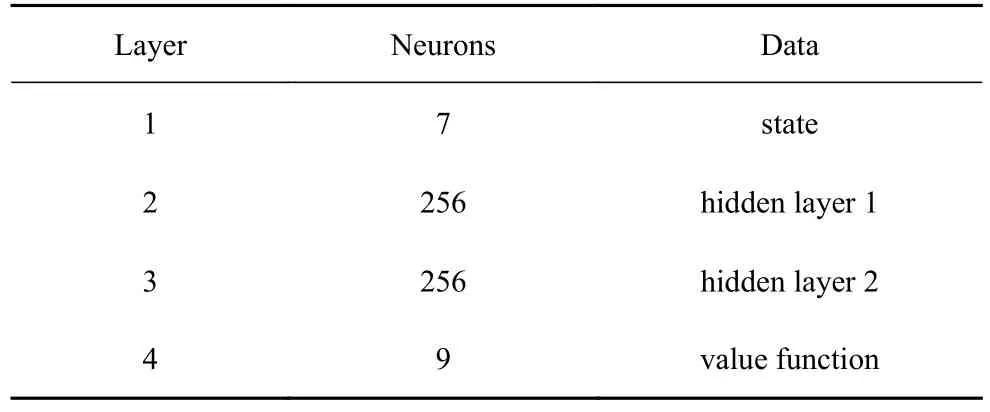
表3 神經網絡參數Table 3 Neural network parameters

2.6 控制器訓練結果

基于以上的訓練環境,設置網絡訓練的總輪次為10 000 輪,初始學習率為0.000 1,記憶庫總容量D為 218,每次更新網絡的采樣數量為256,折扣因子γ為0.95,訓練結果如圖8 所示.

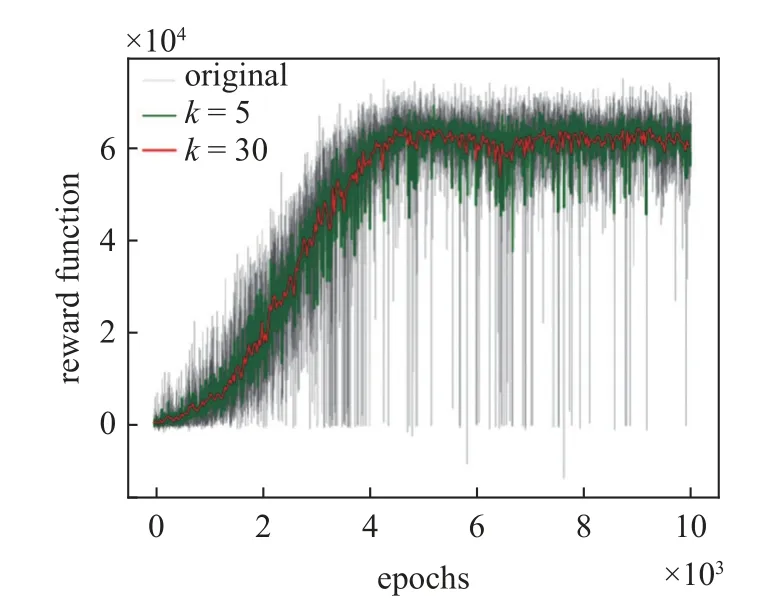
圖8 訓練結果Fig.8 Training result

可以看到,隨著網絡的訓練,每輪次所獲得的獎勵函數和值在不斷增大,網絡訓練后期獎勵函數和值趨于收斂.由于網絡訓練時模型決策因為有較小的探索率會存在動作的隨機選擇,并且每個輪次的領導者軌跡與起始位置不同,因此會造成獎勵函數和值的波動,可用滑動窗口平均值觀察網絡的收斂性,圖中取窗口大小k=5和k=30 兩組參數進行繪圖,可以觀察到網絡在訓練后期收斂于較高的獎勵值,模型趨于收斂.然后,將動作選擇策略的隨機性消除,按照價值最大策略進行控制,對模型進行驗證,控制器結構圖如圖9 所示.

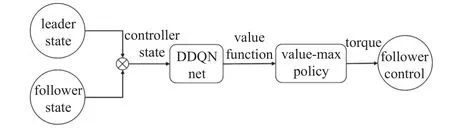
圖9 控制器結構Fig.9 Controller framework

進行100 輪驗證,結果如圖10 所示.

圖10 驗證結果Fig.10 Test result

同樣使用滑動窗口平均法觀察驗證過程的獎勵函數,可以觀察到模型的表現較為穩定,曲線有所波動的原因與領導者軌跡的隨機性和初始位置的隨機性有關.經驗證,該網絡可以在訓練場景下實現跟隨者狀態對領導者狀態的跟蹤.

3 仿真驗證

3.1 運動仿真結果

考慮由5 臺無人車組成的多無人車系統,通訊方式為樹狀拓撲,如圖11 所示.其中,0 號無人車為領導者,其他為跟隨者,其中1 號和3 號無人車都與領導者進行通訊,可以獲取領導者的運動狀態,但2 號和4 號無人車只能分別與1 號和3 號無人車進行通訊,獲取對應無人車的狀態,而不能得到領導者的運動狀態,以模擬分布式通訊的場景.領導者按照期望軌跡進行運動,跟隨者在控制器的控制下運動.

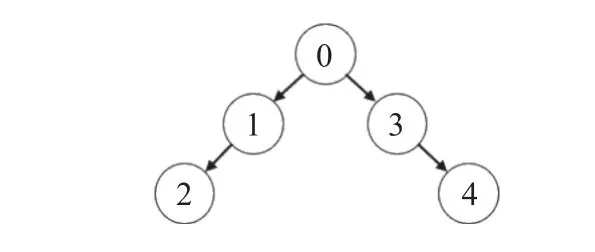
圖11 通訊拓撲Fig.11 Communication topology

各無人車的物理參數如表4 所示.

表4 無人車物理參數Table 4 Unmanned vehicle physical parameter

無人車的初始位形為

無人車的期望隊形為五邊形,具體的隊形參數為

引入期望隊形的信號后,便可將一致性控制器轉化為編隊控制器,控制器的結構圖如圖12 所示.

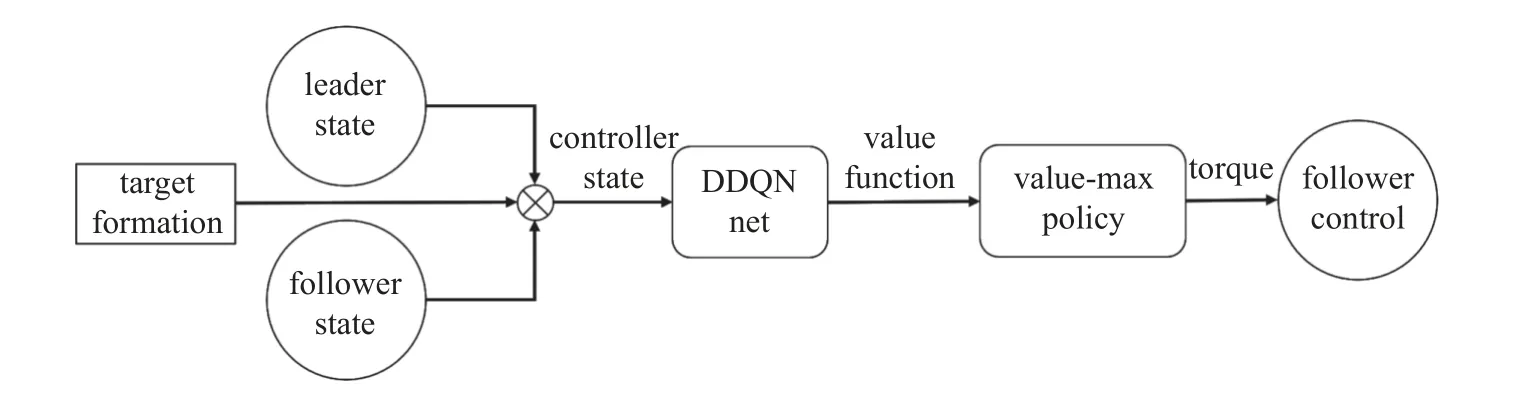
圖12 編隊控制器結構Fig.12 Formation controller framework

設置期望隊形為五邊形,領導者運動軌跡覆蓋加減速、左右轉等情況,所有跟隨者初始時刻靜止,進行運動仿真,結果如圖13 和圖14 所示.

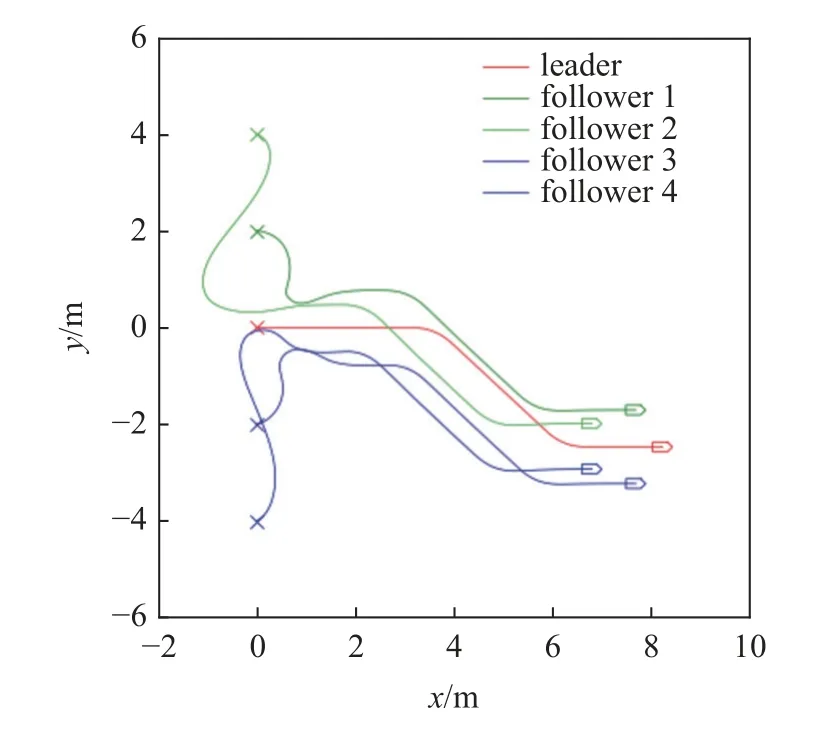
圖13 無人車軌跡Fig.13 Unmanned vehicle trajectory

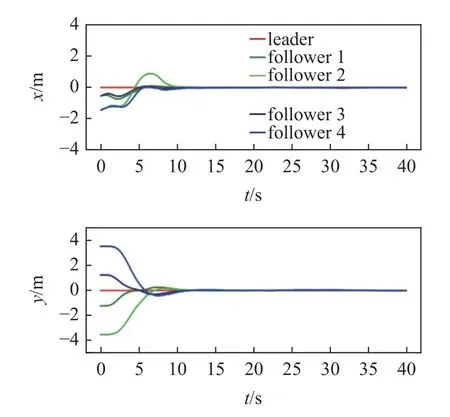
圖14 編隊誤差曲線Fig.14 Formation error

根據運動軌跡和誤差曲線可以觀察到,多無人車系統在該控制器的控制下成功實現了期望的編隊運動.

為了充分驗證控制器的有效性,需要針對不同的期望隊形開展運動仿真實驗,圖15 和圖16 為不同期望隊形的運動仿真結果,其中圖15(a)和圖16(a)為五邊形隊形,圖15(b)和圖16(b)為平行隊形,圖15(c)和圖16(c)為合圍四邊形隊形.領導者運動軌跡也包含了左右轉、加減速等典型運動情況.通過運動軌跡和誤差曲線可以看到,不同期望隊形下,控制器均能驅動多無人車系統快速實現編隊并保持隊形穩定運動.

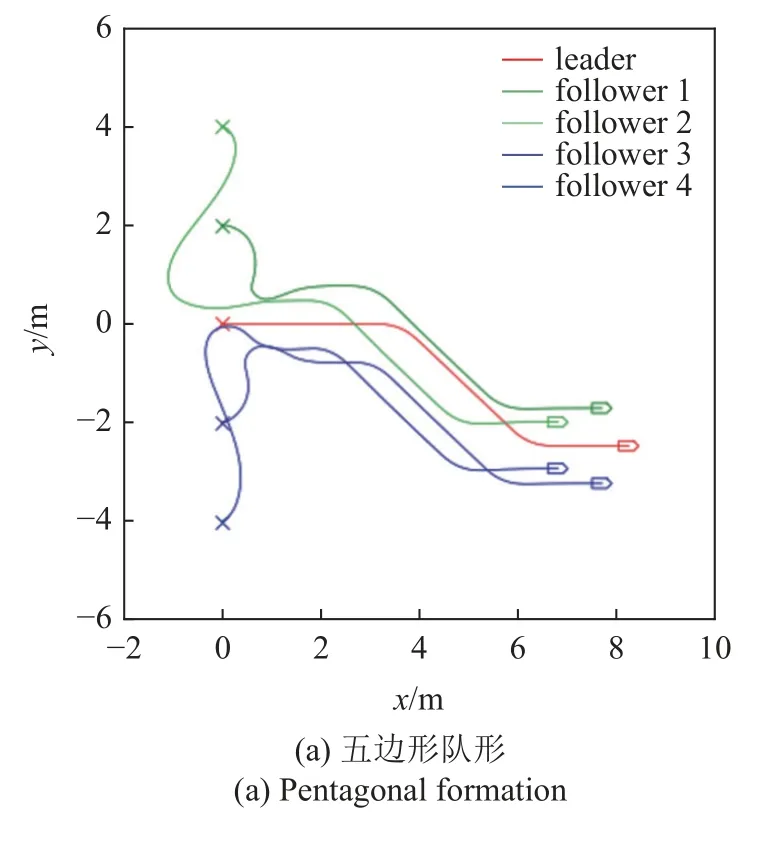
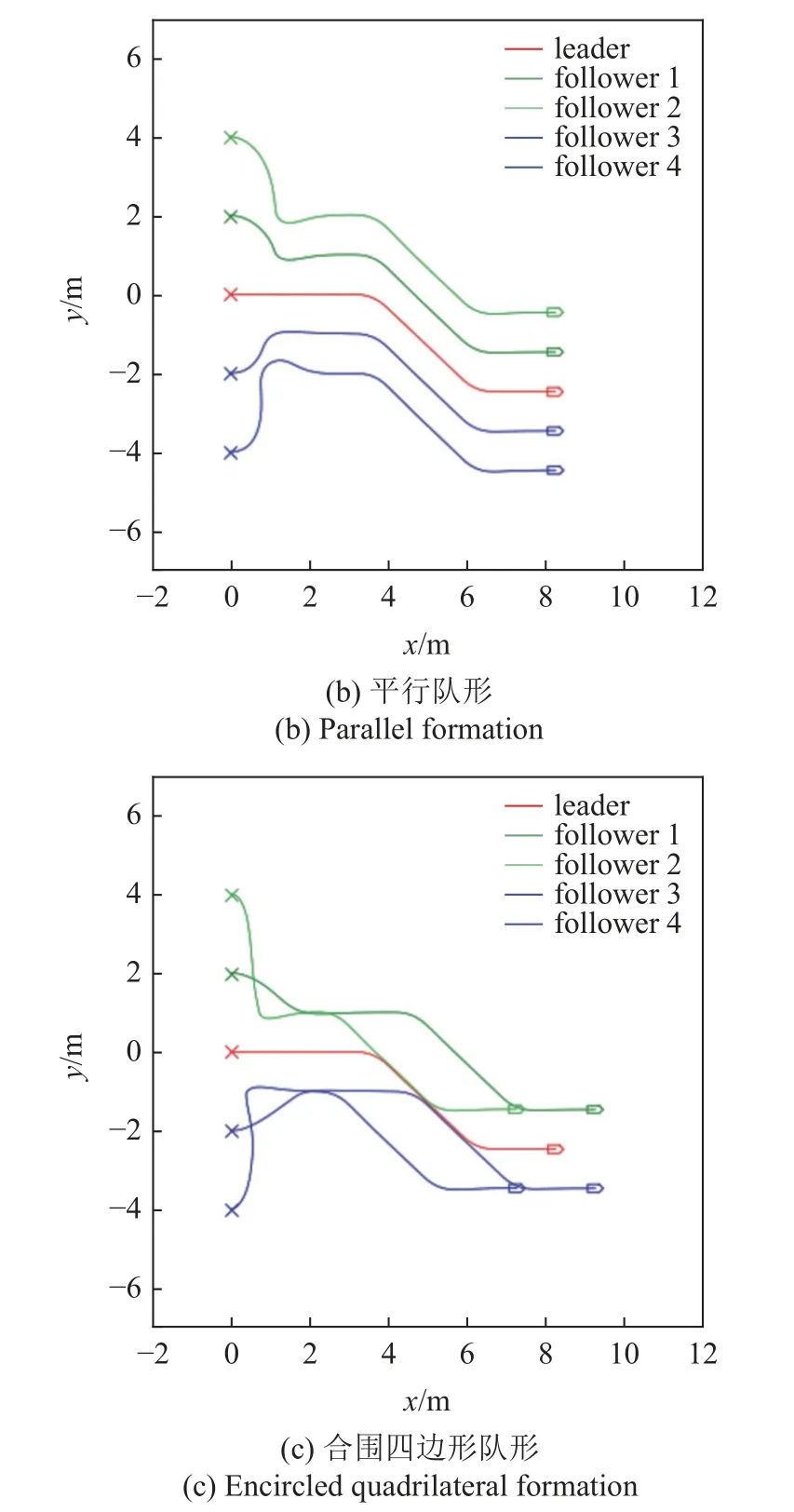
圖15 多隊形測試軌跡Fig.15 Multiple formation testing trajectory

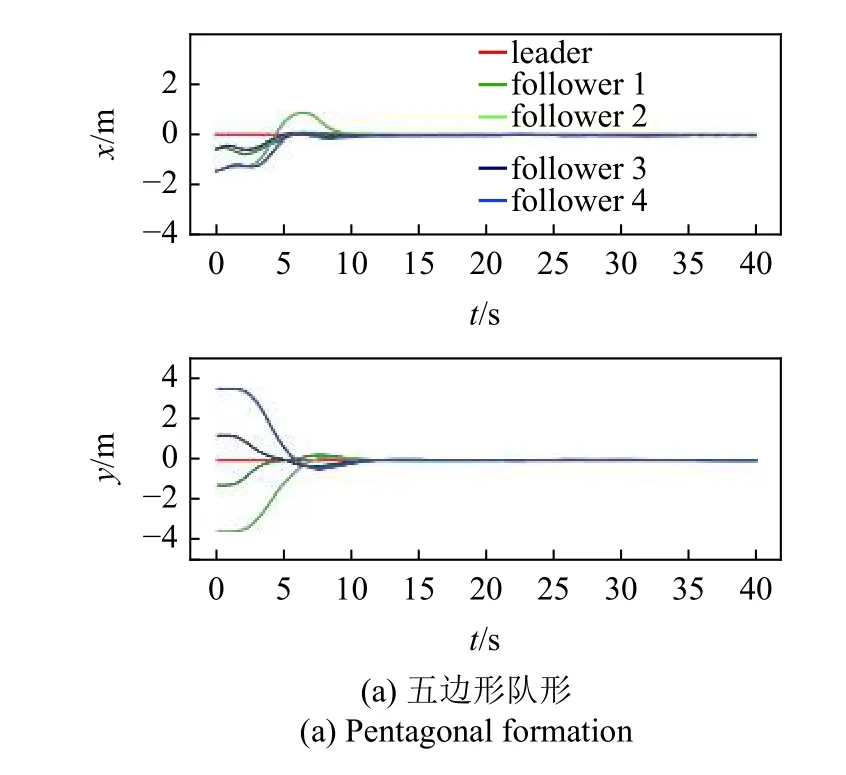
圖16 多隊形測試誤差曲線Fig.16 Error plot of multiple formation testing

在現實場景中,往往由于地形等原因,多無人車編隊需要在運動過程中進行隊形切換,因此需要驗證控制器在運動過程中變換隊形的能力.圖17 和圖18 為隊形切換的運動仿真結果,多無人車系統在運行過程中由于遇到障礙需要收緊隊形,通過后恢復原隊形.運動軌跡和誤差曲線顯示多無人車系統能夠在控制器的驅動下,在運動過程中期望隊形發生變化時快速轉換為新目標隊形,驗證了在運動過程中的隊形切換能力.

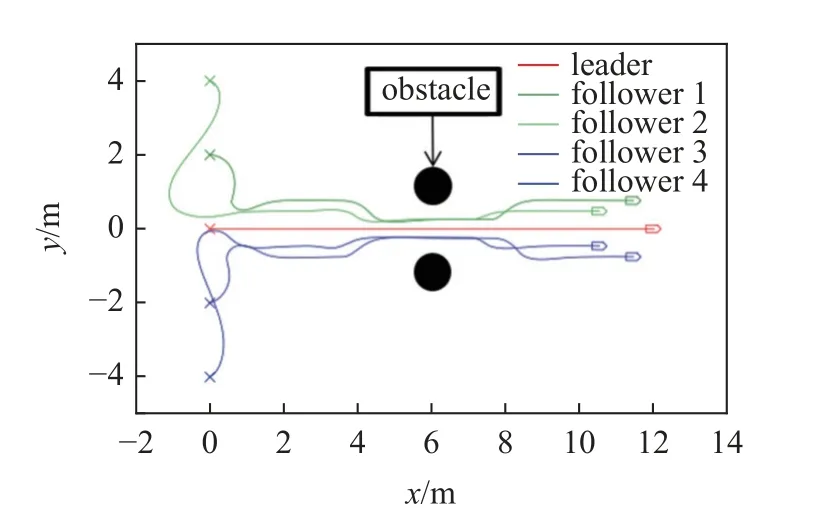
圖17 隊形切換測試軌跡Fig.17 Formation switching test trajectory

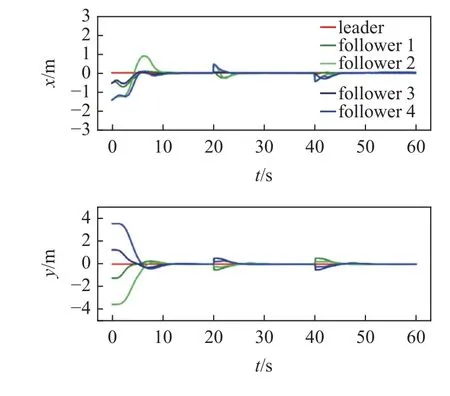
圖18 隊形切換測試誤差曲線Fig.18 Formation switching test error plot

3.2 起始階段策略優化

上文中的運動仿真證明了編隊控制器的有效性,但通過對多無人車系統運動軌跡的觀察可以發現,在編隊控制的多隊形實驗中,當無人車起始位形為平行排布時,五邊形編隊任務中存在一定的反向運動現象,即運動過程中跟隨者與領導者的速度方向夾角出現鈍角,即vf·vl＜0,圖19 為第4 s 時刻的無人車狀態.

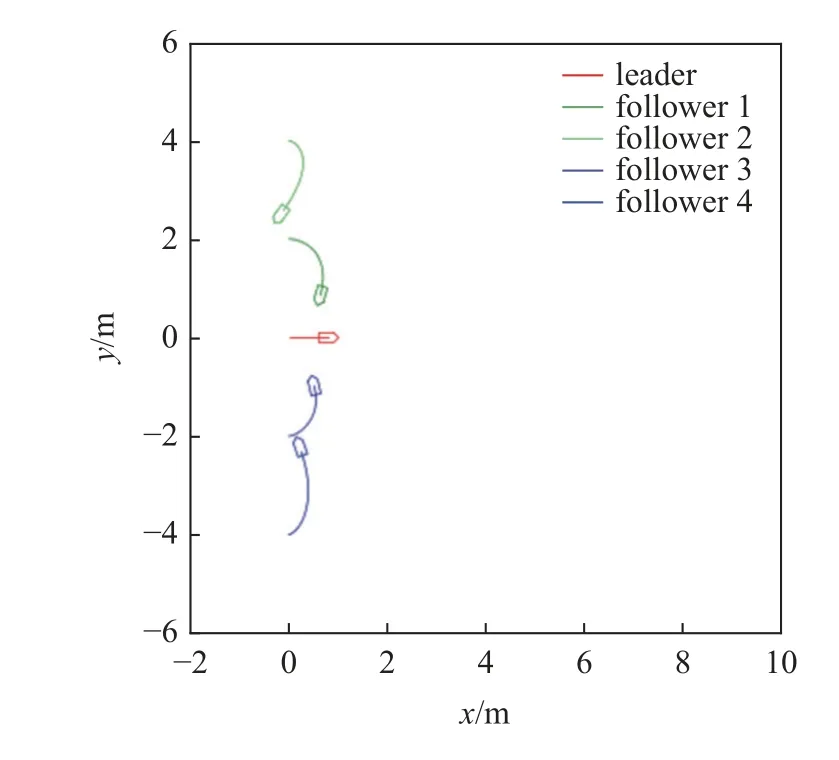
圖19 反向運動時刻Fig.19 Reverse movement moment

造成該現象的原因是在起始位形下根據領導者計算各個跟隨者的伴隨領導者時,跟隨者對伴隨者的縱向跟蹤誤差為負,也就是兩者之間的距離誤差在跟隨者的速度方向投影為負,導致跟隨者需要向領導者速度方向的反方向運動才能對伴隨領導者實現跟蹤,故存在“反向運動”現象,由于需要進行更多的轉向和加減速動作,該現象會增大控制過程中消耗的能量.

考慮單領導者-單跟隨者的編隊控制起始階段狀態.考慮 θf0=θl0且e1＜0,vl0≥0,vf0=0 的初始情況,如圖20 所示.

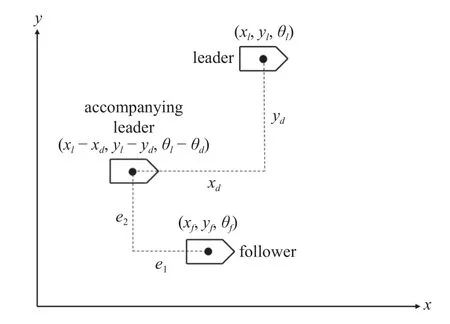
圖20 反向運動典型狀態Fig.20 Reverse movement typical condition

顯然,該初始情況與上述五邊形編隊的所有跟隨者的情況相同,是典型的易引起反向運動的起始條件.然而顯而易見的是,該情況下若跟隨者保持靜止等候,在短時間內也會由于領導者的自身運動而使得編隊誤差減小,而不消耗任何能量,這是因為e1＜0,vl1-vf＞0,兩者縱向的相對速度與位置誤差異號,故縱向位置誤差的大小將在一定時間內自行減小.由于考慮 θf0=θl0的初始情況,在起始時刻臨近的短時間內橫向誤差e2基本不變,為簡化模型暫不考慮橫向的誤差狀態.

為了消除反向運動情況,現基于領導者與跟隨者的縱向狀態量定義單個無人車的等候條件與啟動條件,等候條件為

其物理含義為,縱向距離誤差與速度誤差符號相反,具有自發消除誤差的趨勢,因此跟隨者保持靜止不動仍然能使得編隊誤差減小.

定義啟動條件為

其物理含義為,縱向距離誤差與速度誤差符號相同,位置誤差的絕對值將趨于增大,因此必須引入編隊控制器的作用來驅動各個無人車達成期望隊形.

各個無人車從初始時刻開始,在每個時間差分內都要進行等候條件與啟動調節的判斷,若滿足等候條件則不進行控制,保持初始狀態;若滿足啟動條件,則由DDQN 編隊控制器持續進行控制.需要注意的是,由于以上分析都是基于 θf0=θl0的運動初始階段,該動作策略僅用于運動初始階段的能量優化,每個無人車一旦在某時刻達到啟動條件,在后續時刻就不再進行條件判斷,而是由編隊控制器驅動無人車以實現控制目標.

3.3 對比分析

為了驗證該策略的作用,采用五邊形編隊進行運動仿真以對比分析.運動仿真結果如圖21 和圖22所示.

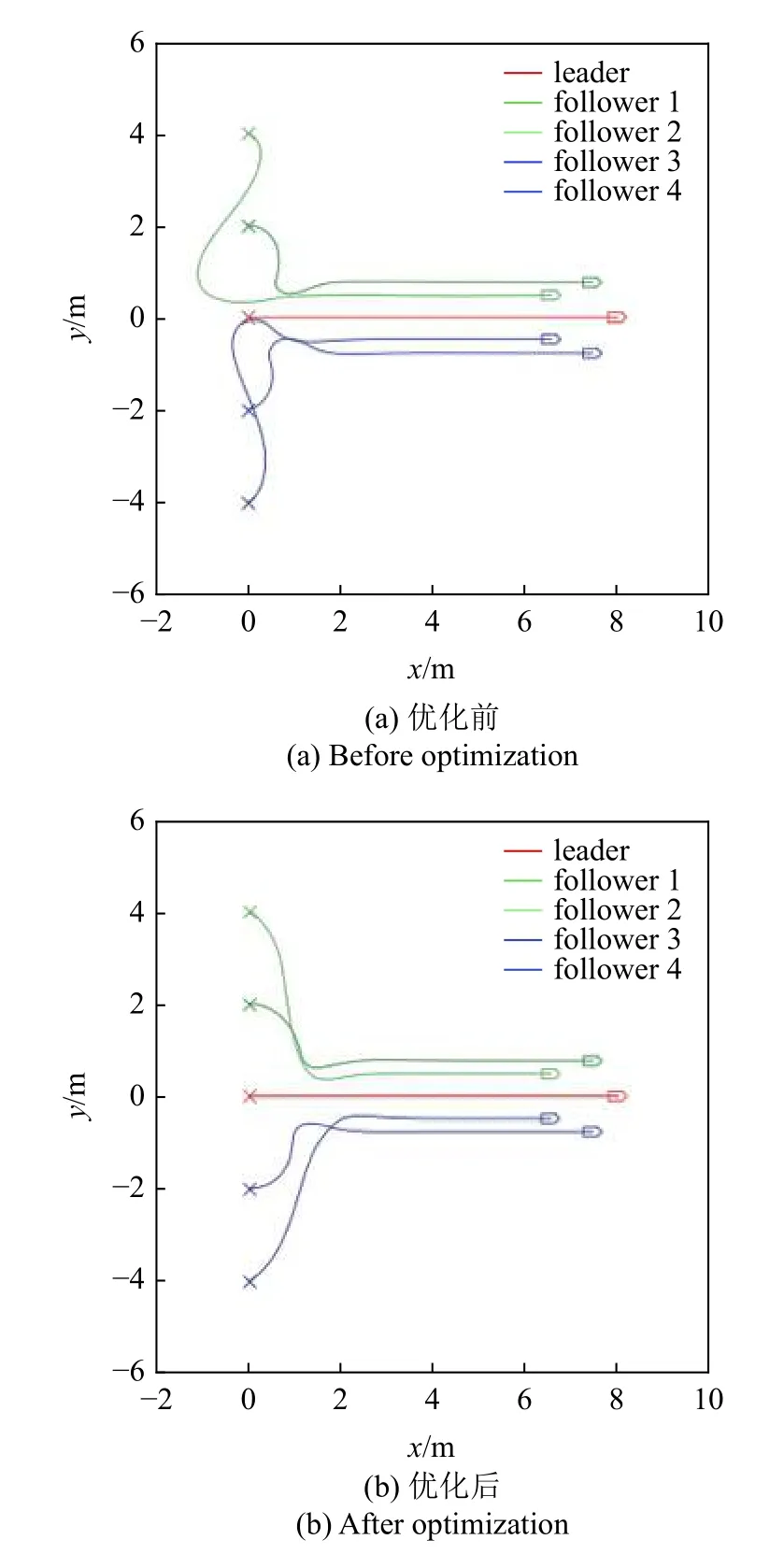
圖21 運動軌跡對比圖Fig.21 Trajectory comparison

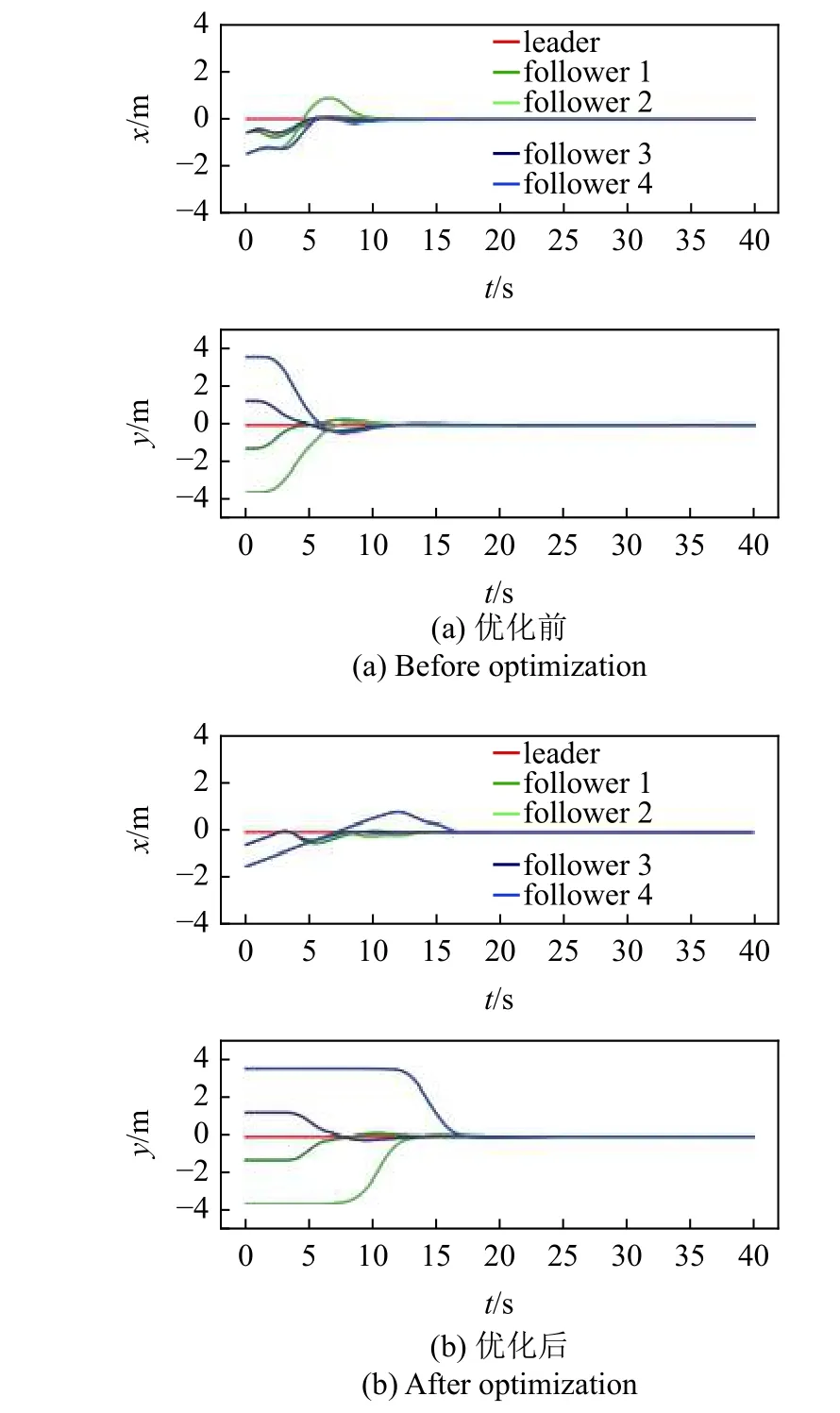
圖22 誤差曲線對比圖Fig.22 Error-curve comparison

其中,圖21(a)和圖22(a)分別為優化前的運動軌跡與誤差曲線,圖21(b)和圖22(b)為優化后結果.經計算,加入該策略后,運動過程中所消耗的能量減少了19.93%,有效驗證了該策略節約能量的作用,并且通過對運動軌跡的觀察可以發現該策略消除了反向運動現象.但值得注意的是,由誤差曲線的對比可知,能量優化伴隨著收斂時間增大的代價,這是由于等候的過程實際上消耗了一定的時間.雖然該策略可以在節省一部分能量的情況下完成編隊任務,但因為其設計原理而必然伴隨著收斂時間延長.

4 總結

本文基于DDQN 深度強化學習算法,結合一致性理論與伴隨領導者設計了多無人車系統的編隊控制器.首先,進行了編隊問題簡化,將編隊控制問題轉化為對伴隨領導者的一致性跟蹤問題,然后簡化為單領導者-單跟隨者問題,并對該問題設計了基于跟隨者局部坐標系的7 維狀態空間、9 維動作空間和基于距離誤差和速度誤差的獎勵函數.然后搭建了DDQN 網絡的訓練環境,設計神經網絡架構參數后,引入初始位置和領導者訓練軌跡的隨機性進行網絡訓練.訓練完成后利用運動仿真驗證了控制器的有效性,并針對運動中所存在的反向運動現象,從編隊控制器中的動作選擇策略層面提出了編隊控制器起始階段策略優化方法.在運動初始時,定義了等候條件與啟動條件,對部分無人車進行延遲啟動,仿真驗證了該策略具有一定的能量節約作用,但可能會增加收斂時間.