基于學(xué)生問題意識培養(yǎng)的初中數(shù)學(xué)教學(xué)探索
陸青


當下,部分教師會關(guān)注學(xué)生分析和解決問題的能力的培養(yǎng),卻忽視了培養(yǎng)學(xué)生發(fā)現(xiàn)問題和提出問題的能力。一味強化學(xué)生分析和解決數(shù)學(xué)問題的能力,很難讓學(xué)生達到“用數(shù)學(xué)的眼光觀察現(xiàn)實世界,用數(shù)學(xué)的思維思考現(xiàn)實世界,用數(shù)學(xué)的語言表達現(xiàn)實世界”,所以,初中數(shù)學(xué)的課堂教學(xué)應(yīng)該關(guān)注學(xué)生發(fā)現(xiàn)問題的意識及能力的培養(yǎng),而問題意識的培養(yǎng)是學(xué)生提出問題的前提。下面,筆者以“圖形的旋轉(zhuǎn)”復(fù)習(xí)課為例,談?wù)剬趩栴}意識培養(yǎng)的教學(xué)實踐的探索。
一、設(shè)計理念
平移、旋轉(zhuǎn)和翻折是幾何變換中的三種基本變換,九年級學(xué)生對此已充分了解。筆者從三個方面進行思考,以更大程度地培養(yǎng)學(xué)生的問題意識,增強學(xué)生的空間觀念和推理能力。一是問題意識的引導(dǎo)。學(xué)生在面對某一學(xué)習(xí)對象的時候,如果能夠自發(fā)地產(chǎn)生問題,也就意味著引導(dǎo)成功了。所以,教學(xué)要以容易激發(fā)學(xué)生興趣的情境或問題導(dǎo)入,讓學(xué)生產(chǎn)生迫切探究的欲望,為問題意識的產(chǎn)生做足準備。二是問題沖突的呈現(xiàn)。教師要在教學(xué)設(shè)計中創(chuàng)設(shè)足夠的探究空間,供學(xué)生自由思考和表達。三是問題解決的深化。問題設(shè)計要有“閉環(huán)”意識,通過開放性問題的設(shè)計,不斷分析、解決同一情境下的不同問題,或者從不同角度解決同一問題,尋找“變”中的“不變”。
二、教學(xué)片段
1. 情境引入(問題意識的引導(dǎo))
師:如圖1所示,靜止汽車的雨刮器在轉(zhuǎn)動時,你能找到雨刮器上的雨刷AB,繞著點O逆時針旋轉(zhuǎn)45°后的雨刷A′B′的位置嗎?
生:將雨刷看成一條線段AB,點O看成旋轉(zhuǎn)中心(圖2),作出線段AB關(guān)于點O逆時針旋轉(zhuǎn)45°后所得的線段。
師:很好,這就是一個基本的旋轉(zhuǎn)作圖。哪位同學(xué)為我們演示一下作圖的步驟?
學(xué)生在黑板上演示作圖(圖3),講解作圖步驟。
師:在這個變換中,你能得到哪些結(jié)論?
生:0A=0A′,OB=OB′,AB=A′B′,∠A0A′=∠BOB′。
師:旋轉(zhuǎn)的性質(zhì)有哪些?
生:對應(yīng)點到旋轉(zhuǎn)中心的距離相等;對應(yīng)點與旋轉(zhuǎn)中心所連線段的夾角相等且都等于旋轉(zhuǎn)角;旋轉(zhuǎn)前后的圖形全等。
師:你還能得到其他結(jié)論嗎?
生:∠AOB=A′OB′。
師:旋轉(zhuǎn)是一種全等變換,它只改變了圖形的位置,所以旋轉(zhuǎn)變換會產(chǎn)生很多相等的邊、相等的角、相等的線段。
【設(shè)計意圖】通過實際問題,思考畫旋轉(zhuǎn)圖形的方法、旋轉(zhuǎn)的本質(zhì)、旋轉(zhuǎn)后的結(jié)論,為后續(xù)的問題呈現(xiàn)和問題深化提供實踐基礎(chǔ)。
2. 自主探究(問題沖突的呈現(xiàn))
師:旋轉(zhuǎn)在生活中應(yīng)用廣泛,在數(shù)學(xué)中是解決平面幾何問題的重要工具之一,其看似簡單的變換可以產(chǎn)生很多復(fù)雜的問題,下面我們就從矩形的旋轉(zhuǎn)開始探究。
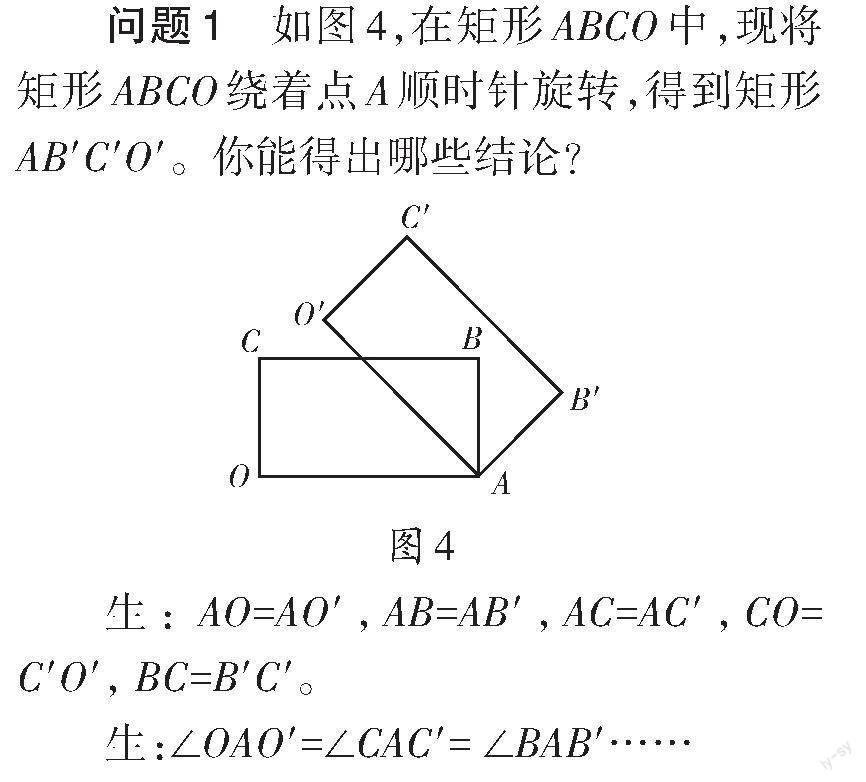
問題1 如圖4,在矩形ABCO中,現(xiàn)將矩形ABCO繞著點A順時針旋轉(zhuǎn),得到矩形AB′C′O′。你能得出哪些結(jié)論?
生: AO=AO′,AB=AB′,AC=AC′,CO=C′O′, BC=B′C′。
生:∠OAO′=∠CAC′= ∠BAB′……
師:除了全等、相等的線段和相等的角,還有其他結(jié)論嗎?大家可以進行討論交流。
生:我發(fā)現(xiàn),△CAC′、△OAO′、△BAB′相似。
生:通過相似還可以得到比值關(guān)系,CC′[∶]OO′[∶]BB′=AC[∶]AO[∶]AB。
師:你還有什么發(fā)現(xiàn)?
生:在圖形變換的過程中,有些關(guān)系、有些值是不變的。
【設(shè)計意圖】教師創(chuàng)設(shè)寬松和諧的課堂氛圍,逐步增強學(xué)生的自信心,給予學(xué)生獨立發(fā)現(xiàn)的時間,引導(dǎo)學(xué)生提出富有價值的問題。問題的呈現(xiàn)讓學(xué)生充分暴露自己的認知,并更加準確地描述和表達自己的認知。當不同的學(xué)生帶著不同的觀點參與課堂活動時,在該環(huán)節(jié),學(xué)生慢慢發(fā)現(xiàn)旋轉(zhuǎn)的不變性。在這個逐步遞進的過程中,教師應(yīng)當充分利用好合作學(xué)習(xí)這個環(huán)節(jié),讓學(xué)生在和諧的氛圍中表達自己的觀點。此時,問題意識的激活與深化起到了關(guān)鍵的作用。
3.變式訓(xùn)練(問題解決的深化)
問題2 如圖5,在矩形ABCO中,點B的坐標為(8,4),現(xiàn)將矩形ABCO繞著點A順時針旋轉(zhuǎn),得到矩形AB′C′O′。你能提出哪些問題?并嘗試解決問題。
生:可以求BB'與CC'的比值。
生:可以求OB′、OC′的范圍。
生:可以求旋轉(zhuǎn)45°后O′、B′、C′的坐標。
生:可以求圖形面積。
……
師:大家在設(shè)計問題、解決問題的過程中,有沒有什么發(fā)現(xiàn)或想法呢?
生:解決旋轉(zhuǎn)問題的根本是抓住變中的不變性。
【設(shè)計意圖】學(xué)生提問,學(xué)生解決,學(xué)生在智慧碰撞中,發(fā)現(xiàn)解決旋轉(zhuǎn)問題的根本是抓住旋轉(zhuǎn)不變性。從發(fā)現(xiàn)、提出問題,到分析、解決問題,都由學(xué)生主導(dǎo)。隨后,教師可引導(dǎo)學(xué)生總結(jié)、歸納其中的思想方法,挖掘其本質(zhì)。
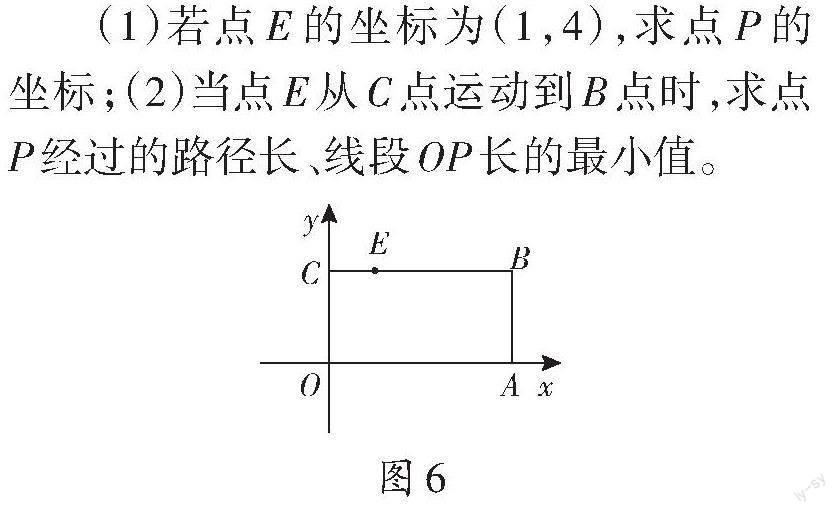
問題3 如圖6,在矩形ABCO中,點B坐標為(8,4),點E是線段CB上一動點,以點E為旋轉(zhuǎn)中心,把線段EA繞點E逆時針旋轉(zhuǎn)90[°],點A的對應(yīng)點為點P。
(1)若點E的坐標為(1,4),求點P的坐標;(2)當點E從C點運動到B點時,求點P經(jīng)過的路徑長、線段OP長的最小值。
4. 總結(jié)反思
最后,教師引導(dǎo)學(xué)生從這幾個方面進行總結(jié):如何研究圖形的旋轉(zhuǎn)?關(guān)于圖形的旋轉(zhuǎn)主要研究哪些問題?怎樣進行研究?研究圖形旋轉(zhuǎn)時要注意采取哪些思想方法?類比圖形的選擇,在解決圖形的變換的問題時,你有哪些想法?
【設(shè)計意圖】旋轉(zhuǎn)中心由定到動進行變化,學(xué)生在分析過程中,發(fā)現(xiàn)解決旋轉(zhuǎn)問題的根本仍是抓住不變性,同時發(fā)現(xiàn)可以用函數(shù)的思想解決問題。該問題的設(shè)計促成了問題教學(xué)的“閉環(huán)”。通過問題3,了解學(xué)生的學(xué)習(xí)情況,本節(jié)課達成了預(yù)期效果。最后的總結(jié)反思幫助學(xué)生進一步梳理、完善和強化所學(xué)習(xí)的知識,也對問題的解決進行最后的深化。
三、教學(xué)反思
數(shù)學(xué)學(xué)習(xí)必須有問題,沒有問題無法學(xué)好數(shù)學(xué)。在學(xué)習(xí)過程中,打破慣性思維和惰性思維,進行不斷質(zhì)疑產(chǎn)生的新思想才是學(xué)生真正的收獲。在此過程中,學(xué)生的創(chuàng)新意識也在加強,所以,創(chuàng)新教育實際上是以培養(yǎng)學(xué)生問題意識作為起點的。
本節(jié)課,筆者從日常的汽車雨刮器的轉(zhuǎn)動情境中,引導(dǎo)學(xué)生用數(shù)學(xué)的眼光觀察世界。學(xué)生在自主思考中復(fù)習(xí)了畫旋轉(zhuǎn)圖形的方法、旋轉(zhuǎn)的本質(zhì)、關(guān)于旋轉(zhuǎn)的結(jié)論。通過沒有條件的旋轉(zhuǎn)能得到哪些結(jié)論?學(xué)生自由思考。每個學(xué)生都是從自身的已有知識經(jīng)驗和生活經(jīng)驗出發(fā)理解新事物的,因此,不同學(xué)生對于同一個情境可以提出不同的問題。當學(xué)生的思維自由發(fā)散時,他們原有的知識和經(jīng)驗與新的學(xué)習(xí)內(nèi)容之間就很容易發(fā)生“沖突”,這個“沖突”就是問題形成的基礎(chǔ)。如果讓學(xué)生產(chǎn)生興趣是問題教學(xué)開展的前提,那么讓學(xué)生自由呈現(xiàn)“沖突”和問題則是問題教學(xué)的關(guān)鍵。一題多變、 一題多解可以幫助學(xué)生呈現(xiàn)對同一問題的不同思考。學(xué)生在各種“沖突”中,通過研究,關(guān)注到旋轉(zhuǎn)的不變性,發(fā)現(xiàn)了解決旋轉(zhuǎn)問題的根本是抓住旋轉(zhuǎn)不變性,哪怕旋轉(zhuǎn)中心由定到動變化,解決旋轉(zhuǎn)問題的根本仍是抓住不變性。通過對問題的“閉環(huán)”設(shè)計,深化對問題的思考和研究;通過對“沖突”的分析和總結(jié),提煉解決問題的思想和方法。
本文系江蘇省南京市教育科學(xué)“十四五”規(guī)劃課題“指向核心素養(yǎng)的初中數(shù)學(xué)問題教學(xué)實踐研究”(課題編號:JZ/2021/058)階段性研究成果。
(作者單位:南京師范大學(xué)附屬中學(xué)江寧分校)

