嵌入式共固化縫合阻尼復合材料面內彈性參數(shù)

劉昭陽,梁 森,孫瑞駿,羅 皓,胡子健,朱 笛

(青島理工大學 機械與汽車工程學院, 山東 青島 266520)

0 引言

嵌入式共固化縫合阻尼復合材料(ECSDC)是由多種的不同性質的材料以共固化工藝通過物理或化學的方法形成的多相固體。復合材料板中的基體相、面內增強相和粘彈性阻尼材料在性能上相互協(xié)調,從而得到單一材料所不能企及的良好的阻尼性能和綜合力學性能。纖維縫線對上、下樹脂增強纖維蒙皮夾鉗阻尼結構進行縫合,在共固化工藝時,蒙皮中的樹脂會沿縫合線流動貫穿整個復合材料層間結構形成復合釘。該特殊結構作為z方向的增強相能夠有效地增強復合材料的力學性能和層間剪切性能,使新結構具有三向力學可設計性的優(yōu)點,利于該結構在精密儀器制造、航空航天等領域的推廣。

在研究胞元材料的面內等效彈性參數(shù)方面,文獻[1-3]中用理論近似法建立了胞元結構面內等效彈性參數(shù)的理論分析模型。Dos Reis和Ganghoffer[4]、Arabnejad與Pasini[5]采用漸近均質法(asymptotic homogenization,AH)獲得了周期性胞元結構的面內等效彈性參數(shù)。Lainé等采用代表體積單元法(representative volume element method,RVE)分析了胞元夾芯結構的橫向剪切剛度[6]。文獻[7-10]中給出了圓柱狀蜂窩胞元、六邊形胞元、梯形胞元、方形胞元的等效彈性模量解析方程,并采用有限元方法(finite element method,FEM)驗證了理論模型的有效性。文獻[11-14]中研究了點陣結構的面內等效彈性參數(shù)。

在研究阻尼薄膜夾嵌復合材料性能方面,潘利劍等[15]使用結合的模態(tài)應變能法和模態(tài)疊加法,分析了連續(xù)阻尼薄膜夾嵌復合材料的阻尼性能。Arikoglu與Ozkol等[16]將一階剪切變形理論(first-order shear deformation theory,FSDT)與廣義微分求積法相結合,對阻尼薄膜夾嵌復合材料板進行了動力學分析。路慶賀等[17]使用FSDT和Hamilton原理,推導了阻尼夾芯復合材料加筋板的應變能、動能公式,并使用變分原理建立了該結構的控制微分方程。王紹清等[18-19]根據(jù)Rayleigh-Ritz法計算了單層與多層阻尼薄膜夾嵌復合材料帶筋結構的損耗因子和模態(tài)頻率,并對結構進行了優(yōu)化設計。閆盛宇等[20]開發(fā)了ECSDC板的制作工藝,為測試該結構的抗拉伸性能、層間剪切性能和阻尼性能,搭建了例如層間剪切試驗、拉伸破壞試驗、自由衰減試驗等的試驗平臺,為ECSDC以后更深入的研究奠定了基礎。

目前國內外鮮有文獻對縫合纖維阻尼復合材料胞元結構的面內等效彈性參數(shù)的問題進行研究,這將阻礙對ECSDC結構的繼續(xù)研究與應用推廣。為此本文中通過建立ECSDC中復合釘貫通的面內纖維折線變形模型,探索該結構的面內等效彈性參數(shù)問題。由于復合釘貫通整個層合結構,上、下蒙皮的彈性參數(shù)未知,因此從復合釘貫通的纖維增強阻尼薄膜的面內等效彈性參數(shù)計算入手,過渡到ECSDC。使用ANSYS和Matlab研究ECSDC典型結構,將理論預測數(shù)據(jù)與模擬預測數(shù)據(jù)和文獻值相比較,驗證該理論模型的準確性,為ECSDC結構的動力學研究及使用推廣提供理論依據(jù)。

1 縫合阻尼復合材料的面內等效彈性參數(shù)

由于復合釘貫通了縫合阻尼復合材料的整個層合結構,且上、下蒙皮的彈性參數(shù)未知。因此,先從縫合纖維增強阻尼薄膜的面內等效彈性參數(shù)計算入手,過渡到ECSDC。

1.1 基本假設

采用改進鎖式縫合方式[21]的ECSDC結構如圖1所示,建立的x-y-z宏觀結構笛卡爾坐標系如圖2所示。

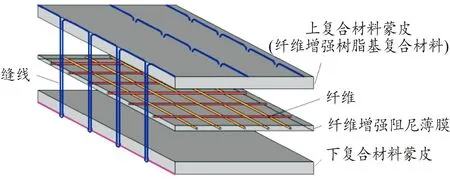
圖1 采用改進的鎖式縫合方式的ECSDC示意圖

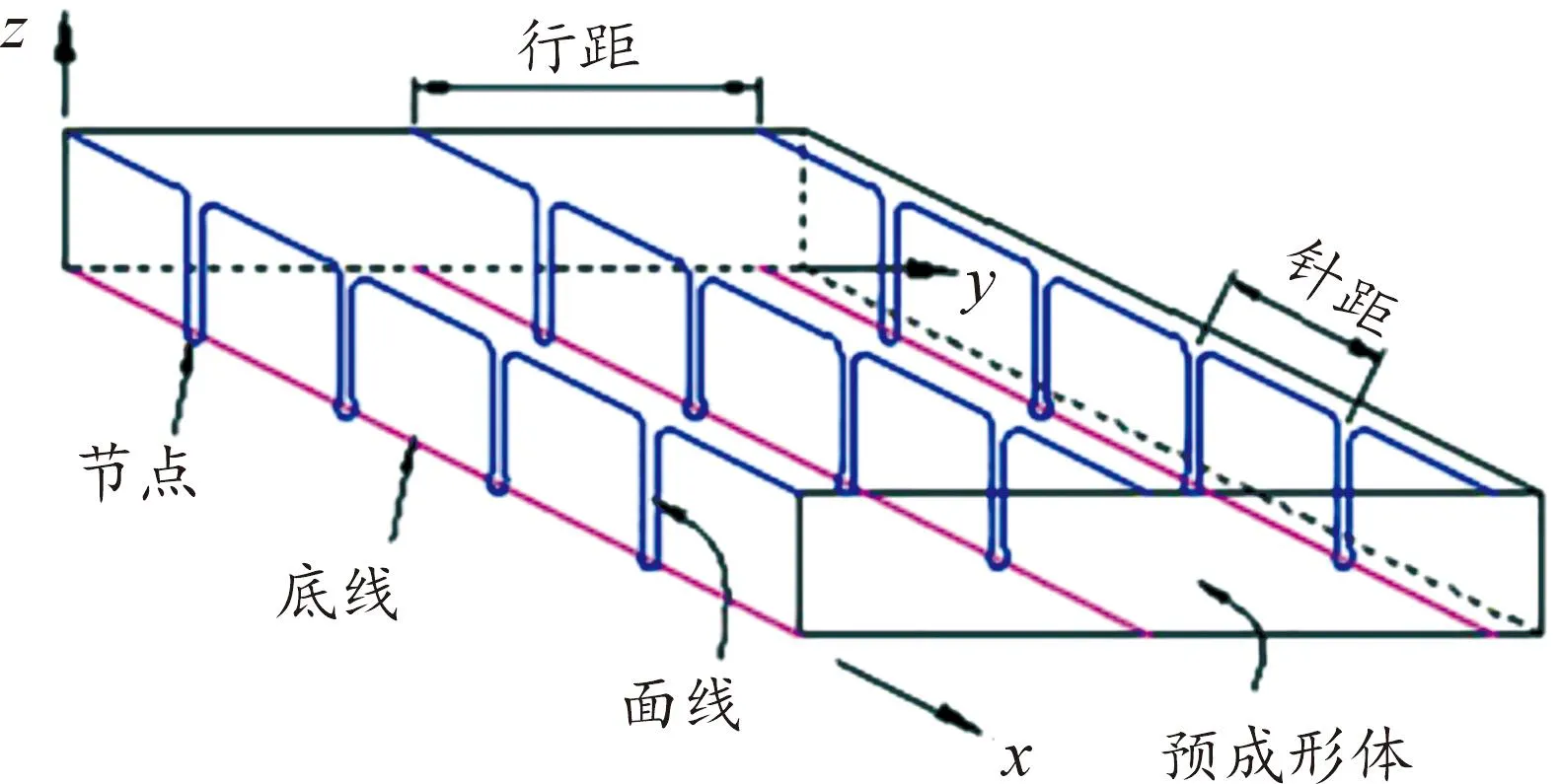
圖2 笛卡爾坐標系示意圖

為方便建模,假設如下:

1) 忽略纖維在針孔附近的局部損傷;

2) 底線與面線均不會發(fā)生卷曲,在縫合與固化工藝之后仍然保持圓形截面;

3) 在縫合之前,經紗與緯紗均為直線,縫合后仍然是直線;

4) 經紗變形區(qū)的緯紗不發(fā)生變形,緯紗變形區(qū)的經紗不發(fā)生變形;

5) 忽略縫合后纖維之間的拉伸-彎曲以及拉伸-剪切耦合影響。

若將縫合纖維阻尼薄膜視為周期性結構且每個周期內的纖維變形不發(fā)生改變,那么可以選取一個胞元結構建立復合釘貫通的面內纖維折線變形模型(如圖3所示)。其中行距(L)定義為2行縫線之間的距離,針距(N)定義為同一行縫線上2個相鄰針孔的中心距;η1-η2-η3為胞元結構的局部坐標系。因為胞元結構的對稱性,為簡化模型選取1/4的胞元(如圖4所示)進行研究。

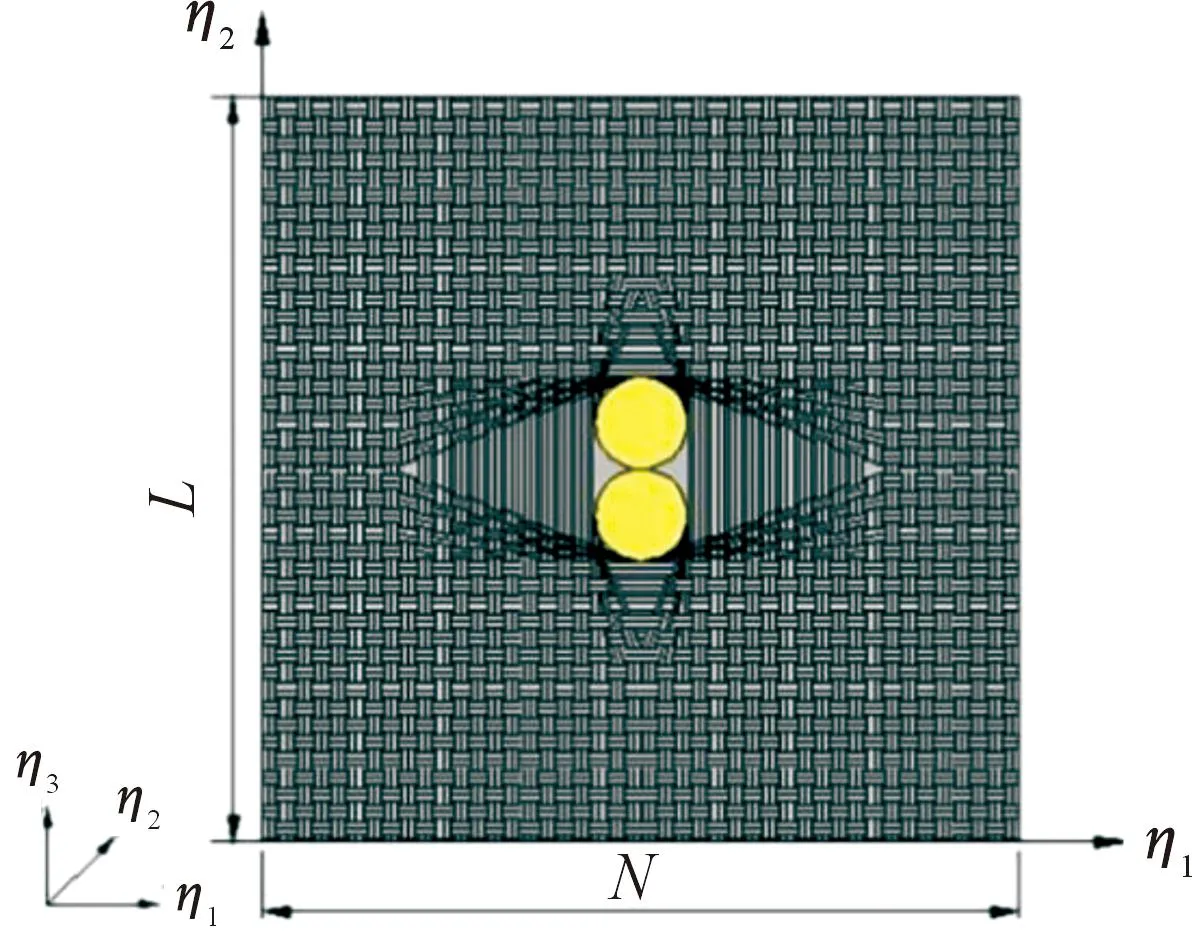
圖3 復合釘貫通的面內纖維折線變形模型

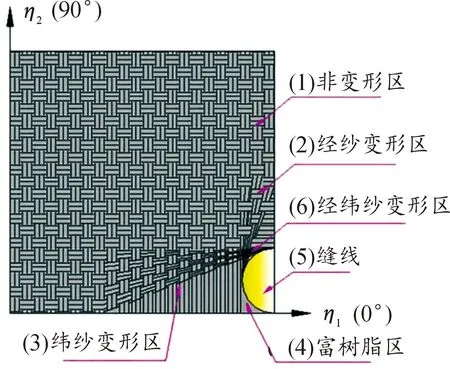
圖4 1/4胞元結構

因為復合釘?shù)牟迦雽е吕w維增強阻尼薄膜的面內力學性能分布不均,接下來將分析每個區(qū)域(已在圖4中標號劃定)的彈性參數(shù)。

1.2 非變形區(qū)的面內等效彈性參數(shù)

縫合纖維增強阻尼薄膜非變形區(qū)的主要成分是纖維和阻尼材料,材料坐標系如圖5所示。

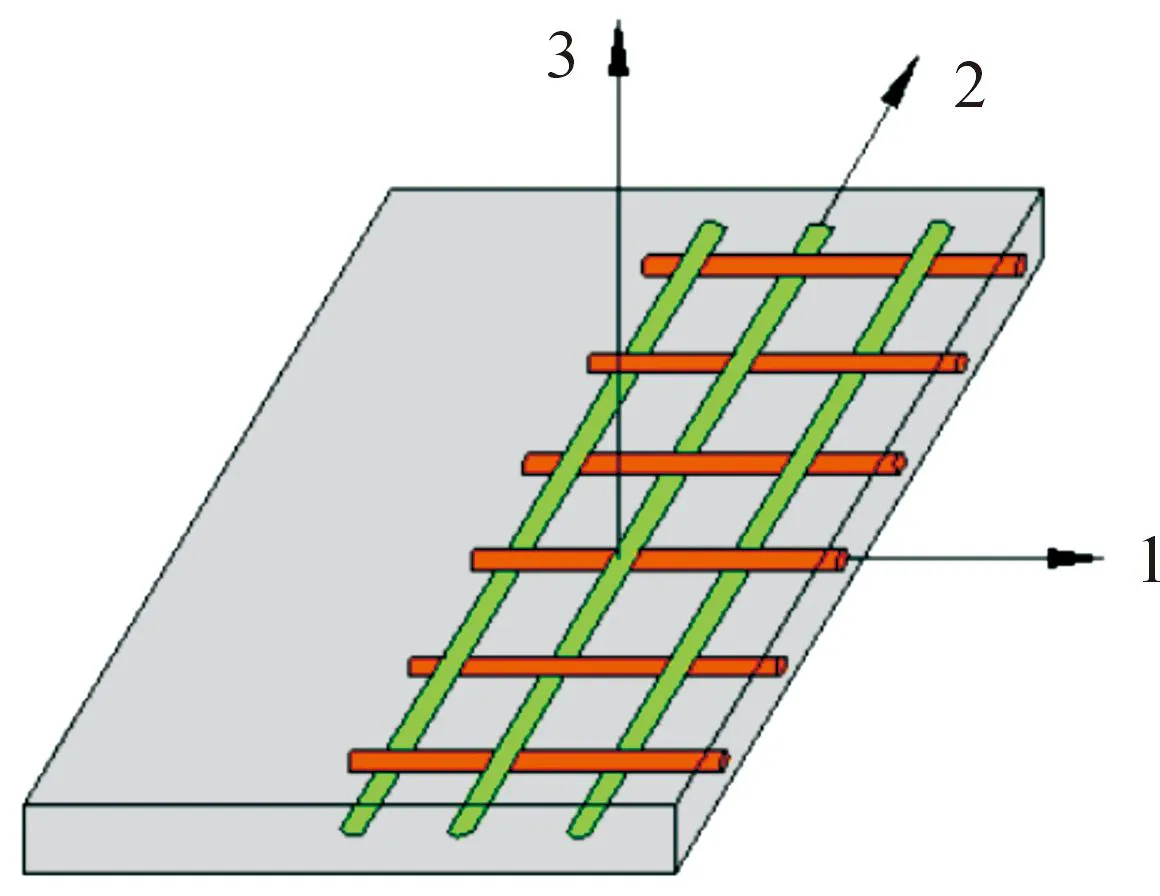
圖5 平紋編織纖維的坐標軸

根據(jù)文獻[22]可得到經紗單向板和緯紗單向板的彈性參數(shù):

Em={E1,m,E2,m,G12,m,ν21,m,ν12,m}

(1)

式(1)中:m為單向板,當m=j、w時分別表示經紗單向板、緯紗單向板;E1,m、E2,m分別為單向板在材料1軸、2軸的彈性模量,GPa;G12,m為單向板在1-2平面內的剪切模量,GPa;ν21,m、ν12,m為單向板的泊松比。

平紋編織阻尼基復合材料的彈性參數(shù)表達式為:

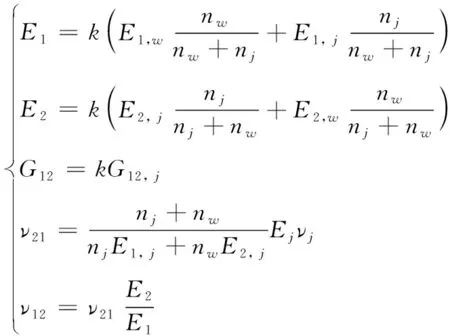
(2)

式(2)中:E1和E2分別為材料坐標系1軸、2軸的彈性模量,GPa;G12為1-2平面內的剪切模量,GPa;和是泊松比;ν12和ν21分別為平紋編織單層板中緯紗和經紗的相對含量。

對于變形區(qū)而言,復合釘周圍的纖維會發(fā)生一定程度的偏轉。縫合纖維增強阻尼薄膜的鋪層角度θ對纖維偏轉的影響可近似認為是0°鋪層下纖維偏轉之后再旋轉角度θ。

在非變形區(qū),材料主軸與局部坐標軸平行,即:夾角θ(1)=0。該區(qū)域的彈性參數(shù)根據(jù)式(1)—式(2)獲得:

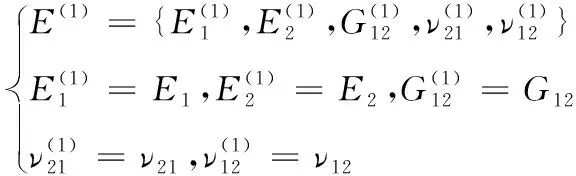
(3)

式(3)中,上標(1)表示非變形區(qū)的區(qū)域編號。

1.3 經紗變形區(qū)的面內等效彈性參數(shù)

應力-應變關系為(應力單位:GPa):

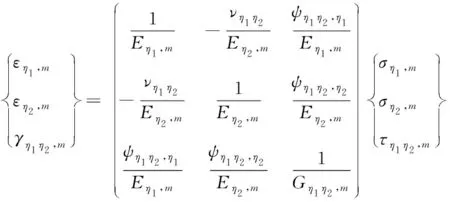
(4)

其中:

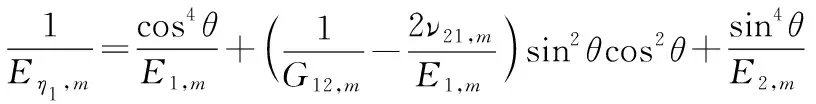
(5)

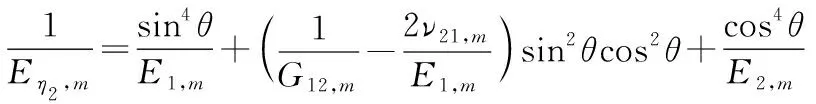
(6)

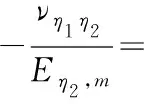
(7)

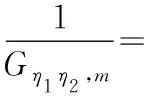
(8)

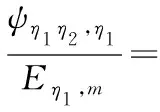
(9)

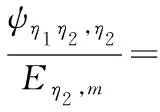
(10)

如圖6、圖7所示,經紗纖維的偏轉變形程度隨位置和縫合方向的變化而變化。

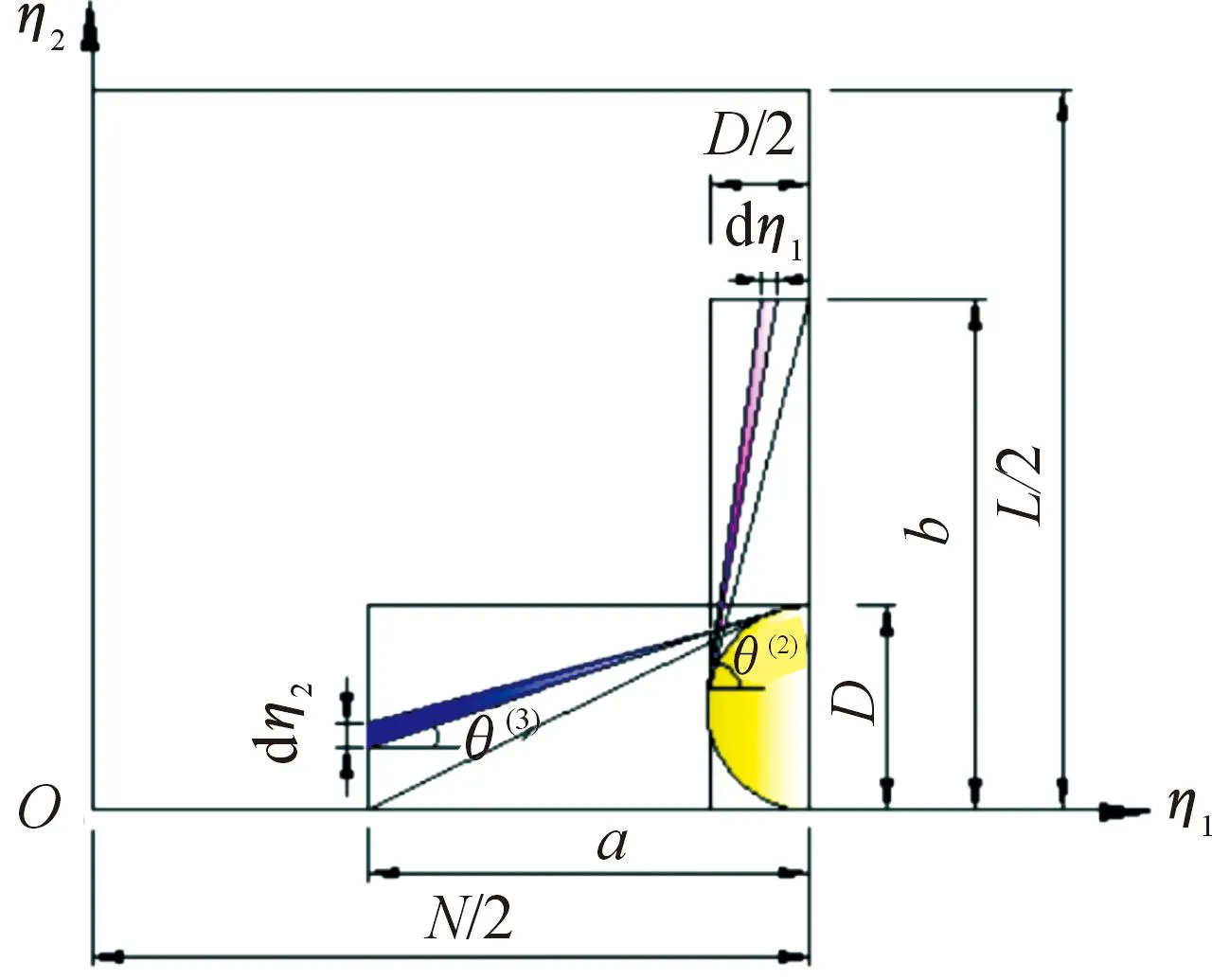
圖6 縫合方向平行于x軸的折線變形模型

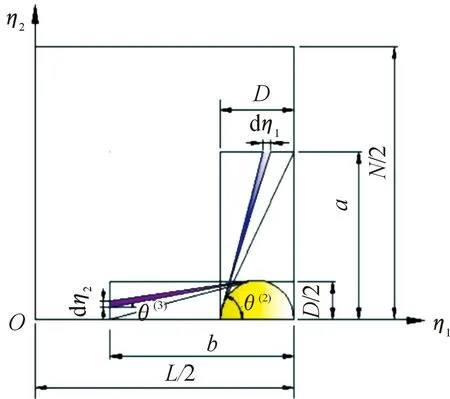
圖7 縫合方向平行于y軸的折線變形模型

當縫合方向平行于x軸時,經紗纖維與η1軸的夾角θ(2)可表示為:

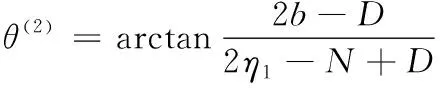
(11)

當縫合方向平行于y軸,θ(2)可表示為:

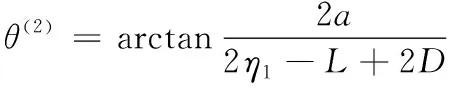
(12)

其中:b和a分別代表縫合方向平行于x軸和y軸時經紗變形區(qū)的長度。

將經紗偏轉角θ(2)代入式(5)—式(10),可得到經紗微帶dη1的彈性參數(shù)。

當縫合方向平行于x軸時,將式(11)代入式(5)—式(10),有:

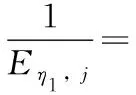
(13)

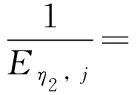
(14)

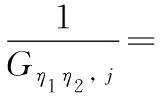
(15)

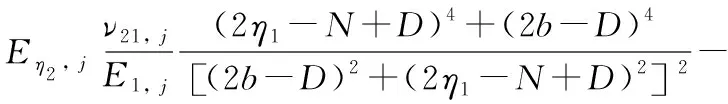
(16)

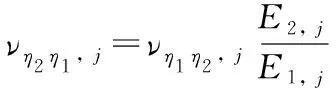
(17)

由式(1)可得:

Ej={E1, j,E2, j,G12, j,ν21, j,ν12, j}

(18)

且該區(qū)域內經紗的平均彈性參數(shù)為:

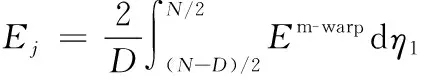
(19)

式(19)中:上標m-warp表示經紗微帶dη1,且有:

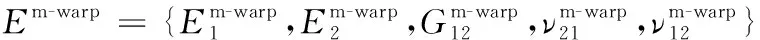
(20)

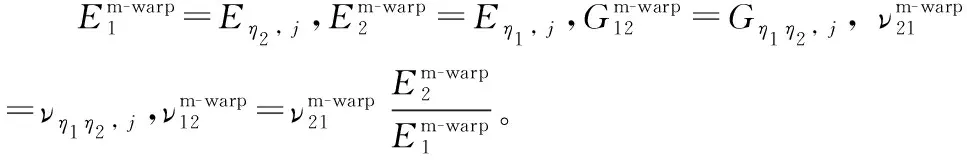
當縫合方向平行于y軸,將式(12)代入式(5)—式(10),有:

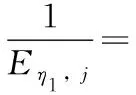
(21)

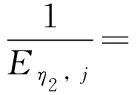
(22)

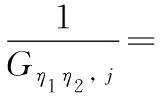
(23)

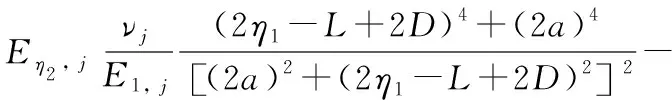
(24)

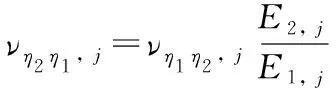
(25)

該區(qū)域經紗的平均彈性參數(shù)為:

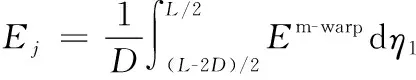
(26)

由式(1)可得到在經紗變形區(qū)的緯紗彈性參數(shù):

Ew={E1,w,E2,w,G12,w,ν21,w,ν12,w}

(27)

將經紗和緯紗的彈性參數(shù)代入式(2)得到經紗變形區(qū)的彈性參數(shù):

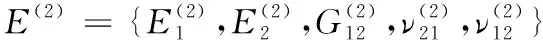
(28)

式(28)中:上標(2)表示經紗變形區(qū)的區(qū)域編號。

1.4 緯紗變形區(qū)的面內等效彈性參數(shù)

緯紗纖維變形段與η1軸之間的夾角θ(3)隨坐標η2的增大而減小。

當縫合方向平行于x軸時,有:

(29)

當縫合方向平行于y軸時,有:

(30)

將經紗偏轉角θ(3)代入式(5)—式(10),可得到緯紗微帶dη2的彈性參數(shù)。

當縫合方向平行于x軸時,將式(29)代入式(5)—式(10),有:

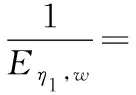
(31)

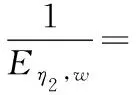
(32)

式(31)—式(32)中:E1,w、E2,w、G12,w與v21,w可由式(1)獲得。

該區(qū)域內緯紗的平均彈性參數(shù)為:

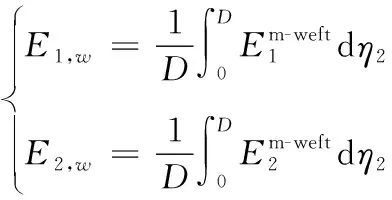
(33)

式(33)中:上標m-weft表示緯紗微帶dη2,且有:

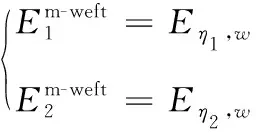
(34)

當縫合方向平行于y軸時,將式(30)代入式(5)—式(10),有:

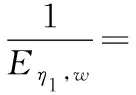
(35)

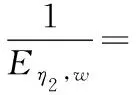
(36)

該區(qū)域內緯紗的平均彈性參數(shù)為:

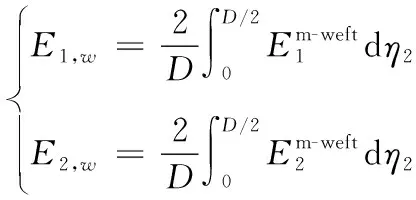
(37)

根據(jù)第4條假設,在該區(qū)域內經紗的彈性參數(shù)可由式(1)得到,有:

Ej={E1, j,E2, j,G12, j,ν21, j,ν12, j}

(38)

將經紗與緯紗的彈性參數(shù)代入式(2),獲得緯紗變形區(qū)的彈性參數(shù),有:

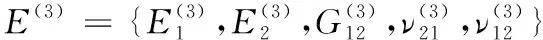
(39)

式(39)中:上標(3)代表緯紗變形區(qū)的區(qū)域編號。

1.5 富樹脂區(qū)的面內等效彈性參數(shù)

富樹脂區(qū)內主要是在復合材料共固化時填充了縫線與增強纖維之間空隙的樹脂,因此可以看作各向同性材料,該區(qū)域的彈性參數(shù):

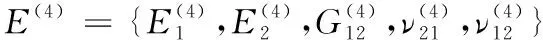
(40)

其中:上標(4)代表富樹脂區(qū)的區(qū)域編號,且:

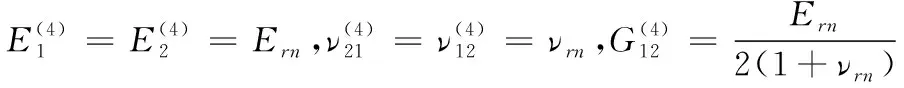
(41)

式(41)中:下標rn表示樹脂。

1.6 縫線的面內等效彈性參數(shù)

縫線區(qū)需考慮縫線的橫向強度,因此:

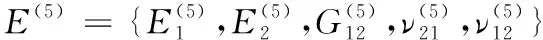
(42)

其中:上標(5)代表縫線區(qū)的區(qū)域編號,并且:

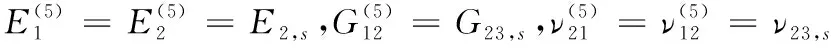
(43)

式(43)中:下標s表示縫線。

1.7 經緯紗變形區(qū)的面內等效彈性參數(shù)

在該區(qū)域內,經紗與緯紗均發(fā)生偏轉。當縫合方向平行于x軸時,將式(18)與式(33)代入式(2);當縫合方向平行于y軸時,式(27)與式(37)代入式(2),有:

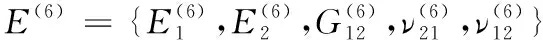
(44)

其中:上標(6)代表經緯紗變形區(qū)的區(qū)域編號。

1.8 縫合纖維增強阻尼薄膜的面內等效彈性參數(shù)

根據(jù)混合定理,獲得胞元結構的面內等效彈性參數(shù)。由于胞元結構的平均屬性可以描述宏觀結構的有效屬性,因此,縫合纖維增強阻尼薄膜的彈性參數(shù)為:

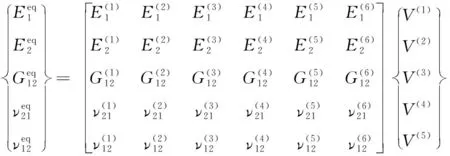
(45)

其中:上標eq表示面內等效彈性參數(shù);是每個區(qū)域的相對體積分數(shù),可得:

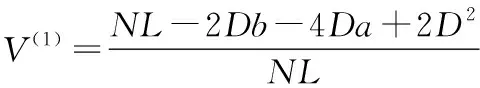
(46)

(47)

(48)

(49)

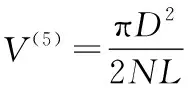
(50)

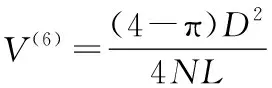
(51)

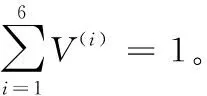
1.9 縫合阻尼復合材料的面內等效彈性參數(shù)

在ECSDC中,有復合釘貫通的上、下蒙皮的面內等效彈性參數(shù)可參照縫合纖維增強阻尼薄膜的數(shù)學模型,只需把模型中阻尼材料替換為樹脂,由式(45)可得:

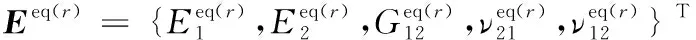
(52)

其中:Eeq(r)為第r層的等效彈性參數(shù)矩陣,r=1,2,3;r=1、3時為上、下蒙皮的彈性參數(shù),r=2時為縫合纖維增強阻尼薄膜的彈性參數(shù)。

ECSDC第r層的應力-應變關系可寫為:

ε(r)=S(r)σ(r)

(53)

其中:將第r層的鋪層角度σ(r)和Eeq(r)矩陣中的元素代入式(11)—式(12),可獲得第r層的柔度矩陣S(r)。

由文獻[22]建立ECSDC的面內等效彈性參數(shù)模型。ECSDC的本構關系表達式為:

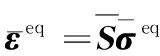
(54)

ECSDC中任一點的面內應力可通過均質化法[22]進行定義,即:

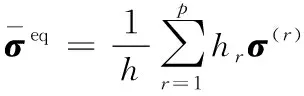
(55)

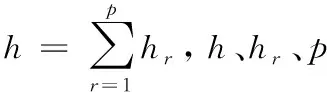
假設ECSDC的各層都經歷了相同的面內應變,則:

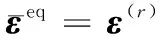
(56)

將式(52)、式(53)、式(55)與式(56)代入式(54),縫合層合板的柔度矩陣可以借助每一層的柔度矩陣進行表示,即:

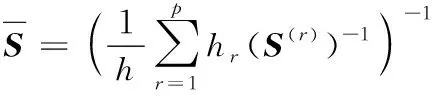
(57)

由式(57)即可獲得ECSDC的面內等效彈性參數(shù)。

2 理論模型驗證

為驗證所推公式的準確性,首先將理論模型與ANSYS有限元軟件模擬進行比較。選取長×寬為250 mm×25 mm且縫線間距為10 mm的ECSDC梁試件進行建模,試件總厚度為2.1 mm。在ANSYS軟件中以SOLID185單元建立ECSDC模型,各復合材料層之間使用共節(jié)點進行連接。

上、下樹脂增強蒙皮是玻纖/酚醛復合材料預浸料,上下層厚度為各1 mm,材料參數(shù)由文獻[23]所得,如表1、表2所示;夾嵌的纖維增強阻尼薄膜是將平紋編織纖維布預浸阻尼溶液后壓制而成,纖維布材料參數(shù)接近粘彈性材料,阻尼材料采用丁腈橡膠,該層厚度為0.1 mm,材料參數(shù)如表3、表4所示。縫線選取Kevlar-49,其材料參數(shù)由表5給出。

表1 玻纖/酚醛復合材料參數(shù)

表2 酚醛樹脂材料參數(shù)

表3 平紋編織纖維布/丁腈橡膠材料參數(shù)

表4 丁腈橡膠粘彈性阻尼材料參數(shù)

表5 芳綸纖維參數(shù)

由于縫線相對其他結構要細的多,為方便芳綸纖維的建模,將其橫截面簡化為正方形,以纖維密度為1.44 g/cm3的1 500旦芳綸纖維為例,其纖維橫截面積為0.12 mm2,故其簡化后的正方形邊長為0.346 4 mm。建模后的ECSDC梁試件如圖8所示。

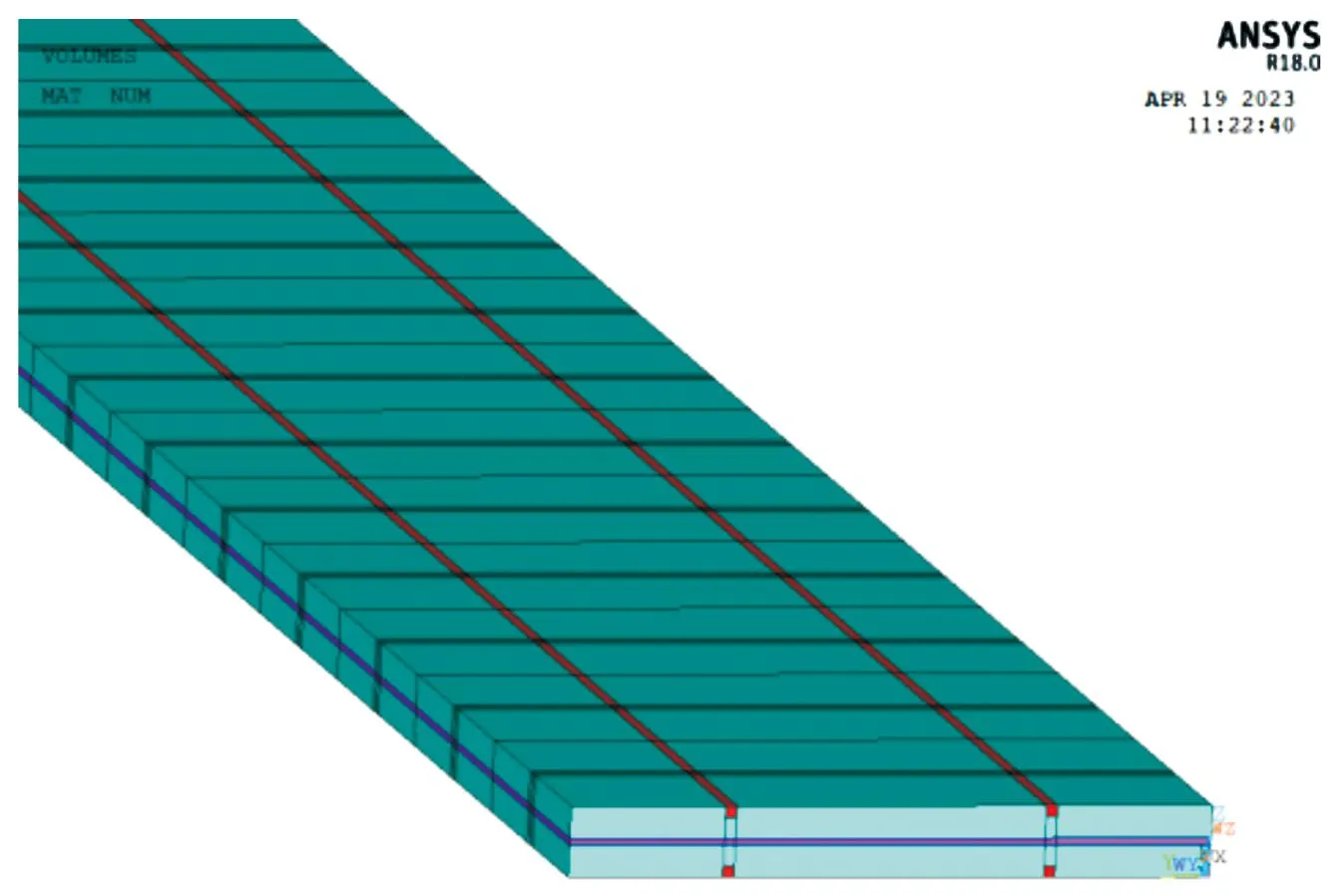
圖8 建立的ECSDC梁試件模型

分別對縫合針距為8、10、12 mm的ECSDC梁試件的彈性參數(shù)進行ANSYS數(shù)值模擬計算,其中針距10 mm的ECSDC梁試件應力、應變如圖9、圖10所示。將理論模型在Matlab軟件環(huán)境中編程,計算相同縫合針距的理論結果。結合文獻[24]中試驗所得相同縫合針距的彈性參數(shù),將3種方式得到沿x軸方向的等效彈性模量E1在表6中列出,分別計算理論值與其他2種結果的相對誤差并取絕對值。通過比較可以看出,3種方法得到的計算結果較為相近,相對誤差均在5%以內,可以認為該理論模型是較為準確的。

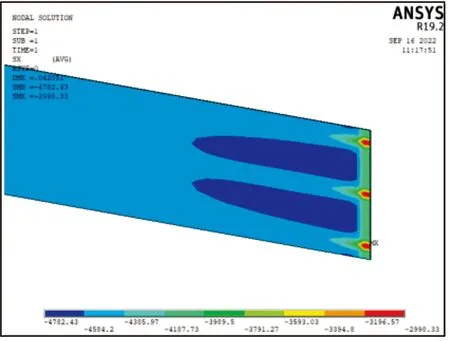
圖9 ECSDC梁試件的應力云圖

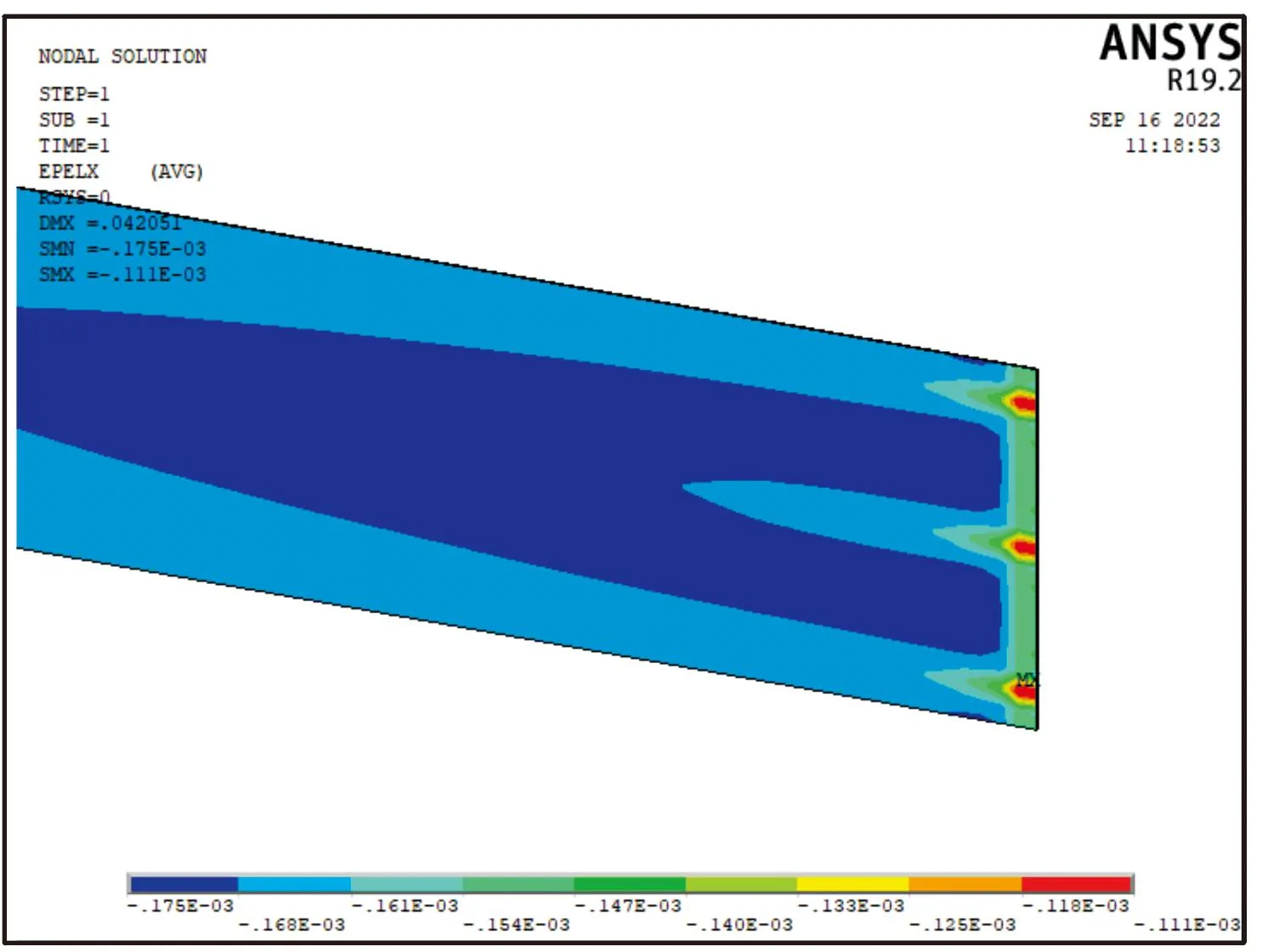
圖10 ECSDC梁試件的應變云圖

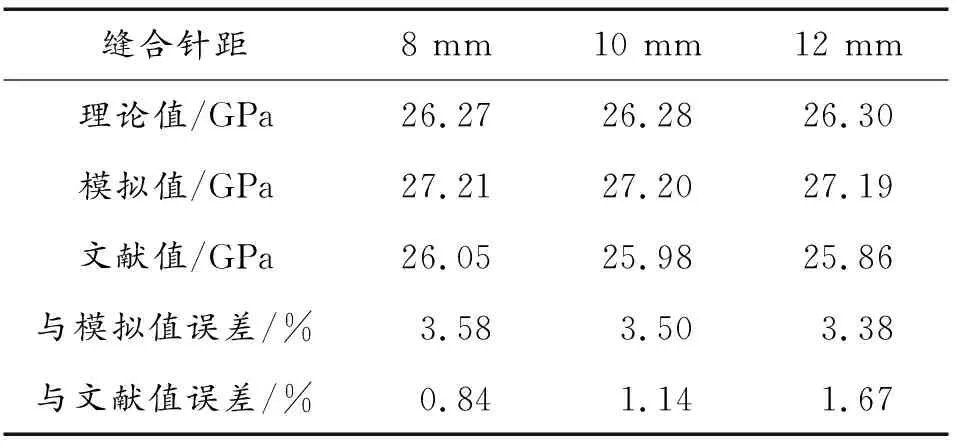
表6 理論計算與數(shù)值模擬、文獻實驗的結果比較

出現(xiàn)誤差的主要原因:一是理論模型在計算時僅考慮了富樹脂區(qū)和面內纖維偏轉等因素,而文獻中的試驗還會受到如纖維損傷等因素影響;二是在有限元建模時對縫線進行了模型簡化處理,且有限元模擬時不會考慮上述因素的作用。

3 設計參數(shù)對結構等效彈性參數(shù)的影響

基于已經驗證的理論模型,進一步探討縫合密度、縫線直徑、鋪層角度及縫合方向等設計參數(shù)的變化對ECSDC整體結構面內等效彈性參數(shù)的影響,揭示縫合工藝對結構各向異性的影響。

3.1 縫合密度的影響

由縫合密度的定義可知:縫合密度=1/(針距×行距)。通過改變針距和行距,研究縫合密度對結構面內等效彈性參數(shù)的影響。

保持模型的結構總尺寸、縫線行距、縫線直徑及鋪層角度等因素不變,研究縫合針距對結構面內等效彈性參數(shù)的影響。引入變化率這一概念:變化率=(縫合結構的彈性參數(shù)—未縫合結構的彈性參數(shù))/未縫合結構的彈性參數(shù)。其變化曲線如圖11和圖12所示。

由變化曲線圖可知,相較于未縫合結構(變化率為0),ECSDC 的面內等效彈性參數(shù)有所降低。當縫合針距相對較小時,ECSDC 結構彈性模量和剪切模量的降低比較明顯,而隨著縫合針距的增大,彈性模量和剪切模量逐漸趨于未縫合結構的彈性參數(shù)。即當縫線行距不變時,結構的面內等效彈性參數(shù)隨縫合針距的減小而降低;另外,當縫合方向平行于x軸時,彈性模量E1的變化率比E2的變化率小;當縫合方向沿著y軸時,彈性模量E2的變化率比E1的變化率小,這表明縫合工藝提高了結構的各向異性。

圖11 面內等效彈性參數(shù)與縫合針距的變化關系 (縫合方向平行于x軸)

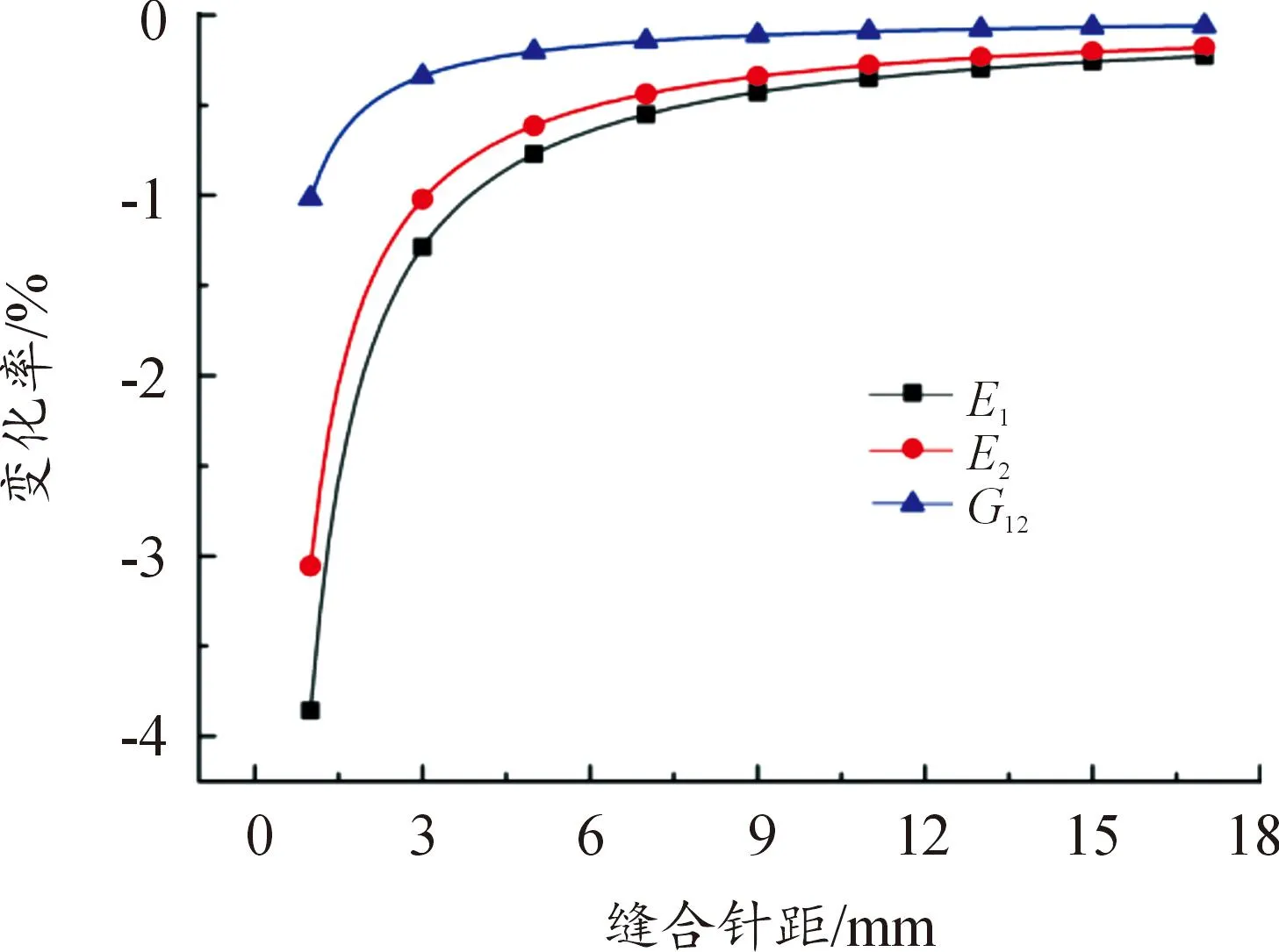
圖12 面內等效彈性參數(shù)與縫合針距的變化關系 (縫合方向平行于y軸)

保持模型的結構總尺寸、縫合針距、縫線直徑及鋪層角度等因素不變,研究縫線行距對結構面內等效彈性參數(shù)的影響。得到的變化率曲線如圖13和圖14所示。

由變化曲線圖可知:縫線行距對面內等效彈性參數(shù)的影響類似于縫合針距,即當縫合針距不變時,結構的面內等效彈性參數(shù)隨縫合行距的減小而降低;另外,改變縫合方向后彈性模量E1和E2的變化率差異也表明了縫合工藝對結構各向異性的增強作用。

由縫合密度的定義,可以進一步得到以下結論:當縫線直徑和鋪層角度不變,ECSDC 結構的面內等效彈性參數(shù)會隨縫合密度的增大而降低。原因包括2個方面:一是纖維彎曲會降低纖維的軸向力學性能,不同的縫合密度將導致纖維發(fā)生不同程度的偏轉變形;二是富樹脂區(qū)的布局差異會造成局部應力集中,從而降低結構的力學性能。縫合密度越大意味著富樹脂區(qū)和發(fā)生偏轉變形的纖維占比越大。

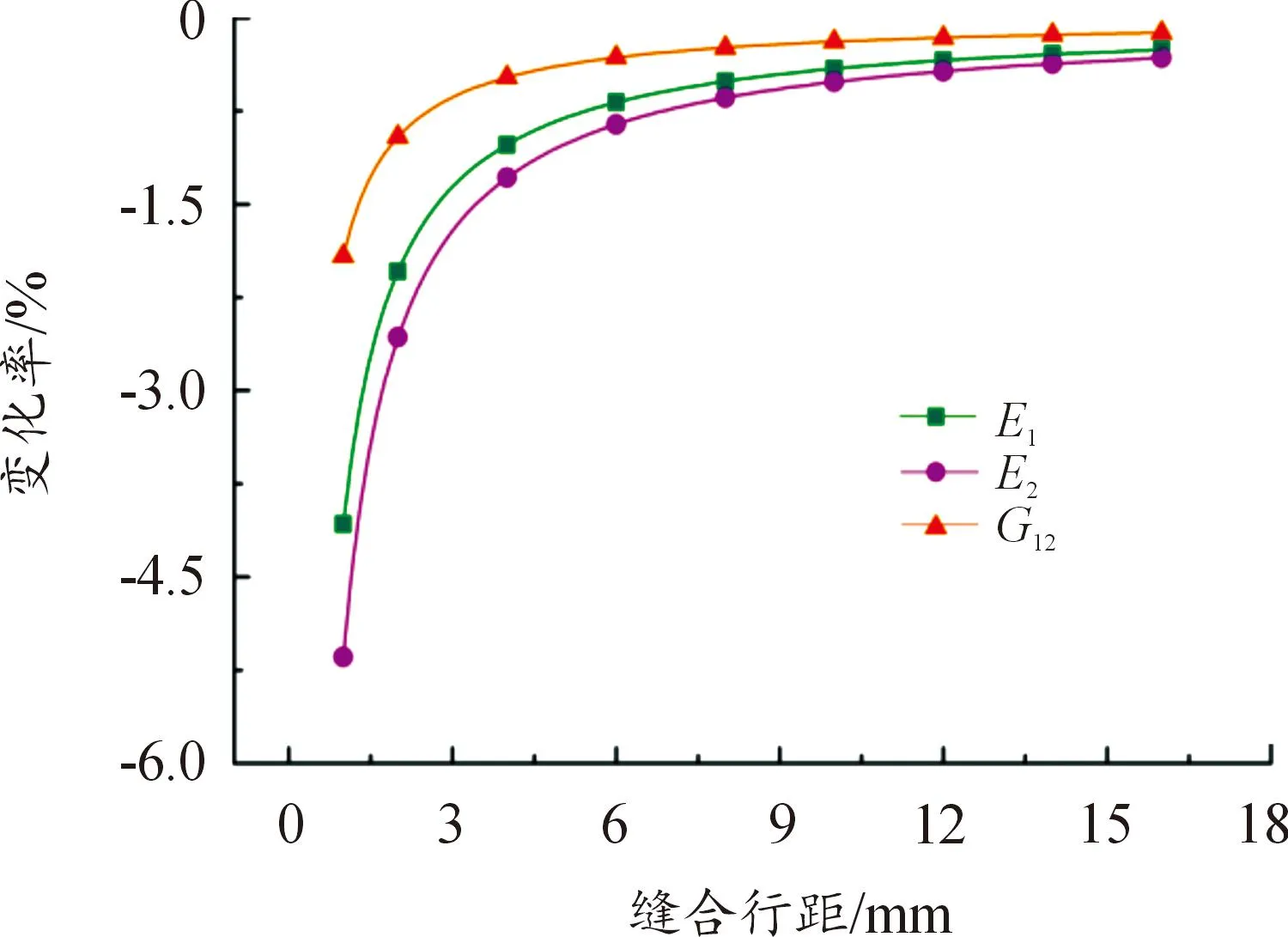
圖13 面內等效彈性參數(shù)與縫線行距的變化關系 (縫合方向平行于x軸)

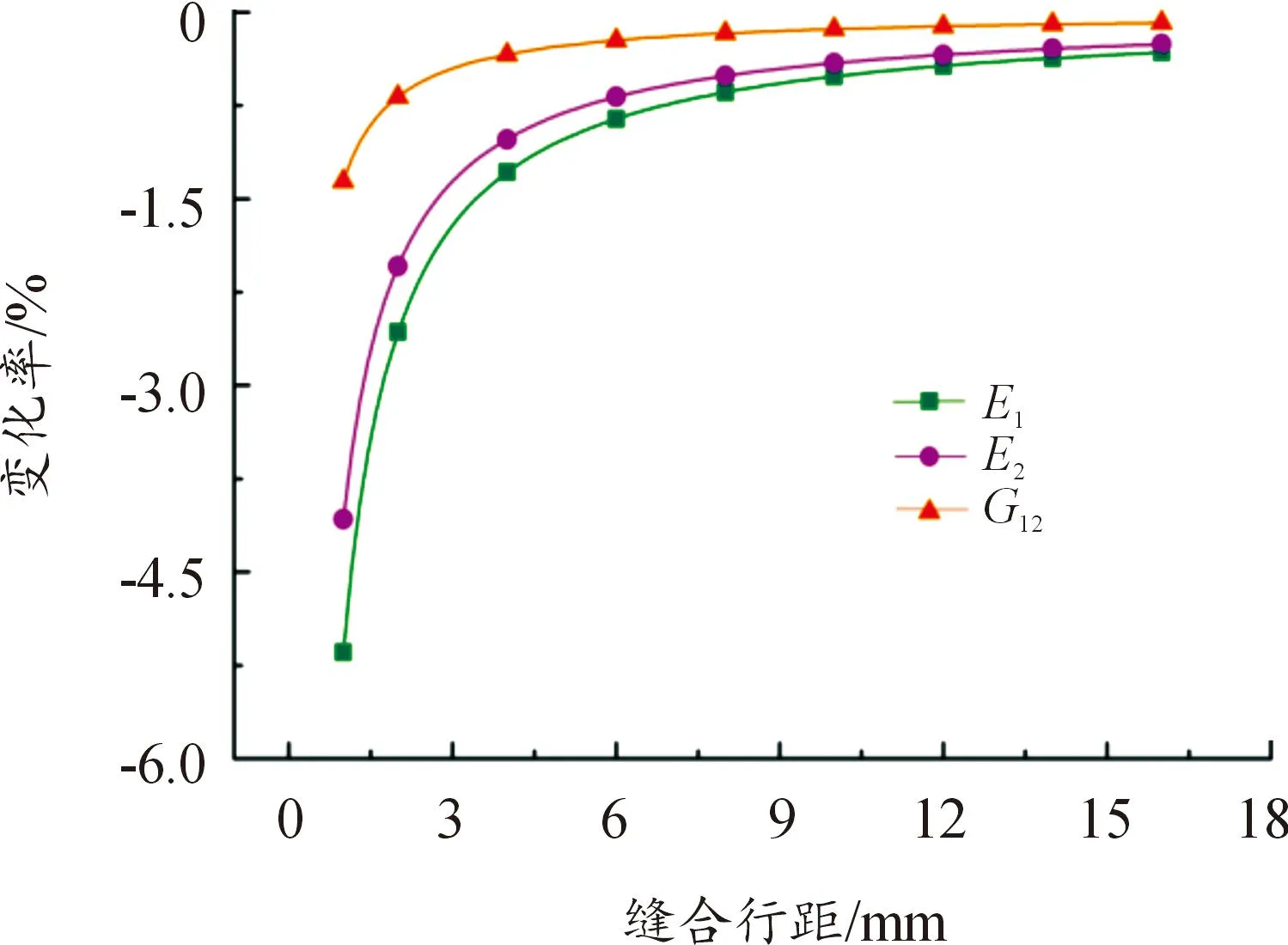
圖14 面內等效彈性參數(shù)與縫線行距的變化關系 (縫合方向平行于y軸)

3.2 縫線直徑的影響

保持模型的結構總尺寸、縫合針距、縫線行距和鋪層角度等因素不變,且縫合方向始終平行于x軸,研究縫線直徑對結構面內等效彈性參數(shù)的影響。得到的變化率曲線如圖15所示。

由圖15可知,當縫合針距與縫線行距不變,ECSDC 結構的彈性模量和剪切模量隨縫線直徑的增大而降低。主要原因是隨著縫線直徑的增大,面內纖維的偏轉角增大,同時富樹脂區(qū)的面積也增大,從而對結構面內等效彈性參數(shù)產生影響。

3.3 鋪層角度的影響

保持模型的結構總尺寸、縫合針距、縫線行距和縫線直徑等因素不變,且縫合方向始終平行于x軸,研究鋪層角度對結構面內等效彈性參數(shù)的影響。結構的鋪層順序設計為[0/90//+90/0/90],其中變量表示纖維增強阻尼薄膜的鋪層角度,即保持上、下蒙皮鋪層角度不變,改變阻尼薄膜的鋪層角度,得到的變化率曲線如圖16所示。

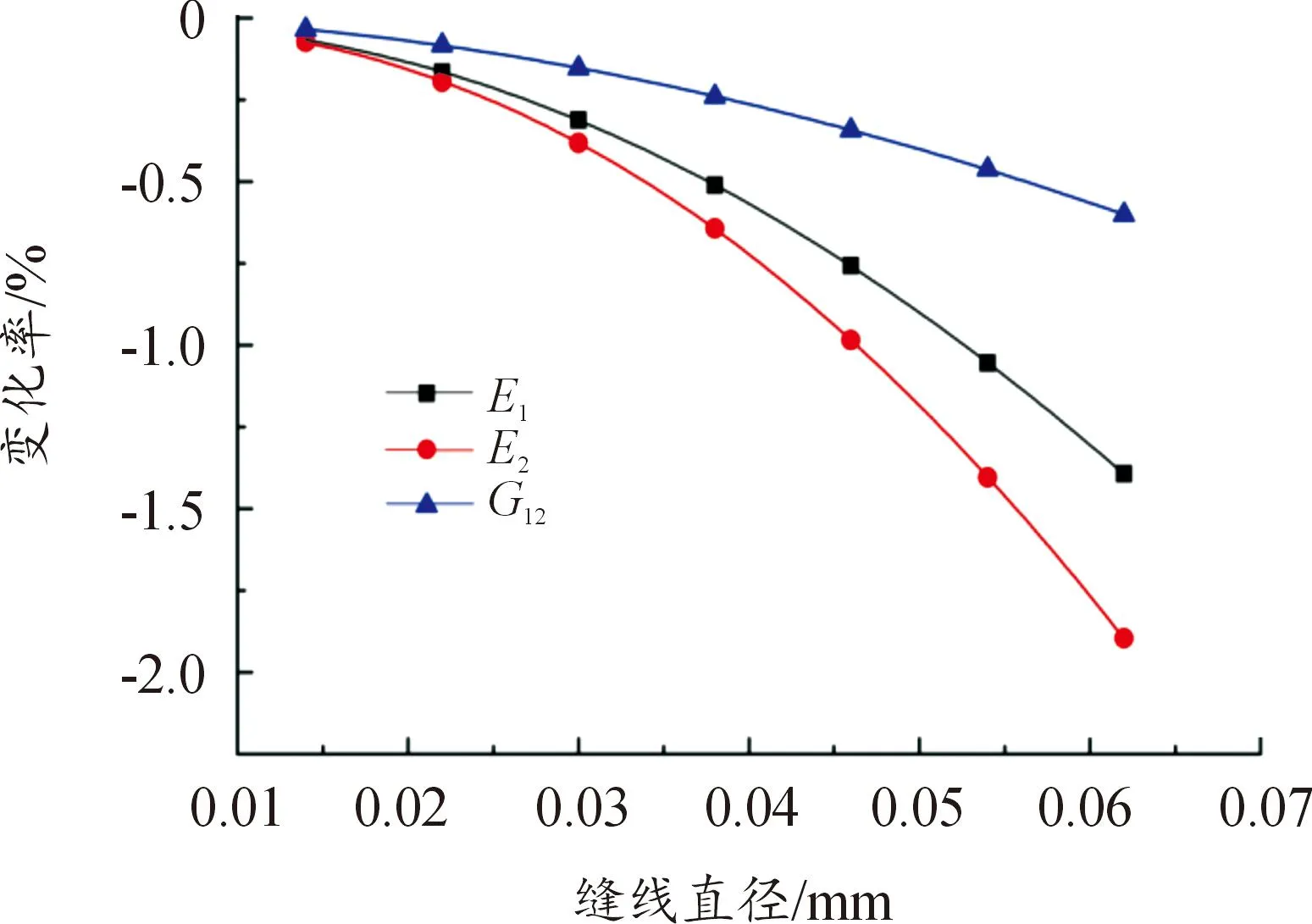
圖15 面內等效彈性參數(shù)與縫線直徑的變化關系

圖16 面內等效彈性參數(shù)與鋪層角度的變化關系

由圖16可知:與鋪層順序為[0/90/0/90/0/90]的ECSDC 相比,鋪層角度對結構面內等效彈性參數(shù)的影響比較明顯。隨著纖維增強阻尼薄膜鋪層角度的變化,ECSDC 的彈性模量和剪切模量均呈現(xiàn)出周期為π/2的正弦曲線變化。當鋪層角度是45°的奇數(shù)倍時,結構的等效剪切模量G12達到最大值。

4 結論

本研究中建立了復合釘貫通的面內纖維折線變形模型,推導了嵌入式共固化縫合阻尼復合材料面內等效彈性參數(shù)的數(shù)學表達式,并通過ANSYS 有限元數(shù)值模擬和文獻對比驗證了該理論模型的準確性,進一步研究了縫合密度、縫線直徑和鋪層角度對 ECSDC 結構面內等效彈性參數(shù)的影響,為該結構的動力學與幾何非線性研究奠定基礎。主要結論表明:

1) 由于富樹脂區(qū)、面內纖維偏轉和纖維損傷等因素的影響,縫合后的 ECSDC 結構較縫合前復合材料的面內等效彈性參數(shù)有所降低,但結構的各向異性得到了增強;

2) 當縫線直徑和鋪層角度不變,ECSDC 結構的面內等效彈性參數(shù)會隨縫合密度的增大而降低;

3) 當縫合針距、縫線行距和鋪層角度不變,ECSDC 結構的彈性模量和剪切模量隨縫線直徑的增大而降低;

4) 當各縫合參數(shù)和蒙皮鋪層角度不變,隨著纖維增強阻尼薄膜鋪層角度的變化,ECSDC 的彈性模量和剪切模量均呈現(xiàn)出周期為π/2的正弦曲線變化。當鋪層角度是45°的奇數(shù)倍時,結構的等效剪切模量G12達到最大值。