面向不均衡數據的重采樣算法

朱 深,徐 華,成金海

(江南大學 人工智能與計算機學院,江蘇 無錫 214122)

1 引 言

分類學習是機器學習的重要研究方向之一,傳統的分類模型,比如決策樹、神經網絡、SVM等,在解決分類問題時,假設樣本分布在本質上是平衡的,但是在實際問題上,為了更高的精確率,算法更容易傾向于識別多數類,少數類容易被誤分,但更多的情況,識別少數類是更重要的.

針對不平衡問題,已有的解決方法主要分為兩類:數據層面和算法層面.算法層面的方法有代價敏感學習和集成學習等.代價敏感學習的基本思想是對于不同類型的數據設置不同的誤分類代價.集成學習通過構建并結合多個分類器來完成學習任務,Sun等[1]將Boosting集成和代價敏感因子[2-4]結合,AdaBoost(Adaboost Algorithm Based on Cost Sensitivity,AdaCost)集成算法由此被提出,Krawczyk等[5]結合代價敏感與Bagging集成,在基決策樹中引入代價敏感因子.平瑞等[6]提出了基于聚類的弱平衡代價敏感隨機森林算法(Weak Balance Cost-Sensitive Random Forest,WBC-RF),該算法通過對大類樣本聚類后,隨機選擇每個聚類中的部分樣本,進行欠采樣,使用欠采樣后的數據集訓練代價敏感決策樹,但是需要生成的聚類個數過多,導致時間復雜度變高.

數據層面一般采用過采樣或欠采樣來改變數據分布Chawla等[7]提出了合成少數類過抽樣技術SMOTE算法,使用部分少數類合成新的樣本點,但是合成的樣本可能落在多數類的區間中,使多數類和少數類更難以區分.對此研究者對其做出了很多改進.Borderline-SMOTE[8]通過鄰域樣本數量區分邊界與非邊界區域,合成邊界樣本,但在某些情況下,邊界樣本難以被識別.趙清華等[9]提出了最遠點算法(Max Distance SMOTE,MDSMOTE),只關注少數類樣本質心點和距離質心點最遠距離的樣本點,但這樣會有較高的時間復雜度.劉金平等[10]提出了融合譜聚類的自適應總和采樣算法(SCF-ADASYN),但當樣本數目較大時,效果不佳.

欠采樣算法是僅選擇數據集中部分的多數類樣本.使用安全篩選[11,12]規則可以找到數據集中對分類決策沒有作用的樣本,石洪波等[13]提出了基于安全樣本篩選的欠采樣和SMOTE結合的抽樣方法(Screening_SMOTE),既減少多數中的噪聲樣本,也減少了過抽樣帶來的過擬合問題.Rayhan等[14]提出抽樣算法(Clustering based Under-Sampling approach with BOOSTing algorithm,CUSBOOST),該算法首先生成聚類,然后在每個聚類中隨機選擇部分樣本;Lin等[15]種基于聚類的欠抽樣方法,簡稱UC,生成和少數類樣本同樣多的聚類,然后將簇芯作為多數類樣本,但當少數類樣本較多時,需要產生的聚類個數過多,造成較大的系統開銷,并且會加重噪聲點對分類產生的影響.基于樣本加權的欠抽樣方法[16,17]通過多次聚類確定實例的權重,然后依據樣本的權重對多數類數據進行欠抽樣,但是這樣時間復雜度會過高.魏力等[18]提出了CBNM(Clustering-Based NearMiss)算法,根據簇芯到樣本的距離賦予該樣本的選擇權重.熊炫睿等[19]提出了一種基于簇內樣本平均分類錯誤率的混合采樣算法(SABER),該算法首先使用SMOTE算法過采樣,隨后使用聚類算法,根據簇內樣本分類錯誤率進行欠采樣.以上幾種方法,在篩選過程中耗費了較多的系統資源,應進一步改進.

為了更進一步提高SMOTE算法的性能,Bastista等[20]提出了將SMOTE算法和數據清洗方法相結合的方法SMOTE+ENN(Edited Nearest Neighbor)和SMOTE+Tomek links.董明等[21]結合SMOTE和局部核心的過抽樣算法LCSMOTE,該方法先使用自然近鄰除去噪聲,隨后劃分區域,計算區域內樣本的稀疏權重,最后合成新樣本.梅大成等[22]提出了一種征邊界和密度適應的SMOTE算法,該算法找出每一個少數類樣本的邊界范圍,同時根據樣本的分布密度時刻改變算法參數.以上兩種算法步驟較復雜,并且時間復雜度較高,可以進一步提升.崔鑫等[23]提出SMOTE的改進算法CSMOTE(Clustered Synthetic Minority Over-sampling TEchnique).該算法使用少數類的簇心,與對應簇中被篩選后的樣本合成樣本,一定程度上減少了噪聲數據的干預,但是在面對大數據集,類別不平衡比較嚴重的時候,要合成的樣本較多,篩選機制又較苛刻,會造成較大的系統開銷.針對于該算法的缺點,本文基于此提出了一種SMOTE的改進算法,該算法先使用聚類算法將少數類分為若干個簇,從簇中隨機選擇若干個樣本點,使用線性插值法合成一個中間樣本點,再使用合成的中間樣本點與聚類簇芯合成一個新的樣本點,并將其添加到數據集中,使用簇內的樣本在一定程度上減少了噪聲數據的干擾.

本文將SMOTE的改進算法與隨機欠采樣RUS算法結合,提出了一種重采樣算法RUSCSMOTE(Random Under-Sampling Clustered Synthetic Minority Over-sampling TEchnique),該算法先自適應的通過欠采樣去掉部分多數類樣本,這樣既保留了部分多數類的信息,又減少了合成的少數類,因此也減少了系統開銷和噪聲點的干擾,同時降低了算法時間復雜度,再利用SMOTE的改進算法過采樣,減少了新合成的樣本落在多數類的樣本空間中的概率,最終得到均衡的數據集.

1 RUCSMOTE算法

1.1 隨機欠采樣算法

隨機欠采樣即從多數類Smaj中隨機選擇一部分樣本,組成樣本集Sr.然后將Sr從Smaj中移除,原數據集如圖1(a)所示,經過欠采樣之后,數據分布如圖1(b)所示,多數類樣本點變少,使得樣本均衡分布.

圖1 隨機欠采樣Fig.1 Random under-sampling

算法缺點:對于隨機欠采樣,丟棄了一部分樣本,因此會造成信息缺失,這意味著刪除多數類樣本有可能會丟失部分有用的信息.算法優點:算法簡單易實驗,減少模型訓練的時間.

1.2 SMOTE改進算法思想

SMOTE算法如圖2(a)所示,先隨機選出一個少數類樣本c,然后找出該樣本的k個近鄰(假設k=4),然后從k個近鄰中隨機的選擇一個樣本d,在該少數類樣本c和被選中的d這個少數類樣本之間的連線上隨機找一點e,這就是合成的樣本點.顯然樣本e出現在多數類的空間中,這種情況下非但不能幫助分類器的訓練,反而會因為樣本e讓數據變得更難區分,因此要采取一些措施保證合成樣本的合理性.

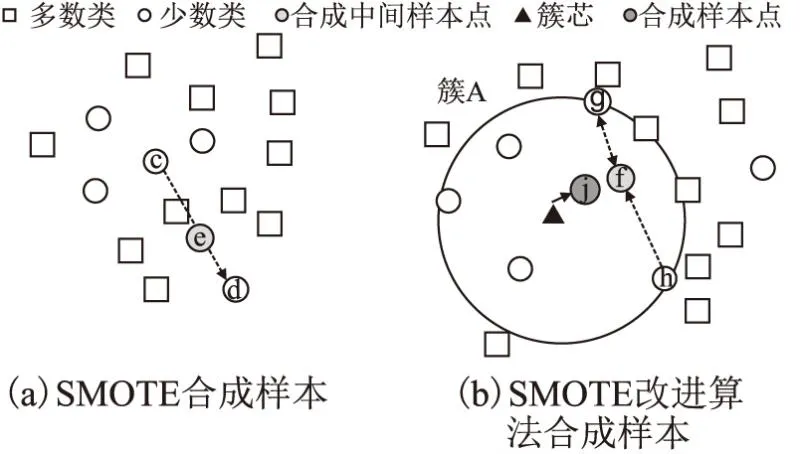
圖2 SMOTE和SMOTE改進算法合成樣本對比Fig.2 Comparison of synthetic samples of smote and improved smote algorithms

SMOTE改進算法首先在少數類上使用聚類算法,將少數類分為若干個簇,在各個簇中合成新樣本.如圖2(b)所示,首先在少數類上生成若干個簇,然后分別在各自簇中合成新的樣本,以簇A舉例,算法過程為:隨機選擇若干少數類樣本,比如隨機選擇兩個樣本點,g點和h點,使用線性插值法,在兩個點連線部分隨機生成一個點f,然后使用新合成的少數類中間樣本與聚類中心合成新樣本j,最后將j加入到少數類樣本集中.

該算法使用聚類算法,在簇中合成新樣本,減少了新合成的樣本位于多數類的樣本空間中.由于參與合成的少數類聚類的簇芯,部分樣本合成中間樣本點,都不是原數據集中實際的數據點,增大了樣本的分布,減少了過擬合的風險.

1.3 k-means聚類算法

給定樣本集D={x1,x2,…,xn},該算法針對聚類所得簇劃分C={C1,C2,…,Ck}最小化平方誤差:

(1)

輸入:樣本集合D,聚類簇數k

1)從D中隨機選擇k個樣本作為初始聚類中心;

2)計算樣本集合中其他樣本到聚類中心點的歐式距離,將樣本分配到距離最近的聚類中心點所在的簇中;

3)根據已經劃分好的簇,更新聚類中心點;

4)重復2)和3)的過程,直到中心點不再移動;

輸出:簇劃分C={C1,C2,…,Ck}

1.4 RUCSMOTE算法流程

RUCSMOTE算法是將隨機欠采樣算法和SMOTE的改進算法結合起來,簡要步驟為:

1)自適應的對數據集使用隨機欠采樣,減少多數類樣本數量;

2)將樣本分為多數類和少數類;

3)在少數類上進行聚類,生成k個簇;

4)將所有的簇芯加入到合成的少數類集合中;

5)使用簇內的樣本合成中間樣本點,然后與各自的簇芯合成新的少數類;

6)將新合成的樣本與原數據集合并,得到均衡的樣本集.

rate表示多數類樣本數量和少數類樣本數量的比值,即不平衡比率,rate1表示欠采樣后的不平衡比率.使用一個0～1之間的隨機數R,點xi和xj合成新樣本xnew的公式如下:

xnew=μi+R(xj-μi)

(2)

RUCSMOTE算法的具體步驟如下;

輸入：不均衡數據集S={x1,x2,…,xn},聚類個數k,不平衡比率rate

過程：

1. 根據rate的數值,設置參數rate1控制欠采樣比率,

2. 使用隨機欠采樣后,得到數據集S1;

3. 根據類別,將S1分成兩個集合,分別是多數類集合

4.Smax和少數類集合Smin;

5. 令合成的少數類集合NewM=φ

6. 在集合Smin上使用k-means算法進行聚類生成k個

7. 簇C={C1,C2,…,Ck},求出各自的聚類中心

8. {μ1,μ2,…,μk},將聚類中心加到NewM中;

9.fori= 1,2,…,kdo

10. 依次遍歷集合C,取集合中的Ci;隨機選擇兩個樣

11. 本點,使用公式2)合成中間點xtemp,利用簇Ci

12. 的簇芯ui和xtemp合成樣本xnew,將xnew加入

13. 到NewM中;

14.endif

輸出：將NewM與原樣本集合并,合成均衡樣本集NewS

1.5 RUCSMOTE算法復雜度分析

少數類樣本數量用n表示,多數類樣本數量用m表示,樣本的維度為p.步驟1對多數類進行隨機欠采樣,時間復雜度為O(m),步驟2的時間復雜度為O(m+n),步驟3對少數類使用k-means聚類算法,算法時間復雜度為O(fpkn),其中f為迭代次數,k是類別數,因為一般情況下f,p,k遠小于n,所以k-means算法時間復雜度簡化為O(n).步驟4～步驟5中,假設簇是被等分的,則時間復雜度為O(m),綜上RUCSMOTE的時間復雜度為O(m+n).

其相對于許多重采樣算法,該算法的時間復雜度是較低的.因為引進了隨機欠采樣的步驟,不僅需要合成的樣本減少,減低時間復雜度,同時減少了噪聲點的干擾,減少過擬合風險.

2 實驗結果與分析

2.1 實驗數據集和評價指標

KEEL數據庫是(KEEL:A software tool to assess evolutionary algorithms for Data Mining problems(regression,classification,clustering,pattern mining and so on))不平衡數據集,里面的很多數據集來源于現實生活中,本文算法適用于數值型數據,從KEEL數據庫中選取20個不平衡數據集,數據集的詳細信息見表1,為了方便表示,給每個數據集取標號.

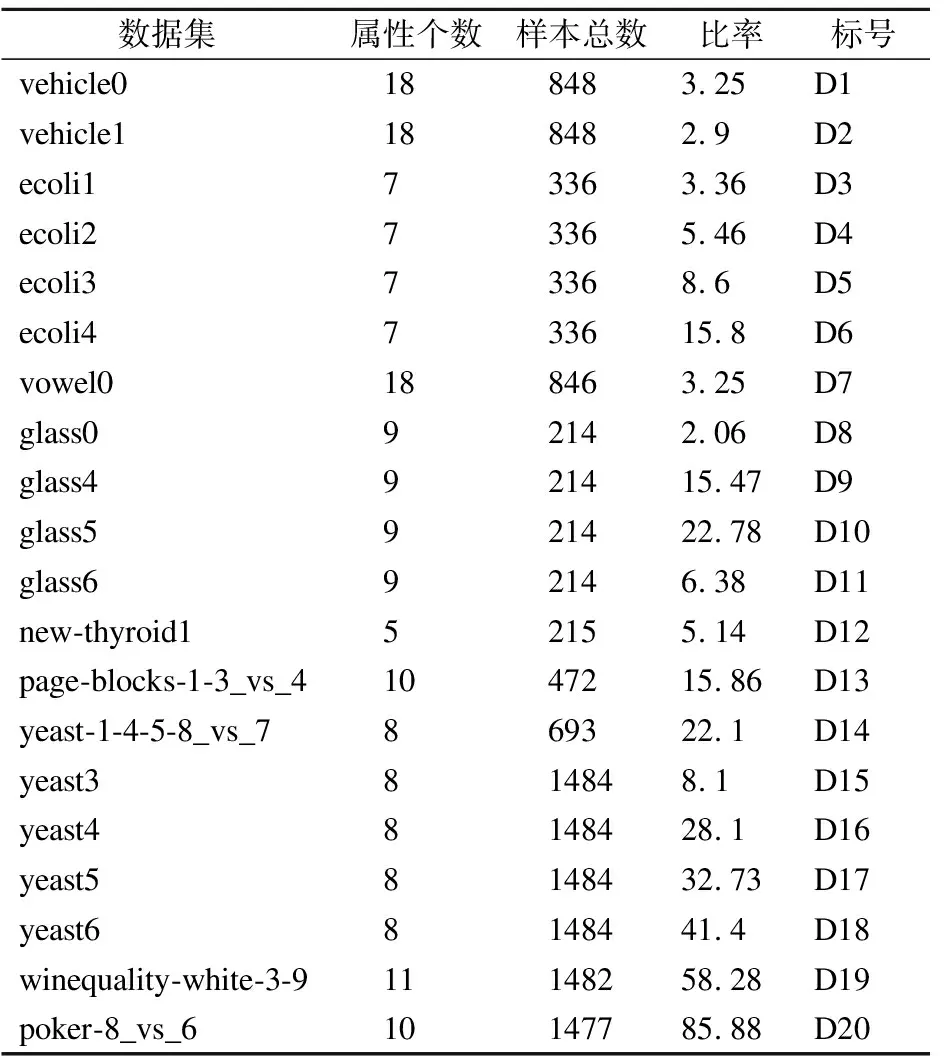
表1 數據集詳細信息Table 1 Details of datasets

常用的分類準確率更偏向于多數類數據,因此不適合作為不平衡數據的性能度量.可以將根據樣本的真實類別和分類器預測的類別的組合建立混淆矩陣,其中TP表示真正例的數量、FP表示假正例的數量、TN表示真反例的數量、FN表示假反例的數量,本文采用受試者工作特征曲線(Receiver Operating Characteristic,ROC)的面積,即AUC(Area Under ROC Curve)以及G-means來比較分類器的性能.

AUC是不平衡問題分類性能的通用度量方式,AUC的取值范圍為[0,1],AUC的數值越大,其分類泛化性能越好,最理想狀態下數值為1,而AUC為0.5時,效果等同于隨機猜測.TPR表示“真正例率”,FPR表示“假正例率”,Specificity為多數類數據的預測準確率,三者定義如下:

(3)

(4)

(5)

AUC計算式如下:

(6)

G-mean通過計算多數類和少數類數據的預測準確率的幾何平均值,只有其分類泛化性能越好的時候,才能得到較高的G-mean值,G-mean簡記為GM,GM值的計算公式如下:

(7)

2.2 實驗步驟

在進行最終實驗之前,先做3個小實驗確定算法參數,設置不同參數,選取7個數據集,對數據集進行5次五折交叉驗證,求出分類器的GM值和AUC值的平均值,記錄在表中,其中不同參數下第1行為AUC值,第2行為GM值,每種數據集上較優的算法已加粗顯示.

最后對使用RUCSMOTE算法與另外7種經典的重采樣算法,在20個數據集上,進行5次五折交叉驗證,求出分類器的GM值和AUC值的平均值,對比不同算法的表現,為了更好體現該算法的性能,分類器使用單層決策樹,本文對數據集進行標準化處理,減少不同變量的取值范圍對算法的影響.

2.3 算法參數設置

算法有3個重要的參數,分別是少數類產生的聚類個數,參與合成新樣本點的樣本點個數,以及多數類的欠采樣率,3個參數關聯性不大,所以分開確定.

首先確定參與合成新樣本的樣本點,由理論分析可知,當只選擇一個樣本點與簇芯合成的時候,由于使用了一個真實的樣本點,在合成的過程中可能會使得新合成的樣本點與真實存在的樣本點距離過近,容易導致過擬合,如果先隨機選擇兩個樣本點合成中間樣本點xtemp,然后使用xtemp與簇芯合成新的樣本點,由于兩個點都不是真實的樣本點,并且合成的點偏向聚類內部,所以可以更好的增加樣本的分布.

如果使用3個或者3個以上的樣本點合成,由于本就已經隨機選擇的兩個點,再增加隨機樣本點可能會導致新合成的點偏離原本的分布,所以通過理論分析可知,選擇隨機選擇兩個數據點較為合適.

下面通過實驗驗證,設聚類個數k=5,先不使用隨機欠采樣,在選取的數據集上測試,結果如表2所示.

表2 隨機點個數對算法性能影響Table 2 Influence of the number of random points on the performance of the algorithm

從試驗結果來看,只有D19的GM值在樣本點為3時超過了樣本點為2的,其他數據集在選取兩個數據點的效果是更好的,隨著選取的樣本點變多,分類效果反而變差,這也與理論分析一致.

聚類個數k會影響合成少數類的分布情況,在一些少數類樣本較少的情況下,k過大可能會超過樣本總數,并且隨著聚類個數增多,噪聲點對于分類器的影響也會變大,時間復雜度也較高,所以k不宜取的過大,但是選取的k過小會增加合成新樣本落入多數類空間的概率,反而影響分類結果,所以參數k的選取對算法性能很重要.

取k∈{2,3,4,5,6,7},通過對比不同k下分類器所得的AUC值和GM值來確定最佳的k值,選取7個數據集進行測試,結果如表3所示.

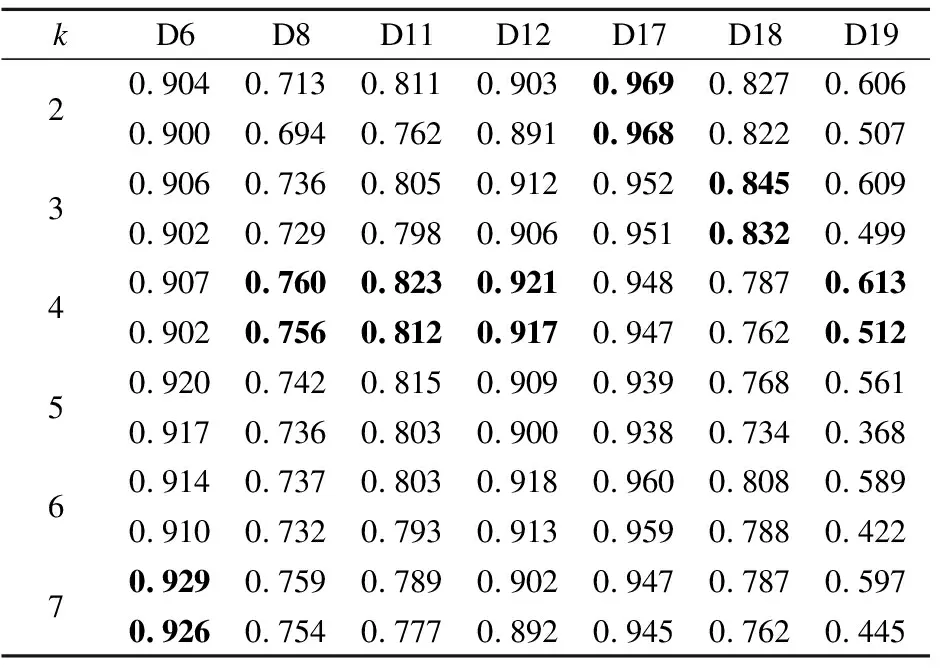
表3 不同k值的分類效果Table 3 Classification effect of different k values

表3中有4個數據集在k=4時取得了最優值,D17和D18分別在2和3時取得最優值,由于每種數據結的樣本分布不同,k無法完全統一,但是聚類個數在4左右時,總能取得較好的結果,并且時間復雜度較低,受噪聲影響也較小,因此默認情況下聚類個數k=4.

該算法還需要平衡過采樣和欠采樣,在實驗中,嘗試將rate等比例縮放或非線性的縮放,降低到rate1,對比兩者的效果.等比例縮放是將不平衡比率rate降低到多數類和少數類差值的1/s倍,當s過于大時,近乎于只有欠采樣,所以s不宜過大,取s∈{2,3,4,5},此時:

(8)

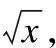
rate1=log2(rate+1)

(9)

(10)

在數據集上使用不同的rate1公式的重采樣算法,如表4所示,可以看出,當不平衡比率較低時,非線性縮放的效果一般,但是隨著不平衡比率的上升,非線性縮放普遍優于等比例縮放,其中公式(10)的效果更好,而且在面對大數據集,不平衡比率較高的情況下,可以減少更多需要合成的樣本,因此使用公式(10)來確定欠采樣的比率.

表4 不同欠采樣公式的算法分類性能對比Table 4 Comparison of algorithm classification performance of different under sampling formulas

2.4 不同算法的性能比較

本文選取9種重采樣算法對原始數據集進行抽樣,然后與RUCSMOTE算法對比抽樣數據集上構建的分類器的性能.它們分別是SMOTE[7]、MDSMOTE[9]、WBC-RF[6]、Borderline-SMOTE[8]簡記為BLSMOTE、CSMOTE[23]、隨機欠抽樣RUS、SMOTE+ENN[20]、SMOTE+TomekLink以及文獻[15]提到的基于聚類中心的欠采樣,簡稱UC.對每個數據集分別使用這10種算法進行5次五折交叉驗證,求出其AUC和GM的平均值,如表5所示,其中每個數據集的第1行為AUC值,第2行為GM值.

表5 不同數據集上8種算法分類性能對比Table 5 Classification performance comparison of eight algorithms on different datasets

由表5可知,RUCSMOTE算法在D2～D6由于樣本數較少,并且不平衡比率較低,沒有進行充分的欠采樣和過采樣,相對于其他算法優勢不大,因此沒有取得最佳的效果,但是和最優的是比較接近的,在后續不平衡比率較高的數據集上,性能更優.作為改進的SMOTE算法,對比SMOTE,AUC和GM均有提升,在D9,D10,D18,D19上的提升尤為明顯,在不平衡比率較高的D19上AUC提升了13%,在GM上提升了40%,因為通過聚類選擇的點相當于進行了篩選,更合理的擴充了數據集的分布,同時降低合成的數據點落入多數類樣本的區間,降低了過擬合的風險與單純的欠采樣相比,由于保留了更多的多數類,模型可以學習到更多的多數類信息,除了在D14上,在其余的數據集上均優于單純的欠采樣算法,這是因為在一些少數類與多數類樣本空間相互重疊較為嚴重的數據集,多使用欠采樣更有利于二者的區分.求出不同算法在數據集上AUC和GM的平均值,可以看到RUCSMOTE算法的平均值最高,在AUC上超過SMOTE算法4.19%,超過隨機欠采樣2.89%,在GM上超過SMOTE算法7.68%,超過隨機欠采樣2.56%,這表明RUCSMOTE算法是可靠的.

3 結 語

本文從數據層面出發提出了RUCSMOTE算法,實現了不平衡數據再平衡,該算法先使用簡單高效的隨機欠采樣丟棄一部分多數類,緩解一般欠抽樣丟失樣本過多導致的信息丟失問題,然后使用聚類算法分類,使用簇芯在聚類內合成新樣本,解決了SMOTE算法模糊多數類和少數類的邊界問題,同時使得擴充了樣本的分布,使得新合成的樣本更合理又因為使用欠采樣使得需要合成的樣本數減少,降低了過擬合的風險.在實際的實驗中也證明了,尤其是在不平衡比率更高的時候,該算法有較好的分類效果,并且算法易于實現,時間復雜度更低,但是在樣本數較少并且不平衡比率較低時,算法優勢并不明顯,這也是未來要進一步優化的方向之一.