基于多傳感器數據融合的機房火災檢測算法

張 冉，吳云韜*，于寶成，徐文霞

1. 智能機器人湖北省重點實驗室（武漢工程大學），湖北 武漢 430205；

2. 武漢工程大學計算機科學與工程學院，湖北 武漢 430205

機房作為數據中心，各領域對其環境穩定性的要求日益提高，若不及時處理由設備故障引起的火災，將會導致火勢變大，給機房帶來巨大損失，為此，在火災發生初期進行準確識別并給出相應警報預警，對無人值守機房的安全維護尤為重要。在火災發生初期，周圍環境中的氣體、溫度都會發生相應變化，并且參數相互關聯，機房傳統的檢測通過單一參量變化無法確定火災是否發生，情況復雜時，易發生誤報、漏報情況。因此，學者們的研究熱點逐漸集中于基于多傳感器的火災檢測。鄭皓天等［1］通過遺傳算法對誤差逆傳播（back propagation，BP）神經網絡進行優化，提出了基于3 種不同特征參量的火災識別算法。蘇醒等［2］利用復合數字濾波法以及模糊推理技術，并結合多傳感器數據融合技術，實現了對火災的預測。Zervas 等［3］通過多傳感器數據融合技術研究火災早期情況，并通過參考溫度、濕度和視覺傳感器覆蓋的區域等特征，結合Dempster/Shafer（D-S）證據理論推斷火災發生可能性。Liang 等［4］通過BP 神經網絡對溫度、CO 濃度、煙霧濃度進行融合，實現了火災的早期預警。

上述火災探測方法不同，因此適應的對象和范圍也有差異，人工神經網絡（如BP 神經網絡）具有自適應性等優點，但需要較大的訓練樣本，訓練時間比較長［5］。 支持向量機（support vector machine，SVM）對解決小樣本有著特殊優勢，算法較簡單，但需要設置大量參數，不合理的參數設置會使算法性能變得很糟糕［6］，且參數的設置對算法的精確度有較大影響［7］。由于極限學習機（extreme learning machine，ELM）泛化能力強，且學習速率快［8］，為此針對機房火災檢測，本文采用麻雀搜索算法（sparrow search algorithm，SSA）優化ELM 并結合模糊推理的數據融合算法，將環境特征（如溫度、煙霧濃度、CO 濃度）與火災持續時間、設備保護等級等信息進行數據融合，最終決策出火災警報等級，實現對機房火災探測與維護。

1 多傳感器數據融合原理及設計

為實現對火災更準確、快速地探測，本文采用多傳感器數據融合技術，結合環境特征及其他特征參數進行綜合決策，火災探測融合算法結構主要流程為：通過對火災現場中傳感器采集到的信息數據進行特征融合，并結合火災現場的其他參數信息進行決策層綜合分析，最終得到可以判斷火災是否發生的預警信息。

信息層選用3 種傳感器（CO 傳感器、溫度傳感器、煙霧傳感器）完成對火災的探測，并對信息進行預處理，特征層對特征參量進行特征數據提取，并對提取的數據進行特征融合，分析出火災發生概率，決策層將火災發生概率與火災現場的其他多特征參數信息進行融合判斷分析，其中多特征參數信息包括火災延續時間、不同氣候（溫度和濕度等環境影響）影響下的各類不同設備保護等級，最終決策出火災是否發生。

2 多傳感器數據融合火災檢測算法

2.1 信息層實現

本文采用多種傳感器對環境信息進行收集，用來判斷火災的發生，由于不同類型的傳感器收集信息的特征參量范圍、大小都不相同，需進行歸一化處理，歸一化公式見式（1）。

對于式（1），c表示傳感器采集CO 濃度、煙霧濃度、溫度等數據的參量個數，Ac表示輸入c個參量后歸一化后的值，Xc表示由實驗數據確定的c個參量的輸入值，Xmin和Xmax分別為選取參量的最小輸入值和最大輸入值。

2.2 特征層數據融合處理

2.2.1 極限學習機 ELM 是由高瀅等［9］提出的一種新型神經網絡算法，ELM 與傳統神經網絡相比，具有參數設置更少、學習效率更高、泛化能力更強等優點。ELM 的網絡結構由輸入層、隱含層、輸出層3 部分組成，是一種新式的前饋神經網絡，通過對隱含層神經元數目進行設定，利用解方程的方法得到輸出權值。ELM 網絡結構如圖1 所示。圖1 中X1~X3為輸入神經元節點；Wij為第i個神經元與隱含層神經元j之間的連接權值；bjk為隱含層神經元j與輸出層第k個神經元之間的連接權值；Y1~Y3為模型輸出。

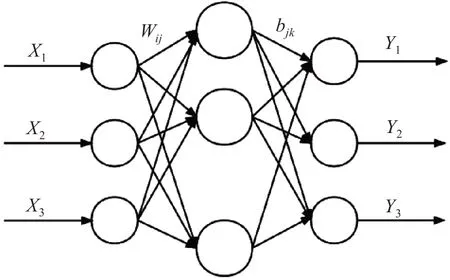
圖1 ELM 網絡結構Fig.1 ELM network structure

本次ELM 網絡結構模型中，X、Y分別為輸入值和輸出值，其數學模型如式（1-3）所示。

式中：w為輸入層和隱含層之間的連接權值矩陣，l為隱含層中的神經元數目，n為輸入層神經元數，wln為輸入層和隱含層之間的l層n列的連接權值。

式中：b為隱含層和輸出層之間的連接權值矩陣，m為輸出層神經元數，blm為隱含層和輸出層之間的l層m列的連接權值。

式中：a為隱含層神經元閾值矩陣，其中al表示隱含層中第l個神經元的閾值。

ELM 網絡輸出模型為：

式中：T為輸出數據集，tm表示第m個訓練樣本的網絡輸出值，tj為矩陣T的列向量集合，tmj表示第m個輸出神經元對應于隱含層神經元j的輸出值，bim表示隱含層神經元j對輸出神經元m的連接權值，g(?)為隱含層神經元激勵函數，xj為隱含層神經元j的輸入樣本，wi為隱含層神經元j對應輸入樣本xj的權值，ai為隱含層神經元j的閾值。

可將式（4）簡寫為T′=Hb，其中T′為T的轉置矩陣，H為隱含層輸出矩陣，H的表達式為：

式中：wl表示隱含層第l個神經元的權值，xQ表示輸入的第Q個數據樣本。

2.2.2 麻雀搜索算法 麻雀搜索算法［10］是一種新型的群智能優化算法，主要受麻雀的覓食和反哺食等行為的啟發，具有尋優性強、收斂速度快等特點，SSA 算法中，麻雀種群被分為發現者和加入者，麻雀搜索算法首先需對麻雀種群與適應度進行初始化，種群采用隨機生成位置的方法初始化麻雀種群的個體位置，數學表達式如式（6）所示。

式中：s為麻雀數量，d為要優化的變量維度，xsd表示第s個麻雀對于第d個參數的取值，具有較好適應度值的麻雀在覓食過程中，需對食物進行迭代搜索，其位置變化采用式（7）更新：

式中：t為當前迭代的次數；Xt,qr和X(t+1),qr分別表示第t次和第t+1 次迭代中，具有較好適應度值的第q只麻雀在維度r上的位置；tmax為本次計算中最大的迭代次數；R2為預警值，R2∈［0，1］；F為安全值，F∈［0.5，1］；Q為隨機數，服從正態分布；a表示隨機數，a∈（0，1）；L為一個1×d的矩陣，其中所有元素值都為1；q=1，2，3，… ，s；r=1，2，3，…，d。

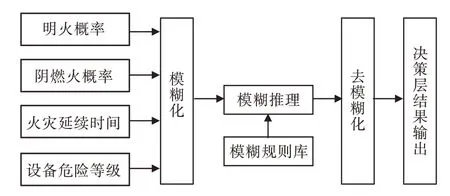
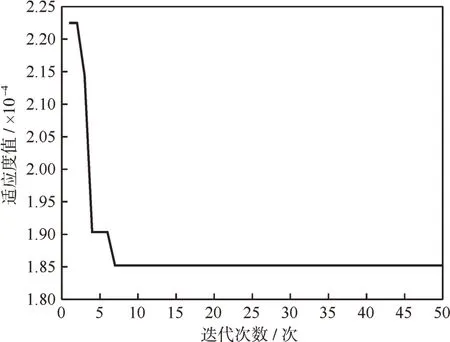
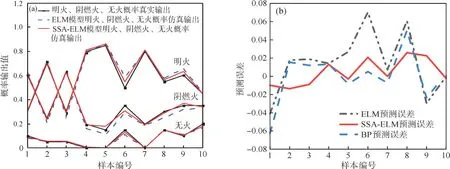
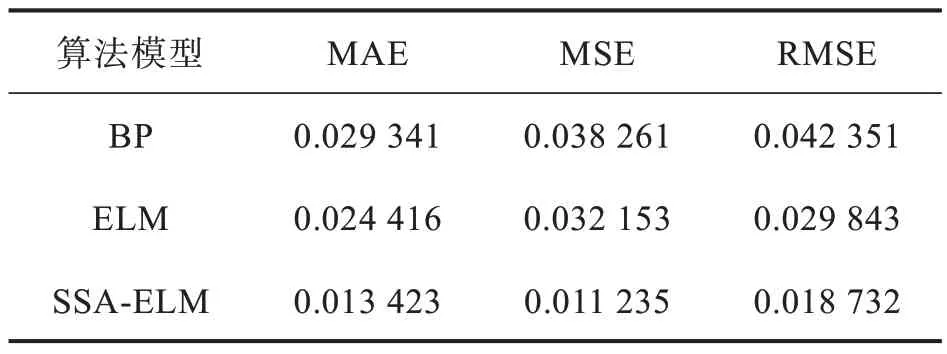
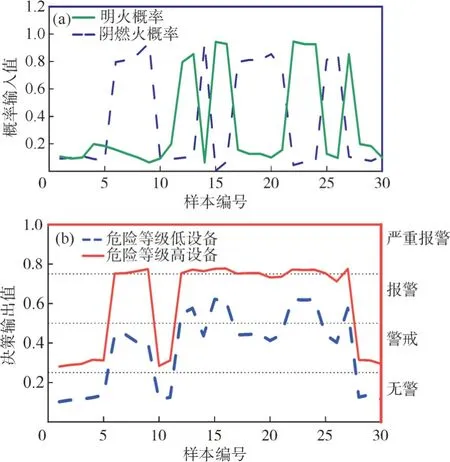
當R2

式中：X(t+1),p為第t+1 次迭代后發現者的最優位置，Xt,w為第t次迭代全局最差位置，A為1×d矩陣，每個元素隨機選取1 或-1，A+=AT(AAT)-1，當q>s/2，說明適應度較低的第q個加入者未得到食物，需飛往其他地方覓食。

一般情況，假設這些意識到危險的麻雀占總數量的10%到20%，它們的初始位置在種群中隨機產生，其數學模型如式（9）所示：

式中：Xt,b為第t次迭代后全局最優位置；B為步長控制參數，是一個服從均值0，方差1 的正態分布的隨機數；K為隨機數，K∈［-1，1］；ε為常數；fq為麻雀個體的適應度值；fg和fw分別為全局最好和最差適應度值。

當fq>fg，表明該麻雀處于全局危險位置，大概率受到攻擊；當fq=fg，表明該麻雀意識到自身大概率被捕食的危險，需盡快移動并與種群匯合。

2.2.3 基于SSA-ELM 特征層數據融合模型 算法模型步驟如下：

（1）數據進行歸一化，并分配訓練集和數據集。

（2）對麻雀優化算法的迭代次數、種群、發現者以及加入者比例進行初始化。

（3）構建極限學習機網絡結構，設置網絡參數。

（4）計算麻雀群體的適應度值，并找到最佳適應度值fg和最差適應度值fw。

（5）根據式（7-9）更新發現者、加入者及意識到危險麻雀的位置，若更新后的位置優于先前的，則替換它。

（6）進行迭代，不斷更新麻雀位置，達到tmax時停止，迭代過程中適應度最低的麻雀為最優解。

（7）迭代完成，將得到的最優權值和閾值賦予極限學習機，構建SSA-ELM 模型。

2.3 決策層數據融合模型

2.3.1 決策層模型構建 決策層主要對各決策因子之間的關系進行分析，并輸出分析結果。為更好判斷火災發生概率對火災是否發生的影響，在決策層采用模糊推理技術［11］進行融合，本文引入4 種決策因子（明火概率、陰燃火概率、火災延續時間、設備危險等級）。

火災延續時間T由式（10）判定。

式中，h表示當前時間段，h+1 表示下一個時間段，Yi(x)表示從特征層輸出的明火、陰燃火概率，V（·）為階躍函數，Td為將要報警的閾值。

本文對機房火災進行預測，由不同設備所處的周圍環境決定其危險等級，比如在機房門廊、過道等邊緣位置，設備危險等級可表示為低；在不間斷電源（uninterruptible power supply，UPS）、電閘等設備所處的機房核心位置，其危險等級應表示為高，面對不同位置的設備根據實際情況確定其危險等級。

決策層模型如圖2 所示，該模型通過結合各決策因子，結合模糊化處理，決策出最終結果。

圖2 決策層融合模型流程Fig.2 Decision level fusion model process

2.3.2 決策層信息融合 輸入/輸出量的模糊化：在決策層信息模糊化處理中，將輸入量（明火概率、陰燃火概率、火災延續時間、設備危險等級）進行模糊化處理，模糊集劃分為正小（PS）、正中（PM）、正大（PH），隸屬函數采用三角函數。輸出量模糊集劃分為無（PN）、小（PS）、中（PM）、大（PB），隸屬函數采用三角函數。

模糊邏輯推理：本文通過實際情況對火災進行辨識，從而建立模糊規則。根據馬達尼法推理規則推斷，模糊規則庫的數量可根據輸入量之間的關系來確定，本文在系統中有4 個輸入量，每個輸入量的模糊等級設定為3，即在模糊規則庫中建立了3×3×3×3=81 條模糊規則，其模糊規則形式為“IF（火災概率is 正小）and（火災延續時間is 正小）and（設備危險等級is 正小）then（決策結果輸出is正小）”。

去模糊化：根據模糊規則輸出的結果也是模糊的，需進行去模糊化操作。本文采用面積重心法去模糊化［12］，公式如式（11）所示。

式中，U表示去模糊化后得到的輸出值，用來進一步分析，u（z）為輸出的隸屬函數，z為模糊規則的輸出變量。

對去模糊化后得到的U進行多級別判斷，當U<0.25 時，判定為無火情；當0.25≤U<0.5 時，判定為警戒；當0.5≤U<0.75 時，判定為報警；當U≥0.75時，判定為嚴重報警。

3 火災檢測算法仿真分析

若機房發生火災，其周圍主要參數溫度、CO濃度、煙霧濃度會發生明顯變化，因此，采用標準試驗火數據進行仿真，分別對特征層、決策層進行算法仿真分析。麻雀搜索算法參數如下：麻雀規模為30，最大迭代次數為50，發現者比例占種群總數70%，意識到危險的麻雀占種群總數20%，安全閾值F為0.6。ELM 算法設置如下：隱含層個數為10，訓練次數為1 000，學習速率為0.01，激活函數為Sigmod。BP 算法參數如下：訓練次數為1 000，學習速率為0.01，最大迭代次數為50。

3.1 特征層SSA-ELM 模型仿真分析

本文從中國標準明火SH4、標準陰燃火SH1、廚房環境下標準干擾信號選取實驗數據40 組［13］，選取30 組作為訓練樣本，10 組作為測試樣本，進行仿真實驗分析。

圖3 為本算法SSA-ELM 模型的收斂過程，經過第6 次迭代后模型達到最優，可知本模型具有較高的收斂速度和精度。圖4（a）給出了各算法模型的預測結果，可知，經過SSA 算法優化的ELM 模型預測精度明顯高于ELM 模型，有著較強的泛化能力，通過SSA 算法對ELM 模型的權值和閾值進行優化，性能有較大提升，即SSA 算法有較強尋優能力。

圖3 SSA-ELM 適應度曲線Fig.3 SSA-ELM fitness curve

圖4 仿真預測結果：（a）火災概率仿真，（b）測試集預測誤差Fig.4 Simulation prediction results：（a）fire probability simulation，（b）test set prediction error

模型經過訓練，各模型誤差曲線如圖4（b）所示，可以明顯看出SSA-ELM 模型的誤差曲線較為平穩，其他模型誤差起伏較大。可見，SSA-ELM模型檢測精度較高，可以有效降低火災探測的誤差率，提高火災預測的準確率。

為進一步評價算法檢測結果的優劣性，選取平均絕對誤差（mean absolute error，MAE）、均方誤差（mean-square error，MSE）和均方根誤差（root mean square error，RMSE）作為預測評價指標，將優化后的算法重復執行30 次后，記錄相關指標如表1 所示。

表1 性能對比Tab.1 Performance comparison

經對比發現，在本文采用的MAE、MSE、RMSE 3 個指標上，SSA-ELM 算法的預測精度最高。可知，通過SSA 優化ELM 權值和閾值的火災檢測算法的預測精度更高，大大提高了火災檢測的準確率。

3.2 決策層模糊推理仿真分析

由特征層仿真分析可知，SSA-ELM 模型可準確識別火災發生的概率，決策層將多特征參數信息進行融合，更直接地給出警報決策。并且將特征層明火、陰燃火概率仿真結果與火災延續時間、設備危險等級等信息輸入決策層，通過仿真輸出報警決策結果。

決策層仿真采用30 組經特征層輸出的明火、陰燃火概率，通過決策層融合輸出，驗證決策層有效性。仿真結果如圖5 所示。

圖5 決策層仿真結果：（a）概率輸入，（b）決策輸出Fig.5 Decision layer simulation result：（a）probability input，（b）decision output

由圖5 可以看出，通過對明火、陰燃火概率的輸出，結合附加信息的決策層可以做出準確的決策輸出，對機房內不同危險等級的設備，可以做到明顯的識別，滿足對機房火災的準確預警。

4 結 論

針對傳統機房火災檢測的不足，本文采用了基于多傳感器數據融合的火災檢測算法，在特征層中提出了一種基于SSA 算法優化ELM 權值和閾值的火災探測模型，經研究發現，模型的泛化能力和檢測精度提升明顯，可有效提高火災檢測的準確率；在決策層中采用模糊推理技術，結合機房環境多特征信息，根據設備的危險程度靈活給出警報信息，分析不同的警報等級給出準確的火災識別結果，極大提高了火災檢測系統的準確性和靈活性。