凍結重塑黏土分數階蠕變本構模型分析

姚兆明,蹇膨遠,孔宏水,李 南

(1.安徽理工大學 土木建筑學院,安徽 淮南 232001; 2.礦山地下工程教育部工程研究中心,安徽 淮南 232001)

凍土強度是其最重要的力學指標之一,也是凍土工程領域最重要的研究課題之一[1]。自二十世紀二三十年代蘇聯科學家率先對凍土的各種性質進行研究,并逐步建立起凍土的強度理論和蠕變理論。研究發現,土體在負溫條件下的強度值遠大于自然狀態下的強度值,且土體所處的環境溫度越低,抗壓強度越大。主要原因是土體中未凍水隨著溫度的降低凍結成冰,使土體本身內部的冰含量增加,冰的強度遠大于水的強度,且冰的膠結作用增強了土壤顆粒之間的摩擦力和黏聚力,進而使凍土的強度提高[2-3]。學者開展了大量的室內外凍土強度組成性質試驗研究,Goughnour等[4]研究發現,多數情況下凍土強度大于其自然狀態下的強度與冰的強度之和,土體干重度的增大也會增大凍土強度。Ting等[5]對負溫環境下的砂土開展單軸壓縮試驗,從土壤顆粒強度、冰的強度及結構三方面分析凍土的影響機理與強度組成。凍土的蠕變特性是凍土在施加恒定加載應力后,應變隨著時間的變化增大,直至土體本身失去穩定最終達到破壞的過程[6]。學者通過構建諸多蠕變模型來模擬凍土的蠕變行為,可分為經驗模型、流變模型和黏彈塑性模型等三類。曹虎生等[7]在開爾文模型的基礎上進行改進,并對優化后的參數與溫度線性回歸,得到了考慮溫度的凍土蠕變模型。姚兆明等[8]建立了考慮溫度效應的凍結黏土內變量蠕變模型,利用智能算法對模型參數進行計算和修正,并用不同加載等級的蠕變試驗對模型進行驗證,結果表明該模型可較好地模擬凍土蠕變行為。

上述模型均為整數階蠕變模型,其對于巖土蠕變中介于理想固體與理想液體之間的力學性質不能夠準確描述。因此,將分數階導數引入巖土蠕變模型建構中能描述這種勾兌特性,并發揮其參數少、形式簡單等優點。近年來,巖土工程領域越來越多地引用分數階微積分理論來描述不同巖土材料的力學特性。殷德順等[9]將Hollomon提出的金屬塑性拉伸變形方程式引入巖土工程中,并在分數階導數基礎上給出了恒應變率加載情況下的土應力應變關系。Hou等[10]考慮應力引起的強弱化效應對凍土蠕變的影響,提出了一種分數階蠕變本構模型。此外,一些學者還將分數階導數理論應用于元件模型中[11-14],得出了相關的分數階蠕變模型。

分析西安某煤礦黏土在不同溫度、不同含水率及加載應力下的單軸蠕變試驗曲線,得到其對凍結重塑黏土蠕變特性的影響規律。在經驗模型的基礎上引入分數階導數理論,建立凍結溫度、含水率和加載應力相互影響的人工凍結重塑黏土分數階蠕變模型。

1 人工凍土力學試驗

1.1 人工凍土單軸抗壓、蠕變試驗

所用土樣取自西安某煤礦黏土,取樣深度為10～20 m,將土樣加工成高度100 mm、直徑50 mm的圓柱體試樣(見圖1),用WDT-100型微機控制電液伺服凍土試驗機進行單軸抗壓試驗和單軸蠕變試驗[15]。試驗土樣物理性質指標參數見表1。

表1 試樣物理性質指標參數

(a)試驗前

(b)試驗后

1.2 試驗結果與分析

根據單軸抗壓強度試驗,得到凍結重塑黏土在3個含水率及不同溫度水平下的單軸抗壓強度,如表2所示。

表2 凍結重塑黏土單軸抗壓強度

凍結重塑黏土從加載到破壞的應力-應變關系主要經歷彈性階段,塑性階段和屈服破壞階段。彈性階段,隨著軸向應力的增大,使得土體密實度增加,土樣的承載能力提高,此階段的應力-應變曲線基本呈線性增長;塑性階段,隨著軸向應力的進一步增大,土體發生不可逆變形,曲線呈非線性增長趨勢,應力達到頂峰,土體內部產生裂隙,冰結晶與圖顆粒開始破壞;屈服破壞階段,應力達到頂峰后繼續加載,試樣承載能力降低,試樣進入軟化階段,且試樣隨凍結溫度的降低,單軸抗壓強度逐漸增大,結果如圖2所示。

圖2 不同條件下凍結重塑黏土應力-應變曲線

如圖3所示,凍結重塑黏土含水率分別為12%、16%和20%以及溫度為-5 ℃、-10 ℃和-15 ℃的條件下開展無側限單軸抗壓強度試驗,得到抗壓強度與含水率、凍結溫度間的關系圖,溫度、含水率和抗壓強度滿足

圖3 抗壓強度與含水率、凍結溫度關系

σs=-20-0.35T-760ω2+255ω,R2=0.98

(1)

隨著凍結重塑黏土含水率的增加,其強度呈先增大后降低趨勢,含水率約16%時強度達到最大。原因是在含水率處于較低水平時,含冰量的多少決定凍土的強度,同等溫度下,含水率增加導致含冰量相應增大,凍結重塑黏土顆粒間冰膠結力增大,內聚力增強,從而導致強度增大。當含水量達到最優含水率后,隨著水分含量增加,內部未凍水含量增多產生潤滑作用,導致黏土顆粒間摩阻力降低,強度下降。

2 人工凍土分數階蠕變模型

2.1 分數階微積分的定義

β是一個正實數,令n-1<β≤n,一個定義在[a,b]區間上的函數f(t)的β階分數階積分的定義是

(2)

它的另一個表達形式為

(3)

其中Γ(z)表示通常的Gamma函數,即

(4)

關于分數階微積分有很多定義,其中Riemann-Liouville分數階微積分算子理論對函數f(t)的β階分數階積分的定義為

(5)

對于函數f(x)=zx,z為常數,其分數階微分為

(6)

當取t=v0τ時,其中v0為常數,則

(7)

(8)

2.2 分數階蠕變模型的建立及參數確定

根據《人工凍土物理力學性能試驗》[16]可知,以冪函數的組合形式能夠描述人工凍土蠕變特性,建立經驗模型

(9)

式中:ε為軸向應變;T為凍結溫度,單位為℃;t為時間,單位為h;A、k、b、c均為模型參數,k、b、c分別反映了凍土變形發展受溫度、加載應力、時間影響的敏感性;σ=ησs;η為蠕變加載系數,為0.3或0.5;σs為單軸抗壓強度。

凍結重塑黏土的應力應變特性是介于理想固體和理想流體之間的某種關系,式(9)未能反映該種特性,而分數階導數能夠準確描述該種關系,對式(9)進行分數階微分得到

(10)

(11)

分別將各含水率、溫度和加載等級下的應變與時間取對數,發現在同一含水率和加載等級下,不同凍結溫度條件下的應變與時間取對數時具有線性關系,因此將各含水率下不同加載系數及不同溫度的試驗值分別代入建立的模型中,聯立方程組對模型參數進行求解。對式(11)兩邊同時取對數有

lgε=lgB+blgσ+βlg v0-lg Γ(2-β)+(1-β)lgt

(12)

圖4為對各含水率和不同溫度下的試樣進行加載,加載等級為0.3σs和0.5σs的lgε-lgt擬合關系。可以發現:

(1) 在圖4中,-5 ℃、-10 ℃、-15 ℃三個溫度下的lgε-lgt擬合曲線斜率近似平行,試樣蠕變變形值lgε隨著溫度的降低而減小。這是由于土中未凍水的含量逐漸減少,其抵抗變形的能力逐漸增大,蠕變變形值逐漸降低。

(2) 由圖4(b)、圖4(c)可以發現,加載系數不同而擬合曲線斜率同樣近似平行,相同含水率和溫度下,擬合曲線截距隨加載系數的增大而增大。

綜上,凍結重塑黏土蠕變的lgε-lgt擬合曲線斜率均近似相等,其截距的值與含水率、加載系數及溫度有關。

(a)含水率 12%,加載系數0.5

(c)含水率16%,加載系數0.5

(d)含水率20%,加載系數0.5

2.2.1 參數β的確定

含水率為12%時,加載系數0.3σs下,溫度分別為-5 ℃、-10 ℃、-15 ℃的線性表達式為

(13)

含水率為12%時,加載系數0.5σs下,溫度分別為-5 ℃、-10 ℃、-15 ℃的線性表達式為

(14)

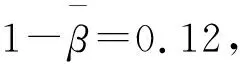
2.2.2 參數B和b的確定

lgB1+b1lg 0.3σs-lg Γ(2-β)=0.42

(15)

lgB1+b1lg 0.5σs-lg Γ(2-β)=0.75

(16)

計算出含水率為12%時,T=-5 ℃的參數B1、b1的值,B1=8.86,b1=1.49。

同理求出不同的含水率與加載系數對應的B和b的值(見表3)。

由表3及圖5、圖6可知,溫度與含水率對凍結重塑黏土蠕變特性均有較大影響。蠕變模型參數B的值隨著溫度的降低不斷減小,而b值變化不大。溫度-5 ℃時參數B在20%含水率下所得的值要小于在16%含水率下的值,表明在同種溫度條件下,接近最優含水率的凍結重塑黏土延性更大,達到破壞所需時間增加,導致蠕變推遲。大于最優含水率的凍結重塑黏土延性降低,達到破壞所需時間減少,加速蠕變提前。

表3 不同溫度、含水率條件下參數B和b的值

圖5 凍結重塑黏土參數B與溫度關系曲線

圖6 參數b(T,ω)三維擬合圖

由上述整理得,溫度T和含水率ω與B和b擬合關系式為

(17)

b=0.009 6T+12.96ω-0.068

(18)

將參數B和b代入式(11),得出與溫度和含水率有關的分數階凍結重塑黏土蠕變模型為

(19)

根據推導出的分數階凍結重塑黏土蠕變模型計算出該重塑黏土凍結狀態下的蠕變值,將計算得出的結果與試驗值對比,結果如圖7所示。

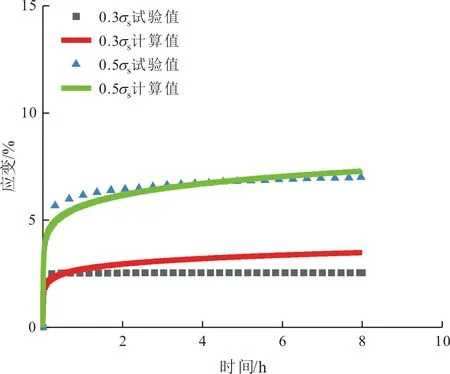
(a)溫度-5 ℃,含水率12%

(b)溫度-15 ℃,含水率12%

(c)溫度-15 ℃,含水率16%

(d)溫度-5 ℃,含水率20%

(e)溫度-10 ℃,含水率20%

由圖7可知,總體上該經驗模型計算值與試驗值吻合程度較高,對不同含水率、不同溫度及加載等級下凍結重塑黏土蠕變值模擬結果較為準確。其中圖7(e)和圖7(f)在0.5σs荷載等級下的試驗值與計算值出現偏差,分析原因可能是含水率較高,試樣內冰結晶的分布不均,且溫度越低,使得試樣中的冰結晶強度越大,造成單軸強度偏差越大,導致蠕變加載應力偏差越大,以致試驗值較計算值偏差越大。

3 結論與展望

鑒于以冪函數組合形式建立的經驗模型在描述人工凍土蠕變特性和確定模型參數等方面的不足,基于分數階導數理論,建立能在不同溫度、不同含水率及加載強度條件下的凍結重塑黏土分數階蠕變模型。所建模型具體結論如下:

(1) 通過在常見的蠕變模型中引入分數階導數,能夠很好地反映凍結黏土蠕變介于理性固體和理想流體之間的某種勾兌特性。

(2) 建立的凍結重塑黏土分數階蠕變模型參數在不同凍結溫度和含水率下,對不同加載應力產生的蠕變與時間取對數聯立方程均具有物理意義且易于確定,便于工程應用。

(3)所建凍結重塑黏土分數階蠕變模型計算結果曲線與試驗曲線吻合度較高,表明該模型能夠較好地描述凍結重塑黏土在單軸壓縮狀態下不同溫度和不同含水率的力學行為。

針對個別組分數階蠕變模型計算值和試驗值偏差較大的現象,將進一步完善試驗方案,如在蠕變試驗中增加0.7荷載等級加載和增加凍結溫度為-20 ℃的試驗,加大試驗量為下一步優化模型參數積累試驗數據。凍結重塑黏土蠕變特性除了受凍結溫度、含水率和加載應力影響外,還受損傷、固結壓力及應力歷史等因素的影響。因此,建立考慮凍結重塑黏土主要因素影響的分數階蠕變模型是下一步的研究目標,以便研究結果更好地服務實際工程。