基于應(yīng)變修正Arrhenius模型的Mg-3Al-3Sn-0.3Mn合金熱加工圖研究

戴莉莉，周璟怡，敬學(xué)銳，秦晨，佘加，湯愛濤

基于應(yīng)變修正Arrhenius模型的Mg-3Al-3Sn-0.3Mn合金熱加工圖研究

戴莉莉，周璟怡，敬學(xué)銳，秦晨，佘加，湯愛濤*

（重慶大學(xué) 材料科學(xué)與工程學(xué)院，重慶 400044）

以Mg-3Al-3Sn-0.3Mn（ATM3303）合金為研究對象，研究了一種使用少量基礎(chǔ)實(shí)驗(yàn)數(shù)據(jù)，獲得高精度低成本的熱加工圖的方法。利用少量熱壓縮實(shí)驗(yàn)獲取ATM3303合金的真應(yīng)力-應(yīng)變曲線，根據(jù)應(yīng)變修正的Arrhenius模型來分段擬合本構(gòu)方程。根據(jù)本構(gòu)方程可計(jì)算更多力學(xué)數(shù)據(jù)，以計(jì)算所得數(shù)據(jù)結(jié)合實(shí)驗(yàn)數(shù)據(jù)構(gòu)建拓展的熱加工圖；將該拓展熱加工圖與基于實(shí)驗(yàn)數(shù)據(jù)的普通熱加工圖進(jìn)行比較，通過驗(yàn)證實(shí)驗(yàn)判別2張熱加工圖的精度。相較于普通熱加工圖，經(jīng)本構(gòu)方程優(yōu)化的拓展熱加工圖內(nèi)，流變失穩(wěn)區(qū)的面積有所減小。普通熱加工圖內(nèi)的部分加工失穩(wěn)窗口，在拓展熱加工圖內(nèi)被預(yù)測為安全區(qū)。熱擠壓實(shí)驗(yàn)證實(shí)，ATM3303合金可在該工藝參數(shù)窗口下安全加工。在基礎(chǔ)實(shí)驗(yàn)條件外，本構(gòu)方程優(yōu)化的熱加工圖預(yù)測了一個(gè)失穩(wěn)區(qū)，實(shí)驗(yàn)顯示，ATM33303合金在該失穩(wěn)區(qū)進(jìn)行熱擠壓會形成粗大晶粒，持續(xù)加工可能引發(fā)失效。經(jīng)本構(gòu)方程優(yōu)化的拓展熱加工圖可較準(zhǔn)確地指導(dǎo)ATM3303合金的熱加工，數(shù)值計(jì)算結(jié)合實(shí)驗(yàn)是構(gòu)建高精度低成本熱加工圖的新方法。

鎂合金；流變行為；熱壓縮；熱加工圖；本構(gòu)方程

鎂合金作為21世紀(jì)的新型綠色結(jié)構(gòu)材料，被廣泛應(yīng)用于眾多工業(yè)領(lǐng)域。近年來，變形鎂合金Mg-3Al- 3Sn-0.3Mn（ATM3303, wt.pct）因其良好的耐蝕性和高溫綜合力學(xué)性能引發(fā)了廣泛的關(guān)注，在航空航天、交通運(yùn)輸?shù)阮I(lǐng)域前景廣闊[1-2]。然而，不適宜的工藝參數(shù)（溫度、應(yīng)變速率）會造成材料內(nèi)部組織缺陷，影響其工業(yè)應(yīng)用。因此，根據(jù)材料的變形行為來選擇ATM3303合金的機(jī)加工參數(shù)極為必要。

熱加工圖（Processing Map）是反映不同加工條件下材料可加工性的二維圖形，可用于選取最優(yōu)工藝參數(shù)。熱加工圖由功率耗散圖和流變失穩(wěn)圖疊加而成[3]。功率耗散圖是功率耗散率因子（）的等值線分布圖，其主要與合金的動態(tài)再結(jié)晶、開裂、絕熱剪切帶的形成等行為有關(guān)，它反映了封閉合金體系在加工過程中的微觀組織演化。流變失穩(wěn)圖以失穩(wěn)判據(jù)（）將工藝參數(shù)窗口劃分為流變失穩(wěn)區(qū)（<0）和加工安全區(qū)（>0），以此避免材料在加工時(shí)出現(xiàn)缺陷[4-5]。

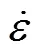
本構(gòu)方程（Constitutive Equation）是定量表達(dá)材料在變形過程中應(yīng)力、應(yīng)變、應(yīng)變速率、溫度關(guān)系的函數(shù)式。它可以基于少量實(shí)驗(yàn)數(shù)據(jù)，預(yù)測實(shí)驗(yàn)條件外（溫度、應(yīng)變速率）的材料形變應(yīng)力，是降低實(shí)驗(yàn)成本、擴(kuò)增材料力學(xué)數(shù)據(jù)量的有力工具，其精度對材料成形的模擬有極大的影響[13-16]。Arrhenius本構(gòu)模型是描述材料變形動態(tài)響應(yīng)的經(jīng)典方程，被應(yīng)用于諸多合金體系。然而，由于材料在不同溫區(qū)下的變形機(jī)制不同，在較大溫區(qū)下構(gòu)建的Arrhenius本構(gòu)方程的誤差較高[17-18]。例如，Nie等[19]構(gòu)建的Mg-9Gd-4Y-2Zn- 0.5Zr合金的應(yīng)變修正Arrhenius本構(gòu)方程的平均相對誤差為17.915%。Ma等[20]擬合了Mg-16Al合金的本構(gòu)方程，該方程在大應(yīng)變下的平均相對誤差為10.6%。馬立峰等[21]構(gòu)建了鑄態(tài)AZ31B合金的Arrhenius本構(gòu)方程，平均相對誤差為12.7%。這些研究得到的本構(gòu)方程的精度仍有待提升。有學(xué)者根據(jù)變形的微觀機(jī)理和材料的參數(shù)變化特征對本構(gòu)方程進(jìn)行分段。Liu等[22]根據(jù)第二相的溶解溫度，將溫區(qū)分為1 060～1 141 ℃和1 150～1 180 ℃，分段擬合了Ni-Co合金在γ單相區(qū)和γ＋γ’雙相區(qū)的本構(gòu)方程；Liu等[23]根據(jù)熱變形過程中材料參數(shù)的變化特征，構(gòu)建了T2純銅的分段本構(gòu)方程。本研究根據(jù)鎂合金的變形機(jī)制，將溫區(qū)分段為473～523、523～573、573～673 K 3個(gè)區(qū)間，對不同溫區(qū)下ATM3303合金的Arrhenius本構(gòu)方程分別進(jìn)行擬合。根據(jù)分段的本構(gòu)方程，可預(yù)估ATM3303合金在實(shí)驗(yàn)條件外的流變應(yīng)力，將本構(gòu)方程擴(kuò)增的數(shù)據(jù)與力學(xué)實(shí)驗(yàn)的數(shù)據(jù)相結(jié)合，可構(gòu)建本構(gòu)方程優(yōu)化的拓展熱加工圖。

1 實(shí)驗(yàn)

研究采用的ATM3303合金的名義成分如表1所示。將ATM3303合金鑄錠在673 K下均勻化處理24 h后，切割為8 mm×12 mm的試樣。在Gleeble實(shí)驗(yàn)機(jī)上對ATM3303合金試樣進(jìn)行不同溫度（473、523、573、623、673 K）、不同應(yīng)變速率（0.001、0.010、0.100、1.000 s?1）的Gleeble實(shí)驗(yàn)，共計(jì)20組，熱壓縮結(jié)束后的材料立即進(jìn)行水冷，實(shí)驗(yàn)?zāi)＞吆团髁暇捎檬珴櫥?/p>

表1 ATM3303合金名義成分

Tab.1 Nominal composition of ATM3303 alloy wt.%

2 結(jié)果與分析

2.1 真應(yīng)力-應(yīng)變曲線的修正

在熱加工過程中，材料塑性變形的一部分能量轉(zhuǎn)變?yōu)闊崮埽辉谳^高速率的熱變形過程中，由于變形時(shí)間短，熱量無法完全從材料中傳導(dǎo)出去，導(dǎo)致材料內(nèi)部溫度上升，產(chǎn)生絕熱溫升效應(yīng)。因此，需要對ATM3303合金在應(yīng)變速率為1 s?1時(shí)的真應(yīng)力-應(yīng)變曲線進(jìn)行修正[24]。

在熱變形過程中，絕熱溫升引起的溫度變化量Δ可表達(dá)為[25]：

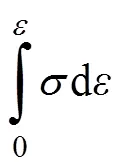
根據(jù)式（1），可計(jì)算出ATM3303合金在應(yīng)變速率1 s?1時(shí)，不同預(yù)設(shè)溫度下熱壓縮時(shí)的絕熱溫升情況，如圖1a所示。由圖1a可見，隨著應(yīng)變量的增加，塑性變形產(chǎn)生的熱量難以全部傳導(dǎo)出去，ATM3303合金內(nèi)部的溫度持續(xù)上升。在相同應(yīng)變量下，預(yù)設(shè)的變形溫度越低，變形導(dǎo)致的溫升量Δ越大。

絕熱溫升導(dǎo)致實(shí)際變形溫度高于預(yù)設(shè)變形溫度，引起材料流變應(yīng)力的下降。流變應(yīng)力下降的幅度Δ與變形溫升量Δ的關(guān)系可表達(dá)為：

絕熱溫升修正后的流變曲線如圖2所示。在變形初期，ATM3303合金的真應(yīng)力因加工硬化迅速增大；隨后，在動態(tài)再結(jié)晶的軟化作用下，真應(yīng)力達(dá)峰值后逐漸降低；在變形后期，加工硬化與再結(jié)晶軟化達(dá)到動態(tài)平衡，真應(yīng)力趨于平穩(wěn)。

鎂合金的再結(jié)晶溫區(qū)通常在523～573 K。在473～ 523 K下熱加工時(shí)，鎂合金開啟基面、柱面滑移系，動態(tài)再結(jié)晶程度較低。在中溫區(qū)間（523～573 K），鎂合金的熱變形機(jī)制通常較為復(fù)雜；在低應(yīng)變速率下，變形時(shí)間較長，動態(tài)再結(jié)晶程度有所上升，導(dǎo)致晶粒尺寸分布不均勻，嚴(yán)重影響塑性；而在中溫區(qū)的高應(yīng)變速率下熱加工時(shí)，由于變形時(shí)間極短，除了已開啟的基面和柱面滑移系外，孿晶機(jī)制被激活，合金塑性較好[30-31]。在溫度高于573 K時(shí)，除基面、柱面滑移系外，鎂合金還會開啟二級錐面滑移系[32-33]，此時(shí)材料的動態(tài)再結(jié)晶程度較高，表現(xiàn)出良好的塑性變形能力，表現(xiàn)為熱壓縮曲線上不同程度的再結(jié)晶軟化，如圖2d～e。因此，本研究根據(jù)鎂合金的變形機(jī)制，將變形溫度分成473～523、523～573、573～673 K 3個(gè)區(qū)間，進(jìn)行本構(gòu)方程的分段擬合。

2.2 應(yīng)變修正的Arrhenius本構(gòu)方程

在塑性變形中，可通過本構(gòu)方程定量描述流變應(yīng)力與變形溫度、應(yīng)變速率、應(yīng)變量之間的關(guān)系。下文以573～673 K溫區(qū)、應(yīng)變量為0.4的數(shù)據(jù)為例，介紹本構(gòu)方程的具體擬合流程。

圖1 應(yīng)變速率為1 s–1時(shí)，ATM3303合金的變形溫升和真應(yīng)力-應(yīng)變曲線的溫度修正

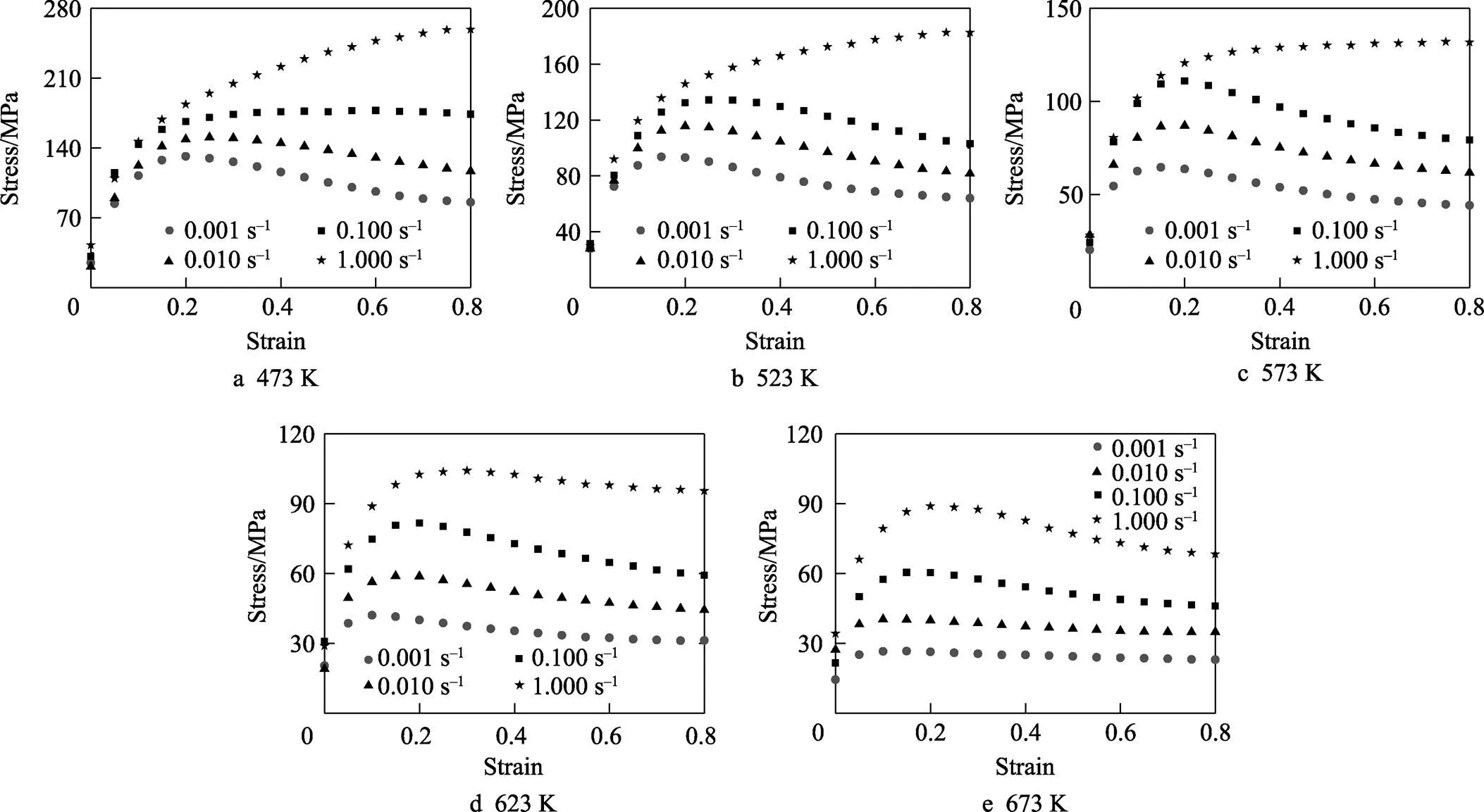
圖2 經(jīng)溫度修正后，ATM3303合金在不同變形溫度下的真應(yīng)力-應(yīng)變曲線

合金中最常見的本構(gòu)方程是Arrhenius方程，其表達(dá)式為：

以泰勒公式展開式（3）中的雙曲正弦函數(shù)并化簡，可得：

對式（3）～（5）取對數(shù)，分別可得：

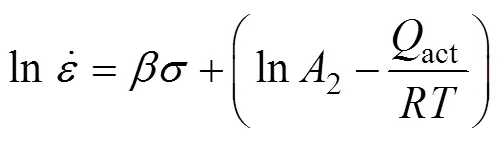
對式（6）進(jìn)行偏微分，可得到變形激活能act的表達(dá)式：

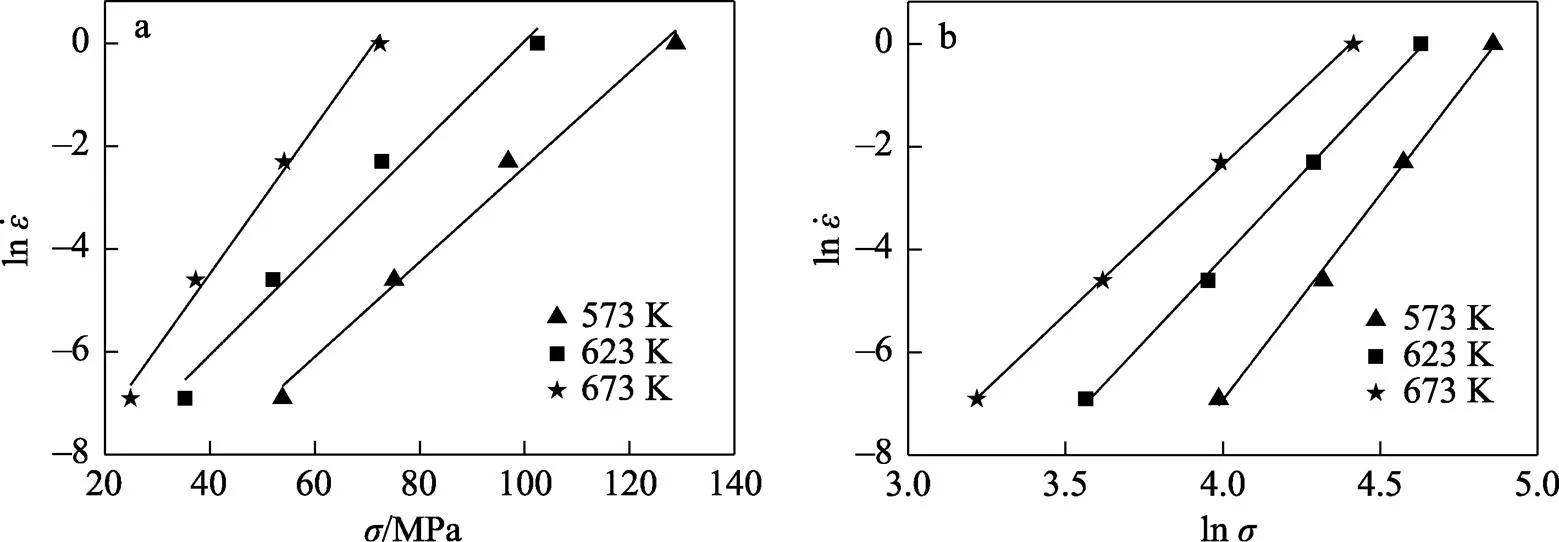
圖3 應(yīng)變?yōu)?.4時(shí)，和的擬合曲線

圖4 應(yīng)變?yōu)?.4時(shí)，和的擬合曲線

溫度補(bǔ)償速率因子可衡量不同變形參數(shù)下材料的本征可加工性，其表達(dá)式為：

對式（10）兩邊同取對數(shù)，可得：

圖5 應(yīng)變?yōu)?.4時(shí)，的線性擬合

對式（3）進(jìn)行整理，得到流變應(yīng)力與應(yīng)變速率、變形溫度和材料參數(shù)的關(guān)系式：

當(dāng)溫度、應(yīng)變速率已知時(shí)，材料常數(shù)、、act、ln均可根據(jù)式（12）～（15）求出。根據(jù)式（16），可預(yù)測ATM3303合金在不同工藝參數(shù)下的流變應(yīng)力。本文獲取的分段的應(yīng)變修正Arrhenius本構(gòu)方程的預(yù)測效果如圖7所示，虛線代表預(yù)測的流變曲線。

為定量描述本構(gòu)方程的準(zhǔn)確性，以平均絕對相對誤差（Average Absolute Relative Error，AARE）對分段的應(yīng)變修正Arrhenius本構(gòu)方程進(jìn)行評估。AARE的計(jì)算公式如下：

2.3 ATM3303合金的熱加工圖

在熱加工過程中，外界輸入材料內(nèi)部的能量主要被轉(zhuǎn)化為熱能和組織演變能。Prasad等[34]基于不可逆熱力學(xué)原理和大塑性變形連續(xù)介質(zhì)力學(xué)構(gòu)建的動態(tài)材料模型（Dynamic Material Model, DMM），可以較為準(zhǔn)確地描述材料在塑性變形過程中的組織變化、局部流變等行為。

圖6 八次多項(xiàng)式擬合的材料常數(shù)

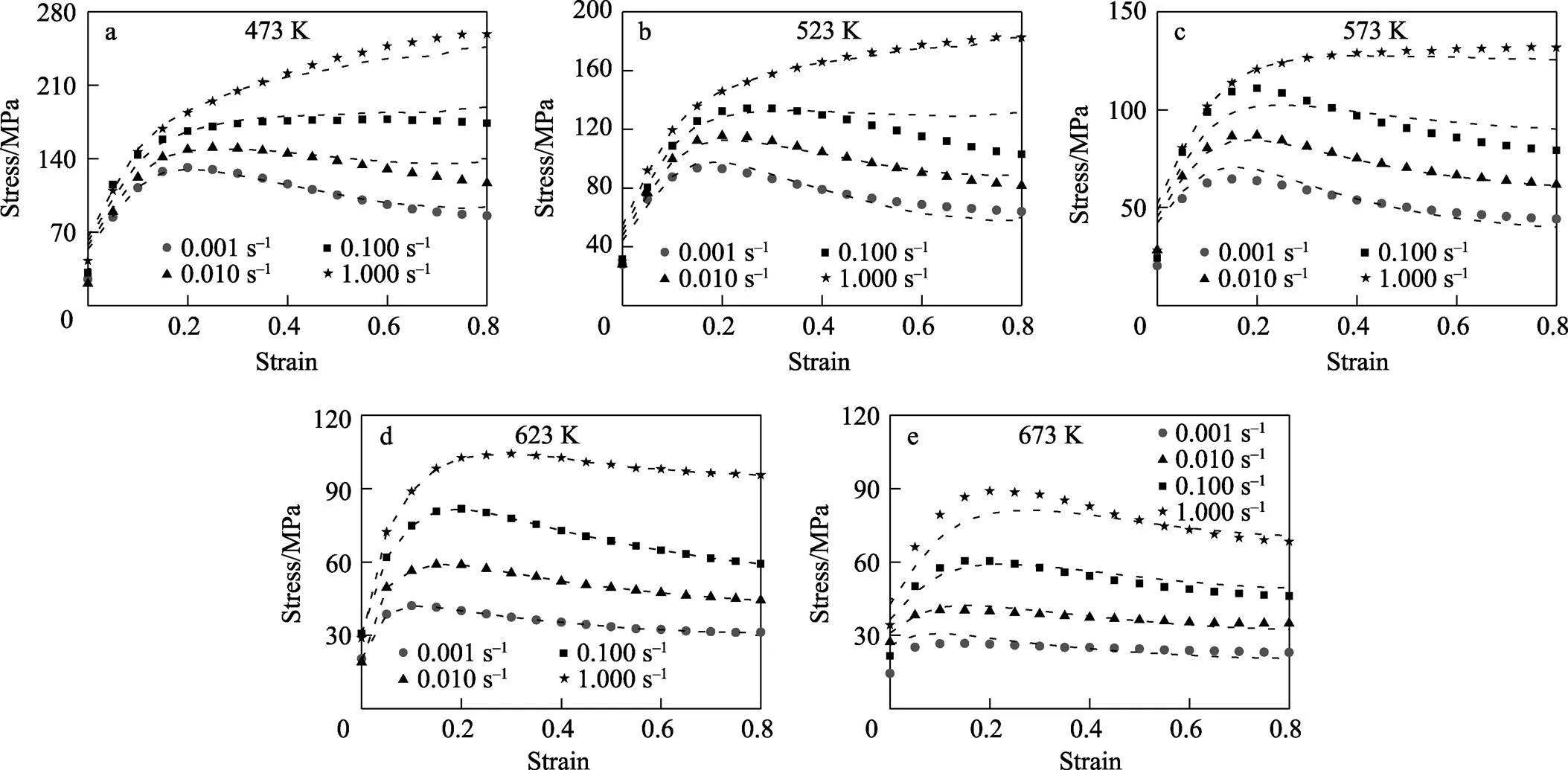
圖7 實(shí)驗(yàn)流變應(yīng)力與本構(gòu)方程預(yù)測的流變應(yīng)力的對比

表2 本構(gòu)方程的平均絕對相對誤差分布

Tab.2 AARE distribution of constitutive equations %

DMM將材料視作非線性封閉能量耗散器，在塑性變形中，單位時(shí)間內(nèi)外界輸入該能量耗散器的功率（）主要有2個(gè)耗散部分。一部分是耗散量（），即材料發(fā)生塑性變形所消耗的能量，該部分能量轉(zhuǎn)化為熱能；另一部分為耗散協(xié)量（），主要與組織演變相關(guān)。封閉合金系統(tǒng)的能量轉(zhuǎn)化滿足守恒律，即：

材料變形的真應(yīng)力可以表示為：

式中：為應(yīng)力系數(shù)；是應(yīng)變速率敏感指數(shù)，與耗散量（）和耗散協(xié)量（）的分配比例有關(guān)。應(yīng)變速率敏感指數(shù)的計(jì)算公式如下：

功率耗散率因子（）可衡量材料在變形過程中的組織變化程度，其計(jì)算式為：

功率耗散率因子越大，材料組織演變所耗散的功率越高，微觀組織變化的程度就越劇烈。

Ziegler[35]基于最大熵增原理指出，DMM的熵增速率應(yīng)與外界做功的熵增速率相匹配，否則材料將在加工中發(fā)生流變失穩(wěn)，形成空洞、裂紋等缺陷[3]。材料在塑性變形中發(fā)生流變失穩(wěn)的判據(jù)為：

式中：為耗散函數(shù)，是等效應(yīng)變速率。Prasad等[3]以耗散協(xié)量（）代替式（22）中的耗散函數(shù)（），得到失穩(wěn)判據(jù)（），其計(jì)算公式為：

一般認(rèn)為，當(dāng)失穩(wěn)判據(jù)＜0時(shí)，材料發(fā)生流變失穩(wěn)，持續(xù)加工可能形成空洞、裂紋等缺陷。

根據(jù)材料的流變應(yīng)力，可計(jì)算出不同工藝參數(shù)下的功率耗散率因子（）和失穩(wěn)判據(jù)（）。功率耗散率因子用于衡量材料微觀組織的變化程度；失穩(wěn)判據(jù)可防止材料在加工過程中產(chǎn)生空洞、裂紋、絕熱剪切帶等缺陷；二者疊加形成了合金的熱加工圖。

基于熱壓縮實(shí)驗(yàn)的數(shù)據(jù)，可計(jì)算ATM3303合金的應(yīng)變速率敏感指數(shù)（），基于應(yīng)變速率敏感指數(shù)可計(jì)算出合金的功率耗散率因子（），功率耗散因子可用于繪制功率耗散圖，即圖8a中的黑色等高線。根據(jù)應(yīng)變速率敏感指數(shù)（），也可計(jì)算得到失穩(wěn)判據(jù)（），根據(jù)失穩(wěn)判據(jù)可繪制ATM3303合金在不同應(yīng)變下的流變失穩(wěn)圖，如圖8a灰色區(qū)域所示。僅基于實(shí)驗(yàn)數(shù)據(jù)計(jì)算出的功率耗散圖和流變失穩(wěn)圖，共同構(gòu)成了ATM3303合金的普通熱加工圖。

本構(gòu)方程是獲取實(shí)驗(yàn)條件外的材料流變應(yīng)力的有力工具。根據(jù)前文獲取的應(yīng)變修正Arrhenius本構(gòu)方程，分別計(jì)算ATM3303合金在實(shí)驗(yàn)條件外（變形溫度498、548、598、648、698、723 K，應(yīng)變速率0.001、0.010、0.100、0.500、1.000 s?1）的流變應(yīng)力。將實(shí)驗(yàn)的數(shù)據(jù)集和本構(gòu)方程的數(shù)據(jù)集相結(jié)合，構(gòu)建本構(gòu)方程優(yōu)化后的拓展熱加工圖，如圖8b所示。

對比2張熱加工圖，經(jīng)本構(gòu)方程優(yōu)化的拓展熱加工圖內(nèi)的灰色失穩(wěn)區(qū)的面積有所減小。工藝參數(shù)窗口在普通熱加工圖內(nèi)被判定為失穩(wěn)區(qū)，而在本構(gòu)方程優(yōu)化的拓展熱加工圖內(nèi)則為安全加工區(qū)。此外，由于本構(gòu)方程獲取了實(shí)驗(yàn)條件外的材料熱變形的應(yīng)力數(shù)據(jù)，拓展熱加工圖預(yù)測ATM3303合金在工藝參數(shù)窗口下加工時(shí)，易出現(xiàn)流變失穩(wěn)現(xiàn)象。

2.4 熱加工圖的應(yīng)用與驗(yàn)證

為驗(yàn)證熱加工圖的準(zhǔn)確性，分別在圖8所示的工藝參數(shù)窗口、、下進(jìn)行熱擠壓實(shí)驗(yàn)，實(shí)驗(yàn)條件如表3所示。鑄態(tài)ATM3303合金先在673 K下均勻化處理24 h。將均勻化后的合金在目標(biāo)溫度下保溫10 min，根據(jù)選定的應(yīng)變速率進(jìn)行熱擠壓后，立即水冷淬火以保留變形組織。沿著垂直于擠壓的方向切割熱壓縮后的試樣，分別以240、800、1200目的砂紙打磨，再用苦味酸進(jìn)行腐蝕，通過金相顯微鏡觀察不同工藝參數(shù)下熱加工的顯微組織，如圖9所示。

圖9a是均勻化處理的ATM3303合金的金相組織。在工藝參數(shù)窗口區(qū)擠壓的ATM3303合金的微觀組織如圖9b所示，該工藝參數(shù)對應(yīng)的功率耗散率因子較高，制備的合金晶粒細(xì)小，再結(jié)晶程度較高。

圖8 ATM3303合金的熱加工圖

圖9 不同參數(shù)下熱加工的ATM3303合金的顯微組織

表3 根據(jù)熱加工圖選定的工藝參數(shù)

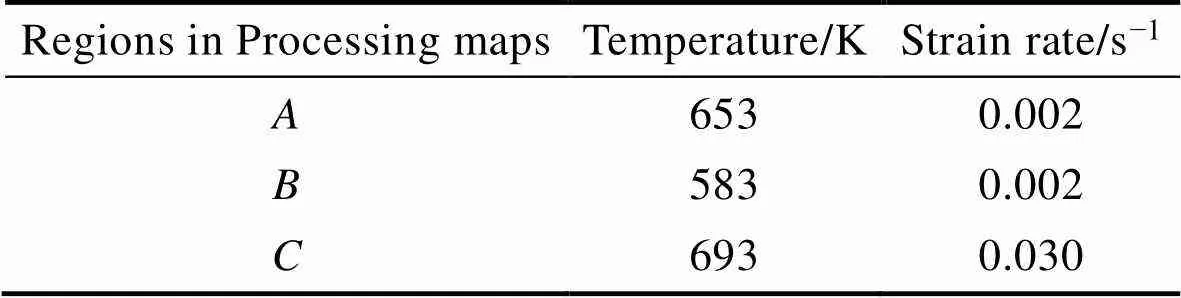
Tab.3 Processing parameters selected by processing maps

在本構(gòu)方程優(yōu)化后的熱加工圖內(nèi)，區(qū)為加工安全區(qū)，而在普通熱加工圖中，區(qū)被判定為失穩(wěn)窗口，這可能源于區(qū)較低的失穩(wěn)判據(jù)值。Chiba等[36]結(jié)合實(shí)驗(yàn)指出，失穩(wěn)判據(jù)值在?0.2～0時(shí)，所對應(yīng)的參數(shù)窗口是材料的亞穩(wěn)加工區(qū)，在該類區(qū)間下的加工失穩(wěn)現(xiàn)象不會特別顯著。使用B區(qū)域內(nèi)的工藝參數(shù)（583 K，0.002 s?1）對ATM3303合金進(jìn)行熱擠壓實(shí)驗(yàn)，材料的金相組織如圖9c所示，可見合金內(nèi)部晶粒較細(xì)小，未形成加工缺陷。這證實(shí)了區(qū)是ATM3303合金的安全加工區(qū)，經(jīng)本構(gòu)方程優(yōu)化的熱加工圖的精度更高。

在圖8b中，工藝參數(shù)窗口區(qū)是流變失穩(wěn)區(qū)，在該條件下加工的ATM3303合金的微觀組織如圖9d所示。由于區(qū)是高溫高應(yīng)變速率的工藝參數(shù)窗口，在熱加工時(shí)，封閉合金系統(tǒng)內(nèi)的大部分塑性變形功轉(zhuǎn)變?yōu)闊崮埽叶虝r(shí)間內(nèi)無法全部傳導(dǎo)出系統(tǒng)，故ATM3303合金內(nèi)部儲存能較高；由于儲存能大且再結(jié)晶孕育期短，部分合金晶粒生長速度快于其他晶粒，材料整體晶粒尺寸較為不均，宏觀上易形成混晶組織[37-38]，降低材料性能。持續(xù)在該區(qū)間加工，合金內(nèi)部可能形成空洞、裂紋、絕熱剪切帶等缺陷[39-40]。

綜上所述，利用應(yīng)變修正的本構(gòu)方程制備較高精度的熱加工圖，一方面有利于更加精確地篩選材料的加工變形參數(shù)；另一方面可以輔助識別材料性能異常的工藝參數(shù)，為相關(guān)機(jī)理的研究提供出發(fā)點(diǎn)。

3 結(jié)論

本文基于ATM3303合金的熱壓縮試驗(yàn)，研究了該合金在溫度473～673 K，應(yīng)變速率0.001～1.000 s?1下的流變行為，具體結(jié)論如下：

1）基于溫度分段構(gòu)建了ATM3303合金的應(yīng)變修正Arrhenius本構(gòu)方程，該方程的平均絕對相對誤差為5.066%，能夠?qū)TM3303合金的流變應(yīng)力進(jìn)行較為準(zhǔn)確的預(yù)測。

2）以本構(gòu)方程優(yōu)化的拓展熱加工圖顯示：在應(yīng)變速率小于0.015 s?1時(shí)，ATM3303合金的變形溫度窗口較寬，在543～723 K下變形，均不會失穩(wěn)。因此，在對ATM3303合金進(jìn)行低溫加工時(shí)，可選擇543～ 573 K、應(yīng)變速率0.015 s?1作為變形工藝參數(shù)。

3）實(shí)驗(yàn)證實(shí)，相比于傳統(tǒng)熱加工圖，以本構(gòu)方程優(yōu)化的熱加工圖的適用溫區(qū)更廣，可根據(jù)需求進(jìn)行拓展。

[1] 潘復(fù)生, 蔣斌. 鎂合金塑性加工技術(shù)發(fā)展及應(yīng)用[J]. 金屬學(xué)報(bào), 2021, 57(11): 1362-1379.

PAN F S, JIANG B. Development and Application of Plastic Processing Technologies of Magnesium Alloys[J]. Acta Metallurgica Sinica, 2021, 57(11): 1362- 1379.

[2] SHE J, PAN F, ZHANG J, et al. Microstructure and Mechanical Properties of Mg–Al–Sn Extruded Alloys[J]. Journal of Alloys and Compounds, 2016, 657: 893-905.

[3] PRASAD Y V R K, SASIDHARA S. Hot Working Guide: A Compendium of Processing Maps[M]. Ohio: ASM Intennational, 2015.

[4] GUO S L, SHEN Y Z, GUO J T, et al. An Investigation on the Hot Workability and Microstructural Evolution of a Novel Dual-Phase Mg-Li Alloy by Using 3D Processing Maps[J]. Journal of Materials Research and Technology, 2023, 23: 5486-5501.

[5] ZHANG L, WU X Y, ZHANG X F, et al. Constitutive Model and Recrystallization Mechanism of Mg-8.7Gd- 4.18Y-0.42Zr Magnesium Alloy during Hot Deformation[J]. Materials, 2022, 15(11): 3914.

[6] ZHI C C, LEI J Y, XING H W, et al. Tensile Fracture Prediction of AZ31 Cast-Rolled Sheet Based on Hot Working Map[J]. Journal of Materials Research and Technology, 2023, 23: 3272-3283.

[7] LUO R, ZHOU Y M, GAO P, et al. Characterization of Hot Workability of IN617B Alloy Using Activation Energy, Zener-Hollomon Parameter and Hot Processing Maps[J]. Journal of Materials Research and Technology, 2023, 26: 5141-5150.

[8] XUE T X, YU J B, WANG Z, et al. Investigation on Hot Workability of Fe-6.5Si-2Cr-12Ni High-Silicon Steel Based on Processing Map and Microstructural Evolution[J]. Metallurgical and Materials Transactions A, 2023, 54(6): 2227-2243.

[9] REZAEI A, MAHMUDI R, LOGE R. Effect of Ag Addition on the Hot Deformation, Constitutive Equations and Processing Maps of a Hot Extruded Mg-Gd-Y Alloy[J]. Metallurgical and Materials Transactions A, 2020, 51(10): 5139-5153.

[10] SUTTON S C, LUO A A. Constitutive Behavior and Processing Maps of a New Wrought Magnesium Alloy ZE20 (Mg-2Zn-0.2Ce)[J]. Journal of Magnesium and Alloys, 2020, 8(1): 111-126.

[11] 支盛興, 李興剛, 袁家偉, 等. 擠壓態(tài)AZ40鎂合金熱變形行為及熱加工圖分析[J]. 材料工程, 2021, 49(11): 136-146.

ZHI S X, LI X G, YUAN J W, et al. Analysis of Hot Deformation Behavior and Processing Map of Extruded AZ40 Alloy[J]. Journal of Materials Engineering, 2021, 49(11): 136-146.

[12] YANG W L, SHAO B, ZHOU P W, et al. Investigation on Improved Hot Processing Map of Cr4Mo4Ni4V Aerospace Bearing Steel Based on Carbide Content[J]. Advanced Engineering Materials, 2023, 25(13): 1-12.

[13] 楊川, 劉小濤, 司家勇, 等. 粉末冶金高溫合金FGH96的熱加工圖及熱壓縮變形過程的開裂行為[J]. 中國有色金屬學(xué)報(bào), 2015, 25(10): 2707-2719.

YANG C, LIU X T, SI J Y, et al. Processing Map and Cracking Behavior of Powder Metallurgy Superalloy FGH96 during Hot Compression[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(10): 2707-2719.

[14] 高文理, 關(guān)宇飛. 5083鋁合金熱壓縮應(yīng)力-應(yīng)變曲線修正與熱加工圖[J]. 中國有色金屬學(xué)報(bào), 2018, 28(9): 1737-1745.

GAO W L, GUAN Y F. Correction of Flow Stress-Strain Curve and Processing Maps of 5083 Aluminum Alloy during Hot Compression[J]. The Chinese Journal of Nonferrous Metals, 2018, 28(9): 1737-1745.

[15] HU L, LANG M W, SHI L X, et al. Study on Hot Deformation Behavior of Homogenized Mg-8.5Gd-4.5Y- 0.8Zn-0.4Zr Alloy Using a Combination of Strain-Com-pensated Arrhenius Constitutive Model and Finite Element Simulation Method[J]. Journal of Magnesium and Alloys, 2023, 11(3): 1016-1028.

[16] LIU L J, WU W G, ZHAO Y J, et al. Subroutine Embedding and Finite Element Simulation of the Improved Constitutive Equation for Ti6Al4V during High-Speed Machining[J]. Materials, 2023, 16(9): 3344.

[17] WANG J, XIAO G Q, ZHANG J S. A New Constitutive Model and Hot Processing Map of 5A06 Aluminum Alloy Based on High-Temperature Rheological Behavior and Higher-Order Gradients[J]. Materials Today Communications, 2023, 36: 106502.

[18] HE Z T, XU C. Simulation on High Strain Rate Thermal Deformation Constitutive Equation of AZ91 Magnesium Alloy[J]. Journal of Physics: Conference Series, 2023, 2459(1): 012018.

[19] NIE Y, ZHENG J, HAN R, et al. Hot Deformation Behaviour and Constitutive Equation of Mg-9Gd-4Y-2Zn- 0.5Zr Alloy[J]. Materials, 2022, 15(5): 1779.

[20] MA Z W, HU F Y, WANG Z J, et al. Constitutive Equation and Hot Processing Map of Mg-16Al Magnesium Alloy Bars[J]. Materials, 2020, 13(14): 3107.

[21] 馬立峰, 賈偉濤, 黃志權(quán), 等. 鑄態(tài)AZ31B鎂合金高溫變形行為數(shù)學(xué)建模[J]. 中南大學(xué)學(xué)報(bào)(自然科學(xué)版), 2017, 48(12): 3193-3199.

MA L F, JIA W T, HUANG Z Q, et al. Mathematical Modeling about As-Cast AZ31B Magnesium Alloy Deformation under High Temperature[J]. Journal of Central South University (Science and Technology), 2017, 48(12): 3193-3199.

[22] LIU P, ZHANG R, YUAN Y, et al. Hot Deformation Behavior and Workability of a Ni–Co Based Superalloy[J]. Journal of Alloys and Compounds, 2020, 831: 154618.

[23] LIU Y, XIONG W, YANG Q, et al. Constitutive Behavior and Processing Map of T2 Pure Copper Deformed from 293 to 1073K[J]. Journal of Materials Engineering and Performance, 2018, 27(4): 1812-1824.

[24] 尚麗梅, 王春旭, 韓順, 等. 基于摩擦-溫度雙修正的Maraging250鋼熱變形行為及熱加工圖[J]. 金屬熱處理, 2021, 46(5): 111-117.

SHANG L M, WANG C X, HAN S, et al. Hot Deformation Behavior and Processing Maps of Maraging250 Steel Based on Friction and Temperature Double Correction[J]. Heat Treatment of Metals, 2021, 46(5): 111-117.

[25] MATAYA M C, SACKSCHEWSKY V E. Effect of Internal Heating during Hot Compression on the Stress- Strain Behavior of Alloy 304L[J]. Metallurgical and Materials Transactions A, 1994, 25(12): 2737-2752.

[26] 李昌民, 譚元標(biāo), 趙飛. Inconel 718高溫合金流變曲線修正及熱加工圖[J]. 稀有金屬, 2020, 44(6): 585-596.

LI C M, TAN Y B, ZHAO F. Modification of Flow Stress Curve and Processing Maps of Inconel 718 Superalloy[J]. Chinese Journal of Rare Metals, 2020, 44(6): 585-596.

[27] 全澤鑫, 王朝輝, 杜文博, 等. B30銅鎳合金的高溫?zé)嶙冃涡袨榧凹庸D[J]. 材料工程, 2023, 51(7): 215- 226.

QUAN Z X, WANG Z H, DU W B, et al. Hot Deformation Behavior and Processing Map of B30 Copper- Nickel Alloy[J]. Journal of Materials Engineering, 2023, 51(7): 215-226.

[28] YUAN G Y, YOU G Q, BAI S L, et al. Effects of Heat Treatment on the Thermal Properties of AZ91D Magnesium Alloys in Different Casting Processes[J]. Journal of Alloys and Compounds, 2018, 766: 410-416.

[29] 曾小勤, 王杰, 應(yīng)韜, 等. 鎂及其合金導(dǎo)熱研究進(jìn)展[J]. 金屬學(xué)報(bào), 2022, 58(4): 400-411.

ZENG X Q, WANG J, YING T, et al. Recent Progress on Thermal Conductivity of Magnesium and Its Alloys[J]. Acta Metallurgica Sinica, 2022, 58(4): 400-411.

[30] 范永革, 汪凌云. AZ31鎂合金的中溫流變失穩(wěn)特征[J]. 中國有色金屬學(xué)報(bào), 2005, 15(10): 1602-1606.

FAN Y G, WANG L Y. Instability Flow Characteristics of AZ31 Magnesium Alloy at Moderate Temperature[J]. The Chinese Journal of Nonferrous Metals, 2005, 15(10): 1602-1606.

[31] PONGE D, GOTTSTEIN G. Necklace Formation during Dynamic Recrystallization: Mechanisms and Impact on Flow Behavior[J]. Acta Materialia, 1998, 46(1): 69-80.

[32] 余琨, 黎文獻(xiàn), 王日初. 鎂合金塑性變形機(jī)制[J]. 中國有色金屬學(xué)報(bào), 2005, 15(7): 1081-1086.

YU K, LI W X, WANG R C. Plastic Deformation Mechanism of Magnesium Alloys[J]. The Chinese Journal of Nonferrous Metals, 2005, 15(7): 1081-1086.

[33] TEHRANCHI A, YIN B, CURTIN W A. Solute Streng-thening of Basal Slip in Mg Alloys[J]. Acta Materialia, 2018, 151: 56-66.

[34] PRASAD Y V R K, GEGEL H L, DORAIVELU S M, et al. Modeling of Dynamic Material Behavior in Hot Deformation: Forging of Ti-6242[J]. Metallurgical Transactions A, 1984, 15(10): 1883-1892.

[35] ZIEGLER H. Progress in Solid Mechanics[M]. New York: John Wiely and Sons, 1963: 102-174.

[36] CHIBA A, LEE S H, MATSUMOTO H, et al. Construction of Processing Map for Biomedical Co–28Cr–6Mo– 0.16N Alloy by Studying Its Hot Deformation Behavior Using Compression Tests[J]. Materials Science and Engineering: A, 2009, 513/514: 286-293.

[37] 尹振入, 盧立偉, 劉曉燁, 等. 預(yù)孿晶AQ80鎂合金熱壓縮本構(gòu)方程及熱加工圖[J]. 中國有色金屬學(xué)報(bào), 2018, 28(8): 1523-1531.

YIN Z R, LU L W, LIU X Y, et al. Constitutive Equation and Processing Map of Hot Deformation for Pre-Twin AQ80 Magnesium Alloy[J]. The Chinese Journal of Nonferrous Metals, 2018, 28(8): 1523-1531.

[38] LING M, ZHANG Z S, LIANG Y L, et al. Hot-Working Properties of Ni-Based Superalloy GH4169 in Different Initial States[J]. Journal of Materials Engineering and Performance, 2022, 31(8): 6333-6348.

[39] 陳前, 王巖. δ相時(shí)效態(tài)GH4169合金的熱加工行為[J]. 中國有色金屬學(xué)報(bào), 2015, 25(10): 2727-2737.

CHEN Q, WANG Y. Hot Working Behavior of Delta- Processed GH4169 Alloy[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(10): 2727-2737.

[40] ZHANG Y Q, JIANG S Y, ZHAO Y N, et al. Constitutive Equation and Processing Map of Equiatomic NiTi Shape Memory Alloy under Hot Plastic Deformation[J]. Transactions of Nonferrous Metals Society of China, 2016, 26(8): 2152-2161.

Processing Maps of Mg-3Al-3Sn-0.3Mn Alloy Based on the Strain-compensated Arrhenius Model

DAI Lili, ZHOU Jingyi, JING Xuerui, QIN Chen, SHE Jia, TANG Aitao*

(College of Material Science and Engineering, Chongqing University, Chongqing 400044, China)

The work aims toinvestigate a low-cost method of obtaining a high-precision processing map with limited experimental data focusing on Mg-3Al-3Sn-0.3Mn (ATM3303) alloy. Based on the true strain-stress curves acquired from a few basic hot compression experiments, strain-compensated Arrhenius constitutive equations of ATM3303 alloy were figured out piecewise, which could predict more rheological stress of ATM3303 alloy in a wider processing range. The extended processing map of ATM3303 alloy was constructed with a combination of derived data and experimental data. The extended processing map was compared with the normal processing map constructed by only experimental data, and validation experiments were applied to reveal the precision of the two maps. Compared with the normal processing map, the instability area was smaller in the extended processing map optimized by constitutive equations. An unstable region in the normal processing map was predicted as a safe domain in the extended processing map. Hot compression experiments confirmed that the region was suitable for the hot processing of ATM3303 alloy. Furthermore, the extended processing map predicted an extra unstable region away from basic experimental conditions. Validation experiments showed that coarse grains were formed in ATM3303 alloy when processed under these conditions, and continuous processing might lead to material failure. In conclusion, the extended processing map optimized by constitutive equations can guide the hot processing of ATM3303 alloy more accurately, and it provides a new method for constructing high-precision and low-cost processing maps by the combination of numerical calculation and experiments.

magnesium alloy; rheological behavior; hot compression; processing maps; constitutive equations

10.3969/j.issn.1674-6457.2024.02.002

TG146.2

A

1674-6457(2024)02-0010-10

2023-09-13

2023-09-13

國家自然科學(xué)基金重點(diǎn)項(xiàng)目（51971042）；重慶市院士專項(xiàng)基金（cstc2018jcyj-yszxX0007）

The National Natural Science Foundation of China(51971042); The Academician Fund of Chongqing (cstc2018 jcyj-yszxX0007)

戴莉莉, 周璟怡, 敬學(xué)銳, 等. 基于應(yīng)變修正Arrhenius模型的Mg-3Al-3Sn-0.3Mn合金熱加工圖研究[J]. 精密成形工程, 2024, 16(2): 10-19.

DAI Lili, ZHOU Jingyi, JING Xuerui, et al. Processing Maps of Mg-3Al-3Sn-0.3Mn Alloy Based on the Strain-compensated Arrhenius Model[J]. Journal of Netshape Forming Engineering, 2024, 16(2): 10-19.

（Corresponding author）