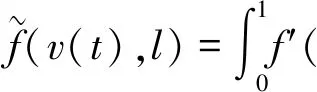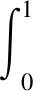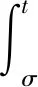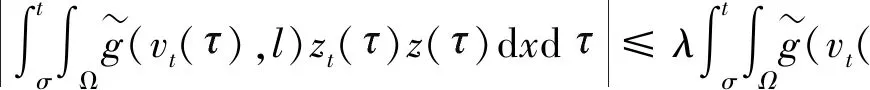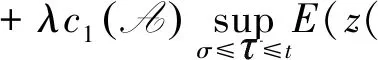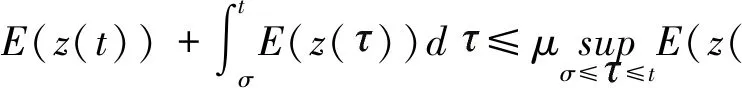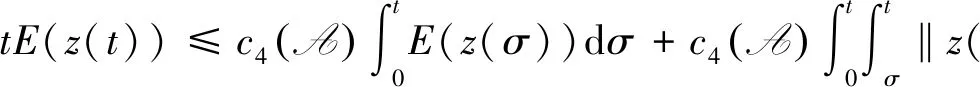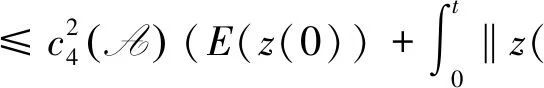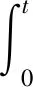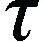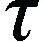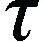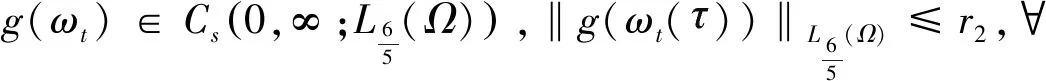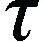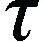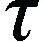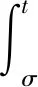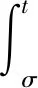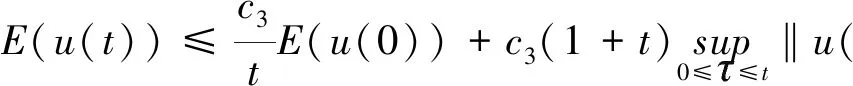具臨界指數的非線性阻尼梁方程的全局吸引子

王思博,姜金平,王雪

(延安大學數學與計算機科學學院, 陜西 延安 716000)

0 引言

設Ω?3,我們考慮方程:

(1)

其中,h∈L2(Ω),g(ωt)為非線性阻尼項,f(ω)為非線性函數,α>0是粘性阻尼系數。

基于以上研究,文獻[4-6]中研究了非線性梁方程的全局吸引子,馬巧珍等[7-8]研究了基爾霍夫型梁方程的全局吸引子和具有記憶項的拉回吸引子,同時蘇小虎,姜金平[9]討論了時間依賴全局吸引子的存在性,但是目前研究具有臨界指數的全局吸引子文獻相對較少,孟鳳娟,曹鳳雪[10]研究了具臨界指數的波方程的時間依賴全局吸引子。本文中討論具臨界指數的非線性阻尼梁方程的全局吸引子。利用文獻[11-13]中的思想,證明了在條件式(2)～(5)下問題(1)的全局吸引子的存在性,并改進了文獻[4]中的結果。此外,在附加條件式(30)下我們證明了全局吸引子的正則性和有限分形維數,并改進了之前的結果。

1 預備知識

我們令H=L2(Ω),在H中的內積和范數分別用〈·,·〉和‖·‖來表示.我們也用‖·‖1來表示在下面H1中的范數。

非線性項f和g滿足下列條件

f∈C1(),|f′(s)|≤c(1+|s|2)

(2)

(3)

g∈C1(),g(0)=0,g是嚴格單調遞增的。

(4)

|g(s)|≤c(1+|s|5)

(5)

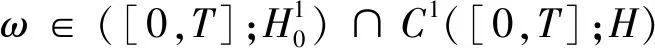
ii)對于所有t∈[0,T],αΔ2ω+g(ωt)∈H;

iii)對于所有t∈[0,T],且x∈Ω使得方程(1)成立,

則ω稱為問題(1)在[0,T]×Ω上的強解。

則稱ω為問題(1)在[0,T]×Ω上的廣義(弱)解。

關于問題(1)解的適定性在文獻[14]中已經得到證明,這里不再進行論證。

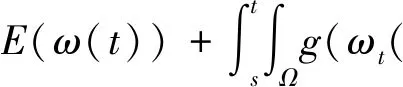
(6)

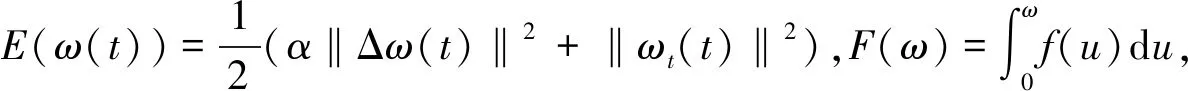
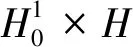
2 全局吸引子

定義2.1[15]設{S(t)}t≥0是度量空間(X,d)上的半群.一個最小的,非空的有界閉集A?X滿足:

對于每一個有界集合B?X,稱為{S(t)}t≥0的全局吸引子。

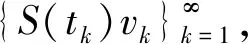
在(6)式中考慮條件(2)～(5),我們可以給問題(1)插入一個不遞增的李亞普諾夫函數

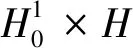
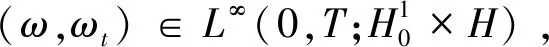
F(ω)∈C([0,T];L1(Ω)),

并且

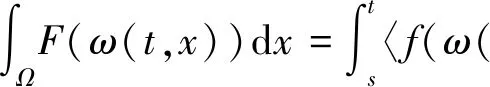
(7)

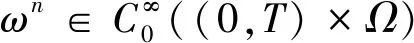
則有

在空間L1((0,T)×Ω)上F(ωn)→F(ω)強收斂;

則(2.1)式成立。

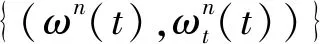
(8)

(9)

則由緊嵌入定理可得

在空間C([s,T];H)中,ωn→ω強收斂

(10)

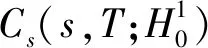
則根據嵌入定理可得在空間L1(Ω)中F(ωn(t))→F(ω(t))強收斂,?t∈[s,T]。

由引理2.1可得

=0.

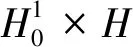
(11)

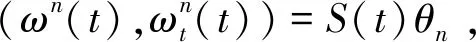
(12)

(13)

(14)

≤E(ωn(s)-ωm(s))

(15)

則

由文獻[13]可知?δ>0,?c2(δ)>0,使得

|u-v|2≤δ+c2(δ)(g(u)-g(v))(u-v)?u,v∈R。

通過以上兩個不等式,我們有

(16)

對于每個δ>0,將下式

兩邊同時乘以ωn-ωm,然后在[0,T]×Ω上積分,并且根據式(13)可得

(17)

由式(16)和式(17)可得

對式(15)關于s在[0.T]上積分,并根據上面的不等式可得

(18)

則由引理2.2可得

(19)

另一方面,由于

由文獻[18,定理5.1],可得

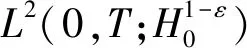
則有

(20)

現在對K4進行估計,使用H?lder不等式有

(21)

利用文獻[12]相似的技巧,通過式(5)和式(12)可以得出

+TmesΩ(|g(-δ)|+|g(δ)|)

(22)

由式(21)～(22)可得

(23)

因此由式(18)～(20)和式(23)可得

則

又因為g∈C()且g(0)=0,則不等式(11)成立。

下面證明半群{S(t)}t≥0的漸近緊性。

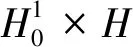
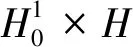
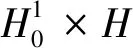
3 吸引子的正則性和有限維數

根據文獻[19]可得,A是不變的,對于每一個φ∈A存在一個不變的軌跡γ={W(t),t∈R}?A,使得

W(0)=φ

(24)

其中不變的軌跡是指連續曲線γ={W(t),t∈R},這使得

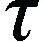
證明全局吸引子A的正則性和有限維數,需要以下引理:

引理3.1假設K是H1上的一個相對緊的子集,并且f(·)滿足條件(2),則對于任意的ε>0,存在δ>0,使得‖u2-u1‖1<δ,

‖f′(u2)-f′(u1)‖L3(Ω)≤ε,?u2,u1∈K

(25)

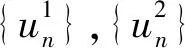
(26)

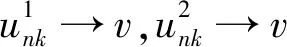
則有

(27)

另一方面,由式(26)和式(2)可以推出:

則式(27)成立。

=0.

與式(26)中第3個關系式矛盾,引理3.1得證。

引理3.2假設K是H1的一個相對緊的子集,并且f(·)滿足條件(2),那么對于?ε>0,?c(ε)>0,使得

‖f′(v)u‖≤ε‖u‖1+c(ε)‖u‖,?v∈K,?u∈H1

(28)

對于每一個v∈K,利用引理3.1,可得

則有

(29)

所以

再由式(29)可得式(28)成立。

下面證明全局吸引子的正則性。

定理3.1令條件式(2)～(5)成立,假設

(30)

則?R>0,使得

‖φ1‖1+‖φ2‖1+‖Δφ1+g(φ2)‖≤R,φ=(φ1,φ2)∈A.

定理3.1的證明設φ=(φ1,φ2)∈A且γ={W(t),t∈R}?A是一個滿足式(24)的不變軌跡,由不變軌跡的定義可以得出

W(·)=(ω(·),ωt(·)),

(ω(t+s),ωt(t+s))=S(t)(ω(s),ωt(s)),?t≥0,?s∈R.

那么v(t)=ω(t+s)是下面問題式(31)的解,

(31)

設s<0,且0

(32)

則

z0=ω(s+l)-ω(s),z1=ωt(s+l)-ωt(s).

將式(32)第一個式子兩邊同時乘以zt和z,并且在(σ,t)×Ω上積分可得:

(33)

(34)

另一方面,由式(30)可得

與(33)式聯立可得

(35)

(36)

由式(33)～(36)可得

(37)

其中0≤σ≤t。

對于μ∈(0,1),我們用強解來證明它,因為式(37)是式(31)的強解,所以作為廣義解也是正確的,因為它們可以用一系列強解來逼近。

(38)

選擇足夠小的ε,結合式(37)和式(38)可得

(39)

在式(39)上關于σ在[0,t]上積分,可得

(40)

另一方面,由于(ω(s),ωt(s))∈A,?s∈R,由式(6)和式(30)可得

則

將上面的不等式代入式(40)可得

tE(z(t))≤cE(z(0))+cl2(1+t),?t≥0

(41)

當s→-∞時,有

(42)

由不等式(42)與ωt∈C([0,∞];H)可得

(43)

并因此有

(44)

(45)

其中,r3與ω(t)無關,在式(31)的第一個式子下,利用式(43)～(45)可得

(46)

其中,r4與ω(t)無關,因此,對于每一個φ=(φ1,φ2)∈A,有

‖φ1‖1+‖φ2‖1+‖Δφ1+g(φ2)‖≤R.

其中R不依賴于φ.

下面證明A的有限維數.

定理3.2假設滿足定理3.1中條件式(30),那么全局吸引子A的分形維數是有限的.

定理3.2的證明設φ1=(ω0,ω1)∈A,φ2=(v0,v1)∈A,(ω,ωt)=S(t)φ1,(v,vt)=S(t)φ2,并且令u=ω-v,則u(t,x)是下面問題的解

(47)

給式(47)第一個式子兩邊同時乘以ut和u,并且在(σ,t)×Ω上積分可得

(48)

則

(49)

在定理3.1中提到,我們可以利用稠密性來證明式(48)和式(49),利用Gronwall引理,從式(48)中可得

(50)

其中,常數c1和ω依賴于A,但是不依賴于φi(i=1,2)。

另一方面,利用式(48)～(49)和引理3.2,并且運用定理3.1中的論證,可得

對于上述不等式關于s在[0,t]上積分可得

(51)

其中,c3依賴于A,但不依賴于φi(i=1,2)。

因此,根據文獻[11,定理3.11]和式(50)～(51)可以得出A的分形維數是有限的。