《函數y=Asin(ωx+φ)》課件設計

夏曉丹

特色與亮點

①課件中插入視頻直觀呈現筒車運動的現實情境，有利于引導學生用數學的眼光看現實世界。

②課件中插入繪制好的幾何圖形，學生通過觀察分析、對比總結，將勻速圓周運動中的物理關系“翻譯”成幾何關系，并獲得函數關系，培養了學生用數學的語言描述現實世界。

③課件中通過超鏈接，直接呈現制作好的各參數對函數y=Asin（ωx+φ）圖象影響的動畫，通過追蹤點的軌跡繪制函數y=Asin（ωx+φ）的圖象，將現實的關系用幾何的方法直觀動態地呈現，使得本課件生動有趣、圖象變換動態直觀；利用幾何畫板軟件繪制函數y=Asin（ωx+φ）圖象不僅使“畫圖象”變得簡單，而且使“參數φ，ω，A的變化”引起相關對象的運動變化也有了更直觀的呈現，有助于理解其內在的邏輯關系。

制作背景

本節課是典型的數學模型探索課程，學生需要從現實問題中抽象概括出數學模型，對該數學模型的圖象與性質進行研究，并利用該數學模型解決問題。為了實現較好的課堂教學效果，引導學生學會用數學的眼光看現實世界，學會用數學的語言描述現實世界，并培養學生的數學建模素養，本課件通過視頻展示、動畫演示，引導學生經歷數學建模的全過程，通過自己動手實驗，真正體會數學模型是如何建立的。

本課件的制作實現了生活現象數學化，學生可以通過觀察視頻、動畫，發現數學中的三角函數、物理中的勻速圓周運動以及現實中的筒車運動之間的內在的聯系。課件從筒車運動的實際問題出發，讓學生體會從已知出發去探索未知、從特殊到一般進行提問的研究思路，滲透了數學源于生活的本質。

設計思路及內容結構

1.設計思路

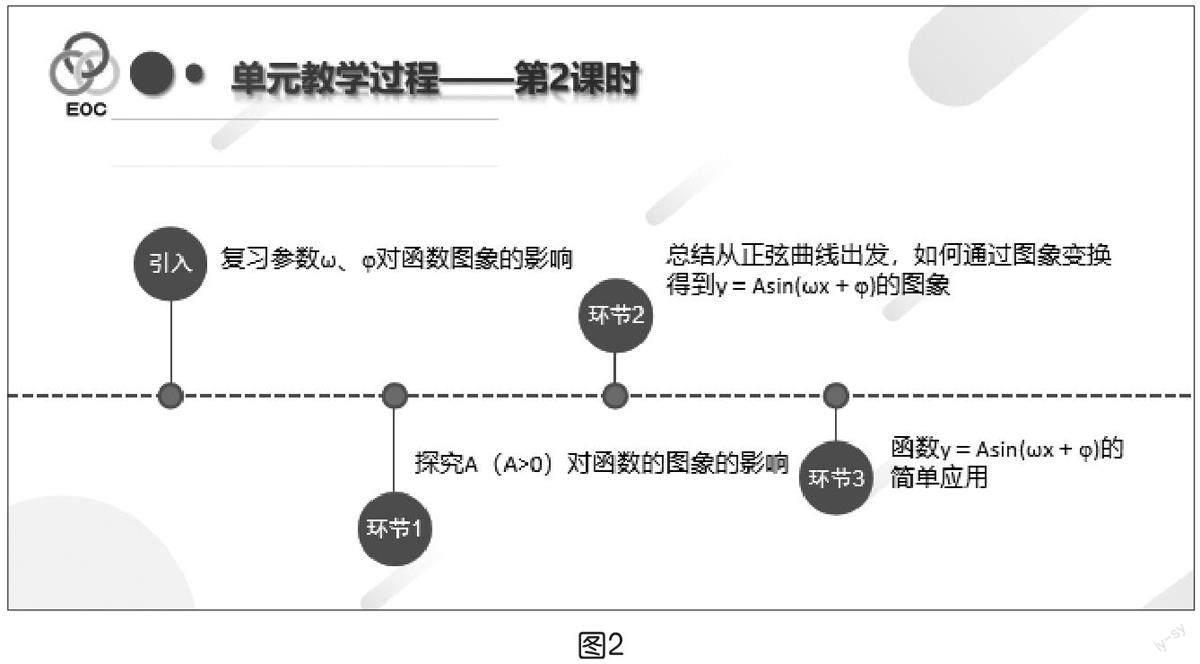
本單元選自人教A版（2019）第五章第6節，建議用2課時完成。第1課時（如圖1），經歷對筒車運動的數學建模過程，提出對數學函數y=Asin（ωx+φ）的研究思路，探究參數φ，ω對函數y=Asin（ωx+φ）的影響。第2課時（如下頁圖2），在第1課時的基礎上，繼續研究參數A對函數y=Asin（ωx+φ）的影響，并歸納總結出從正弦函數圖象出發，通過圖象變換得到函數y=Asin（ωx+φ）（A>0，ω>0）圖象的過程與方法；會用“五點法”和圖象變換的方法畫函數y=Asin（ωx+φ）的簡圖，并能應用函數y=Asin（ωx+φ）的圖象與性質解決簡單的實際問題。

借助筒車這一現實模型，說明函數y=Asin（ωx+φ）與現實中的勻速圓周運動之間的內在聯系；通過對筒車運動變化規律的觀察分析、抽象概括，獲得函數模型y=Asin（ωx+φ），能說出參數φ，ω，A以及變量x，y的物理意義，進一步體會三角函數與現實世界的密切聯系，發展數學建模素養。

借助幾何畫板軟件，通過數學實驗，經歷平移變換和伸縮變換獲得函數y=Asin（ωx+φ）的圖象，掌握參數φ，ω，A對函數圖象的影響，理解參數φ，ω，A在圓周運動中的實際意義，發展數學抽象、邏輯推理與直觀想象的素養。

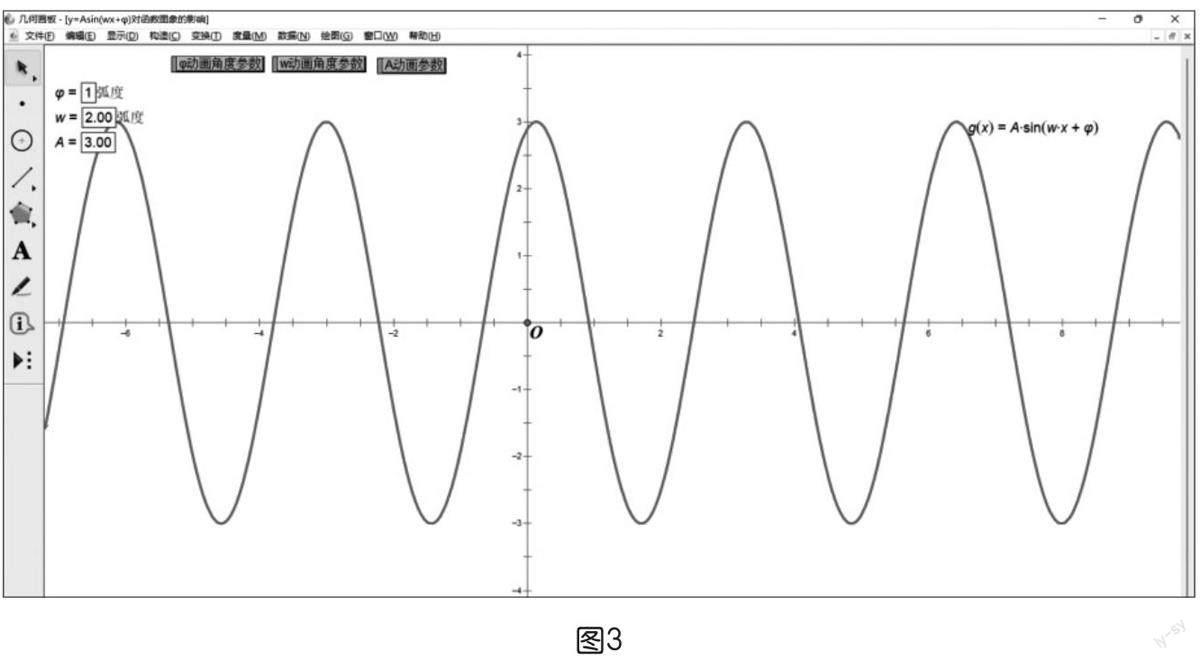
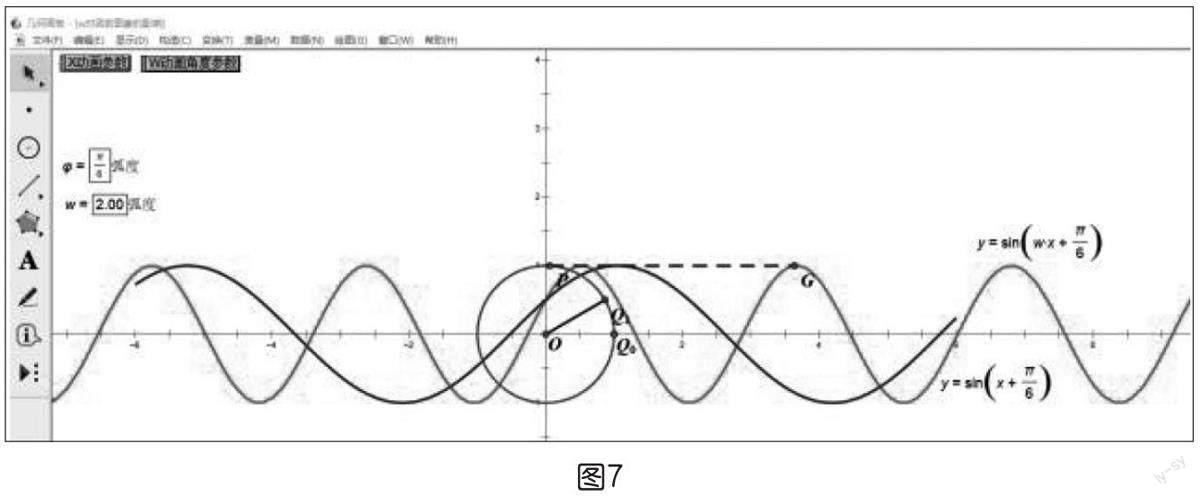
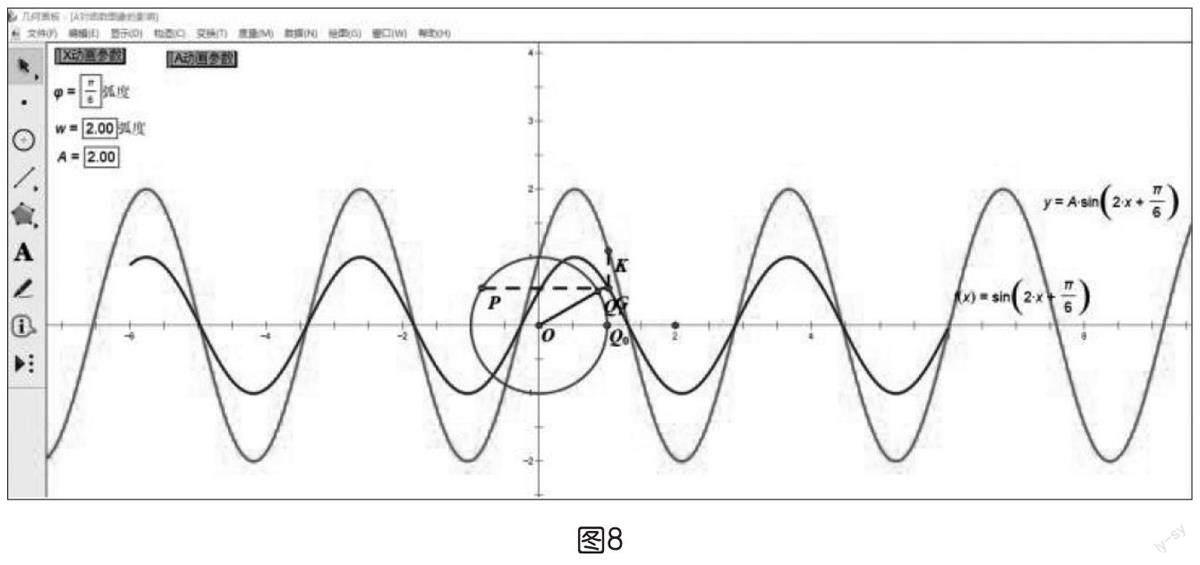
在研究參數φ，ω，A對函數y=Asin（ωx+φ）圖象的影響時，參數多，解析式、圖象中的各要素之間的關系比較復雜，相互關聯比較隱蔽，準確作圖也比較困難。課件中利用幾何畫板（如圖3）快速準確地畫圖，直觀呈現各參數對函數圖象的影響，引導學生在觀察發現的基礎上進行理性思考，得出一般結論，進而突破教學難點。

2.內容結構

（1）環節1：創設問題情境，提出研究問題

課件中插入視頻（如圖4）呈現筒車運動過程實景，引導學生將其抽象成質點的勻速圓周運動，滲透數學源于生活的本質，引出本課的核心內容。

（2）環節2：抽象簡化問題，建立函數模型

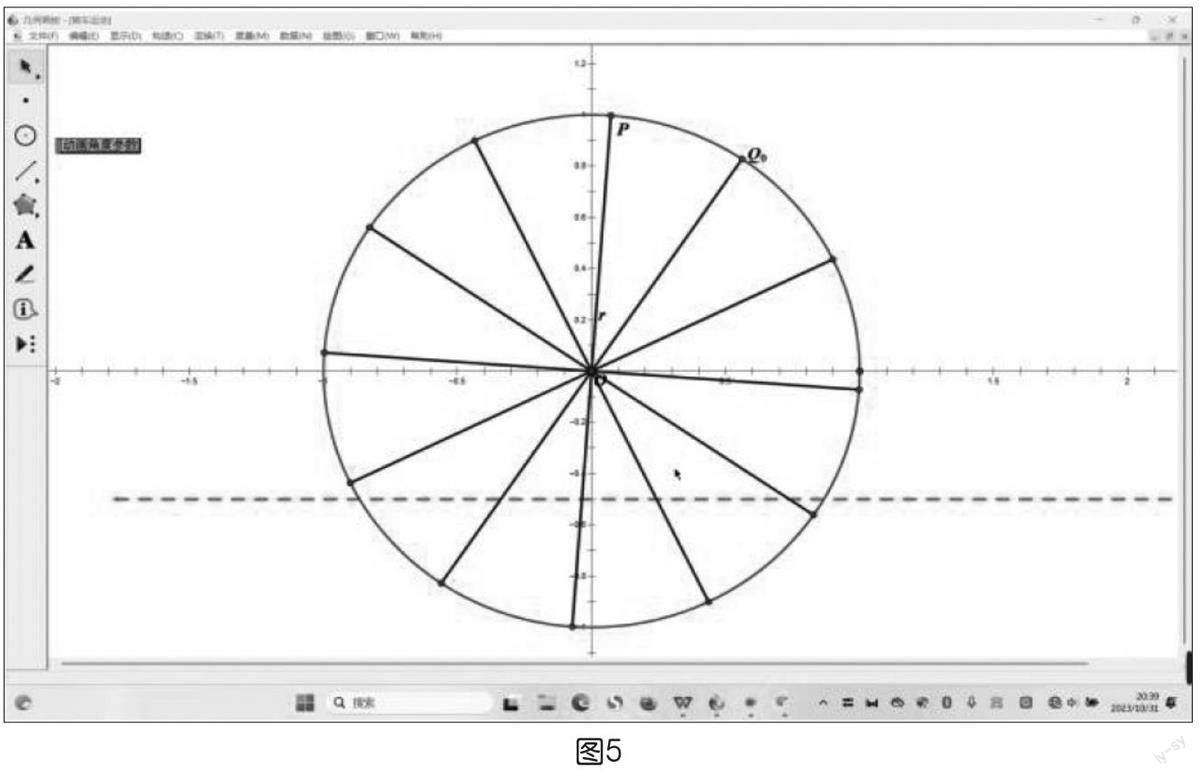
課件通過幾何畫板制作筒車運動動畫（如下頁圖5），將筒車運動抽象成質點的勻速圓周運動，觀察運動中的相關要素，抽象出其中的幾何對象與幾何關系，引導學生分析其中的變量和常量，尋找盛水筒距離水面的相對高度與時間的關系，從而突破數學建模這一難點。

結合筒車的圓周運動研究函數y=Asin（ωx+φ），不僅能聯系實際，突出參數φ，ω，A的物理意義，而且能夠聯系函數解析式、函數圖象，并充分揭示它們之間的內在邏輯關系，為提升學生數學抽象、直觀想象和邏輯推理等數學素養提供重要平臺。

（3）環節3：探究φ，ω，A對函數圖象的影響

課件中取參數的初始值A=1，ω=1，φ=0，此時動點在單位圓上從點Q出發以單位速度轉動，經

通過一定量的積累后，學生形成圖象伸縮變換的感性認識，再進一步從物理角度、幾何關系、函數關系、點的坐標關系等角度進行分析，在此基礎上，得到參數ω對

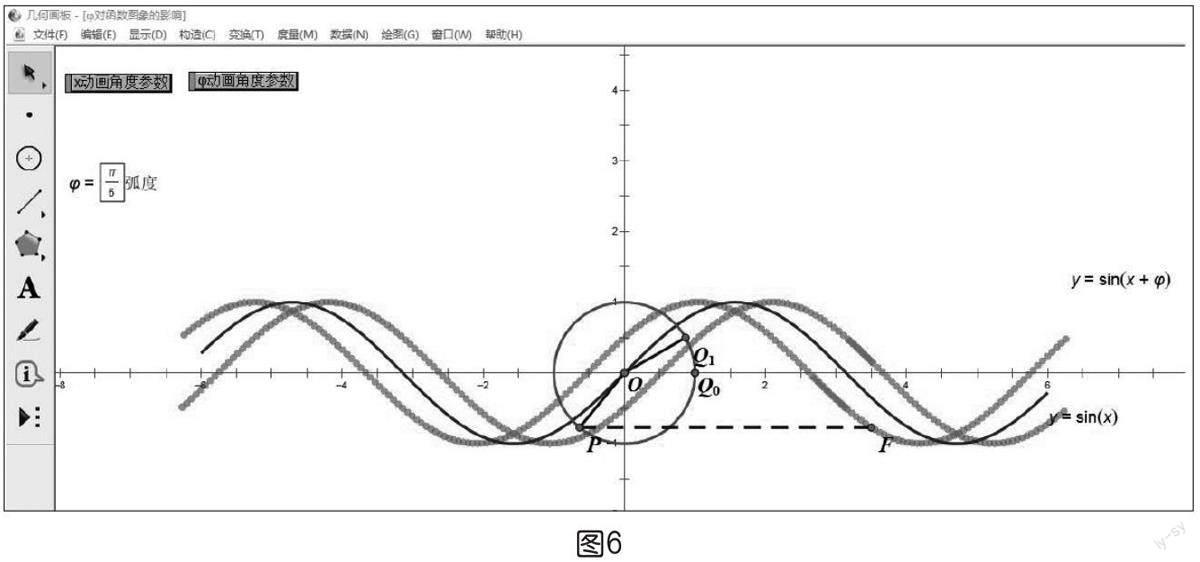
在針對函數y=Asin（ωx+φ）的研究過程中，通過一連串的“思考”與“探究”，引導學生觀察、分析、歸納、概括、抽象、聯想、綜合、總結。由于參數φ的變化涉及函數圖象的平移變換，學生已有一定的學習經驗，建議首先研究；參數ω的變化涉及函數圖象的伸縮變換，是學習的難點，需要重點突破；有前面學習內容做鋪墊，對參數A對函數圖象的影響學生能夠自主研究完成。每一個參數的探索都要遵循從特殊到一般、從具體到抽象的研究思路，一方面結合筒車運動模型解釋各參數的實際意義，另一方面從相應函數圖象上點的坐標變化看圖象的變換，真正理解圖象變換的本質。

（4）環節4：畫函數y=Asin（ωx+φ）的圖象

通過以上的數學實驗探究，學生了解了參數φ，ω，A對函數y=Asin（ωx+φ）圖象的影響。通過“思考”要求學生總結、提煉出圖象變換規律，進而說明由正弦函數圖象，經過平移變換、橫坐標的伸縮變換（周期變換）、縱坐標的伸縮變換（振幅變換）三種圖象變換得到函數y=Asin（ωx+φ）的圖象的過程與方法：從正弦曲線出發，先進行相位變換，再進行周期變換，然后進行振幅變換。

通過課件引導學生從局部的討論過渡到整體的思考，從特殊的例子歸納概括出一般性的結論，得到從正弦函數的圖象出發，通過圖象變換得到y＝Asin（ωx+φ）圖象的過程與方法，并提醒學生注意比較不同變換順序之間的差異。同時，引出“五點法”作圖，并從兩種方法的聯系上來加深學生對y＝Asin（ωx+φ）圖象的認識。

（5）環節5：小結

出示以下問題：①概述本單元知識的基本脈絡。②如何理解函數y=Asin（ωx+φ）中參數φ，ω，A的物理意義？說明各參數對函數y=Asin（ωx+φ）圖象的影響。③如何由正弦曲線通過圖象變換得到函數y=Asin（ωx+φ）的圖象？④在研究函數y=Asin（ωx+φ）圖象的過程中，哪些思想方法值得總結？

關鍵技術處理

①使用幾何畫板軟件制作筒車運動動畫和各參數對函數y=sin（ωx+φ）圖象的影響動畫，需要使用幾何畫板軟件的功能包括繪制圖形、繪制點、定義新參數、創建新參數動畫、建立動畫操作臺、構造新函數、繪制函數圖象、追蹤點的軌跡、隱藏函數圖象、隱藏點等。

②使用PPT中的屏幕錄制功能錄制筒車運動模型的動畫；采用超鏈接的呈現動畫，即點擊鏈接就可以打開制作好的動畫GSP文件。想要打開動畫GSP文件可以將GSP5chs程序拷貝到U盤里，打開方式是先找到U盤，再找到GSP5chs程序即可。還可以將GSP5chs程序拖拽到計算機桌面，打開方式是先找到桌面，再找到GSP5chs程序即可。

③使用花瓣剪輯軟件對視頻、動畫進行后期剪輯。

幕前幕后

在制作本課件前筆者提前制作筒車運動模型的動畫、參數φ，ω，A分別對函數y=Asin（ωx+φ）圖象影響的動畫、函數y=Asin（ωx+φ）圖象變化的動畫。通過本課件的制作，筆者對數學實驗軟件使用的能力有了很大的提高，接下來筆者會繼續學習多媒體課件制作的相關知識，并將信息技術應用到合適的課堂教學中。