考慮AGV運輸和機器轉(zhuǎn)速的作業(yè)車間綠色調(diào)度研究*
李崢峰,張東方,丁其聰,張國輝
(1.中原工學(xué)院 機電學(xué)院,河南 鄭州 450007;2.鄭州航空工業(yè)管理學(xué)院 管理工程學(xué)院,河南 鄭州 450015)
0 引 言
在制造車間中,機器被用于切削加工的時間在整個生產(chǎn)過程中所占比例較低,大部分時間被浪費在非加工過程。有研究表明,零件加工以外的時間能占到整個生產(chǎn)過程的95%,其中工件的運輸時間更是占了大部分[1],因此在車間生產(chǎn)過程中,運輸過程不可忽略。同時,自動導(dǎo)引車(automated guided vehicle, AGV)逐漸成為車間生產(chǎn)中常用的運輸工具,在車間中得到了廣泛應(yīng)用。
隨著我國制造業(yè)的迅速發(fā)展,能源的消耗量也在與日俱增。研究表明,機器的待機能耗在整個加工過程中占比較高,以加工中心為例,非加工過程能量消耗占比高達(dá)40%以上[2-3]。此外,工件運輸過程中,AGV的能量消耗也不可忽略。車間生產(chǎn)調(diào)度作為智能制造系統(tǒng)的重要環(huán)節(jié),其通過合理調(diào)度各類資源,以達(dá)到提高生產(chǎn)效率、節(jié)約成本、降低能耗的目的。
作業(yè)車間調(diào)度是一種常見的車間生產(chǎn)調(diào)度問題,開展針對作業(yè)車間綠色調(diào)度問題的研究具有重要意義。
在車間各種能耗中,由于機器能耗占據(jù)車間總能耗的比重較大,因此,近年來國內(nèi)外有學(xué)者從優(yōu)化機器能耗的角度對車間綠色調(diào)度問題進(jìn)行了研究。整體來看,目前對于車間綠色調(diào)度問題中優(yōu)化機器能耗的研究,主要從兩個大的方面進(jìn)行:1)設(shè)置機器關(guān)機/重啟的車間綠色調(diào)度;2)調(diào)整機器轉(zhuǎn)速的車間綠色調(diào)度。
對于設(shè)置機器關(guān)機/重啟的車間綠色調(diào)度,能夠使閑置等待時間較長的機器及時關(guān)機,節(jié)省能耗。然而,機器頻繁地關(guān)機/重啟,不僅對機器閑置等待的時長有要求,而且還會影響機器的使用壽命。而通過調(diào)整機器轉(zhuǎn)速則可以避免這些問題的產(chǎn)生,并且機器轉(zhuǎn)速的改變不僅影響工序的實際加工時間,對相應(yīng)工序的機器能耗也將產(chǎn)生較大影響。因此,對考慮機器轉(zhuǎn)速的車間綠色調(diào)度問題的研究逐漸引起了學(xué)者的關(guān)注。
ZHU H等人[4]采用多目標(biāo)離散水波優(yōu)化算法(multi-objective discrete water wave optimization,MODWWO)研究了機器加工速度可變的多目標(biāo)作業(yè)車間綠色調(diào)度問題。WU X等人[5]研究了考慮機器加工速度的流水車間綠色調(diào)度問題。GAO Z等人[6]采用改進(jìn)蛙跳算法研究了機器加工速度可變的混合流水車間綠色調(diào)度問題。張國輝等人[7]采用改進(jìn)遺傳算法求解了考慮機器速度的柔性作業(yè)車間綠色調(diào)度問題。吳秀麗等人[8]采用帶精英策略的非支配排序遺傳算法II(non-dominated sorting genetic algorithm-II,NSGA-II),求解了考慮機器轉(zhuǎn)速的柔性作業(yè)車間綠色調(diào)度問題。
綜上所述,目前對于調(diào)整機器轉(zhuǎn)速的車間綠色調(diào)度問題的研究還不是很豐富,并且一些研究者為了便于求解,對模型進(jìn)行了簡化,忽略了工件在加工機器之間運輸?shù)倪^程。這顯然是不合理的,特別是當(dāng)機器之間的距離較遠(yuǎn)、運輸時間較長時,運輸過程更不可忽略。
AGV在車間的廣泛應(yīng)用,減輕了工人的勞動強度,提高了車間生產(chǎn)的智能化程度。同時AGV的引入也帶來了AGV的任務(wù)分配問題,使問題的求解更加復(fù)雜,引起了廣大研究者的關(guān)注。
XU Y等人[9]采用改進(jìn)粒子群優(yōu)化算法研究了考慮AGV運輸?shù)娜嵝宰鳂I(yè)車間調(diào)度問題。HAI Y M等人[10]研究了作業(yè)車間AGV與機器雙資源集成調(diào)度問題,并通過實驗對AGV與機器雙資源集成調(diào)度策略的有效性進(jìn)行了驗證。LIU Q等人[11]研究了考慮AGV運輸?shù)娜嵝宰鳂I(yè)車間雙資源集成調(diào)度問題,并采用改進(jìn)遺傳算法對完工時間進(jìn)行了優(yōu)化。馬千惠等人[12]采用改進(jìn)NSGA-II算法,研究了AGV和機器雙約束的柔性作業(yè)車間多目標(biāo)優(yōu)化問題。周鑫[13]在考慮AGV運輸?shù)幕A(chǔ)上,采用改進(jìn)遺傳算法研究了柔性作業(yè)車間調(diào)度問題,并實現(xiàn)了對完工時間的優(yōu)化目的。
綜合以上文獻(xiàn)可知,盡管已有學(xué)者研究了考慮AGV運輸?shù)能囬g調(diào)度問題,并取得了一定成果,但是從綠色調(diào)度的角度研究考慮AGV運輸?shù)能囬g調(diào)度問題的文獻(xiàn)較少,特別是考慮AGV運輸和機器轉(zhuǎn)速的車間綠色調(diào)度問題的研究,幾乎沒有相關(guān)文獻(xiàn)。在車間實際生產(chǎn)過程中,機器轉(zhuǎn)速的改變會影響工序的完工時間和相應(yīng)的機器能耗。通常來說,工序在機器上加工時,機器轉(zhuǎn)速越高,完工時間越小,但相應(yīng)的機器能耗越高。此外,隨著企業(yè)對準(zhǔn)時化交貨期要求的不斷提高,車間對工件運輸準(zhǔn)時性的要求也不斷提高。如果只考慮加工過程而忽視運輸過程,則會導(dǎo)致工件無法按時運送到相應(yīng)機器上,影響生產(chǎn)進(jìn)度。
基于此,筆者以作業(yè)車間為研究對象,對考慮AGV運輸和機器轉(zhuǎn)速的作業(yè)車間綠色調(diào)度問題展開研究。
由于最大完工時間Cmax和總能耗E這兩個指標(biāo)存在沖突關(guān)系,且最大完工時間Cmax在企業(yè)中占據(jù)主導(dǎo)地位,此外最大完工時間的減少也側(cè)面反映了車間公共系統(tǒng)能耗和機器空載能耗的減少,縮短最大完工時間在一定程度上減少了車間總能耗。基于此,筆者采用兩階段優(yōu)化的方式分別對最大完工時間和總能耗進(jìn)行優(yōu)化。
第一階段,機器以最高轉(zhuǎn)速進(jìn)行加工,采用改進(jìn)的麻雀搜索算法(sparrow search algorithm, SSA)優(yōu)化車間最大完工時間;第二階段,在保證第一階段優(yōu)化得到的最大完工時間最小值不變的前提下,提出一種間隙檔位調(diào)整策略(gap gear adjustment strategy,GGAS),通過降低部分工序的機器轉(zhuǎn)速來降低能源消耗,實現(xiàn)對總能耗的優(yōu)化;最后,通過實驗對改進(jìn)麻雀搜索算法的有效性進(jìn)行了驗證,并對算法改進(jìn)策略及間隙檔位調(diào)整策略的有效性進(jìn)行了驗證。
1 考慮AGV運輸和機器轉(zhuǎn)速的車間調(diào)度問題
1.1 問題描述
考慮AGV運輸和機器轉(zhuǎn)速的作業(yè)車間綠色調(diào)度問題描述如下:有n個工件在m臺機器上加工,每個工件i包含hi道工序,每臺機器有d個檔位,且不同的檔位對應(yīng)不同的轉(zhuǎn)速和功率;每道工件工序Oij所在的加工機器已知,且可以使用該機器的所有檔位,同時有r輛AGV小車負(fù)責(zé)把工件運輸?shù)较鄳?yīng)的機器上進(jìn)行加工;機器分為加工狀態(tài)和空載狀態(tài),兩種狀態(tài)的功率不同;AGV分為負(fù)載運輸和空載運輸,兩種運輸?shù)墓β室膊煌?/p>
此外,該問題還需要滿足以下假設(shè)條件:
1)在0時刻,所有機器、工件與AGV均已準(zhǔn)備就緒;
2)機器的檔位一旦確定,在加工過程中不允許改變;
3)同一機器以不同的檔位進(jìn)行加工時,加工時間和機器的能耗也不同;
4)機器間存在無限大的緩沖區(qū);
5)所有AGV和工件的初始位置均在裝載區(qū)M0,最終位置均在卸載區(qū)Mm+1;
6)AGV完成運輸任務(wù)后停靠在機器旁,等待下一次運輸任務(wù);
7)AGV小車空載和負(fù)載速度相同;
8)任一時刻,一臺AGV只能運輸一個工件,一個工件也只能被一臺AGV運輸;
9)AGV電量充足;
10)工件的裝卸時間包含在加工時間中;
11)每個工件必須在前一道工序加工完畢后才可運輸至下一臺機器上進(jìn)行加工。
1.2 兩階段目標(biāo)函數(shù)及調(diào)度模型
筆者采用兩階段優(yōu)化的方式依次對最大完工時間Cmax和總能耗E進(jìn)行優(yōu)化。第一階段,采用改進(jìn)的麻雀搜索算法優(yōu)化企業(yè)最重要的指標(biāo)Cmax;第二階段,在保證第一階段優(yōu)化得到的Cmax最小值不變的基礎(chǔ)上,采用間隙檔位調(diào)整策略,對E進(jìn)行優(yōu)化。
兩階段優(yōu)化的目標(biāo)函數(shù)如下:
1)最大完工時間最小。其表達(dá)式如下:
minCmax=min(maxCij)
(1)
式中:Cmax為最大完工時間;i為工件編號;j為工序編號;Cij為工件i的j工序的完工時間。
2)車間總能耗最小。車間的總能耗包括機器加工能耗E1、機器空載能耗E2、AGV運輸能耗E3和車間公共系統(tǒng)的能耗E4四部分。
①機器加工能耗E1。其由加工功率和加工時間的乘積表示如下:
(2)
式中:n為工件數(shù)量;j為工序編號;hi為工件i的工序數(shù);Mij為工序Oij的加工設(shè)備;q為機器的檔位編號,q∈{1,2,…,d};d為機器的檔位數(shù);PMijq為工序Oij在機器Mij以檔位q加工時的功率;TijMijq為工序Oij在機器Mij上以檔位q加工的加工時間;YMijq為機器Mij是否以檔位q加工的工件,若是則YMijq=1,否則YMijq=0;
②機器的空載能耗E2。其由機器空載功率和機器前后兩道相鄰工序之間存在的加工間隙時長的乘積表示如下:
(3)

③AGV運輸能耗E3。其包括負(fù)載運輸階段能耗和空載運輸階段能耗,可表示如下:

(4)
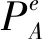
④車間公共系統(tǒng)能耗E4。車間的照明、通風(fēng)等的能耗,由公共系統(tǒng)功率和最大完工時間的乘積表示如下:
E4=P0Cmax
(5)
式中:P0為車間公共系統(tǒng)功率。
因此,車間總能耗E為:
E=E1+E2+E3+E4
(6)
AGV負(fù)載運輸開始時間受AGV可用時刻、AGV從當(dāng)前位置到工件上道工序加工機器的時間和工件上道工序完工時間的約束。
其約束公式如下:
Al-start=max{Al-able+Tl-pos-Mi(j-1),Ci(j-1)}
(7)
式中:Al-start為AGV小車Al負(fù)載運輸工件的開始時刻;Al-able為AGV小車Al可用時刻;Ci(j-1)為工序Oi(j-1)完工時間。
AGV負(fù)載運輸完成時間約束公式如下:
Al-end=Al-start+Tl-mi(j-1)-Mij
(8)
式中:Al-end為AGV小車Al負(fù)載運輸工序Oi(j-1)到下一道工序Oij加工機器的完成時刻。
工序Oij在機器Mij上的開始加工時間受AGV可用時刻、AGV從當(dāng)前位置到機器Mi(j-1)時間、AGV從工件上道工序所在機器Mi(j-1)到機器Mij的時間、工件上道工序完工時間、機器Mij上一道工序Oi′j′完工時間的約束。其約束公式如下:
閱讀作為獲得語言知識的基本途徑,其形式是不拘一格的,所以筆者在教學(xué)中鼓勵學(xué)生,只要用心閱讀,不管采用什么形式的閱讀都是對學(xué)習(xí)有利而無害的。筆者結(jié)合高職學(xué)生學(xué)習(xí)英語的狀況,致力于嘗試將圖式理論運用到英語閱讀教學(xué)中,它是指閱讀者對所讀的內(nèi)容、內(nèi)容主旨、內(nèi)容了解程度和熟悉程度的總稱,將之運用到英語閱讀教學(xué)中取得了一定的教學(xué)效果。
SijMijq=max{Al-able+Tl-pos-Mi(j-1)+Tl-Mi(j-1)-Mij,
Ci(j-1)Mi(j-1)q+Tl-Mi(j-1)-Mij,Ci′j′Mijq′}
(9)
工序Oij的完工時間約束公式如下:
CijMijq=SijMijq+TijMijq
(10)
式中:CijMijq為工序Oij在機器Mij上以檔位q加工的結(jié)束時間。
同一工件的工序間有加工先后約束關(guān)系,其約束公式如下:
Ci(j+1)Mi(j+1)q-CijMijq≥TijMijq
(11)
機器的加工檔位一旦確定,在加工過程中不允許改變,其約束公式如下:
(12)
一道工序只能由一輛AGV進(jìn)行運輸,其約束公式如下:
(13)
2 改進(jìn)麻雀搜索算法求解
麻雀搜索算法是由XUE J等人[14]于2020年提出的一種新型群智能優(yōu)化算法,其具有參數(shù)設(shè)置簡單、尋優(yōu)能力強和易于實現(xiàn)等優(yōu)點,在解決優(yōu)化問題時具備良好的性能。
麻雀搜索算法根據(jù)麻雀個體分工不同,將種群分為發(fā)現(xiàn)者、加入者。發(fā)現(xiàn)者負(fù)責(zé)為種群尋找食物,指引種群覓食方向;加入者跟隨發(fā)現(xiàn)者進(jìn)行覓食。同時,該方法設(shè)立偵察預(yù)警機制用來躲避危險。
麻雀搜索算法自提出以來已經(jīng)得到了廣泛的應(yīng)用,并在路徑規(guī)劃、電動汽車充電站規(guī)劃、故障診斷和車間調(diào)度等領(lǐng)域已經(jīng)取得了一些研究成果。
2.1 離散化編碼
2.1.1 編碼機制
筆者采用基于工序的編碼方式。由于AGV小車需要在裝載區(qū)、機器和卸載區(qū)之間運輸工件,因此,每個工件的運輸任務(wù)數(shù)比該工件工序數(shù)多1。
為了使工序數(shù)和AGV的運輸任務(wù)數(shù)統(tǒng)一,筆者為每個工件增加一道虛擬工序,并把卸載區(qū)假設(shè)為該虛擬工序的虛擬機器。虛擬工序在虛擬機器上的加工時間為0,工序編碼染色體的長度為總工序數(shù)+總工件數(shù)。
假設(shè)車間有2個工件,第一個工件有2道工序,第二個工件有3道工序,則工序編碼染色體的長度為總工序數(shù)與總工件數(shù)之和7。
其中一個編碼方案如圖1所示。

圖1 工序編碼
圖1中,元素值表示工件號,從左到右元素出現(xiàn)的次數(shù)表示該工件的第幾道工序。比如1表示工件1,其中第一個1表示工件1的第一個工序,第二個1表示工件1的第二道工序。
2.1.2 轉(zhuǎn)換機制
麻雀搜索算法的解是連續(xù)值,而作業(yè)車間調(diào)度問題的解是離散值。為了使麻雀搜索算法適用于作業(yè)車間調(diào)度問題,需要將連續(xù)的解轉(zhuǎn)換為離散的解。針對工序序列,常用的轉(zhuǎn)換規(guī)則有排序順序值(ranked order value, ROV)轉(zhuǎn)換規(guī)則和最大位置值(largest position value, LPV)轉(zhuǎn)換規(guī)則,但這兩種轉(zhuǎn)換規(guī)則只能解決所有工件具有相同工序數(shù)的問題,具有一定的局限性。基于此,筆者設(shè)計一種排列順序轉(zhuǎn)換(sort order conversion, SOC)規(guī)則對工序序列進(jìn)行解空間的轉(zhuǎn)換,不論工件的工序數(shù)量是否相同,該轉(zhuǎn)換規(guī)則都可以實現(xiàn)連續(xù)值到離散工序的轉(zhuǎn)換。
具體操作過程為:首先根據(jù)工件號從小到大的順序,獲取工件號i及其工序數(shù)j,然后按從小到大的順序把相應(yīng)位置j個解轉(zhuǎn)換為工件號i,直到所有工序完成轉(zhuǎn)換,這樣得到了基于工序編碼的離散解,工件號出現(xiàn)的次序就代表其加工工序。
其轉(zhuǎn)換過程如圖2所示。

圖2 SOC工序編碼轉(zhuǎn)換
圖2以兩個工件為例:第一個工件有5道工序,從連續(xù)解A序列中找到5個最小的值,把對應(yīng)位置的B值設(shè)置為1;第二個工件有4道工序,在連續(xù)解A中剩下的序列中找到最小的4個值,把對應(yīng)位置B的值設(shè)置為2,按工件號依次完成所有的工件工序的轉(zhuǎn)換。B中工件號出現(xiàn)的次序就表示該工件的工序。
2.2 解碼
編碼完成后還需要進(jìn)行解碼,才能得到具體的調(diào)度方案。對工序編碼序列從左往右依次解碼,得到相應(yīng)的工序Oij和該工序?qū)?yīng)的機器以及加工時間。由于上述編碼方法僅涉及工序編碼,并未涉及AGV編碼,因此,在解碼時需要考慮AGV的任務(wù)分配問題。
針對AGV任務(wù)分配問題,筆者采用“先到先搬運”的啟發(fā)式規(guī)則進(jìn)行AGV的任務(wù)分配。
具體步驟如下:
1)依次讀取工序編碼序列的每一個基因,轉(zhuǎn)換為相應(yīng)的工序Oij;
2)根據(jù)工序編碼依次獲得每道工序的加工設(shè)備;
3)根據(jù)每道工序的加工設(shè)備依次獲得每道工序?qū)?yīng)的運輸任務(wù),獲得運輸起止點和運輸時間;
4)找出工序Oij前一道工序所在機器Mi(j-1),若j=1,此時工件還在裝載區(qū)M0位置,則Mi(j-1)=M0。根據(jù)AGV當(dāng)前位置和AGV完成本次運輸任務(wù)的結(jié)束時間,在所有AGV中選擇最早到達(dá)Mi(j-1)的AGVl。如果滿足最早到達(dá)條件的AGVl不止一臺,則從中隨機選擇一臺;如果AGVl已經(jīng)在機器Mi(j-1)處,轉(zhuǎn)至6),否者轉(zhuǎn)至5);
5)將AGVl從原來位置移動到機器Mi(j-1);
6)AGVl將工件i從機器Mi(j-1)運輸?shù)綑C器Mij;
7)由式(7)和AGVl運輸時間,更新AGVl可用時刻Al-able和AGVl當(dāng)前位置;
8)是否全面解碼完畢:是跳轉(zhuǎn)9),否跳轉(zhuǎn)1);
9)結(jié)束。
2.3 初始化種群
標(biāo)準(zhǔn)麻雀搜索算法采用隨機初始化方式生成初始種群。隨機初始化雖然簡單易操作,但是也會造成生成的種群個體分布較隨機、種群質(zhì)量不高,影響收斂速度。而反向?qū)W習(xí)策略通過生成當(dāng)前種群個體的反向個體,并對個體進(jìn)行評估,挑選較優(yōu)個體組成新的種群,可以提高種群個體的質(zhì)量,加快收斂速度[15]。
基于此,筆者采用反向?qū)W習(xí)策略生成麻雀初始種群,提高種群質(zhì)量,加快算法收斂速度。
其實現(xiàn)過程為:隨機生成初始種群Xu=[xu1,xu2,…,xuD],u=1,2,…,N。其中:N表示種群規(guī)模,u表示個體,D表示維數(shù)。

(14)
式中:lb,ub為搜索空間的上下界。
將生成的反向種群和原初始種群合并成一個新的種群,并按照適應(yīng)度值對新種群個體進(jìn)行排序,從中挑選出前50%適應(yīng)度較好的個體,將其作為新的麻雀初始種群。
2.4 局部搜索策略
麻雀種群中的發(fā)現(xiàn)者負(fù)責(zé)為種群尋找食物源、提供覓食方向,加入者通過跟隨發(fā)現(xiàn)者來獲取食物。因此,發(fā)現(xiàn)者的位置在很大程度上決定著整個種群能否獲取足夠的食物,有必要對發(fā)現(xiàn)者進(jìn)行深度發(fā)掘,擴大其搜索范圍,進(jìn)行細(xì)致搜索以尋求更優(yōu)位置。而局部搜索能夠通過小的局部變化來改進(jìn)給定的解決方案[16]。
基于此,筆者在發(fā)現(xiàn)者位置更新后提出一種局部搜索策略,對發(fā)現(xiàn)者進(jìn)行深度發(fā)掘以尋求更優(yōu)位置。局部搜索策略具體操作為:在發(fā)現(xiàn)者位置更新后,于當(dāng)前個體位置向量中隨機選擇四個不同的位置,對這四個位置的元素進(jìn)行重新排列產(chǎn)生另外23個可行解,如圖3所示。

圖3 局部搜索策略
位置1、位置2、位置3和位置4共有24種排列方式。對這四個位置的元素進(jìn)行排列可以產(chǎn)生另外23個可行解,選取其中最優(yōu)的個體進(jìn)入下一次迭代。
2.5 模擬退火算法
麻雀搜索算法在迭代后期易陷入局部最優(yōu),而模擬退火算法能夠以一定概率接受比原個體差的新個體,使算法跳出局部最優(yōu)的“陷阱”[17]。筆者在麻雀搜索算法后引入模擬退火算法作用于種群前2%最優(yōu)個體。
模擬退火算法操作如下:
1)初始化參數(shù)設(shè)置;
2)根據(jù)初始解S得到新解S′,比較新解適應(yīng)度值f(S′)和初始解適應(yīng)度值f(S)的大小。如果f(S′) exp(-(f(S′)-f(S))/T) (15) 式中:T為當(dāng)前溫度。 其中:若exp(-(f(S′)-f(S))/T)>ε(ε表示0到1之間的隨機數(shù)),則令S=S′,否者保留當(dāng)前解S; 3)按照降溫公式對當(dāng)前溫度進(jìn)行降溫迭代: T0=T0×rate (16) 式中:T0為初始溫度;rate為降溫速度; 4)判斷當(dāng)前溫度是否小于設(shè)定終止溫度,若是,則結(jié)束,輸出最優(yōu)解,否則跳轉(zhuǎn)步驟2)。 設(shè)定機器有1、2、3三個轉(zhuǎn)速檔位,且以不同的檔位加工時,加工時長和相應(yīng)的機器能耗也不同。第一階段,讓所有機器以最高檔3檔進(jìn)行加工,此時加工速度最快,采用改進(jìn)的麻雀搜索算法優(yōu)化最大完工時間。在第一階段對最大完工時間實現(xiàn)優(yōu)化之后,在第二階段提出一種間隙檔位調(diào)整策略,在保證第一階段最大完工時間不變的前提下,通過降低部分工序的機器檔位,降低能源消耗,實現(xiàn)對總能耗的優(yōu)化。 間隙檔位調(diào)整策略的具體步驟如下: 1)初始化機器檔位編碼元素全部為最高檔位3,讓所有工序以最高檔3檔進(jìn)行加工,找出最快完工時間Cmax; 2)依此讀取工序編碼序列的每一位基因,轉(zhuǎn)換成相應(yīng)的工序Oij; 3)根據(jù)工序編碼依次獲得每道工序的加工設(shè)備以及標(biāo)準(zhǔn)加工時間(標(biāo)準(zhǔn)加工時間即機器以3檔加工的時間); 4)當(dāng)機器不是第一次被使用的時候,此時機器前后兩道相鄰工序之間有存在加工間隙的可能,若存在加工間隙,則轉(zhuǎn)5),否則轉(zhuǎn)11); 5)判斷機器前一道工序以最低檔1檔加工的加工時長是否小于等于機器前一道工序的標(biāo)準(zhǔn)加工時間與加工間隙之和,若是則轉(zhuǎn)6),否則轉(zhuǎn)8); 6)判斷機器前一道工序以最低檔1檔加工時,是否會影響最快完工時間Cmax,若是則轉(zhuǎn)8),否則轉(zhuǎn)7); 7)把機器前一道工序?qū)?yīng)的檔位編碼元素設(shè)置為1,機器前一道工序以最低檔1檔進(jìn)行加工; 8)判斷機器前一道工序以中間檔2檔加工的加工時長是否小于等于機器前一道工序的標(biāo)準(zhǔn)加工時間與加工間隙之和,若是則轉(zhuǎn)9),否則轉(zhuǎn)11); 9)判斷機器前一道工序以中間檔2檔加工時,是否會影響最快完工時間Cmax,若是則轉(zhuǎn)11),否則轉(zhuǎn)10); 10)把機器前一道工序?qū)?yīng)的檔位編碼元素設(shè)置為2,對機器前一道工序以中間檔2檔進(jìn)行加工; 11)機器前一道工序?qū)?yīng)的檔位編碼元素保持為3不變; 12)工序編碼序列基因是否讀取完畢,若是則轉(zhuǎn)13),否則轉(zhuǎn)2); 13)結(jié)束。 實驗在Intel Core i5-5200U、2.20 GHz CPU、8.00 G RAM、Windows 10 64位操作系統(tǒng)的筆記本電腦上運行。程序編譯和運行環(huán)境為:MATLAB R2020a。 參數(shù)設(shè)置:種群大小為100;算法最大迭代次數(shù)為500;AGV空載功率和負(fù)載功率分別為0.12 kW和0.15 kW;機器有3個檔位,給定檔位系數(shù)[1.5,1.2,1]分別對應(yīng)于1、2、3檔,三個檔位的加工時間分別為標(biāo)準(zhǔn)算例的時間乘以檔位系數(shù);機器的加工信息表參照文獻(xiàn)[8]的部分?jǐn)?shù)據(jù),其中每臺機器的功耗信息如表1所示。 表1 每臺機器的功耗信息 表1中每臺機器均有3個不同的檔位,具有不同的加工功率和空載功率,機器檔位越高所需功率越大。 為了驗證改進(jìn)麻雀搜索算法的有效性,筆者將改進(jìn)麻雀搜索算法(ISSA)與標(biāo)準(zhǔn)麻雀搜索算法(SSA)以及文獻(xiàn)[18]中的混合哈里斯鷹算法(hybrid harris hawk optimizer, HHHO)、改進(jìn)哈里斯鷹算法(improved harris hawk optimizer, IHHO)、哈里斯鷹算法(harris hawk optimizer, HHO)、灰狼優(yōu)化算法(grey wolf optimizer, GWO)和鯨魚優(yōu)化算法(whale optimization algorithm, WOA)進(jìn)行對比,對完工時間進(jìn)行優(yōu)化;每個算例運行20次,取20次的最優(yōu)值和平均值進(jìn)行比較。 各算法的對比實驗結(jié)果如表2所示。 表2 WOA、GWO、HHO、iHHO、HHHO、SSA和ISSA算法運行結(jié)果 從表2可以看出:在求解LA16算例時,除ISSA算法稍遜于HHHO這一個算法外,ISSA算法不論是求解最優(yōu)值還是平均值,效果均優(yōu)于其他5種算法;在求解另外9個算例時,DISSA算法不論是求解最優(yōu)值還是平均值,效果均優(yōu)于其他6種算法。此外,ISSA算法求解出的最優(yōu)解的個數(shù)也多于其他算法。 綜上可以看出,ISSA算法具有更好的尋優(yōu)能力和求解的穩(wěn)定性。 此處算法的改進(jìn)策略包括:1)采用反向?qū)W習(xí)策略初始化麻雀種群;2)在發(fā)現(xiàn)者位置更新后引入局部搜索策略;3)在麻雀搜索算法后引入模擬退火算法。 為驗證算法改進(jìn)策略的有效性,筆者采用上述三種改進(jìn)策略依次對文獻(xiàn)[18]中的10個作業(yè)車間標(biāo)準(zhǔn)算例進(jìn)行仿真實驗,對完工時間進(jìn)行優(yōu)化;每個算例運行20次,取20次的最優(yōu)值和平均值進(jìn)行比較。 麻雀搜索算法改進(jìn)策略對比結(jié)果如表3所示。 表3 麻雀搜索算法改進(jìn)策略對比 由表3實驗結(jié)果可以看出,標(biāo)準(zhǔn)麻雀搜索算法經(jīng)過反向?qū)W習(xí)策略初始化、局部搜索策略、模擬退火等一系列改進(jìn)之后,算法的尋優(yōu)能力和求解的穩(wěn)定性逐步增強,尤其是加入局部搜索策略之后,優(yōu)化效果最為顯著。由此可以證明,該算法改進(jìn)策略是有效的。 筆者分別選取FT10算例和LA36算例進(jìn)行說明。其逐步改進(jìn)策略的迭代曲線圖分別如圖4、圖5所示。 圖4 FT10迭代曲線圖 圖5 LA36迭代曲線圖 圖4和圖5顯示:經(jīng)過反向?qū)W習(xí)策略初始化改進(jìn)之后,算法的收斂速度加快,在相同的迭代次數(shù)下,能夠得到更優(yōu)的結(jié)果;經(jīng)過局部搜索策略之后,發(fā)現(xiàn)者通過擴大搜索范圍,搜索到了更優(yōu)的解;加入模擬退火算法之后,算法具有更強的跳出局部最優(yōu)的能力。 文獻(xiàn)[19]2876指出,運輸時間越大,對完工時間的優(yōu)化效果越明顯;并且為了嚴(yán)格驗證算法的有效性,選擇運輸時間最小的情況對算法有效性進(jìn)行驗證。 此處機器之間的距離越大,在AGV速度固定不變的情況下,運輸時間也就越長,工件被運輸?shù)较乱慌_機器M的時間將會越靠后,此時機器M上本道工序和前一道工序之間存在的加工間隙也就越大,機器M上前一道工序選擇降檔加工的可能性也就越大;反之,機器之間距離越小,運輸時間越短,工件被運輸?shù)较乱慌_機器M的時間將會越提前,此時機器M上本道工序和前一道工序之間存在的加工間隙也就越小,機器M上前一道工序選擇降檔加工的可能性也就越小。 為了嚴(yán)格驗證上述間隙檔位調(diào)整策略的有效性,筆者參照文獻(xiàn)[19]2876,選擇運輸時間最小的情況,對間隙檔位調(diào)整策略的有效性進(jìn)行驗證,即把裝載區(qū)和卸載區(qū)抽象為機器,設(shè)置相鄰兩臺機器之間的距離為單位1,且單位距離運輸時間為1。 有研究表明[19]2877,當(dāng)AGV數(shù)量達(dá)到工件數(shù)量的80%左右時,對完工時間的優(yōu)化效果是最好的,此時AGV數(shù)量足夠使用且不造成AGV的浪費。 因此,筆者設(shè)置AGV數(shù)量為工件數(shù)量的80%,并四舍五入取整。 第一階段,機器以最高轉(zhuǎn)速3檔進(jìn)行加工,采用改進(jìn)麻雀搜索算法對最大完工時間進(jìn)行優(yōu)化;第二階段,在保證第一階段優(yōu)化得到的最大完工時間最小值不變的前提下,使用間隙檔位調(diào)整策略,對總能耗進(jìn)行優(yōu)化[20-23]。 第一階段和第二階段優(yōu)化結(jié)果對比如表4所示。 表4 兩階段優(yōu)化結(jié)果 由表4可以看出:在第一階段,機器全部以3檔進(jìn)行加工,加工速度最快,此時優(yōu)化最大完工時間,得出最大完工時間的最小值和相應(yīng)的車間總能耗;在第二階段,在保證第一階段最大完工時間不變的同時,使用間隙檔位調(diào)整策略對部分工序的加工機器進(jìn)行降檔調(diào)整,實現(xiàn)了對車間總能耗的優(yōu)化。 以FT06算例為例,在第一階段對最大完工時間進(jìn)行優(yōu)化時,最大完工時間為68,總能耗545.29,其調(diào)度甘特圖如圖6所示。 圖6 第一階段優(yōu)化的FT06甘特圖 在第二階段使用間隙檔位調(diào)整策略之后,最大完工時間保持為68不變,總能耗降為527.67,其調(diào)度甘特圖如圖7所示。 圖7 FT06使用間隙檔位調(diào)整策略的甘特圖 從圖6和圖7的對比可以看出:在完工時間不變的情況下,能耗仍然減少了17.62,降低了3.23%,實現(xiàn)了綠色調(diào)度的目的。 由此可以證明,間隙檔位調(diào)整策略是有效的。 在考慮AGV運輸和機器轉(zhuǎn)速的基礎(chǔ)上,筆者建立了作業(yè)車間綠色調(diào)度模型,并設(shè)計了反向?qū)W習(xí)策略、局部搜索策略、模擬退火算法等多種改進(jìn)策略,采用改進(jìn)麻雀搜索算法對調(diào)度模型進(jìn)行了求解,采用兩階段優(yōu)化的方式對完工時間和能耗優(yōu)化進(jìn)行了研究,通過部分FT和LA基準(zhǔn)算例的仿真結(jié)果與其他算法進(jìn)行了實驗對比,驗證了改進(jìn)麻雀搜索算法的有效性。 研究結(jié)果表明: 1)采用反向?qū)W習(xí)策略生成麻雀初始種群,提高了種群質(zhì)量,加快了算法收斂速度;采用局部搜索策略和模擬退火可以提高麻雀算法的搜索深度,并獲取較強的跳出局部最優(yōu)的能力; 2)采用兩階段優(yōu)化的方式可以在完工時間優(yōu)化后不改變的基礎(chǔ)上,通過間隙檔位調(diào)整策略降低機器加工速度,可以有效降低能耗。在10個算例測試中,能耗最高降低5.18%,能耗最低降低1.13%,能耗平均降低2.70%; 3)通過FT和LA基準(zhǔn)用例,對麻雀算法改進(jìn)前后及其他算法進(jìn)行了實驗對比,證明了改進(jìn)麻雀算法的有效性,其尋優(yōu)能力和求解速度有明顯提升。在10個算例測試對比中,只有在LA16算例上,ISSA性能略差于HHHO算法,在其他算例上,ISSA性能均優(yōu)于其他6種算法。 在目前的研究中,筆者沒有考慮AGV的路徑規(guī)劃問題、AGV的電量及其充電問題,也沒有考慮機器的故障、AGV故障等特殊情況,這些將是筆者下一步研究工作的主要內(nèi)容。3 間隙檔位調(diào)整策略
4 仿真實驗與分析
4.1 實驗環(huán)境及參數(shù)設(shè)置

4.2 算法有效性驗證

4.3 算法改進(jìn)策略有效性驗證



4.4 間隙檔位調(diào)整策略有效性驗證
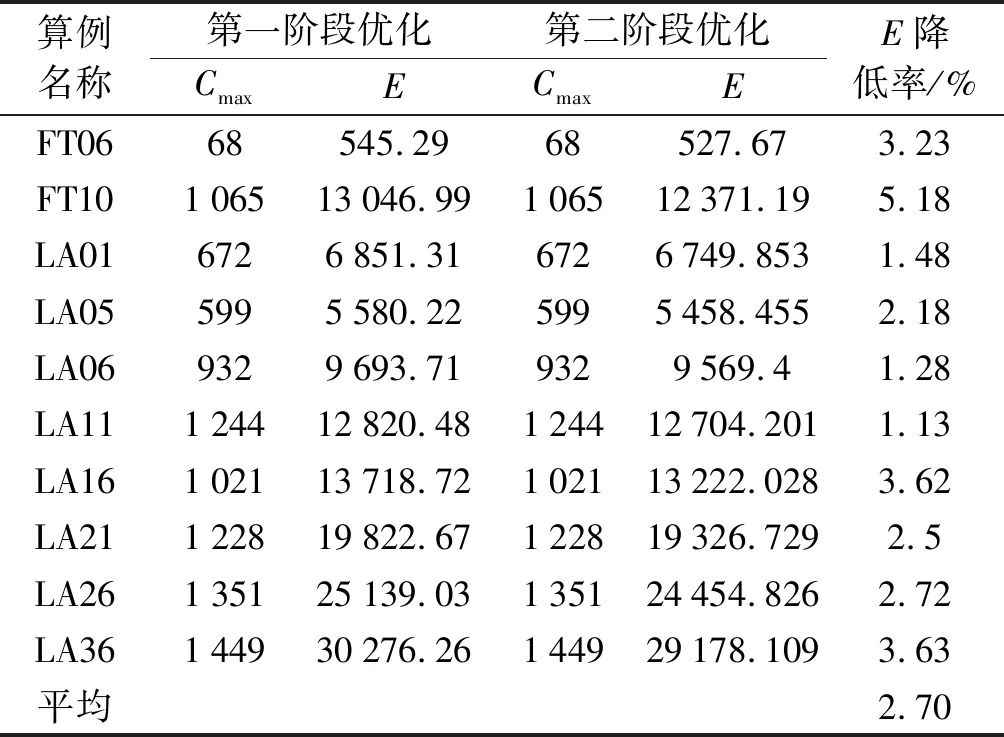


5 結(jié)束語

