擬MQ函數在物探數據處理中的應用

張一凡,劉海飛,柳建新,郭 鵬,劉 昕

(1.中南大學 地球科學與信息物理學院,長沙 410083;2.有色資源與地質災害探查湖南省重點實驗室,長沙 410083)

0 引言

地球物理觀測的數據都可視為空間、時間域離散的數字信號。在點距稀疏不均勻(如航空物探)、因客觀條件造成數據缺失(如地形因素)、儀器設備不穩定造成部分壞記錄的情況下,往往需要通過有效插值方法盡量規律性補足觀測數據集。另外,為避免數據解釋得到錯誤的認識,強噪音引起的異常數據需在數據處理中剔除,并盡量采用一種保光滑、保形狀的插值方法對真實數據進行恢復。線性插值、樣條插值等常規插值方法在地球物理數據處理中應用廣泛,但對于一些特殊場景,其插值光滑效果還需改進。

MQ函數(Multi-quadric function)最早由Hardy[1]于1971年提出,Franke[2]發現在29類散亂數據插值中,MQ函數的精確性、有效性、穩定性優于其它方法,然而利用MQ函數需要求解線性方程組且系數矩陣通常是病態的。因此,對MQ函數進行某種近似且避免求解線性方程組的方法逐漸引起重視,這種逼近函數被稱為擬MQ函數。Beatson 和 Powell[3]利用 MQ 函數提出了三種單變量的擬MQ插值算子QA、QB、QC,并得到了它們的誤差,同時證明擬插值算子QC具有很好的線性再生性和插值精度。Wu和Schaback[4]對QC進行改進,提出了一種新的擬MQ插值算子QD,并討論了它們的逼近階和保形性。后來,該插值算子被廣泛應用于求解偏微分方程[5-9]。此外,Ling[10]在Wu和Schaback工作的基礎上,提出了一種多水平單變量擬MQ插值算子。Ling[11]還利用空間維數分離方法,構造了擬MQ插值算子QR。Jiang等人[12]在擬插值算子QD的基礎上構造了一種高精度的擬插值算子QW,該算子具有保線性且具有很高的精度。高文武[13]討論了基于導數信息的擬MQ插值的構造方法,并用該方法構造了一個擬MQ插值算子,證明了該算子的收斂性及保形性。

擬MQ函數無需求解線性方程組,根據離散節點能快速直接給出插值結果,還具有良好的保形性、計算穩定、計算量小等優點。因此,在過去的幾十年里,擬MQ函數取得了一定的發展[14-16]。但整體而言,該函數在地球物理領域的應用研究較少。

筆者利用Wu和Schaback[4]提出的擬MQ插值算子QD,分析整理了其在物探數據處理中的應用,主要包括擬合地表高程、高密度電法數據插值與平滑、電測深曲線插值與求導等,取得了良好的處理效果,證實了該函數在物探數據處理中的有效性和實用性。

1 基本理論

1.1 MQ函數

f(xj),j=0,1,…,n

(1)

式中:φ(x-xi)為MQ函數,對于一維插值問題,其形式為:

(2)

式中:s為形狀參數,決定了曲線的銳度。若相鄰插值結點的最大間隔為h,s相對h保持相關且趨于零可獲得更高的準確性[1]。將式(1)寫成矩陣形式:

Ac=z

(3)

其中:

A=

求解線性方程(3),即可求得解向量cn×1。將解向量cn×1及待插點xj代入式(1),便可計算出待插點xj的值f(xj)。

1.2 擬MQ函數

為避免求解線性方程組,Beatson 和 Powell[3]利用 MQ 函數提出了三種單變量擬插值算子QA、QB、QC。Wu和 Schaback[4]在此基礎上給出了逼近階和保形性較好的擬插值算子QD。

(4)

擬插值算子QB滿足:

f(xn)βn(x)

(5)

f(xn)αn(x)

(6)

為了進一步提高插值精度,相較于擬插值算子QA和QB,還可以引入更多條件定義擬插值算子QC:

QCf(x)=QBf(x)+f′(x0)γ0(x)+

f′(xn)γn(x)

(7)

將其改寫為:

QCf(x)=f(x0)β0(x)+f′(x0)γ0(x)+

f(xn)βn(x)

(8)

Beatson 和 Powell[3]對三種擬插值算子進行了大量測試,表明QC的插值精度最高。但應用QC需要事先知道邊界點的導數,實際應用中很難滿足此條件。為克服這一缺點,Wu和Schaback[4]對其進行改進,定義了一種具有保單調性和保凸性且不需要知道邊界點的導數值的擬插值算子QD,它的逼近效果與QC相當。擬插值算子QD的定義如下:

QDf(x)=f(x0)a0(x)+f(x1)a1(x)+

f(xn-1)an-1(x)+f(xn)an(x)

(9)

可將式(9)展開為:

(10)

由于大量實際工程數據均無法給出插值端點處的導數值,相比之下QD具有更好的應用價值。

1.3 擬MQ函數的導數形式

常規插值方法往往只保證函數值插值精度,但很多地球物理方法需要對數據的數值微分進行分析以突出弱異常,這對插值方法提出了更高的要求。對于式(10),其一階導數為:

QDf′(x)=

(11)

二階導數為:

(12)

通過式(11)、式(12),便能推算出離散點的導數值,從而在觀測曲線中發揮提取弱異常的優勢。

2 擬MQ函數在物探數據處理中的應用

2.1 在地表高程插值中的應用

以山東某金礦地球物理勘查剖面的地表高程數據為例,該剖面已知的地表高程點有64個,橫向分布范圍為[0～4 460],并且呈不等間距分布。以10 m為間隔從0到4 460均勻采樣作為待插結點,采用三次樣條函數及擬MQ函數對地表高程點分別進行插值。插值結果如圖1、圖2所示。

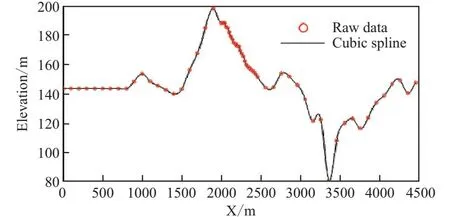
圖1 三次樣條函數的插值結果Fig.1 Interpolation results of cubic spline functions

圖2 擬MQ函數的插值結果Fig.2 Interpolation results of quasi-MQ functions

可以看出:在利用三次樣條函數進行插值時,當函數值變化較大且插值結點較稀疏時,會在插值結點附近引起插值曲線的震蕩(如3 160 m～3 260 m),而擬MQ函數則避免了這一缺陷。當形狀參數s=0時,插值曲線與原始高程曲線完全重合。當s相對h(相鄰插值結點的最大間隔)逐漸增大時,插值曲線在階躍點處的光滑程度也隨之增大,但總體形態與原曲線保持一致。因此,說明擬MQ函數具有良好的保形性和保單調性。對于形狀參數s的選擇問題,目前沒有一個量化的選擇依據,但為了獲得更高的準確性,s與h保持相關且趨于零時是最有利的[1]。若將擬MQ函數用于高程擬合,形狀函數不宜取得過大(s

2.2 在高密度電法數據處理中的應用

在高密度電法勘探中,常常因電極接地電阻過大或淺地表不均勻體的影響,使得觀測數據含有一定程度的干擾噪聲(淺部因素也會影響深部數據)。在布設的電極陣列中,同一根電極可能會作為供電電極或測量電極,如果某個電極接地電阻大,對于供電回路,將導致供電電流不穩定對于測量回路,將產生讀數不穩定,直接影響著數據的觀測精度,最終造成繪制的視電阻率擬斷面圖存在虛假或冗余異常。為壓制高密度電法數據的干擾噪聲,筆者嘗試采用擬MQ函數對高密度數據進行降噪處理。

以邵懷高速公路某段高密度電法勘查為例,以檢驗擬MQ函數的降噪效果。該勘查段測線長度595 m,120道電極,點距5 m,測量層數39層,圖3(a)為原始高密度數據繪制的擬斷面圖,可以看出在斷面圖中存在較多冗余異常。采用擬MQ函數對該數據斷面進行逐層降噪處理,考慮高密度電法的觀測特點,以觀測點距(5 m)作為形狀參數,圖3(b)為處理后的高密度數據繪制的擬斷面圖,從斷面圖中可以看出,視電阻率等值線的平滑特征得到明顯改善,更有助于數據分析和解釋。

圖3 高密度視電阻率斷面處理前后對比圖Fig.3 Comparison before and after HD apparent resistivity section procession

2.3 在電測深曲線數據處理中的應用

由于利用數值微分可以提取地球物理原始數據曲線中的弱異常信息的特點,對新疆清河縣地下水的分布情況研究分析。以其中一條電測深曲線為例,利用擬MQ函數對其進行計算一維加密插值(Fitting curve),進而獲得更可靠的一階導數(FD)和二階導數(SD),具體如圖4 所示。

圖4 基于擬MQ函數的電測深數值微分曲線Fig.4 Numerical differential curve of electrical sounding based on quasi-MQ function

可以看出:在極距AB/2為90 m和125 m的位置存在微弱的低阻異常,通過對電測深曲線計算一維插值、一階導數和二階導數,使這兩個位置的弱異常幅度得到增大。結合該區地質資料及鉆探施工條件,在此處開展了鉆孔工作。發現在深度20 m以內為第四系,20 m～75 m以內為凝灰質砂巖,75 m～130 m以內為花崗巖,在深度130 m處打到構造破碎帶,含水量較大,由于水壓過大導致沖擊鉆探方法難于施工,并于135 m深度處終孔,未打穿斷層破碎帶,終孔孔徑110 mm。采用32 m3/h水泵進行抽水試驗,靜水位2.1 m,動水位28 m,水位降深25.9 m,經計算該鉆孔出水量為46.3 m3/h(1 111.2 m3/d)。因此,利用擬MQ函數可以較好提取物探原始數據曲線中的弱異常信息。

3 結論

通過擬MQ函數在物探數據處理中的應用研究,得到以下結論:

1)利用擬MQ函數擬合地表高程,整體曲線較光滑,能很好地逼近地表形態,并隨著形狀參數的增大光滑程度加大,仍能保留原始數據的整體特征,驗證了擬MQ函數具有良好的保形性及保單調性。

2)利用擬MQ函數對高密度數據進行插值平滑處理,能達到很好的降噪效果,從而有利于后續數據的分析與解釋。

3)利用擬MQ函數對電測深曲線進行插值、一階求導、二階求導處理,能明顯放大地下弱異常的幅度,有利于提取物探原始數據曲線中的弱異常信息。

隨著理論研究和工程實踐的共同進步,擬MQ函數有望在地球物理數據處理中發揮更大作用,顯示出更多優勢,成為一種常規數學工具。