聲空化條件下傳動液體積彈性模量的時空演變

陳益宏，許滄粟，李孝祿，李運堂，陳源，金杰，龐文

(1.中國計量大學機電工程學院，浙江杭州 310018；2.浙江省智能制造質量大數據溯源與應用重點實驗室，浙江杭州 310018；3.浙江大學能源工程系，浙江杭州 310027；4.中廣核太陽能德令哈有限公司，青海德令哈 817000)

0 前言

體積彈性模量是指液體所受壓力與體積變化量的比值，表征了傳動系統中傳動液的抗壓縮能力[1]。體積彈性模量的值越大，傳動液的抗壓縮性能力越強。當系統處于高速運作的啟停環節時，體積彈性模量會直接影響傳動系統的動態特性，甚至會造成機器零部件的損壞[2]。因此，需引入有效體積彈性模量來準確反映系統實際工況。而有效體積彈性模量主要受傳動液工作壓力、含氣率和溫度的影響[3-4]。由于空化效應、低壓和高溫會導致傳動管中的氣體含量升高，有效體積彈性模量變小，從而對壓力精準傳遞產生影響[5]。

傳動液壓力和含氣率的時空演變過程較為復雜。CATANIA等[6]使用均相流模型，避免了計算氣相和液相之間的滑移速度，比較了預測數據與實驗數據(利用Moehwald-Bosch MEP2000-CA4000高性能試驗臺)，結果表明：即使在空化引起的不連續情況下，也可以高精度地模擬壓力波傳播。CATANIA等[7]還利用流體控制方程，考慮壓縮效應引起的溫度變化，提出了一種新的正壓空化模型來預測壓力波動、含氣率和溫度的變化，并與實驗結果進行了比較，結果證實了所研究的模型在模擬聲空化開始和結束時的有效性和魯棒性。在此基礎上，FERRARI[8]提出一種將Zielke層流頻率相關摩擦模型擴展到湍流的原始方法，并將其應用于動量平衡方程，結果表明：所提出的模型能正確地預測壓力波振幅相對于時間的衰減。

傳動液壓力和含氣率的預測對研究體積彈性模量的時空演變起到關鍵作用。魏超等人[9]為提升油液壓縮與膨脹過程動態特性分析的準確性，將含氣量變化納入有效體積彈性模量的動態模型中，并對比了4種穩態模型(Wylie、Nykanen、Ruan和AMESim模型)在高、低壓時的適用性和變化特性，結果表明：在Henry定律下，動態模型預測的精度更高。唐東林等[10]推導了含氣油液有效體積彈性模量理論模型，并將理論模型的數值模擬結果與實驗數據對比，結果表明：在油液壓力小于空氣分離壓時，有效彈性模量隨初始含氣量升高而降低；在大于空氣分離壓的范圍內，有效彈性模量隨升壓時間的增加而降低。李孝祿等[11-12]基于有效體積彈性模量理論模型，利用高速攝像機獲得不同類別流體(泡狀流、彈狀流、塞狀流和環狀流)的狀態圖，通過圖像處理分析了含氣率和有效彈性模量之間的關系，結果表明：制動液的有效彈性模量隨含氣率的升高而降低，且在含氣率大于1%時，為滿足制動效果需提高其制動壓力。袁曉明等[13]基于完全空化模型，以改進的Henry定律提出了更高精度的動態體積彈性模量預測模型(Model 1)，與3種穩態模型和Sakama動態模型進行對比，并和實驗數據進行比較，結果表明：Model 1動態模型與實驗結果更接近，提高了預測的準確性。

上述學者僅在時間域上對體積彈性模量進行了預測，并未在空間上進行預測。因此，本文作者考慮空氣空化、蒸汽空化和偽空化3種空化效應和由壓縮效應引起的溫度變化，分別建立了傳動管中體積彈性模量均相流模型和動態模型，利用氣液混合物的流體狀態方程來連接壓力項，并結合Roe格式分解和Steger Warming通量分裂方法，提出一種新的數值求解方法來預測不同空化區中的壓力波傳播和瞬態氣體含量的變化，并預測體積彈性模量的時空演變。討論壓力、含氣率和溫度對動態體積彈性模量的影響，并比較兩種模型的區別。

1 數學模型

1.1 均相流模型

在傳動管中，考慮傳動管內壓縮前后傳動液的質量守恒以及流動對管壁剪切應力的影響，以密度ρ和動量ρu作為守恒變量，采用質量守恒方程和動量守恒方程對可壓縮氣液兩相流動進行數學建模，得到守恒型流體動力學方程組，并用矩陣的形式表達：

(1)

式中：ρ為混合物流體密度，kg/m3；u為傳動液流速，m/s；p為傳動液壓力，Pa；t為時間變量，s；f為傳動液流動阻力系數，當雷諾數Re≤2 000時，流動為層流，f=64/Re；當雷諾數Re>2 000時，流動為紊流，f=0.316/Re0.25。

為研究動態體積彈性模量與傳動液在壓縮膨脹過程中氣體含量的關系，引入含氣率的表達式：

(2)

式中：χ是指空氣g或蒸汽v；α為含氣率，%；ρl為傳動液密度，kg/m3。

傳動液的密度按照流型的不同可分別表示為均勻泡狀流和分層流的函數：

(3)

理想氣體的狀態方程由氣體實驗定律和阿伏伽德羅定律給出：

P=ρχrχT

(4)

式中：r為氣體常數，J/(mol·K)；T為溫度，K。

對于正壓流流動，通常在空化區，溫度T是壓力p的函數，T=T(p)。在式(3)中傳動液的密度是壓力p和溫度T的函數，ρl=ρl(T,p)。

對于可壓縮流體的一維流動，在忽略邊界交換熱量的前提下，溫度場用能量守恒方程來表示：

(5)

式中：h為系統單位質量的焓，J/kg；Q為系統內單位質量的黏性功率耗散，J/(kg·s)。

在等熵條件下，考慮純液體流動時液壓管內的壓縮帶來溫度的變化，將任何過程中液體的壓力與溫度聯系起來，得到以下關系式[14]：

(6)

式中：Cp為定壓比熱容，J/(kg·K)；γT為等溫聲速，m/s；φ為熱膨脹系數，1/K；ET為等溫體積彈性模量，Pa。

傳動液聲速γ與體積彈性模量E有著密切關系，因此給出純液體流動、空氣空化和蒸汽空化時的聲速表達式：

(7)

在氣液兩相條件下，給出體積彈性模量E與聲速γ和含氣率α之間的關系：

(8)

均相流模型需要增加氣液混合物的狀態方程，才能使得方程組封閉。此研究中，將流體看作是純液體和一定量的空氣和蒸汽的均質混合物，為求解氣液兩相流中的壓力項，需要用氣液混合物流體狀態方程連接。給定一個氣液質量流量比μ，那么混合物流體密度ρ、氣體密度ρχ和含氣率α均為壓力p和溫度T的函數。式(6)給出了壓力與溫度的關系，從而可以得出混合物流體密度和壓力p、溫度T之間的關系：

(9)

式中：μ為氣液質量流量比，%。

通過混合物流體狀態方程將壓力p與混合物流體密度ρ聯系起來，由于管內流動會產生壓降，為此需給出壓力梯度的表達式：

(10)

1.2 體積彈性模量動態模型

在實際工作過程中，有效體積彈性模量表征傳動液的抗壓縮性，其定義為

E=-V(dp)/(dV)

(11)

抗壓縮特性主要受流體的壓力、含氣率和溫度影響，且隨著流體被壓縮，其溫度會增高，流體趨于膨脹，進而產生附加壓力。因此，出于對上述3種因素的考慮，將純傳動液(不含空氣與蒸汽)的有效體積彈性模量[15]簡化為

Ec=E0+κΔp+ηΔT

(12)

式中：Ec為純傳動液的有效體積彈性模量，Pa；E0為標準狀態下的有效體積彈性模量，Pa；κ為壓力變化系數；η為溫度變化系數。

在傳動液傳動過程中，由于傳動液本身溶解了部分空氣和傳動管中存在著部分空氣，在空化過程中產生的空氣與蒸汽會使含氣率升高，導致由壓力變化引起的傳動液體積改變，影響有效體積彈性模量。

考慮到純傳動液、空氣和蒸汽3種成分在過程中的變化，且壓力、含氣率和溫度隨時間變化，引入動態體積彈性模量的表達式，將式(11)改寫為

(13)

在標準大氣壓p0下的氣體壓縮方程為

(14)

式中：Vg0和Vv0分別為標準大氣壓p0下的空氣體積和蒸汽體積，m3。

純傳動液的體積由以下表達式[16]給出：

Vl(t)=Vl0e(p-p0)/Ec

(15)

將式(14)、(15)關于壓力p求導，代入式(13)得：

(16)

2 求解方法

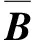
(17)

采用Roe格式分解，對特征向量進行處理，得到流速u和密度ρ的平均表達式：

(18)

采用Steger-Warming通量分裂法在空間上進行流通量的離散，對時間項采用歐拉向前差分。差分格式如下：

(19)

3 數值結果與分析

3.1 傳動液的物性參數

CATANIA等[7]以高壓燃油噴射系統為研究對象，包括燃油泵、壓力管和單彈簧噴油器，并利用ISO 4113試驗油模擬柴油。在燃油泵出口和噴油器進口附近設置了一個壓阻傳感器，通過實驗收集兩端的壓力數據。在此研究中，ISO 4113試驗油[7]用于模擬純傳動液的密度、聲速和熱膨脹系數，這些參數是溫度T和壓力p的函數。

式(1)的初值條件為

(20)

此研究使用了圖1所示的壓力邊界條件[7]。

圖1 壓力邊界條件[7]

模擬中使用的其他參數如表1所示。初始氣體含量設置為1.425%，包括溶解在傳動液中的氣體和氣泡形式存在的氣體。模擬中使用的網格大小為0.01 m×2.5 μs(480萬個網格)。通過入口和出口壓力波的壓力差來模擬傳動液的壓縮和膨脹過程。

表1 模擬計算所需的參數

3.2 體積彈性模量的時空演變

為了清晰地表達傳動液體積彈性模量的時空演變，在圖2中繪制了沿時間和管道軸向方向的體積彈性模量變化的三維表示和映射投影。可以看出：體積彈性模量最大達到1 570 MPa。體積彈性模量主要受壓力、含氣率和溫度的影響，在時空中發生變化，且在空化區域的變化尤為劇烈。在x=0～0.51 m、t=0.1～0.14 s以及t=0～0.06 s、t=0.16～0.24 s的部分區域，體積彈性模量為較低值。

圖2 體積彈性模量變化的三維表示和映射投影

3.3 壓力對動態體積彈性模量的影響

圖3為傳動液壓力變化的三維表示和映射投影。可以看出：壓力波在傳動管中傳播，在傳動液初始壓力為0.6 MPa的條件下，最大壓力可達到約50 MPa。當t=0.1～0.14 s、x=0～0.51 m時，傳動液壓力顯著下降，其壓力接近甚至低于飽和蒸汽壓，蒸汽的局部空化效應發生在傳動管入口附近。隨后，沿著管道軸向方向，傳動液壓力開始增加。從壓力波動的角度來看，傳動液壓力的變化趨勢與CATANIA等[7]的結果相同。

圖3 壓力變化的三維表示和映射投影

圖4為均相流模型與動態模型下的動態體積彈性模量在管內不同位置隨壓力的變化。可以看出：當壓力小于1 MPa，管內任意位置的動態體積彈性模量隨著壓力的變化相同；當壓力在1～10 MPa內時，動態體積彈性模量隨壓力增大而快速增大，其變化率在不斷減小；當壓力大于10 MPa時，在均相流模型中，動態體積彈性模量隨壓力緩慢增加，而動態模型下的動態體積彈性模量最終穩定在1 290 MPa。

圖4 管內不同位置的體積彈性模量隨壓力的變化

圖5為均相流模型與動態模型下的動態體積彈性模量比較結果。可以看出：在空氣空化后的高壓區，均相流模型得到的動態體積彈性模量要高于動態模型。這是由于均相流模型直接以能量守恒方程得到溫度變化，在這個階段，壓力從低壓區快速傳播至高壓區，溫度迅速升高；而動態模型以升溫系數與溫差的比例關系得到溫度變化，在這個階段溫度趨于平穩。這使得純液體的有效體積彈性模量在低壓區向高壓區轉變的過程中會有較大差異，最終影響混合物的動態體積彈性模量。在低壓區，兩種模型的預測結果吻合，而在蒸汽空化后的高壓區，兩種模型的預測結果存在較小的差別。

3.4 含氣率對動態體積彈性模量的影響

圖6為含氣率變化的三維表示和映射投影，其被分為3個區域。深黃色區域代表空氣空化區，主要發生在整個管道的0～0.04 s和0.2～0.24 s時間間隔內。壓力下降至空氣分離壓以下，氣泡迅速產生，最大含氣率約為1.425%。橙紅色區域表示蒸汽空化區。這一過程主要發生在x=0～0.51 m、t=0.1～0.14 s。隨著時間的推移，空化區移動到管的中部并不斷收縮，蒸汽空化程度在x= 0.45 m左右達到最大，含氣率最大達到1.925%，這與文獻[7]中的最大含氣率相近。紫色區域代表偽空化區，占據了大部分時空區域，含氣率隨壓力增大而減小。

圖6 含氣率變化的三維表示和映射投影

圖7為均相流模型與動態模型下的動態體積彈性模量在不同初始含氣率下隨壓力的變化。可以看出，給定初始含氣率的條件下，動態體積彈性模量隨著壓力的增大而增大。當壓力小于1 MPa時，動態體積彈性模量變化率隨初始含氣率增大而減小。當壓力在1～10 MPa內時，動態體積彈性模量隨壓力增大而快速增大，其變化率逐漸減小。當初始含氣率小于5%，動態模型下的動態體積彈性模量的變化曲線要比均相流模型所得曲線更加平滑。而當初始含氣率為10%，動態模型下的動態體積彈性模量變化率在5 MPa和7.5 MPa的壓力下突增。當壓力大于10 MPa，均相流模型中，動態體積彈性模量隨壓力緩慢增加。而在動態模型中，隨著初始含氣率的降低，動態體積彈性模量更快趨于平穩，這與文獻[9]中的趨勢一致。

圖7 不同初始含氣率下動態體積彈性模量隨壓力的變化

圖8為均相流模型與動態模型下管內不同位置的動態體積彈性模量隨含氣率的變化。可知：管道入口與出口附近的動態體積彈性模量隨含氣率的增加而逐漸減小。當α<0.2%時，管道中間部分的動態體積彈性模量迅速降低，這是因為這些位置的壓降過快。當α=0.2%～1%時，動態體積彈性模量隨含氣率的增加呈線性下降的趨勢。當α>1%時，管內任意位置的動態體積彈性模量變化一致。由此可以看出：在偽空化區，含氣率會影響動態體積彈性模量的變化率，而在空氣和蒸汽空化區幾乎沒有影響。但在空氣和蒸汽空化區的動態體積彈性模量更低，更不利于壓力的傳遞。

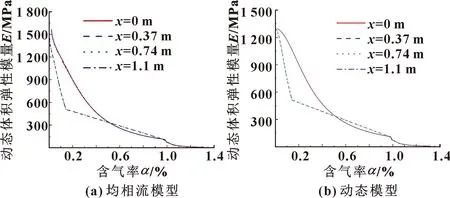
圖8 管內不同位置的動態體積彈性模量隨含氣率的變化

3.5 溫度對動態體積彈性模量的影響

圖9為傳動液溫度變化的三維表示和映射投影。溫度隨時間變化的最大幅值接近6 K，而CATANIA等[7]獲得了約7 K的溫度變化。在此研究中，未考慮空化區氣液相變和外部交換熱產生的熱量，但模擬溫度變化的最大幅值接近CATANIA等的結果。映射投影表明，正向流動中的溫度增速比反向流動更快。此外，蒸汽空化區中的溫度變化小于偽空化區中溫度變化。

圖9 溫度變化的三維表示和映射投影

圖10為均相流模型與動態模型下的動態體積彈性模量在不同初始溫度下隨壓力的變化。可知，當壓力小于1 MPa時，均相流模型中，不同初始溫度下的動態體積彈性模量變化相差不大。在動態模型中，初始溫度為293.15、353.15 K時，動態體積彈性模量呈線性增長，而初始溫度為308.15、323.15、338.15 K時，動態體積彈性模量僅在0～ 0.4 MPa內呈線性增長。當壓力在1～7.5 MPa內時，均相流模型中，動態體積彈性模量隨初始溫度增大而減小；而在動態模型中，當壓力在0.4～1.0 MPa內時，初始溫度在338.15～353.15 K內，動態體積彈性模量隨初始溫度增大而增大。當壓力大于7.5 MPa時，均相流模型中，動態體積彈性模量呈緩慢線性增長；而在動態模型中，動態體積彈性模量趨于穩定。

圖10 不同初始溫度下體積彈性模量隨壓力的變化

4 結論

傳動液中常含有空氣和蒸汽，在壓力波動的情況下傳動液含氣率隨之發生變化。含氣率的變化影響傳動液動態體積彈性模量，進而影響傳動系統的精準調控。為此，建立了均相流模型預測體積彈性模量的時空演化以及動態模型預測動態體積彈性模量，分析壓力、含氣率和溫度對動態體積彈性模量的影響，并將均相流模型和動態模型的預測結果進行對比。結果表明，均相流模型適用于低壓條件，而動態模型在高壓區也同樣適用。

(1) 當壓力小于1 MPa時，動態體積彈性模量隨壓力增大而增大。當壓力在1～10 MPa內時，動態體積彈性模量隨壓力增大而快速增大，其變化率不斷減小。當壓力大于10 MPa時，在均相流模型中，動態體積彈性模量隨壓力增大而呈線性緩慢增長趨勢；而在動態模型中，氣體將不斷溶解，動態體積彈性模量隨壓力增大而穩定在1 290 MPa。

(2) 動態體積彈性模量隨含氣率增大而減小，其變化率不斷減小。當初始含氣率小于5%時，動態模型預測動態體積彈性模量-壓力曲線相比均相流模型更平滑，而初始含氣率在10%的情況下，均相流模型的預測曲線更平滑。

(3) 動態體積彈性模量隨溫度增大而減小，其變化率不斷減小。在低壓區，當初始溫度為293.15 、353.15 K時，兩種模型預測結果相同。當壓力大于7.5 MPa，均相流模型中，動態體積彈性模量呈緩慢線性增長，而在動態模型中，動態體積彈性模量趨于穩定。