混合策略改進鯨魚優化算法在圓柱度誤差評定中的應用

呂星辰，鄭鵬，程亞紅，鄭嘉琦

(1.鄭州大學機械與動力工程學院，河南鄭州 450000；2.鄭州大學國際學院，河南鄭州 450000)

0 前言

隨著現代制造業的高速發展，精密軸類零件成為機械產品的重要組成部分。因為它往往需要配合起來使用，因此不僅要滿足尺寸精度要求，同時還要滿足形位精度要求。其中圓柱度誤差是衡量這類零件形狀誤差大小的主要指標，它也直接影響到零件的工作精度和系統的壽命。因此如何能夠快速、準確、高效地實現圓柱度測量和評定就顯得尤為重要。

在新一代產品幾何技術規范(GPS)中，根據理想要素擬合方法的不同，圓柱度誤差評定方法主要分為最小二乘法(Least Square Cylinder，LSC)、最大內接柱法(Maximum Inscribed Cylinder，MIC)、最大外接柱法(Minimum Circumscribed Cylinder，MCC)和最小區域法(Minimum Zone Cylinder，MZC)。在眾多評定方法中[1]，最小二乘法較為簡單快捷，但只是近似評定，在生產活動中容易造成誤判；而最小區域法是研究熱點，因其符合最小條件準則，所以通常在誤差評定發生爭議時起到仲裁作用[1]。

對于圓柱度誤差及其優化算法，國內外眾多學者已經進行了深入的研究。王瑞[2]建立了圓柱度誤差評定的線性規劃模型，該模型將非線性模型線性化，方便求解，但因略去高階項而存在模型誤差。溫文炯、溫英明[3]采用Newton法及Gauss消去法求解非線性方程組來評定圓柱度誤差，并通過實驗對比最小二乘法，證明該算法過程簡便實用，結果具有唯一性。郭慧等人[4]將改進的遺傳算法應用于圓柱度誤差的評定中，引入多種群的遷移策略有效提高全局搜索能力，通過實驗對比了各個模型的精度，驗證了其可行性。史栩屹等[5]設計了一種二次插值鯨魚優化算法，通過與其他優化算法對比，驗證了其具有較快的收斂速度和較好的精度。綜上，這些先進的優化算法均可以對圓柱體進行全局尺寸評定，但其收斂速度及穩定性依然有待提高。

根據座頭鯨圍捕獵物的行為，MIRJALILI、LEWIS[6]提出了鯨魚優化算法，其原理通俗易懂，參數設置較少，但算法容易陷入局部最優，收斂速度較慢。本文作者提出一種混合策略改進的鯨魚優化算法，進一步提高算法的收斂速度和精度。

1 圓柱度誤差評定模型

對于圓柱度誤差的評定，通常采用截面法，即確定提取窗口在圓柱軸向的起止范圍后，對窗口內多個平行橫截面上沿周向進行采樣[7]，然后通過求解不同截面上各測點的徑向偏差值來反映圓柱零件在該截面處相對于理想要素的變動量，進而得到圓柱度誤差。

1.1 數學模型的建立

如圖1所示，首先，建立Oxyz空間坐標系，設圓柱零件的回轉軸為z軸，評定基準軸線為理想圓柱軸線L。然后，沿z軸方向等距截取若干個平面，各個截面沿周向等距采樣，其坐標表示為Pij(Rij，θij，zi)，理想軸線L與xOy平面交點為O1(x，y，0)，它相對于z軸的傾斜角為γ，分別用γx和γy來表示傾斜角在xOz、yOz平面上的投影分量。

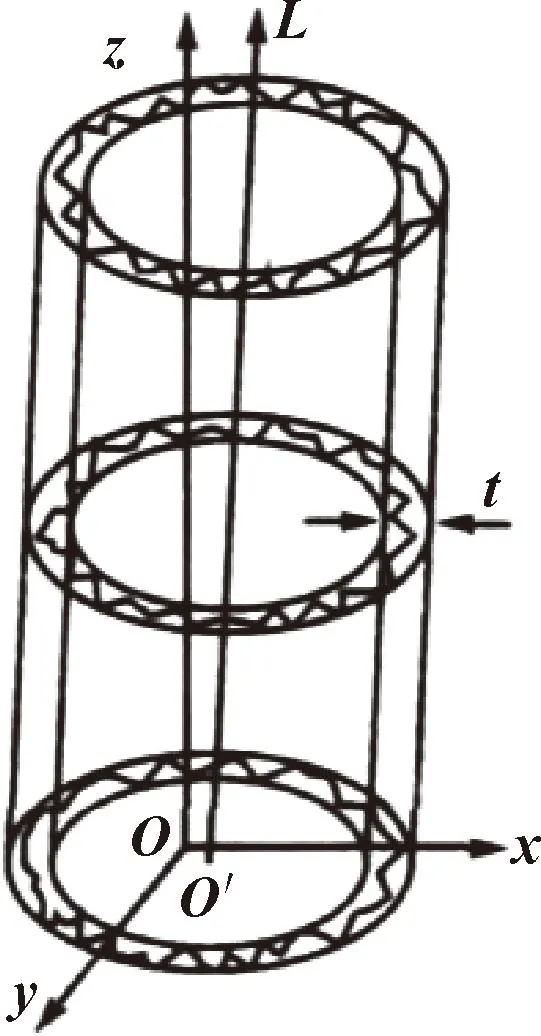
圖1 圓柱度幾何模型

則各測點相對于理想軸線的坐標可以表示為

(1)

那么各測點到軸線L的距離可以表示為

(2)

將上式進行泰勒展開，略去高階項，可簡化為

rij=Rij+(x+αzi)cosθij+(y+βzi)sinθij

(3)

其中：α=tanγx，β=tanγy。

1.2 圓柱度誤差的包容評定

包容評定分為雙包容和單包容(包括外包容和內包容)。以雙包容為例，即被測實際要素被兩同軸的理想圓柱面包容，當兩理想圓柱面徑向偏差達到最小時，差值f就是圓柱度誤差。因此通過前述公式可知，不斷尋找最優理想軸線L的位置，使各測點均落在由max(rij)和min(rij)構成的理想圓柱曲面內，且要保證其差值最小化，便可得到圓柱度誤差值[8]。

雙包容評定模型為

Fmin(x，y，α，β)=min(max(rij)-min(rij))

(4)

外包容評定模型為

Fmin(x，y，α，β)=min(max(rij))

(5)

內包容評定模型為

Fmin(x，y，α，β)=min(-min(rij))

(6)

2 混合策略改進鯨魚優化算法

在自然界中，座頭鯨通常以群居為主。在捕食過程中，首先鯨群會將獵物團團包圍，然后通過螺旋上升并吐出氣泡的方式來收縮包圍圈，直到捕食成功。根據這種行為，鯨魚優化算法將捕食過程分為包圍收縮、螺旋上升和隨機游動3個搜索機制。

對于傳統的鯨魚優化算法，為了解決其容易陷入局部最優解和收斂速度相對較慢的問題，以及增強其全局搜索能力，將算法在種群初始化階段引入Tent混沌映射來優化初始種群質量；在包圍收縮階段引入非線性參數來加速收斂；在螺旋上升階段引入自適應權重系數提高算法局部搜索能力；在隨機游動階段引入萊維飛行提高算法全局搜索能力。其詳細介紹在以下小節中進行展示[9-11]。

2.1 種群初始化

設算法的搜索空間為d維，種群中有n只鯨魚個體，最大迭代次數為T，變量的上下限分別為ub和lb，則第t次迭代中第i只個體表示為Xi(t)=(xi，1，xi，2，…，xi，d)，則鯨魚優化算法通過隨機數來生成初始種群，如下式：

X=(ub-lb)·rand(0，1)+lb

(7)

(8)

其中：ε=0.7。且要避免初值xn與參數ε相等，否則就不再是混沌系統，將會演化為周期系統。那么式(7)將改進為

X=(ub-lb)·f(xn)+lb

(9)

2.2 包圍收縮

包圍收縮搜索機制是鯨魚種群向著最優個體Xbest(t)游動來更新位置。公式如下：

(10)

其中：a為線性因子，隨著迭代次數從2線性減小到0，且系數向量A在該階段的模小于1。但為了加快收斂速度，避免陷入局部最優，在此將上述線性因子改為非線性的，使其前期變化迅速，而后期變化緩慢，從而達到目的。公式如下：

(11)

2.3 螺旋上升

螺旋上升搜索機制是鯨魚種群通過螺旋游動來更新其位置并通過吐出氣泡的方式來收緊獵物的移動空間。該階段位置更新方式如下：

(12)

其中：b為決定螺旋形狀的參數，通常取1；l為[-1，1]間的隨機數。

隨著迭代次數的增加，氣泡網會逐漸縮小，容易使算法陷入局部最優解中。為了使全部獵物均被收縮在包圍圈內，加入一個權重w，自適應地去更改鯨魚收緊獵物的移動范圍，達到當w較小時縮小包圍范圍、w較大時擴大包圍范圍的效果。

w=rand(0.5，1)+ft/fg

(13)

其中：fg為當前全局最優適應度；ft為第t次迭代中的局部最優適應度。因為w取值在[1，2]的范圍內概率更大，所以大概率會選擇擴大收縮包圍圈，從而較好地解決了陷入局部最優的問題。其位置更新公式由式(12)變化為

X(t+1)=Xbest(t)+D2·ebl·cos(2πl)·w

(14)

2.4 隨機游動

隨機游動搜索機制是當前鯨魚個體Xi向著當前鯨魚種群中一個隨機個體Xrand(t)靠近來更新位置。雖然可能會偏離目標獵物，但是能夠增強全局搜索能力。該階段，系數向量|A|>1，位置更新模型如下：

一到冬天，要檢查幾次。不是怕別的，怕老鼠打了洞。葡萄窖里很暖和，老鼠愛往這里面鉆。它倒是暖和了，咱們的葡萄可就受了冷啦！

(15)

為了進一步增強算法的全局優化能力，引入了萊維飛行，其搜索步長的概率分布是有重尾分布的隨機行走，即具有大概率出現較大跨步的情況。其飛行步長s為

(16)

(17)

其中：Γ(x)為Gamma函數。因此改進后的位置更新公式為

(18)

其中：sign函數能取-1、0、1這3個值，代表著方向；常數ζ=0.01。

3 實驗與分析

3.1 實驗準備

此次實驗主要運用MATLAB強大的運算功能對采集的數據進行數據分析，并將結果可視化。數據的采集儀器為三坐標測量儀，如圖2所示。

圖2 運用三坐標測量儀對零件進行數據采集

實驗前對圓柱零件軸向等距采集10個截面，每個截面周向等距采集1 164個數據點。通過編程實現圓柱度的最小二乘評定(LSC)和雙包容評定(MZC)。為了測試混合策略改進的鯨魚優化算法(HWOA)在圓柱度誤差評定上的性能，設置對照組，除了鯨魚優化算法以外，再加入遺傳算法(GA)進行對比。

3.2 實驗步驟

以雙包容評定為例，給出改進鯨魚優化算法圓柱度誤差評定的步驟，其簡化流程如圖3所示。

圖3 算法流程

步驟1，給定算法的相關參數，設置算法的搜索空間為d=8，種群數量為n=100，最大迭代次數為T=500，變量的上下限ub、lb區間為[-30，30]。

步驟 2，利用式(9)生成初始種群，其中xn=rand(n，d)，再用式(4)計算初始種群中每個鯨魚個體的適應度值，并進行比較，得到初始最優個體Xbest(0)和初始最優適應度值。

步驟 3，開始迭代并更新鯨魚位置。在每一次迭代前首先更新參數p、a、A、C、l、w的值。判斷概率p和參數|A|的值，若p<0.5且|A|<1，則采用包圍收縮的方式更新種群位置，否則采用隨機游動的方式更新位置；若p≥0.5，則采用螺旋上升的方式更新位置。

步驟 4，再由式(4)計算更新位置后的鯨魚個體的適應度，并保存最優個體Xbest(t)和局部最優適應度。并判斷是否達到最大迭代次數，否則繼續迭代。

3.3 函數測試實驗

如表1所示，為了評估改進后算法相對于原始算法的性能，選擇2個可變維的基準函數來進行測試，包括一個單峰基準函數評估算法收斂速度和一個多峰基準函數評估算法全局搜索能力，且所有基準函數均有理論最優值(全局最小值)。

表1 基準測試函數

設定兩算法的種群規模和迭代次數保持一致，分別為100和500，算法維度設置3個檔次來進行對比，分別為50、100、200。對于每個基準函數，兩優化算法均獨立運行10次，計算結果的平均值和標準差，如表2所示，算法收斂曲線對比如圖4所示。

表2 不同維度下HWOA與WOA算法性能對比

圖4 不同維度下HWOA與WOA算法收斂曲線對比

在單峰函數中，由圖4(a)可以看出改進的算法具有較快的收斂速度，并且在求解Sphere函數時精度能比原始算法高出10個數量級。在多峰函數中，由圖4(b)可以看出，兩種算法精度相對變化不大，但改進的鯨魚優化相對于原始算法的收斂速度提升更加明顯，展現出其具有更強的跳出局部最優的能力。綜合來看，基于混合策略改進的鯨魚優化算法(HWOA)具有更快的收斂速度和全局搜索能力。綜合對比圖4中所有收斂曲線，可以看出在對基準函數不同維度的求解過程中，其收斂曲線波動范圍不大，展現出算法的穩定性。

3.4 實驗結果對比分析

基于雙包容評定，各優化算法對圓柱度誤差f的評定結果對比如表3所示。

表3 各算法雙包容評定結果對比

混合策略改進鯨魚優化算法評估結果及兩算法收斂速度對比如圖5—6所示。其中圖6為了使變化趨勢更加明顯，對y軸坐標進行取對數運算。

圖5 改進鯨魚優化算法評定結果

圖6 算法收斂速度曲線對比

分析表3可知：基于混合策略改進的鯨魚優化算法相對于傳統鯨魚算法在評定精度上有了進一步提升。由圖6可以看出：改進的鯨魚優化算法在第36次迭代時收斂，遺傳算法在第89次迭代時收斂，而鯨魚優化算法在第124次迭代時收斂，收斂速度提升較大；改進的鯨魚優化算法在算法迭代初期變化速度較快，后期變化速度較慢，說明非線性因子有效改善了算法的收斂效果。

為了對比算法的效率，在固定截面數的前提下，對不同算法引入時間函數，計算其運行時間，每個算法單獨運行5次取平均值，對比結果如表4所示。

表4 不同算法運行時間對比

分析表4可知：WOA算法改進前后運算時間基本無差別，因此改進算法引入的各個參數并不會增加算法的復雜度而影響運算時間；但改進后的算法相對于遺傳算法在運行效率上具有較大的優勢；最小二乘法運算效率最高，但該方法只是近似評定，不滿足最小條件準則，因此僅供參考。

表3中誤差數據為指定高度等間距采集10個截面所測得的結果。為了測試截面數量對誤差值的影響(以雙包容為例)，設定采樣高度在30～165 mm之間，同樣為等間距取樣，分別間隔60、45、30 mm，得到3、4、5個截面數下的誤差值如表5所示。

對比表3和表5數據可以發現：HWOA、WOA、GA、LSC運算出來的結果伴隨著截面的變化具有略微的波動，但影響不是特別大，且具有略微上升的現象。這是因為隨著采樣截面不斷增加，其采樣結果越來越逼近真實圓柱零件，使得圓柱度誤差越來越接近真實值。由各算法間對比可以看出：改進后的鯨魚優化算法，在精度上具有一定的優勢，不同截面數下的誤差值均相對較小。

為驗證在單包容評定中是否也會出現這種趨勢(以MCC為例)，同樣設定采樣高度在30～165 mm之間，采樣間隔為60、45、30、15 mm，得到3、4、5、10個截面數下的誤差值如表6所示。

表6中各算法評定結果隨著截面數的變化曲線與最小二乘(LSC)算法的變化曲線如圖7所示。

從圖7可以看出：在單包容評定下也同樣具有略微上升的趨勢，且各自的變化波動也較小。

4 結論

在鯨魚優化算法的基礎上引入Tent混沌映射、非線性參數、自適應權重系數和萊維飛行，來改進鯨魚優化算法的不足。通過基準函數測試，證明基于混合策略改進的鯨魚優化算法具有更快的收斂速度，算法的搜索能力也有了提高。經過實驗對比，相比基于GA、WOA算法的圓柱度誤差評定方法，改進后的鯨魚優化算法在精度上優于其他3種對比方法，評定效率也具有顯著優勢。

基于混合策略改進的鯨魚優化算法，原理簡單明了，算法編程也不復雜，局部以及全局搜索能力有了進一步提升，應用場景也比較廣泛，可以推廣至多種問題的求解中。