基于子域法的永磁體周向分段式轉子渦流損耗解析模型

尹宏乾

（國華諸城風力發電有限公司，山東諸城 262200）

0 引言

高速永磁電機因其具有高效率、高功率密度、高穩定性等優點，在航空航天發電機、高速磨床等方面具有廣闊的前景[1-3]。永磁電機需要變頻器變頻起動，變頻器輸出的電流波形中包含大量諧波，使得電機磁場中諧波含量增加，電機損耗增大，會引起轉子溫度升高，達到永磁體退磁溫度點，使其發生不可逆失磁風險，影響電機運行的可靠性。因此高速永磁電機的設計，需要快速準確計算轉子渦流損耗，避免永磁體失磁。

為了提高高速永磁電機的運行可靠性，許多文獻采用有限元法對轉子渦流損耗的抑制方式進行了研究。文獻[4-6]通過采用定子齒上開輔助槽的方法降低轉子渦流損耗。文獻[7]通過改變極槽配合，繞組形式等方式減小諧波含量，以此來抑制轉子渦流損耗。此外，優化護套形狀，在護套表面進行徑向和周向開槽來阻斷渦流流通路徑，或采用新型轉子護套結構等都能起到抑制轉子渦流損耗的作用[8-9]。然而，護套開槽后機械強度并不能得到保證，并且在很大程度上增加了制造難度。永磁體分段是減小轉子渦流損耗的常用方法。分段后永磁體內的渦流路徑被分割成更小的回路，增加了等效電阻[10]，從而降低永磁體渦流損耗，同時永磁體分段對電機性能影響較小[11-13]。有限元法雖然能夠考慮諸多影響因素，有著較高的計算精度，但并不利于電機的初始優化設計。例如，采用永磁體分段減小轉子渦流損耗時，為確定合適的分段數量，需要建立具有不同分段數的仿真模型，建模過程較為繁瑣且計算時間較長。而解析法則在電機初始設計中具有計算效率高的優勢，并且能夠給予一定的理論分析。

目前，已經有大量的解析模型被用來計算轉子渦流損耗，主要分為二維或三維解析模型。三維解析模型能夠考慮永磁體中渦流的三維分布，計算永磁體不同方向分段對轉子渦流損耗的影響。文獻[14]提出一種考慮渦流反作用影響的準三維分析方法，但忽略了定子開槽的影響。文獻[15-16]分別采用廣義圖像理論和精確子域方法，建立三維轉子渦流損耗的解析模型，但模型過于復雜，應用還不成熟。二維解析模型應用則較為廣泛，較早階段，為方便計算，解析模型通常將定子三相繞組等效為電流片計算低速時的轉子渦流損耗[17-18]。文獻[19]利用該方法計算了永磁體分段后的渦流損耗值。這種方法計算簡單，但忽略了定子開槽和高頻時永磁體中渦流反作用的影響，對于高速電機的設計會造成較大誤差。文獻[20]考慮了趨膚效應對永磁體分段的影響，確定永磁體分段異常的參數范圍。然而，該方法只對主要次數諧波造成的損耗進行計算且忽略了定子開槽的影響。為準確考慮定子開槽影響，文獻[21-22]分別采用磁導函數和精確子域方法，計算了轉子渦流損耗，而后者并未考慮渦流反作用的影響。文獻[23]針對永磁體產生的永磁磁場，引入擴散方程，考慮定子開槽和渦流反作用的影響。文獻[24]為考慮渦流反作用影響，采用了考慮導體中渦流的擴散方程，計算了負載磁場下的渦流損耗，但是沒有考慮護套及電流時間諧波，文獻[25]在其基礎上進一步考慮電流時間諧波的影響。然而，上述考慮渦流反作用影響的擴散方程，由于方程解析式中存在沒有顯式積分形式的貝塞爾函數，因而，無法使得每段永磁體橫截面渦流為零[26]。這就意味著，該方法無法應用于永磁體分段的永磁電機中。綜上所述，目前尚且缺少針對高速永磁電機永磁體分段情況下考慮渦流反作用的轉子渦流損耗解析模型。

本文的主要貢獻是基于子域法提出了一種針對永磁體周向分段高速永磁電機轉子渦流損耗解析模型。該模型利用磁導函數，引入考慮各次諧波透入深度的衰減系數來考慮定子開槽和渦流反作用的影響。基于該解析模型，對永磁體不同分段數的轉子渦流損耗進行分析。將永磁體分段后的轉子渦流損耗解析及有限元結果對比，證明了該解析模型具有較高的計算精度。

1 模型簡述

1.1 結構與參數

本文建立了三層子域模型，計算永磁體周向分段的高速永磁同步電機轉子渦流損耗。圖1 為永磁體周向分段的子域模型。

圖1 永磁體周向分段的高速永磁電機子域模型

為便于推導轉子渦流損耗解析解，作如下假設：

1） 假設定轉子鐵芯的磁導率無窮大，忽略鐵芯飽和影響；

2） 三相繞組采用等效電流片表示；

3） 護套為不導磁材料，護套和永磁體材料各向同性，磁導率及電導率為常數；

4）不考慮轉子鐵心的損耗。

在圖1 中，Rsl，Rpm，Rr分別為護套外半徑，永磁體外半徑以及轉子軛外半徑。Rg是定子內半徑。

本文以一臺20 kW，20 000 r/min，4 極18槽高速永磁電機為例進行分析。該電機定子鐵芯材料為硅鋼片，永磁材料采用極弧系數為1的燒結釹鐵硼，同時護套采用材料為碳纖維，其主要參數見表1。

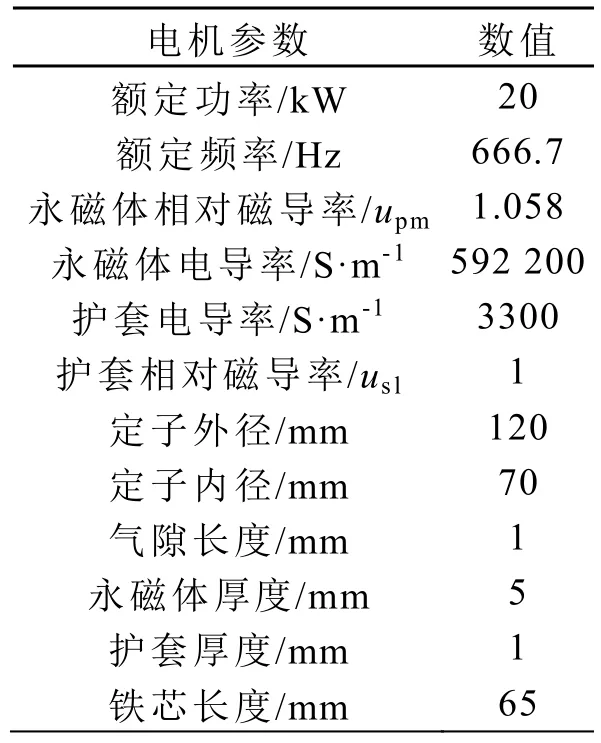
表1 電機主要參數

永磁體周向分段的高速永磁電機轉子渦流損耗解析模型流程圖如圖2 所示。其中包括的過程有：

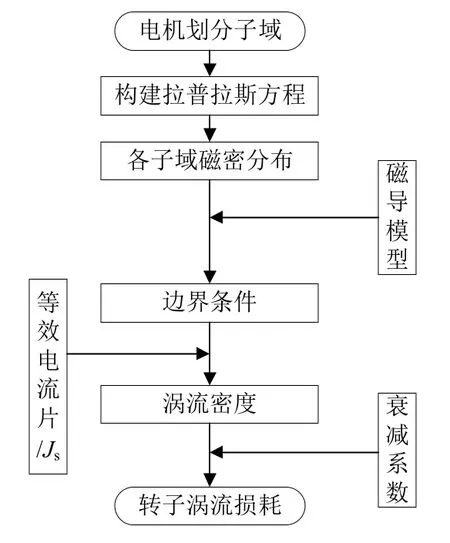
圖2 解析流程圖

1）建立僅考慮電樞磁場時的氣隙、護套以及永磁體子域的拉普拉斯方程并求解各部分磁密；

2）通過引入磁導模型考慮定子開槽影響，并求解各子域的渦流密度；

3）為考慮渦流反作用影響引入衰減系數計算轉子渦流損耗。

1.2 損耗計算

忽略渦流反作用時，導體中的渦流密度表達式為[22]:

式中，σy為相應子域的電導率。Ay1代表各子域失量磁位表達式，具體求解過程見附錄。

公式（1）中的第二項存在是因為當永磁體進行分段后，每段永磁體會形成一個單獨的渦流回路，需要通過解析公式強制每段永磁體橫截面上的渦流為零。若對于護套子域，該項為零。C(t)公式為：

為了考慮定子開槽對轉子渦流損耗的影響，通過引入磁導模型對各子域的磁通密度進行修正：

其中，l1為磁導諧波次數，kg為氣隙系數。

對于高速永磁電機，高頻諧波磁場在轉子中產生的渦流會對諧波磁場造成影響，又由于永磁體分段后無法采用貝塞爾函數來考慮渦流反作用[26]，因此本文引入透入深度δm 進行分析：

式中，ωm為m次諧波角頻率，μ0為真空磁導率。

不同厚度h處渦流衰減系數為：

由于渦流衰減隨厚度方向的變化是連續的，不同次數的諧波磁場透入深度不同，因而利用公式（6）計算得到各次諧波磁場在轉子導體中的平均渦流密度，從而考慮集膚效應對渦流沿厚度方向分布不均的影響。

式中，Jb為導體表面渦流密度，Δh為各次磁場諧波在導體中的透入深度，其值與δm 相等。

有一種叫“竽”的樂器，外形和笙極為相似，容易讓人混淆。其實它們的差別的確不大，都屬于匏類樂器，只是竽比笙大，管數也比較多。

由平均渦流密度計算得到一個電周期內轉子各部分渦流損耗計算表達式為：

式中，T為電周期，V為導體體積。

2 有限元驗證及分析

電機采用PWM 供電，圖3 為電機輸入電流波形。為了驗證解析模型的適用性，本文建立二維有限元模型。有限元模型網格如圖4 所示。

圖3 電流波形

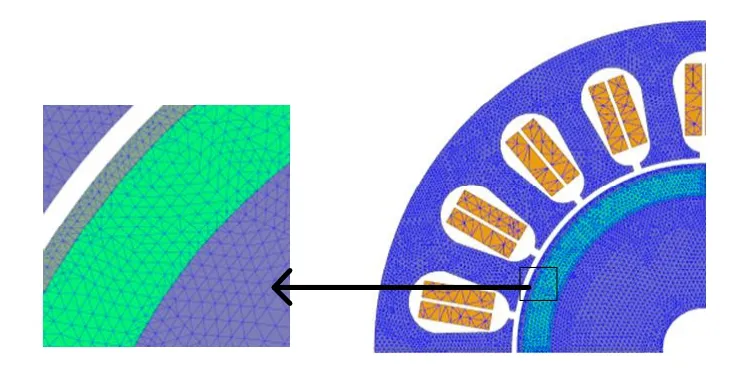
圖4 有限元網格劃分

圖5 給出了永磁體未分段時的轉子各部分渦流損耗結果，可以看出由于碳纖維材料電導率較低，護套產生的渦流損耗較少，轉子渦流損耗主要集中于永磁體中。本文所建立的考慮渦流反作用的解析模型與有限元結果相比，計算誤差為5.5%。當令衰減系數λ1 設為1 時，即不考慮永磁體渦流反作用，可以看出轉子渦流損耗增加45%，因此，高速永磁電機在高頻時需考慮渦流反作用的影響，否則會產生極大誤差。

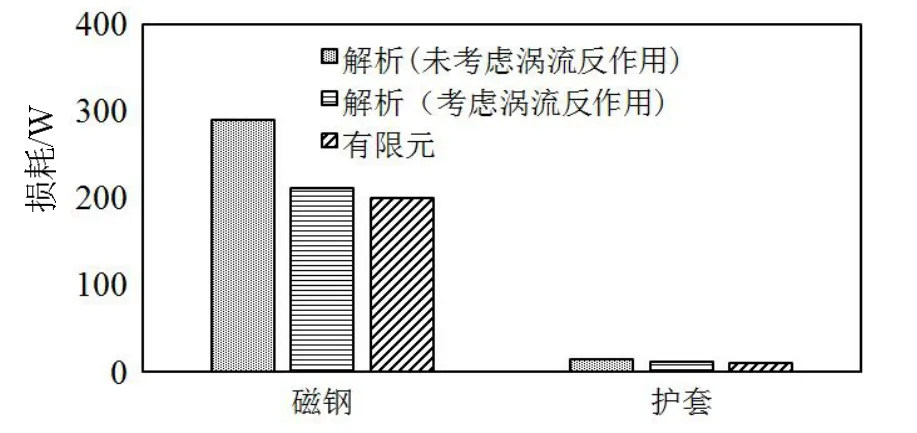
圖5 額定頻率時護套及永磁體的渦流損耗

圖6 給出了護套和永磁體渦流損耗隨永磁體分段數的變化規律，從圖中可以看出，隨永磁體分段數增加，永磁體渦流損耗呈先增后減的變化規律，這與忽略渦流反作用的解析模型變化規律不同[17]。隨著永磁體分段數增加，渦流由電感限制型變為電阻限制型[14]，故渦流損耗先增加后減少。

圖6 護套及永磁體渦流損耗隨永磁體分段數的變化

永磁體分段不僅影響了自身渦流損耗的變化，同時也會影響護套渦流損耗，使其有所增加。但對于解析模型，由于未考慮永磁體分段對護套渦流損耗的影響，使得護套渦流損耗計算結果保持不變，這也是解析與有限元計算結果存在誤差的原因。雖然護套渦流損耗增加，但增加幅度較小，僅變化了4W 左右，相比于永磁體渦流損耗，其占比較小，對轉子總渦流損耗的整體變化趨勢影響不大。因而，解析模型還是具備著較高的計算精度。

由于護套渦流損耗對總損耗的影響不大，為此，本文主要針對永磁體渦流損耗變化規律進行研究。在圖6 基礎上，給出了與忽略渦流反作用的解析結果對比，如圖7 所示。從圖中可以看出，忽略渦流反作用的解析結果是隨著永磁體分段數的增加而減小，這與考慮渦流反作用的解析結果規律不同。當永磁體分段數在3 段以下時，考慮渦流反作用與忽略渦流反作用的解析結果間存在較大差距，而當分段數在3 段以上時，兩者之間的差距較小，這說明隨著永磁體分段數的增加，渦流反作用對永磁體渦流損耗的影響減弱。因此，對于高速永磁電機，隨著永磁體分段數的增加，永磁體渦流損耗存在上升趨勢，是由于渦流反作用的影響。

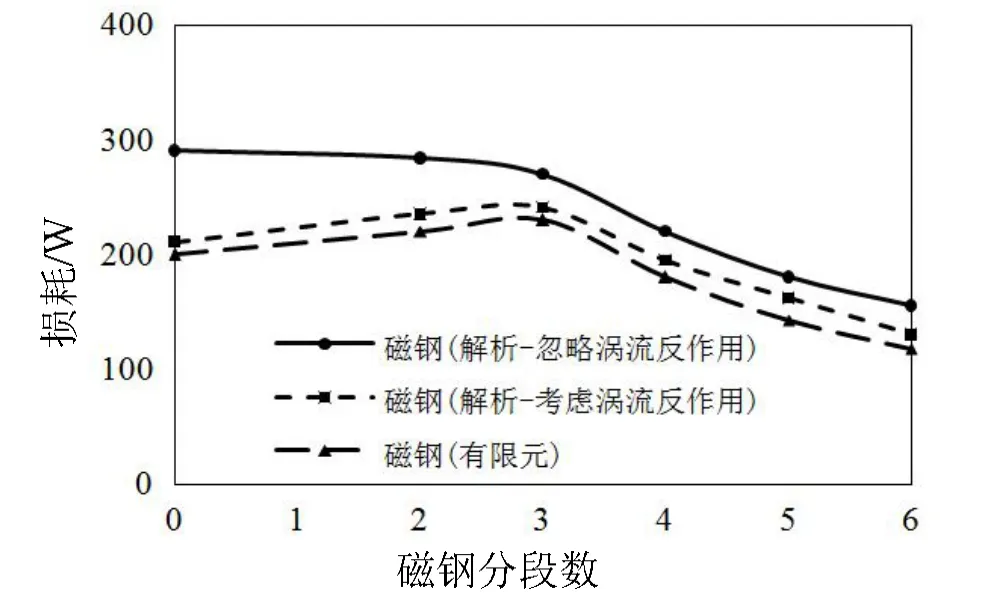
圖7 不同解析模型下永磁體渦流損耗對比

為了說明上述觀點，通過有限元仿真得到永磁體中渦流分布，如圖8 所示。當永磁體不分段時，受渦流反作用影響，渦流大多集中于永磁體表面，隨著分段數的增加，渦流逐漸遍布于整個永磁體中，永磁體損耗也增加，當分段數達到一定程度時，由于等效阻抗的增加[10]，損耗開始減小，起到減小損耗的作用。

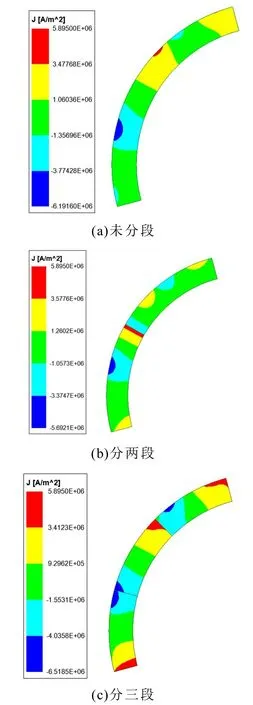
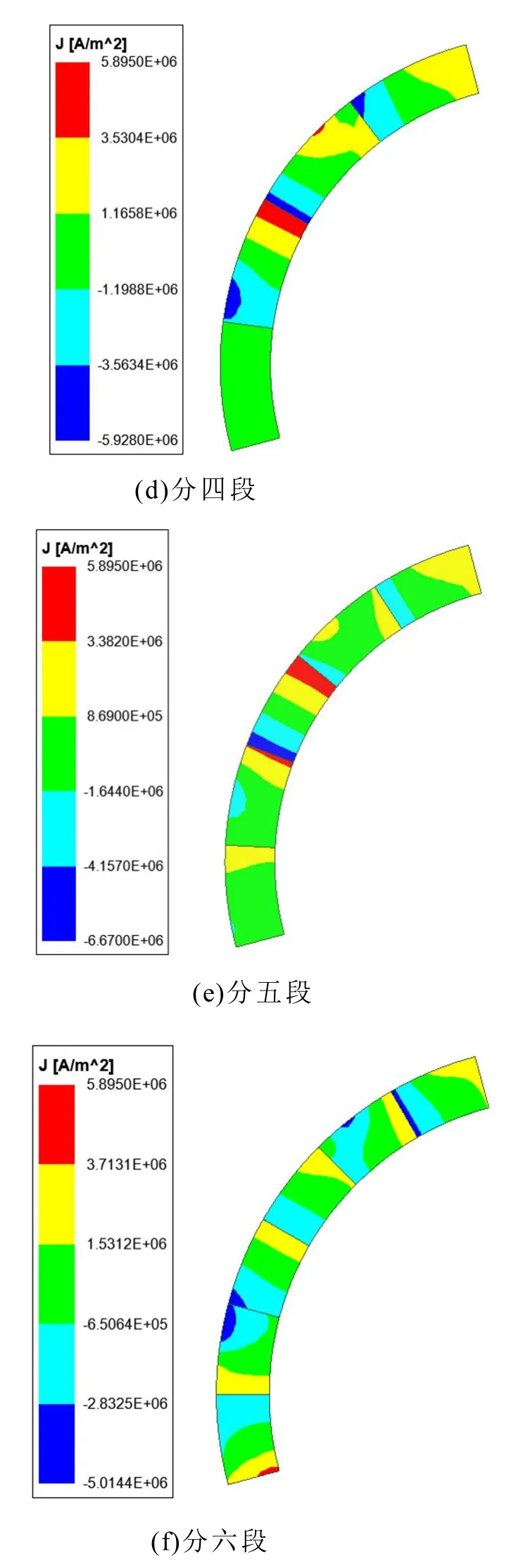
圖8 永磁體渦流分布

3 結論

本文基于子域法，通過對永磁體進行周向分段，建立了一個帶有護套的高速永磁電機永磁體周向分段轉子渦流損耗解析模型，并給出了詳細的計算過程。該模型通過采用磁導模型考慮定子開槽對磁場影響，引入衰減系數來考慮渦流反作用影響，有效地提高了計算精度。得到了電樞磁場中永磁體分段后的渦流損耗變化規律，并將解析結果與有限元仿真結果進行了比較，驗證了解析模型的準確性。