密度矩陣泛函理論及其計(jì)算方法

2024-03-15 09:55:52IRIMIAMarinela

湖州師范學(xué)院學(xué)報(bào) 2024年2期

關(guān)鍵詞：理論方法

IRIMIA Marinela,王堅(jiān)

(1.湖州師范學(xué)院國際學(xué)院,浙江湖州 313000; 2.湖州師范學(xué)院理學(xué)院,浙江湖州 313000)

0 引言

客觀世界是由原子和分子組成的,它們遵從量子力學(xué)的規(guī)律.因此,原則上只要求解量子力學(xué)方程,就可以知道材料的各種物理化學(xué)性能.與實(shí)驗(yàn)比較,求解量子力學(xué)方程的計(jì)算成本輕,因此其已成為材料設(shè)計(jì)的重要手段.

一般的原子、分子和固體系統(tǒng),其物理性質(zhì)可通過求解下面的量子力學(xué)方程,即薛定諤方程來求解：

HΨ=EΨ.

采用原子單位,哈密頓算符H由以下幾部分組成：

其中,第一項(xiàng)是電子的動能算符,第二項(xiàng)是原子核與電子間的庫侖吸引勢能,第三項(xiàng)是電子間的庫侖排斥勢能,第四項(xiàng)是原子核間的庫侖排斥勢能.假定波恩-奧本海默近似成立,即在考慮電子運(yùn)動時(shí),原子核可以看作是靜止的,其原因是核比電子的質(zhì)量大得多.對只有一個(gè)電子的氫原子,這一方程可以嚴(yán)格求解,且解的結(jié)果已被光譜實(shí)驗(yàn)完全證實(shí),由此奠定了量子力學(xué)的基礎(chǔ).

對由兩個(gè)電子或更多電子組成的原子、分子和固體系統(tǒng),這個(gè)方程無法嚴(yán)格求解,只能通過近似方法求解.因?yàn)殡娮邮琴M(fèi)米子,波函數(shù)對于任意兩個(gè)電子交換要具有反對稱性.為滿足這一性質(zhì),波函數(shù)Ψ可采用行列式的形式,因?yàn)樾辛惺降膬尚谢騼闪薪粨Q后,行列式值就變符號,正好符合反對稱性要求.最簡單的波函數(shù)形式是用一個(gè)行列式來表達(dá)的,這種方法也稱為Hartree-Fock方法.為提高精確度,可采用多個(gè)行列式的線性組合來近似波函數(shù),這種方法稱為組態(tài)相互作用(簡稱CI).一個(gè)行列式對應(yīng)一個(gè)組態(tài),因此這是一種多組態(tài)的波函數(shù)方法.這在理論上是理想的,但隨著電子數(shù)目的增加,行列式數(shù)目成指數(shù)式增加,因此這種方法很難推廣到多電子系統(tǒng).

20世紀(jì)50年代,人們認(rèn)識到計(jì)算系統(tǒng)的能量不需要波函數(shù)的全部信息,只需要密度矩陣.例如,一階密度矩陣的定義是[1]：

它是除了第一個(gè)電子的坐標(biāo)外,對其余電子的坐標(biāo)進(jìn)行積分后得到的結(jié)果.每個(gè)電子有3個(gè)空間坐標(biāo)和1個(gè)自旋坐標(biāo),積分包含空間坐標(biāo)的積分和自旋坐標(biāo)的求和.根據(jù)定義,它是厄米矩陣,因此可以對角化,本征值為實(shí)數(shù),

其中,本征函數(shù)χi稱為“自然軌道”;本征值λi稱為自然軌道χi的占有數(shù),0≤λi≤1.

因?yàn)殡娮邮侨Ｗ?只要知道一個(gè)電子的動能,總動能就等于它的N倍.利用一階密度矩陣,電子的動能可以簡化為：

同樣,原子核與電子的庫侖吸引勢能也可簡化為單個(gè)電子的積分：

這里的γ(1,1)是γ(1′,1)的對角元,稱為電子密度.

我們還可以定義二階密度矩陣(或電子對密度)：

它是波函數(shù)和它的復(fù)共軛中除了第一和第二個(gè)電子的坐標(biāo)外,對其余電子的坐標(biāo)進(jìn)行積分后剩下的結(jié)果.其中,N(N-1)是電子對的總數(shù)目.電子間的庫侖勢能是兩體算符,利用電子的全同性,只要考慮一對電子的庫侖勢能,然后乘上電子對總數(shù)即可,因此可以用Γ(1,2)來表示,即：

綜上所述,與電子相關(guān)的能量可以用密度矩陣表示為：

因此,只要知道相當(dāng)于密度矩陣γ(1′,1)和Γ(1,2)的信息,而不需要波函數(shù)的全部信息,就可以獲得電子系統(tǒng)的能量.

1964年,Kohn和Hohenberg提出了密度泛函理論(簡稱DFT)[2].他們用反證法證明電子系統(tǒng)基態(tài)的能量是電子密度的泛函.然而這一定理只是個(gè)存在性證明,這個(gè)密度泛函的具體表達(dá)形式仍然未知.按照上面的分析,得出表1所示的結(jié)果.只有原子核與電子的庫侖吸引勢能可以用密度表達(dá),電子能量的其余兩項(xiàng)都不能用密度嚴(yán)格表達(dá),所以只能尋找近似模型.Kohn和Sham最早通過均勻電子氣體模型給出了一個(gè)稱為“局域密度近似(LDA)”的泛函模型[3].固體中的電子運(yùn)動近似均勻電子氣體,因此這個(gè)模型在固體物理領(lǐng)域最先得到應(yīng)用.但原子或分子中的電子密度一般是不均勻的,因此20世紀(jì)90年代,Perdew等對密度不均勻體系提出了“廣義梯度近似”模型[4].DFT才開始在原子分子物理和化學(xué)領(lǐng)域得到應(yīng)用.

表1 密度泛函方法與密度矩陣泛函方法的比較

1975年,Gilbert提出了密度矩陣泛函理論[5],這種理論用一階密度矩陣作為泛函變量.與DFT方法比較,這一方法的優(yōu)點(diǎn)是電子動能,以及原子核與電子的庫侖勢能都可以用一階密度矩陣嚴(yán)格表達(dá),只有電子間的庫侖勢能需要尋找泛函模型.密度矩陣泛函方法與密度泛函方法的比較見表1.從泛函模擬的角度看,這種理論方法比DFT更有希望.因此不少DFT學(xué)者,如M Levy、E K U Gross、E J Baerends等,都成為密度矩陣泛函理論的倡導(dǎo)者.

1 密度矩陣泛函

用CI波函數(shù)展開Γ(1,2),電子間的庫侖勢能可表示為：

其中,〈ij|kl〉為雙電子積分.在波函數(shù)方法中,Γij,kl與軌道指標(biāo)ij和kl所在的行列式的波函數(shù)展開系數(shù)有關(guān).在密度矩陣泛函理論中,自變量是一階密度矩陣,包括自然軌道χi及其占有數(shù)λi,因此原則上Γij,kl是自然軌道和占有數(shù)的函數(shù).Γij,kl有4個(gè)下標(biāo),每個(gè)下標(biāo)有M個(gè)軌道選項(xiàng),因此Γij,kl共有M4項(xiàng).如果軌道數(shù)M=10,那么就有1萬個(gè)關(guān)于Γij,kl的泛函,這么多泛函逐個(gè)落實(shí)是不現(xiàn)實(shí)的.為使計(jì)算可行,泛函設(shè)計(jì)時(shí)常作近似處理,一般只保留指標(biāo)為Γij,ij和Γij,ji的項(xiàng),而忽略其他指標(biāo)項(xiàng),文獻(xiàn)[6]中把這種泛函模型稱為“JK”型.原本Γij,kl有M4項(xiàng),實(shí)際模擬的只有M2項(xiàng).

同時(shí),由于雙電子積分〈ij|kl〉已包含軌道,所以在設(shè)計(jì)Γij,kl的泛函模型時(shí)往往忽略軌道變量,而是假定Γij,kl只與占有數(shù)λi有關(guān),這種簡化的泛函模型稱為“代數(shù)型”[7].

對實(shí)際的分子,我們用波函數(shù)推導(dǎo)的電子對密度對文獻(xiàn)中發(fā)表的密度矩陣泛函進(jìn)行逐項(xiàng)比較.結(jié)果發(fā)現(xiàn),“JK”型和“代數(shù)型”泛函都不能重復(fù)從波函數(shù)得到Γij,kl,它們不具有一一對應(yīng)的關(guān)系.這說明這些泛函模型都存在唯一性、對稱性和普適性問題[7-8].

為了克服這些問題,經(jīng)過長期的摸索,我們對以下形式的Γ(1,2)分解專門進(jìn)行研究：

Γ(1,2)=γ(1,1)γ(2,2)-γ(1,2)γ(2,1)+λ(1,2),

其中,第一項(xiàng)是獨(dú)立粒子引起的電子對密度,第二項(xiàng)是交換效應(yīng).這兩項(xiàng)都可用一階密度矩陣表達(dá).后一項(xiàng)λ(1,2)稱為“cumulant”,其對應(yīng)的電子能量為：

著名DFT學(xué)者M(jìn) Levy把Ecum稱為密度矩陣泛函理論的關(guān)聯(lián)能,它是能量泛函中唯一需要用泛函模擬的部分.因?yàn)殛P(guān)聯(lián)能使能量降低,所以Ecum總是取負(fù)數(shù).對Ecum進(jìn)行模擬可避免模擬Γij,kl時(shí)符號的不確定性.這個(gè)符號的不確定性問題,文獻(xiàn)中稱為“phase dillema”[9].通過積分,Ecum隱含了所有可能指標(biāo)ij,kl引起的貢獻(xiàn),避免了“JK”型和“代數(shù)型”泛函的近似性,也避免了模擬Γij,kl時(shí)有M4項(xiàng)之多的麻煩.

信息論之父Shannon曾提出,“信息熵”函數(shù)S=-∑ipilogpi可用來描述統(tǒng)計(jì)分布pi.我們將占有數(shù)分布λi看作一個(gè)統(tǒng)計(jì)分布,用S=-∑iλilogλi作為與這個(gè)分布相聯(lián)系的信息熵,發(fā)現(xiàn)這個(gè)熵函數(shù)與關(guān)聯(lián)能Ecum有較好的線性關(guān)系[10]：

Ecum=-κS-b,

其中,κ和b是與系統(tǒng)有關(guān)的常數(shù),可以通過結(jié)合能、鍵長等理論或?qū)嶒?yàn)數(shù)據(jù)來擬合.按照這一表達(dá)式,當(dāng)熵取最大值時(shí),關(guān)聯(lián)能達(dá)到最小值.關(guān)聯(lián)能越低,意味著系統(tǒng)越穩(wěn)定,這正是我們期望的,也是符合物理要求的.考慮到電子是費(fèi)米子,應(yīng)符合狄拉克-費(fèi)米統(tǒng)計(jì),信息熵的嚴(yán)格表達(dá)形式應(yīng)為：

S=-∑i[λilogλi+(1-λi)log(1-λi)].

2 自洽場方程

Gilbert在提出密度矩陣泛函理論時(shí),發(fā)現(xiàn)當(dāng)占有數(shù)λi為分?jǐn)?shù)時(shí),軌道能級都是簡并的[5].這一結(jié)果與實(shí)驗(yàn)或DFT計(jì)算的結(jié)果不符,他在文章中表示意外.因?yàn)槟芗壓啿?無法獲得DFT那樣的Kohn-Sham方程,計(jì)算時(shí)只能依靠非線性優(yōu)化方法,計(jì)算效率很低.這一問題成為密度矩陣泛函理論的一個(gè)歷史性問題.

用信息熵表達(dá)關(guān)聯(lián)能后,系統(tǒng)的電子能量可表示為：

E=∑iλihii+Y-κS-b,

其中,與單電子有關(guān)的能量,hii=〈χi|h|χi〉,包括動能以及原子核對電子的庫侖吸引勢能,單電子算符h的定義為：

第二項(xiàng)Y包含雙電子能量中可以用一階密度矩陣表達(dá)的部分：

其中,

稱為雙電子積分.

考慮到自然軌道的正交歸一性,以及占有數(shù)的求和性質(zhì)∑iλi=N,我們用拉格朗日函數(shù)方法構(gòu)造一個(gè)無條件優(yōu)化的變分函數(shù)：

其中,μ和Λij是拉格朗日因子.

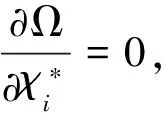
其中,算子Jj和Kj與Hartree-Fock方法中定義的庫侖算子和交換算子完全一樣,

為簡化書寫,定義算子：

這個(gè)算子與Hartree-Fock方法中的Fock算子比較,只多了系數(shù)λj.

(λi-λj)〈j|f|i〉=0.

若使這個(gè)方程成立,則f|i>應(yīng)具有本征方程的形式,即：

fχi(1)=iχi(1).

〈i|f|i〉+κ[logλi-log(1-λi)]=μ.

利用〈i|f|i〉=i,可以解得：

編寫量子力學(xué)計(jì)算軟件是一項(xiàng)長期積累的工作.因?yàn)楸疚牡谋菊髦捣匠掏琀artree-Fock方程非常接近,所以我們可以把Hartree-Fock程序作為出發(fā)點(diǎn)來開展研究.Hartree-Fock程序已研發(fā)了90多年,文獻(xiàn)資料相當(dāng)豐富,程序代碼也很多,如原子的高斯基函數(shù)庫、雙電子積分、矩陣對角化等方面的內(nèi)容.利用這些文獻(xiàn)資料,可以大大加快新方法計(jì)算程序的編寫.

Hartree-Fock方法是一個(gè)非常有效、穩(wěn)定的計(jì)算方法.由于本征值方程的相似性,本方法也具有相當(dāng)?shù)姆€(wěn)定性、可靠性和可行性.在自洽場收斂方面,本文的方法比Hartree-Fock方法或DFT的Kohn-Sham方程更有優(yōu)勢,其原因是軌道占有數(shù)可連續(xù)變化,而在Hartree-Fock方法或Kohn-Sham方法中,占有數(shù)是跳躍性的,從1變成0或從0變成1,這容易使自洽場在收斂過程中,在近乎簡并的軌道上發(fā)生跳躍,從而出現(xiàn)振蕩現(xiàn)象而難于收斂.

3 計(jì)算舉例：氫分子的分解

氫分子的分解問題是密度泛函理論的一個(gè)弱點(diǎn),楊偉濤等曾專門在Science雜志上討論這個(gè)問題[12].在DFT計(jì)算中,密度用軌道來展開,軌道上填充電子的方式按能級由低到高的次序來填充,有電子占據(jù)的軌道,占有數(shù)為1,否則為0.這一填充規(guī)則與Hartree-Fock方法一致,相當(dāng)于用單個(gè)行列式表達(dá)波函數(shù).在波函數(shù)計(jì)算領(lǐng)域,人們早就知道,單個(gè)行列式不能描述具有靜態(tài)關(guān)聯(lián)的系統(tǒng),比如遠(yuǎn)離平衡態(tài)的氫分子.

圖1為利用不同方法計(jì)算的氫分子能量隨原子間距變化的結(jié)果.當(dāng)氫分子分解成兩個(gè)氫原子后,能量等于兩個(gè)氫原子的能量之和,每個(gè)氫原子的能量是-0.5個(gè)原子單位,所以總能量應(yīng)趨向于-1.由圖1可知,Hartree-Fock(HF)方法、DFT的LDA泛函方法都沒有收斂到正確的結(jié)果(-1),而本文的方法和CI方法都給出了正確的結(jié)果.因?yàn)樵诿芏染仃嚪汉碚撝?軌道占有數(shù)λi可以為分?jǐn)?shù),這與CI波函數(shù)方法一樣,所以它們的結(jié)果一致.這一結(jié)果說明,占有數(shù)可以為分?jǐn)?shù),密度矩陣泛函理論是一個(gè)比DFT方法更靈活、更完美、更精確的理論方法.對于四個(gè)氫原子組成的正方形結(jié)構(gòu)和50個(gè)氫原子組成的一維分子鏈,我們也獲得了類似的結(jié)果[13].

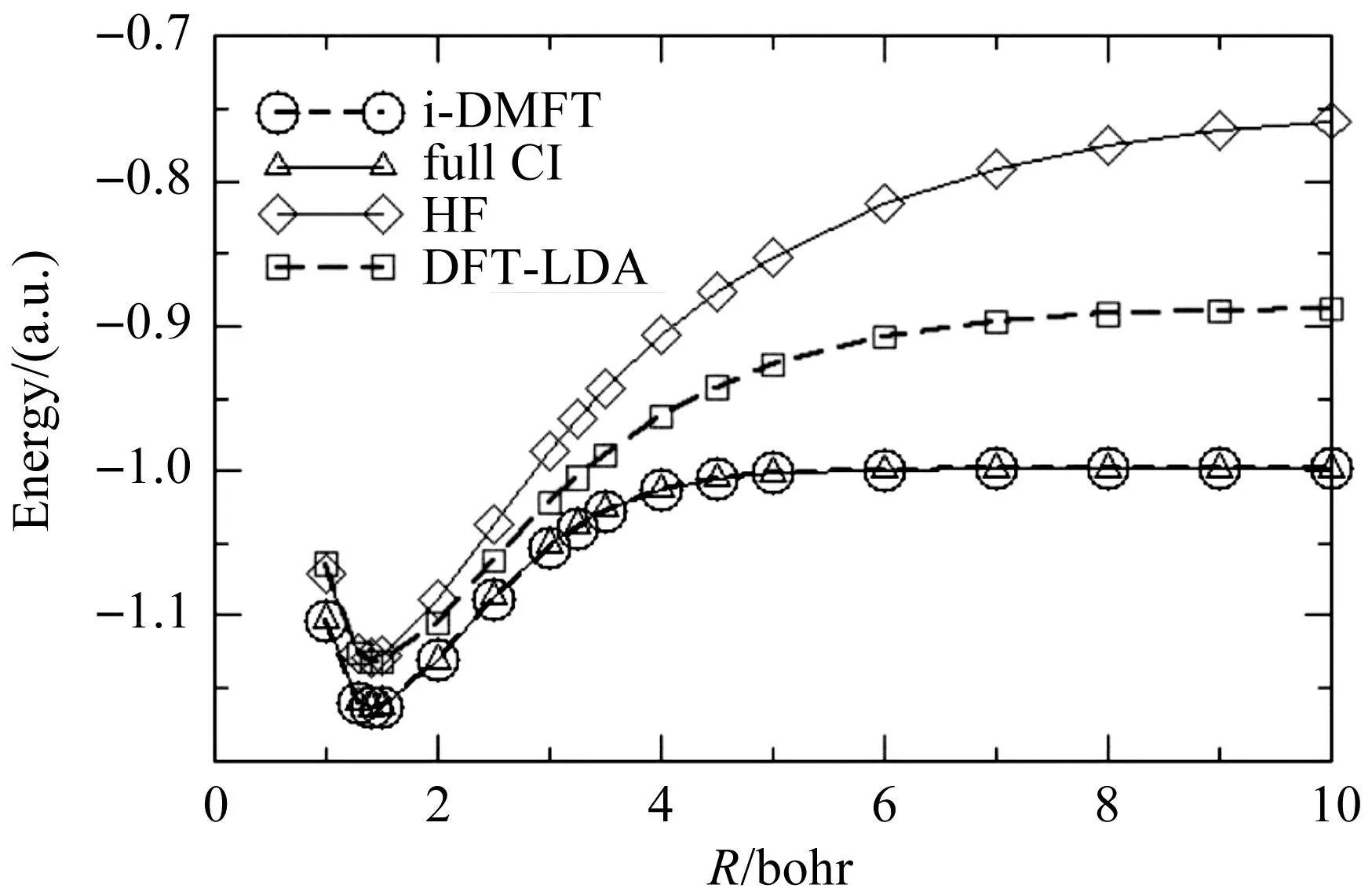
圖1 氫分子分解過程的能量曲線

4 結(jié) 語