基于特征變量擴展的含氣飽和度隨機森林預測方法

桂金詠，李勝軍，高建虎，劉炳楊，郭 欣

（中國石油勘探開發研究院西北分院，蘭州 730020）

0 引言

含氣飽和度是天然氣藏商業價值評估、儲量提交、井位優選、剩余氣描述等定量化分析工作的重要物性參數，可以直接通過試氣數據或使用測井曲線解釋得到。目前，在地球物理勘探領域已經提出了大量含氣飽和度測井解釋方法，但有關含氣飽和度的地震解釋方法卻較少［1-3］。利用地震數據預測天然氣藏的含氣飽和度是一種復雜的、多解性的以及高度非線性的地震反演問題，現有的試圖從地震信息中解譯出含氣飽和度信息的方法，大多都是借助疊前地震反演技術先從疊前地震數據中反演出彈性參數數據，繼而重點研究如何更高精度地將彈性參數數據進一步反演為含氣飽和度等物性參數，而物性參數與彈性參數間的巖石物理模型則起到一種正、反演基本準則的作用。Bachrach［4］以經典的Gassmann 方程為基礎，建立了縱波阻抗、橫波阻抗及密度與孔隙度、飽和度等物性參數間的統計巖石物理模型，實現了孔隙度和飽和度的聯合反演。胡華鋒［5］結合統計巖石物理模型與貝葉斯分類器，對儲層物性參數進行了反演。De Figueiredo 等［6］利用混合高斯模型獲取物性參數的先驗分布概率密度函數，提出了貝葉斯線性解析化物性參數反演方法。劉興業等［7］針對統計巖石物理反演中似然函數難以表征的問題，采用核估計的方法得到了條件概率密度函數，基于核貝葉斯判別法預測物性參數。李紅兵等［8］提出了一種基于彈性阻抗的、適用于復雜孔隙儲層孔隙結構的飽和度反演方法。另外，為了避免地震數據到彈性參數數據，再到物性參數數據這種“兩步”反演方法誤差傳遞的問題，也有學者嘗試將巖石物理模型與Zoeppritze 地震反射方程或其簡化方程相融合，提出了物性參數地震直接反演方法，直接將疊前地震數據反演為含氣飽和度、孔隙度等物性參數數據。桂金詠等［9］結合包裹體巖石物理模型將雙相介質地震反射系數推導成含氣飽和度、孔隙度和泥質含量的函數，并對其應用差分進化算法求解。Lang 等［10］在Gassmann 方程的基礎上，結合臨界孔隙度模型，推導了流體體積模量、剪切模量及密度隨巖石基質、流體參數的偏導數，發展了基于貝葉斯線性反演的疊前地震AVO 物性預測。Liu 等［11］基于Kuster-Toks?z 巖石物理模型推導了飽和巖石模量的線性近似式，采用基于柯西約束的貝葉斯最大后驗概率解，開展了疊前地震確定性物性參數反演。李坤等［12］推導了利用KT 巖石物理模型高階近似和Gray 地震反射模型表征的疊前地震AVO 反射系數方程，假設在待反演物性參數服從混合概率先驗模型的前提下，直接反演出孔隙度、飽和度及泥質含量。Fjeldstad 等［13］利用高斯混合模型表示含氣飽和度等物性參數的先驗分布特征，結合地質統計學空間模擬技術，提出了含氣飽和度的“一步法”地質統計學反演。

實際上，無論是“兩步法”還是“一步法”都離不開巖石物理建模過程。對于地質條件日趨復雜的天然氣探區，彈性參數與物性參數間的巖石物理關系往往具備極強的非線性，極易受到實際研究區巖性、孔隙結構、壓力、溫度等多種因素的影響，導致在大多數情況下難以建立起精確的巖石物理模型［14-17］。機器學習方法的出現為這類非線性建模問題提供了一種新的途徑。機器學習方法可以通過機器自主學習得到一種非線性映射關系，實現高度復雜的非線性函數逼近，具有強大的學習數據集本質和高度抽象化特征的能力。通常根據訓練是無監督的還是有監督的進行分類。無監督學習無須訓練數據集，直接基于輸入數據的分布或結構來對信息相似的數據進行分組和映射；監督學習則需要訓練數據集，包括輸入數據和標簽，標簽是輸入的響應值。監督學習的主要目標是從標記的訓練數據中學習出一個最優的映射模型，將已知領域知識與數據本身進行結合，能夠有效減少預測的多解性。在眾多的監督機器學習算法中，隨機森林（Random Forests，簡稱RF）近年來在地球物理學領域取得了較好的應用效果［18］。Breiman［19］提出的RF 是一種集合學習算法，結合了bagging 集合和隨機特征選擇的思想，預測結果由多個決策樹分類器投票決定。多個決策樹的作用相當于組合很多非線性關系形成更復雜的非線性關系，具有預測精度高、對異常值和噪聲數據容忍度高等優點，已廣泛應用于金融、生物、遺傳、圖像識別、醫學等領域。在地球物理領域，Harris 等［20］將隨機森林算法應用于地球物理和地球化學數據聯合巖性分類。宋建國等［21］針對儲層預測的復雜非線性及穩定性問題，將隨機森林回歸算法引入到地震儲層預測中，建立地震屬性與自然伽馬之間的非線性關系。王光宇等［22］考慮了不平衡樣本對隨機森林巖性分類問題的影響。Kuhn 等［23］利用地球物理和遙感數據對金礦附近未開采區域的巖性進行了分類研究。Cracknell 等［24］將RF 與SVM、樸素貝葉斯、K 近鄰和人工神經網絡進行了巖性預測效果比較，認為RF 優于其他機器學習算法，并且證明了RF 能夠以更簡單的輸入參數和更少的計算成本產生準確的結果。

以往研究結果表明，對于巖性和流體識別等離散數據的分類問題，利用若干個對目標敏感的地震衍生屬性，如振幅、頻率以及彈性參數等作為輸入特征變量，即可獲得較好的分類結果［25-27］，而對于含氣飽和度這類連續數值的回歸問題，特征變量的數量對預測結果的影響尚未明確。離散分類問題和連續值回歸問題在算法本質上差別不大，但對參與訓練的特征變量的數量依賴程度不同。連續值回歸問題可以看作是將連續值按極小的間隔離散化的分類問題，只是所分類別較多，對參與訓練的特征變量的數量要求也更大。通常情況下，訓練中涉及的特征變量越多，所攜帶的信息越豐富，訓練結果可能更準確、泛化性能更好［27］，但如果無限制地增加特征變量數量，會導致工作量巨大。另外，含氣飽和度訓練樣本的取值分布往往具有“非平衡”特征，尤其是復雜天然氣探區，含氣層往往薄薄地發育在大套背景巖性中，當高含氣層樣本過少，而低含氣層樣本過多時，會使訓練結果向低含氣層偏倚，導致含氣飽和度的預測準確率較低。

基于隨機森林（RF）預測含氣飽和度，引入合成少數類過采樣技術以消除樣本不平衡對RF 訓練的影響，采用自動特征變量擴展策略解決含氣飽和度回歸對特征變量數量的依賴，利用隨機森林對特征變量進行含氣飽和度預測重要性排名，優選重要性較高的特征變量進行最終隨機森林訓練，并將該方法在實際工區中進行應用，以期提高地震信息對天然氣藏含氣飽和度的定量預測能力。

1 方法原理

1.1 特征變量擴展

RF 算法用于含氣飽和度預測的一個關鍵步驟是要準備足夠的特征變量作為訓練集。Alvarez等［28］對縱波阻抗、橫波阻抗、縱橫波速度比、拉梅參數×密度、剪切模量×密度、拉梅參數/剪切模量、（拉梅參數-剪切模量）×密度、泊松比、楊氏模量×密度、體積模量×密度、泊松阻抗等11 種常用的地震彈性參數進行數學變換，得到了大量的地震衍生屬性作為孔隙度、含水飽和度與泥質含量等物性參數線性回歸的基礎屬性集，在常規碎屑巖物性參數預測中取得較好的應用效果。然而，且不論該方法采用線性回歸的合理性，實際上常用的彈性參數的數量就遠遠超過11 種，該方法可能會遺漏對目標敏感的彈性參數。另外，每個彈性參數的獲取都需要基于疊前地震反演或利用不同的變換公式轉換得到，自動化程度較低，且變換過程中也存在誤差積累和放大的風險。尤其是對于各向異性比較明顯的致密砂巖或頁巖氣藏，疊前地震反演本身就存在極大的不確定性。為克服人工準備大量特征變量的問題，利用擴展彈性阻抗（EEI）自動生成一系列彈性屬性作為特征變量。Whitcombe 等［29］在Connolly彈性阻抗方程的基礎上提出了EEI方程的定義：

式中：χ為角度，（°），取值-90°～90°；vp，vs，vp0和vs0分別為縱波速度、橫波速度、目的層平均縱波速度和平均橫波速度，m/s；ρ和ρ0分別為密度和目的層平均密度，kg/m3；k=vs2/vp2。

由式（1）可知，EEI可以由vp，vs和ρ這3 個基本的彈性參數計算得出，通過調整χ的大小可以對EEI進行調整，當其與一些彈性參數近似成正比，可以用于巖性或流體識別［29］。此外，EEI還可以對常見的測井屬性（如電阻率、伽馬）進行較好的擬合［30］。通過疊前地震反演技術易獲得vp，vs和ρ這3個基本的彈性參數體，使用不同值的EEI作為特征變量替代常規彈性參數。

首先，針對從疊前地震反演獲得的彈性參數存在一定誤差這一問題，直接從疊前地震反演得到的彈性參數數據體中提取井旁道的縱波速度、橫波速度和密度偽井曲線作為與含氣飽和度測井解釋標簽對應的彈性參數樣本，采用機器學習算法進行處理。即使訓練樣本帶有一定的誤差，機器學習也能在無意識下學習得到包含噪聲的映射模型，直接將帶有誤差的特征變量映射為含氣飽和度。需要注意的是，特征變量的誤差也不能過大，會削弱有效信息。其次，設定角度χ 的變化步長，將縱波速度、橫波速度和密度偽井曲線帶入式（1），自動生成一系列不同角度的EEI曲線。然后，根據Alvarez等［28］的數學變換思想，采用對數、指數、倒數、平方、開方運算對擴展彈性阻抗進一步擴充，以設定χ為5°為例（表1），每個數字代表一個特征變量，可得到222 個彈性屬性作為特征變量數據集。最后，將生成的井旁道特征變量和對應的含氣飽和度測井解釋標簽作為監督學習的原始訓練集。

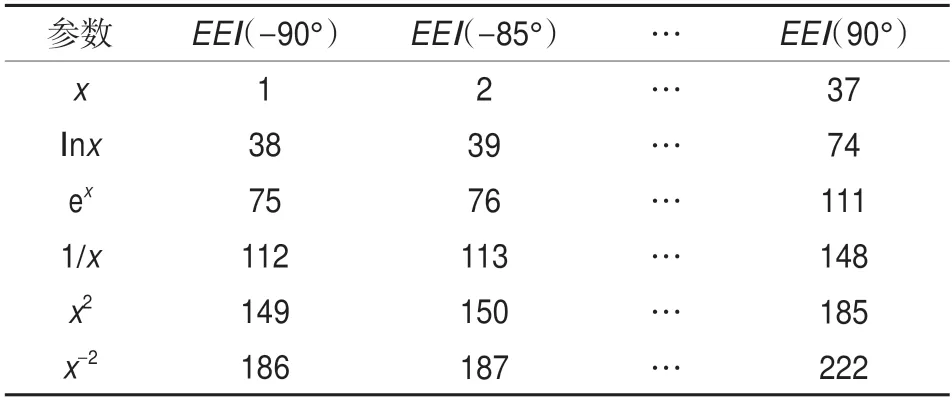
表1 擴展特征變量Table 1 Extended feature variables

在實際操作中，還可以針對具體條件來設定需要擴展的特征變量的數量。為了盡量不遺漏潛在的目標敏感彈性屬性，χ 的變化步長可以設定得更小，以獲得更多的特征變量。另外，也可以使用或增加其他的數學運算方法來進行自動轉換，進一步擴充特征變量的種類來增加特征變量數據集中有敏感性屬性的可能性。

1.2 樣本平衡化處理

RF 算法的核心是采用Bootstrap 抽樣法對原始樣本集進行重新抽樣，隨機生成k個子訓練集S1，S2，...，Sk。通過Bootstrap 抽樣，每個訓練子集平均包含約63.2%的樣本，而剩余37.8%的“袋外”樣本則用于驗證［19］。每個子訓練集所包含的元素不盡相同，這可以保證決策樹的多樣性，使得訓練模型具備泛化性，但在Bootstrap 抽樣過程中，所有樣本每次抽樣的概率都是相同的，這就意味著在不同類別樣本數量差別很大的樣本集上訓練時，往往會出現分類面向多數類樣本偏倚的現象，少數類樣本無法獲得理想的分類效果。近幾年來，機器學習中不平衡數據的分類問題受到了越來越多的關注［31］，這里的“不平衡數據”是指分類問題中對應于每個類別的樣本數量是不同的，而且數量差異較大。這種不平衡數據往往會惡化機器學習算法的性能［32］，如在進行巖性識別時，當樣本集中目標巖性（如含氣砂巖）的樣本數量過少，而非目標巖性（如泥巖）的樣本數量過多時，會使預測結果向非目標巖性偏倚，導致目標巖性的預測準確率較低。同樣，對于含氣飽和度回歸也有這樣的問題。在中國西部地區，有利氣藏通常厚度較小，發育在大套地層中，若含氣飽和度較高的有利儲層訓練樣本數較少，而含氣飽和度較低的非有利儲層的訓練樣本數較多，RF回歸器的訓練可能會偏向于非有利儲層，影響有利儲層的含氣飽和度回歸精度。

對于不平衡數據的處理一般有過采樣和欠采樣2 種方法。過采樣是通過復制少數類樣本來增加其規模，欠采樣則是隨機刪除一些多數類樣本的數量。考慮到機器學習含氣飽和度回歸主要以測井數據作為訓練樣本，而測井成本較高，往往數量也不多，因此不刪除多數類樣本，而是采用過采樣方法來處理少數類樣本。在機器學習領域，應用較多的過采樣方法是合成少數類過采樣技術（Synthetic Minority Oversampling Technique，SMOTE），該技術通過分析少數類樣本的特征，人工合成新的樣本，并將新的樣本加入到數據集中，直到各類樣本的數量趨于平衡，形成一個大的平衡訓練集，其實施步驟如下［33］：

（1）對于少數類中的每個樣本，利用歐式距離計算其與少數類中所有樣本的距離，并獲得m個最近的鄰點。

（2）根據不平衡類比例設定抽樣比例，確定少數類樣本的抽樣放大最終數量為N。對于少數類中的樣本x，從m個最近的鄰點中隨機選擇幾個樣本y，構建新的樣本z：

式中：rand（0，1）為隨機數，取值0～1。

（3）重復步驟（1）—（2），直到少數類樣本數量增加到預先設定的數值N。

然而，該方法并沒有考慮樣本的邊界問題，可能會造成樣本取值的大量重疊，在離群點附近也會產生一些不能提供有效信息的樣本，降低學習性能。邊界合成少數過采樣技術（BSMOTE）是在SMOTE 基礎上改進的過采樣算法［34］，如圖1 所示，該算法在采樣過程中將少數類樣本分為“安全”“危險”和“噪聲”3 類，“安全”類別是指鄰域超過一半的樣本是少數類樣本（如圖1 中點A 所示）；“危險”類別是指鄰域超過一半的樣本為多數類樣本，視為邊界上的樣本（如圖1 中點B 所示）；“噪聲”類別是指樣本被多數類樣本包圍（如圖1 中的點C 所示），只對被標記為“危險”的樣本進行過采樣合成新樣本，可以改善樣本的類別分布。

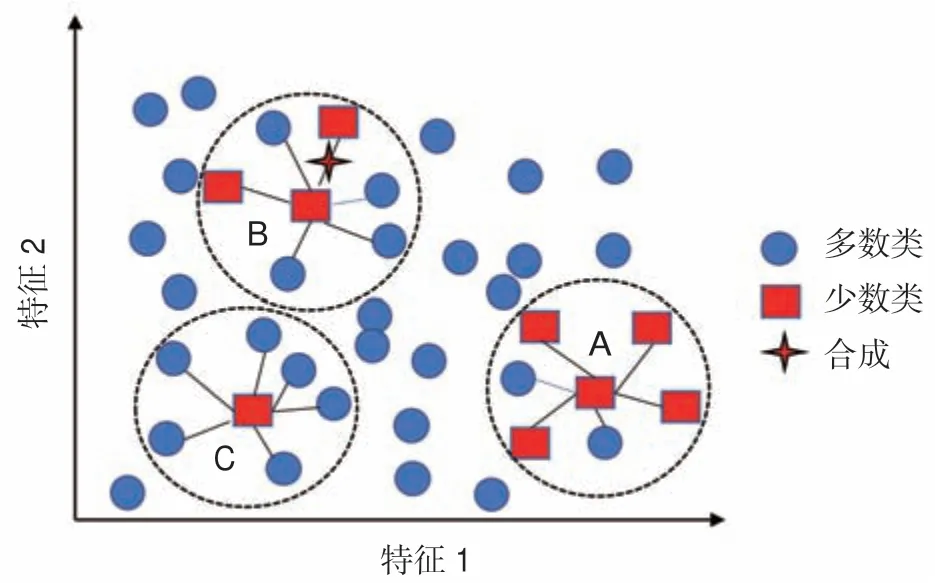
圖1 BSMOTE 原理示意圖Fig.1 Schematic diagram of BSMOTE

1.3 隨機森林回歸器構建

作為一種數據驅動算法，RF 對每個Bootstrap抽樣得到的子訓練集S1，S2，...，Sk分別進行決策樹建模，從而顯著提高了模型的準確性和魯棒性，在處理各種復雜的預測和分類問題時表現出了出色的性能。在RF 中，每棵決策樹都獨立地為給定的數據樣本提供一個預測值，然后將全部k棵決策樹的預測值取平均作為最終的輸出值。這種集成方法在處理高維數據和大規模數據時，可以有效地應對過擬合和欠擬合的問題。決策樹構建算法采用Breiman 提出的CART 算法［23］，其基本步驟為

（1）特征選擇。CART 算法對于每一個節點都需要選擇最佳的特征進行分裂，通常基于基尼系數來進行特征選擇，以實現節點的最佳分裂。

（2）節點分裂。根據選定的特征，對節點進行分裂，使得各個子節點中的樣本盡可能屬于同一類別（分類樹）或者具有相似的回歸值（回歸樹）。

（3）遞歸構建。重復對子節點進行上述分裂操作，直到滿足停止條件。如在分類樹中，可以設定樹的最大深度或者節點中樣本數量的最小閾值；在回歸樹中，也可以設置類似的停止條件。

（4）剪枝。構建完整的決策樹后，可以對樹進行剪枝，通過降低樹的復雜度來提高模型的泛化能力，防止過擬合。

根據本文提出的特征變量擴展方法，可以將疊前地震反演得到的縱波速度、橫波速度和密度數據體生成222 個特征變量作為RF 回歸器的輸入數據。然而，擴展彈性阻抗變量之間本身也具有一定的相關性，大量信息重復的特征變量可能帶來過多的冗余信息和計算消耗。有些特征變量可能是極為敏感的指標參數，而有的特征變量可能包含的有效信息很少，選擇對目標回歸貢獻較大的特征變量可以加快過程并提高預測的準確性。

RF 的另一個優點是可以提供變量重要性（Variable important，VI）的衡量標準，根據特征變量的預測能力進行排序［35］。用隨機森林進行特征重要性評估的思想就是衡量每個特征在隨機森林中的每棵樹上所做的貢獻，取所有樹的平均貢獻來比較特征變量的貢獻大小。在RF 中，有Gini 重要性和互換精度重要性2 種得分評價標準，對于含氣飽和度預測這類回歸問題宜采用互換精度重要性來計算VI 得分。根據Bootstrap 采樣思想，每棵決策樹都有子樣本集37.8%的“袋外”樣本在構建過程中并沒有使用，可以被用來計算特征變量的重要性。

第i棵樹，第j個特征變量Xj的VI 得分［35］為

取所有樹的平均VI 得分作為變量的最終VI得分，根據VI 得分的排名，選擇排名靠前的特征變量作為RF 回歸器構建的最終使用特征變量。

2 實施流程

基于特征變量擴展的含氣飽和度隨機森林預測方法在實際生產中的實施流程如圖2 所示，主要有4 個步驟：

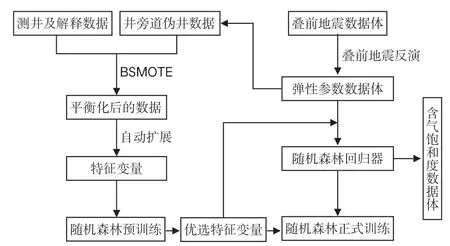
圖2 隨機森林含氣飽和度預測流程Fig.2 Workflow of gas saturationprediction by random forests

（1）訓練樣本平衡化處理。抽取井旁道縱波速度、橫波速度和密度3 個彈性參數的疊前地震反演結果作為基本特征變量樣本，根據測井有利儲層分類解釋結果，采用BSMOTE 方法對基本特征變量和對應的含氣飽和度樣本進行平衡化處理。

（2）特征變量樣本擴展。對平衡化后的彈性參數樣本應用表1 所列擴展方式進行自動擴展并編號，得到擴展的特征變量樣本。

（3）隨機森林回歸器訓練。分為預訓練和正式訓練，先開展RF 預訓練，根據式（3）對各特征變量進行重要性排名，優選排名靠前的特征變量，輸入優選的特征變量樣本和目標物性參數標簽，進行RF 正式訓練，得到最優的回歸器。

（4）含氣飽和度預測。根據步驟（3）中優選的特征變量的編號，依據表1 中對應的擴展方式，將彈性參數疊前地震反演成果數據體整體轉換為特征變量數據體，輸入到訓練好的隨機森林回歸器中，輸出預測的含氣飽和度數據體。

3 應用實例

以中國西部某天然氣藏研究區為例驗證新方法的有效性。該研究區氣藏埋藏較深、分布廣泛、有效儲層厚度大。早期部署的探井獲得高產工業氣流，顯示出該區域氣藏巨大的資源潛力，但隨著探井部署的增多，發現產能橫向差異較大，鉆井風險大，需要精細刻畫有利氣藏的分布。然而，該區域氣藏經過多期礦物轉化，巖石礦物的組成和孔隙結構相比淺層氣藏更加復雜，彈性參數不僅與含氣飽和度有關，還受巖相、孔隙度和孔隙結構的影響，巖石物理模型難以準確建立，導致常規基于巖石物理模型的含氣飽和度反演方法的精度較低，難以有效指導勘探井位的部署。因此，有必要嘗試基于數據驅動的方式獲取高精度含氣飽和度信息來減少勘探風險。

3.1 單井分析

圖3 為研究區某重點井的含氣飽和度測井解釋曲線及從縱波速度、橫波速度和密度疊前地震反演數據體中提取的對應井旁道偽井曲線。可以看到含氣飽和度解釋曲線與縱波速度、橫波速度和密度偽井曲線間并沒有直觀的線性關系，利用簡單的數學公式難以將彈性參數進一步轉換為含氣飽和度。

圖3 中國西部某天然氣藏含氣飽和度測井解釋曲線及井旁道彈性參數反演曲線Fig.3 Log interpretation curve of gas saturation and inversion curves of elastic parameters from the uphole trace in a natural gas reservoir in western China

圖4 為不同角度的EEI曲線和利用圖3 中縱波速度、橫波速度和密度曲線計算得到的拉梅阻抗（拉梅參數×密度）λρ曲線。λρ通常被用作反映巖石剛度變化的巖性和流體識別指標［36］。可以觀察到，不同角度的EEI曲線具有不同的變化形態，突出的特征也不同，當角度為20°時，EEI（20°）與λρ曲線非常相似，相關系數達到0.97，表明EEI隨著角度的變化確實可以逼近一些常見的彈性參數。因此，本文提出的利用EEI隨角度變化的這種特性開展特征變量的擴展具有一定現實依據。

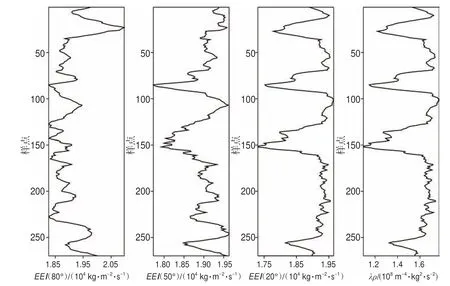
圖4 中國西部某天然氣藏3 個不同角度的EEI 曲線與拉梅阻抗曲線Fig.4 Well curves of EEI withthree different angles andLame impedance curve in a natural gas reservoir in western China

根據表1 的生成方式，得到222 個擴展變量進行VI 排序。如圖5 所示，并非每個變量對含氣飽和度預測都很重要，許多變量的重要性非常低，這表明存在信息冗余。最高、最低VI 變量分別為EEI（20°）-2和EEI（50°）2，將這2 個變量對應的特征變量曲線與測井解釋的含氣飽和度曲線進行對比（圖6）可知，最高VI 特征變量曲線大致上可以反映含氣飽和度曲線的變化，而最低VI 特征變量曲線與含氣飽和度曲線差異大，證明了VI 的可靠性。

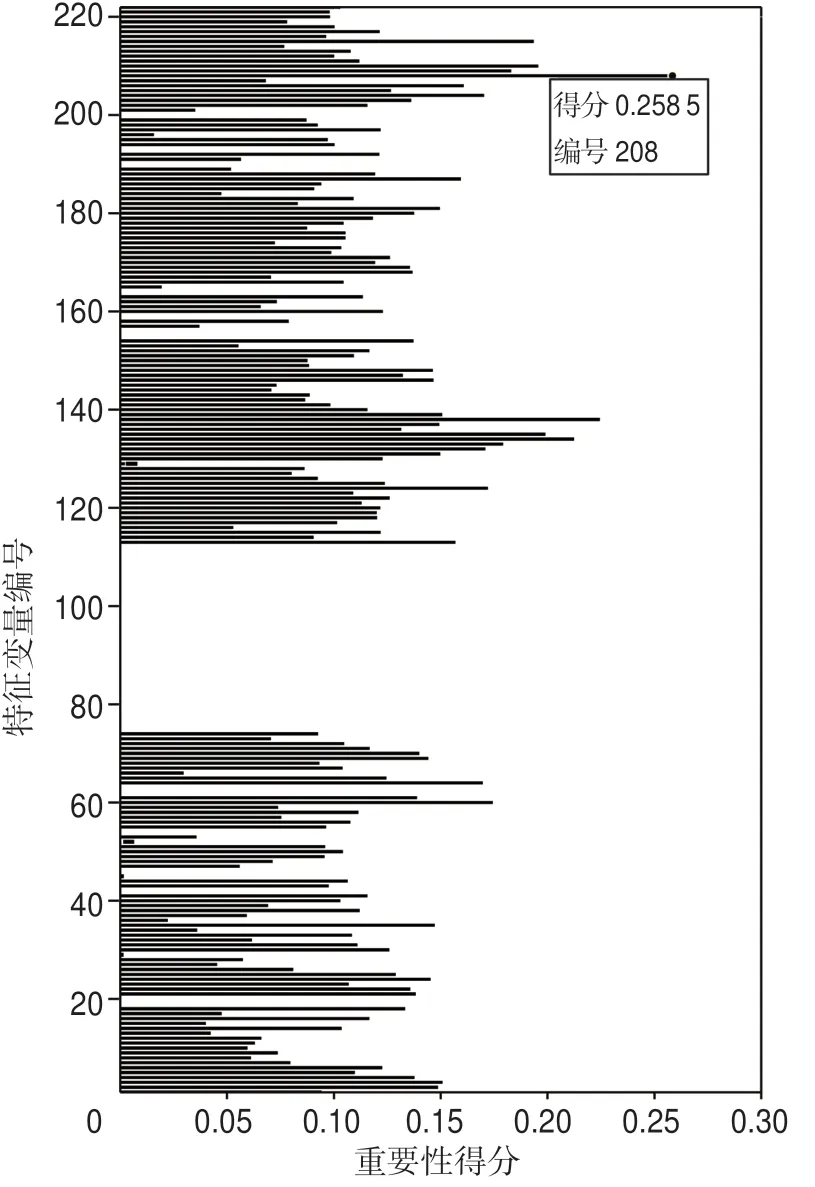
圖5 中國西部某天然氣藏含氣飽和度隨機森林預測時222 個擴展特征變量的重要性得分情況Fig.5 Importance scores of 222 extended feature variables in random forests prediction of gas saturation in a natural gas reservoir in western China

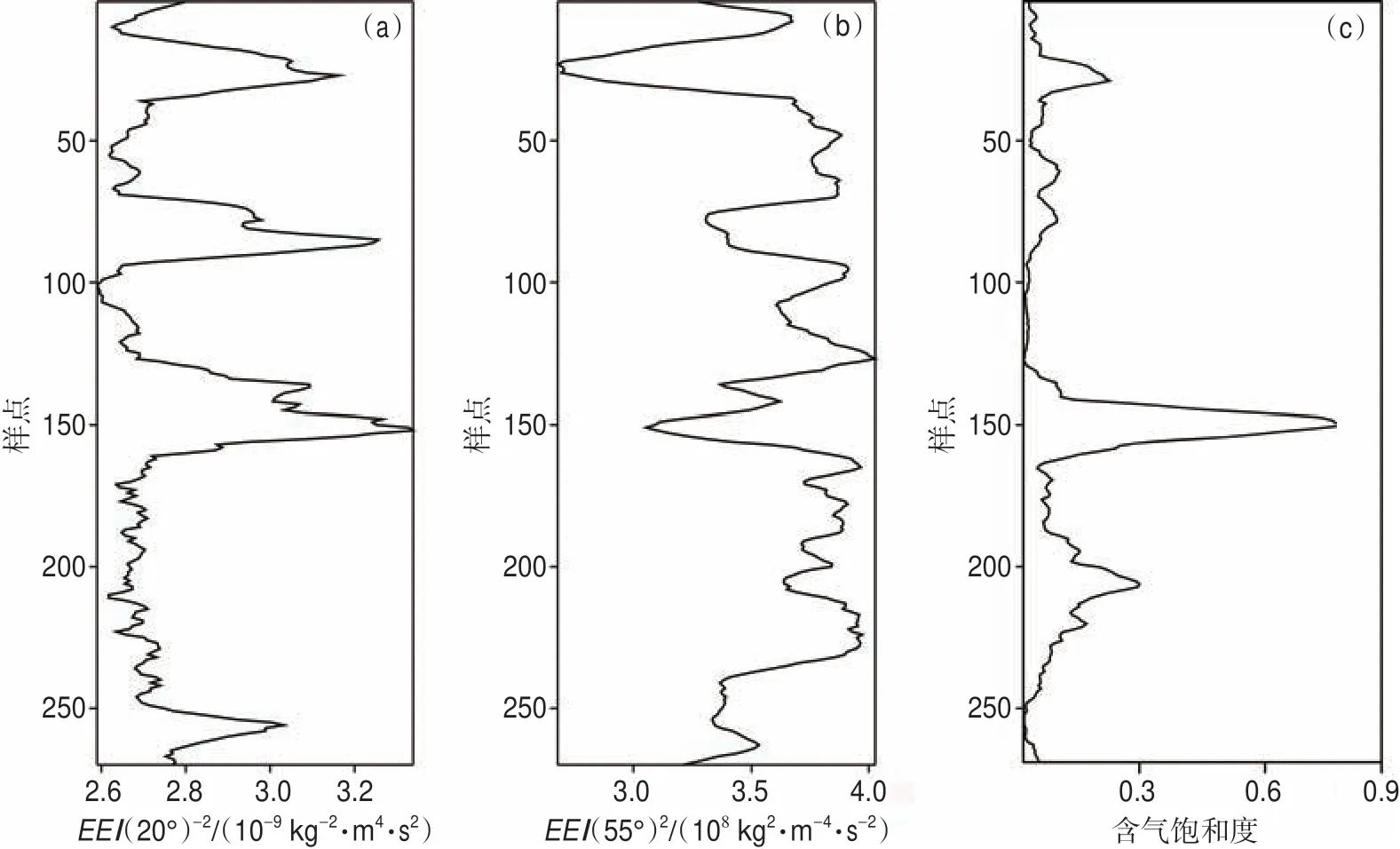
圖6 中國西部某天然氣藏含氣飽和度隨機森林預測時最高（a）、最低（b）重要性特征變量曲線與含氣飽和度（c）形態對比Fig.6 Curve shape comparison of the highest（a）and lowest（b）importancefeature variable curves predicted by random forestsand logging interpretation curves gas saturation（c）in a natural gas reservoir in western China

綜上所述，與λρ相關性最高的特征變量曲線（參見圖4）、重要性最高的特征變量曲線（圖6）的整體形態均與密度曲線相似（整體方向上有所不同），這也說明了利用擴展特征屬性能夠代替常規需要人工一一提取或轉換計算的彈性參數。本文中提取的擴展策略能夠得到222 種擴展屬性供優選作為含氣性敏感的特征變量，但并不能只用一個擴展特征變量就預測含氣飽和度，即使是重要性最高的特征變量曲線與含氣飽和度曲線在細節上仍有一定的差異，還需要其他特征變量來參與修正。

按照變量重要性從高到低的排序，依次加入到RF 訓練中，如圖7 所示，僅以重要性最高的特征變量進行單個訓練，預測的含氣飽和度曲線與真實含氣飽和度曲線的相關系數為0.47，隨著特征變量數量的增加，相關系數先上升，當數量達到約20 個時（如圖7 中紅點所示），相關系數趨于平緩，約為0.90。因此，可以認為在本例中只需前20 個特征變量即可滿足訓練要求。

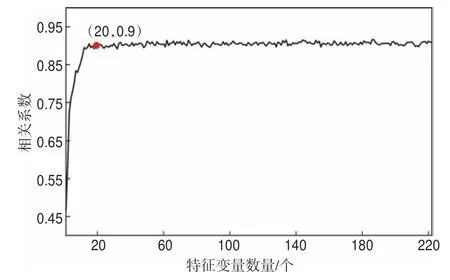
圖7 中國西部某天然氣藏基于特征變量擴展的含氣飽和度隨機森林預測結果和含氣飽和度測井解釋的相關系數-特征變量數量曲線Fig.7 Variations in the corresponding correlation coefficient between the gas saturation predicted by random forestsand the the real gas saturation curve in relation to the number of variables in a natural gas reservoir in western China

將未平衡化的全部222 個變量、VI 前20 個變量和11 個常用彈性參數分別作為隨機森林回歸器訓練的特征變量，預測得到的含氣飽和度曲線如圖8 所示。全部222 個變量的預測曲線與VI 前20個特征變量的預測曲線幾乎重合，且與真實含氣飽和度曲線的吻合程度較高，明顯優于利用11 個常用彈性參數參與訓練的預測結果，但在高含氣飽和度區間（如圖8 中黑色箭頭所示）有明顯的偏差。分析認為處于高含氣飽和度區間段的樣本占比較小，導致RF 回歸器的訓練偏向低含氣飽和度樣本。因此，需要對參與訓練的樣本進行平衡化處理。

圖8 中國西部某天然氣藏3 種不同的特征變量的含氣飽和度隨機森林預測結果與含氣飽和度測井解釋曲線對比Fig.8 Comparison among the gas saturation curvespredicted by random forestswith three different feature variables and the real gas saturationcurve in a natural gas reservoir in western China

利用BSMOTE 方法對預測的含氣飽和度曲線及其對應的特征變量進行平衡化處理后，原始樣本中低含氣飽和度的樣本數量未發生改變，而高含氣飽和度的樣本數量明顯增加，且取值更加豐富，高、低含氣飽和度樣本數量大致達到平衡（圖9）。

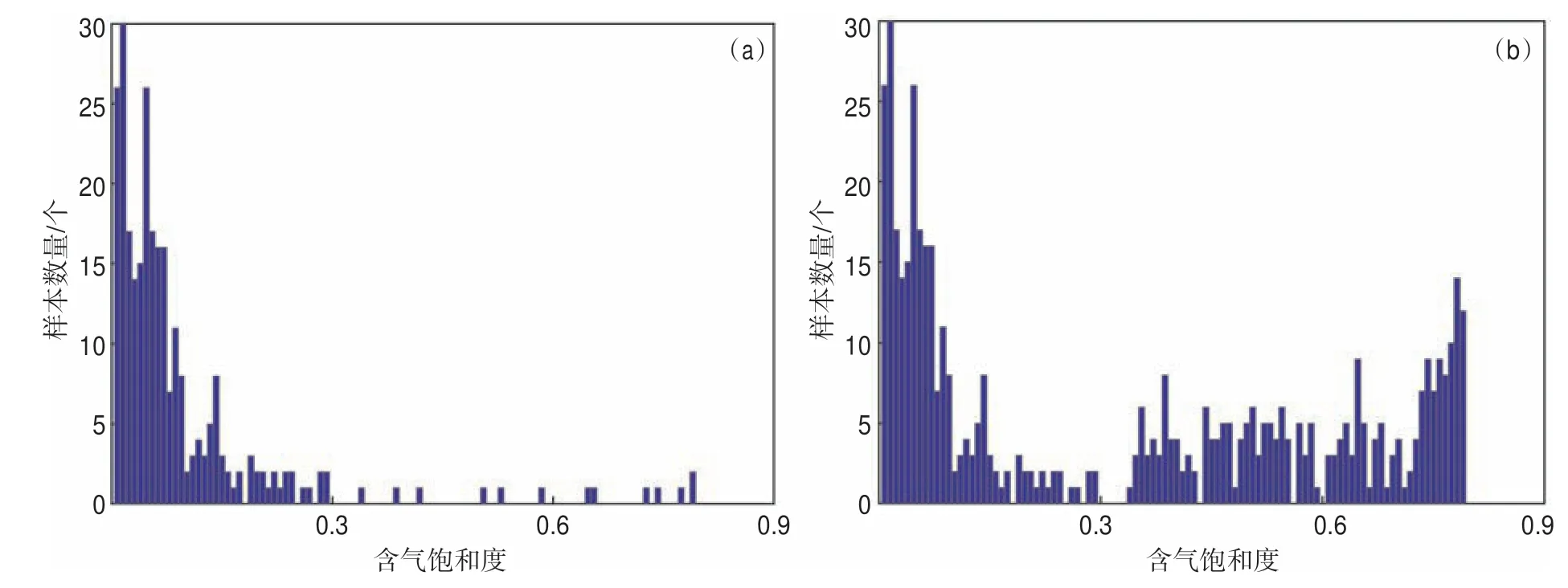
圖9 中國西部某天然氣藏含氣飽和度樣本平衡化前（a）、后（b）直方統計Fig.9 Histogram ofgas saturation before（a）and after sample balancing（b）in a natural gas reservoir in western China

對經過BSMOTE 處理后的樣本進行訓練，采用VI 排名前20 的特征變量參與訓練，高含氣飽和度區間的預測結果有明顯的改善（圖10），相關系數由平衡前的0.903 2 上升到平衡后的0.985 5。這也說明了對于含氣飽和度這類不平衡數據的預測，樣本平衡問題是不可忽視的。

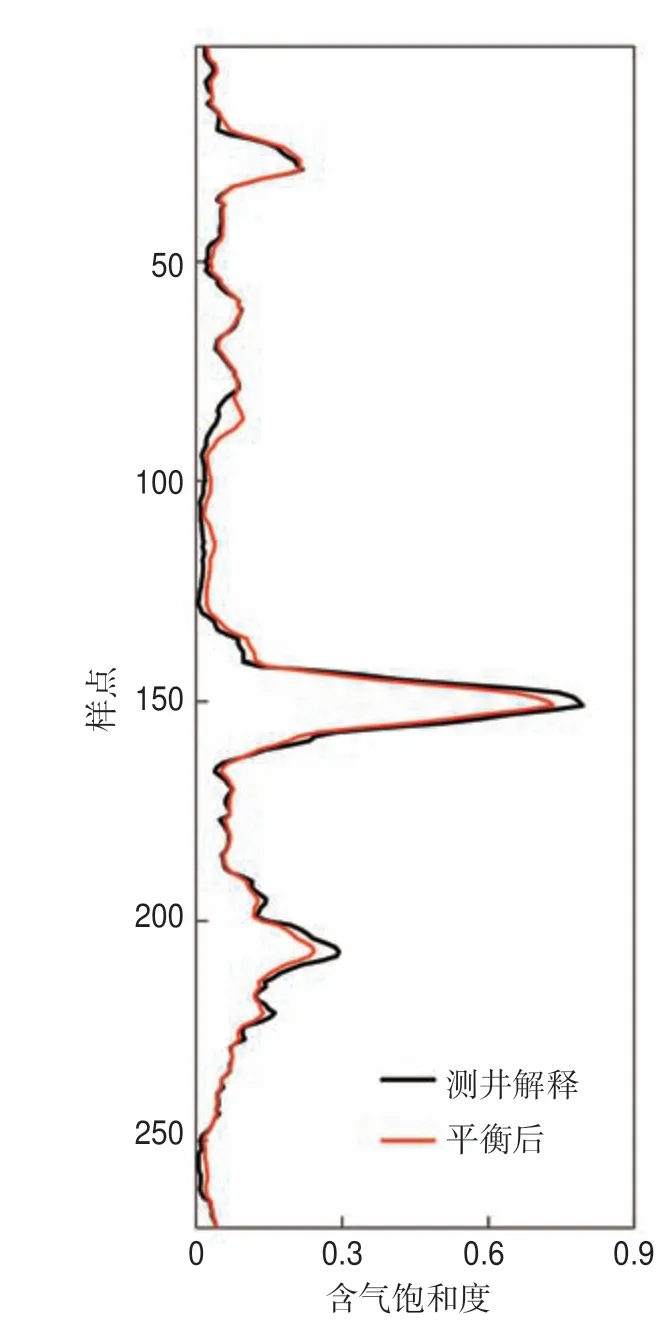
圖10 中國西部某天然氣藏樣本平衡化后含氣飽和度隨機森林預測結果與含氣飽和度測井解釋曲線對比Fig.10 Comparison between the gassaturation curves predicted by random forestsafter sample balancing and the real gas saturation curve in a natural gas reservoir in western China

3.2 二維資料應用分析

研究區前期勘探經驗和綜合分析表明，含氣飽和度與其他物性參數具有較好的線性關系，找到高含氣飽和度區域通常就意味著能找到有利氣藏。因而，生產上需要利用地震儲層預測方法優選含氣飽和度較高的目標區域為鉆井的軌跡設計提供依據。

研究區含氣飽和度測井解釋結果（圖11 中黑色曲線）顯示目的層上部發育1 套含氣飽和度較低的差氣層（圖11 中藍色箭頭所示），下部發育1 套含氣飽和度較高的高產氣層（圖11 中紅色箭頭所示）。將區內A 井和C 井作為訓練參與井，B 井作為驗證井，分別采用本文方法和常規方法（基于常規未平衡化的11 個彈性參數作為RF 的輸入）預測含氣飽和度并繪制連井剖面（圖11）。結果顯示，采用常規方法解釋該區發育上、下2 套含氣飽和度較高且值相近的儲層（圖11a 中虛線框所示），很容易被解釋為具備同一品質的儲層，而本文方法解釋的這2 套儲層含氣飽和度差異較大，下部的儲層（圖11b 中虛線框所示）含氣飽和度明顯更高，這一結果與測井解釋結果一致。

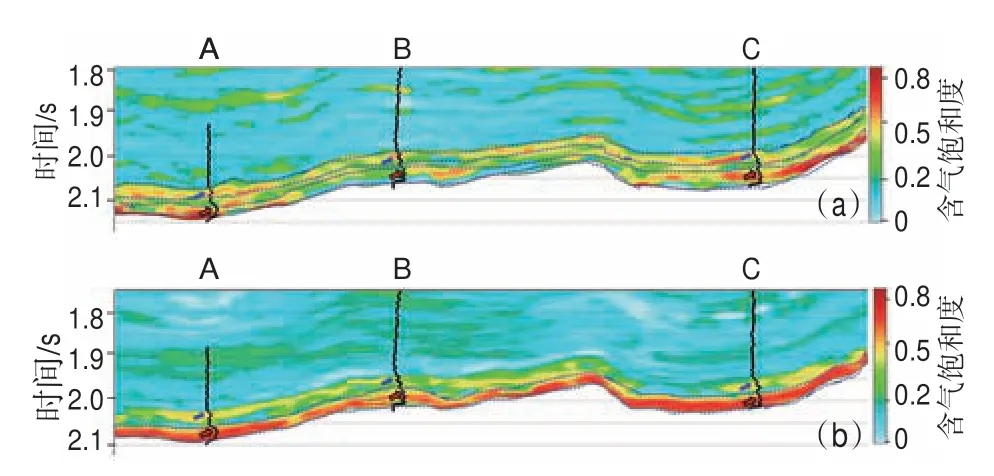
圖11 常規方法（a）與基于特征變量擴展的隨機森林法（b）預測的含氣飽和度剖面Fig.11 Gas saturation profiles predicted by conventional method（a）and random forestswith feature variable extension（b）

為了進一步驗證本文方法的正確性，抽取驗證井B 井的井旁道反演結果（圖12）可知，本文方法預測結果整體上與含氣飽和度測井解釋曲線吻合較好，而常規方法在高含氣飽和度部位出現了較大的偏差，很可能會被錯誤地解釋為差氣層。

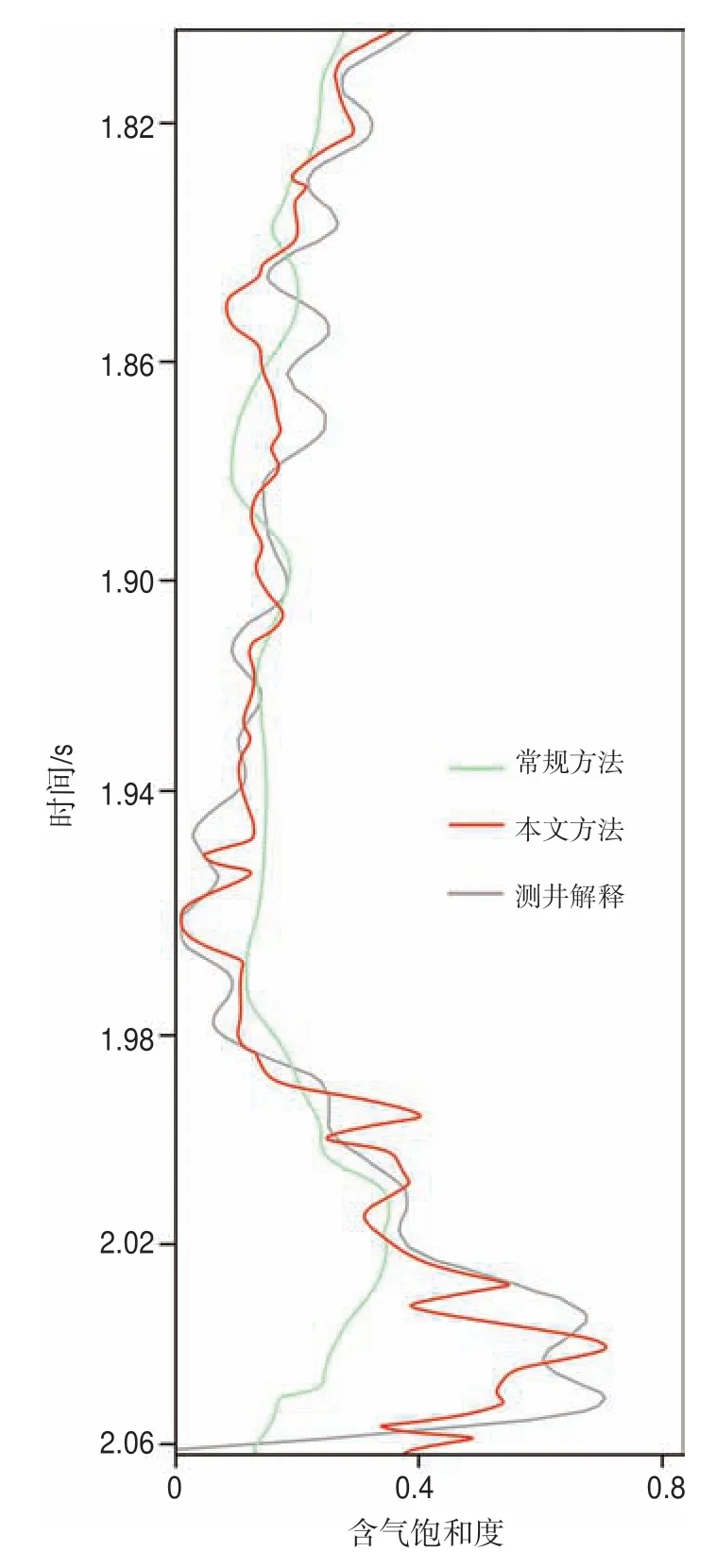
圖12 采用常規方法和基于特征變量擴展的隨機森林法預測的驗證井含氣飽和度對比Fig.12 Comparison of gas saturation of validation well predicted by conventional methods and random forestswith with feature variable extension

4 結論

（1）對于含氣飽和度這類連續型數值回歸問題，基于數據驅動的機器學習方法為取得最佳性能，需要大量的特征變量作為訓練集，利用擴展彈性阻抗自動生成222 個擴展彈性屬性作為機器學習的訓練集，能夠大幅減少特征變量提取和優選的人工工作量。

（2）大量信息重復的特征變量會帶來過多的冗余信息和計算消耗，利用隨機森林預訓練對特征變量進行重要性排名，優選對含氣飽和度預測重要性較高的特征變量參與正式訓練，能夠有效減少信息的冗余。

（3）“不平衡數據”特征會惡化機器學習算法的性能，而復雜氣藏的含氣飽和度的取值分布往往也具有“不平衡”特征，引入邊界合成少數類過采樣技術能有效解決儲層和非儲層的含氣飽和度樣本取值分布不平衡導致的隨機森林回歸器訓練偏倚的問題。

（4）基于特征變量擴展的含氣飽和度隨機森林預測方法在實際資料應用中能有效增強隨機森林算法在含氣飽和度地震預測方面的能力，且特征變量擴展策略對于孔隙度、有機質含量等其他氣藏物性參數的機器學習預測同樣有借鑒意義。