考慮光壓力和熱載荷的太陽帆薄膜力學行為分析

陳金鐸，史愛明，樊世超

（1.西北工業大學航空學院，西安 710072；2.北京衛星環境工程研究所，北京 100094）

0 引言

太陽帆利用帆面反射太陽光獲取光壓力，實現光壓加速。為提高帆面光壓-引力比，太陽帆薄膜厚度低至10 μm 量級，導致薄膜穩定性降低。Dowell 構建了太陽帆膜在光壓力作用下的運動方程，通過類比壁板氣動彈性控制方程，指出光壓力誘導薄膜顫振［1］。

根據Dowell［1］與Macneal［2］推導，作用于薄膜的光壓力分為切向光壓力和法向光壓力，前者與薄膜形變呈線性關系，后者獨立于薄膜形變。Dowell 在其論文中指出，對于線性結構模型，法向光壓力不影響薄膜顫振邊界，但未考慮法向光壓力對薄膜力學行為影響。Chen 等［3］沿用線性結構模型描述薄膜形變，通過光壓力的電磁波模型，指出光壓力與薄膜厚度耦合，因此薄膜的光壓彈性問題與壁板氣動彈性問題存在差異。相關太陽帆薄膜力學行為研究也通常基于線性結構模型描述薄膜形變［4-5］。在Chen 等［3］論文中指出，法向光壓力導致薄膜形成大幅值靜變形。線性結構模型不能考慮薄膜大變形導致的幾何非線性。利用von Kármán 大變形理論描述壁板形變時，作用于壁板的靜壓差顯著增大壁板顫振的臨界動壓［3，6-7］。類比氣動彈性壁板非線性動力學方程，作用于薄膜的法向光壓力在數學形式上等價于施加在壁板的靜壓差。因此，使用von Kármán大變形理論描述薄膜形變時，法向光壓力是影響薄膜力學行為的關鍵物理量。

光輻射熱是航天器普遍面臨的問題。受日蝕影響，近地軌道航天器所受太陽輻射呈現周期性變化［8-13］，航天器由陰影區進入光照區時，作用于航天器的光輻射熱載荷會激發太陽翼［12］、太陽帆支桿［10］等結構動力學響應。此外，深空探測太陽帆需接近太陽獲取更大光壓力［14］，在此過程中，太陽帆所受太陽輻射逐漸增大形成光輻射熱載荷，導致薄膜穩定性降低［15-18］，并影響薄膜非線性振動特性。

本文基于von Kármán 大變形理論描述薄膜結構，耦合光壓力與熱載荷，考察太陽帆薄膜的力學行為特性。

1 模型構建

1.1 光壓模型

考慮圖1 所示薄膜模型，x，z分別表示沿薄膜長度方向和厚度方向的坐標，薄膜長為a，厚度為h。薄膜兩端夾緊于兩側支桿［3，4，19］。薄膜橫向位移記為w，作用于薄膜的光壓力包含與薄膜形變相關的切向光壓力

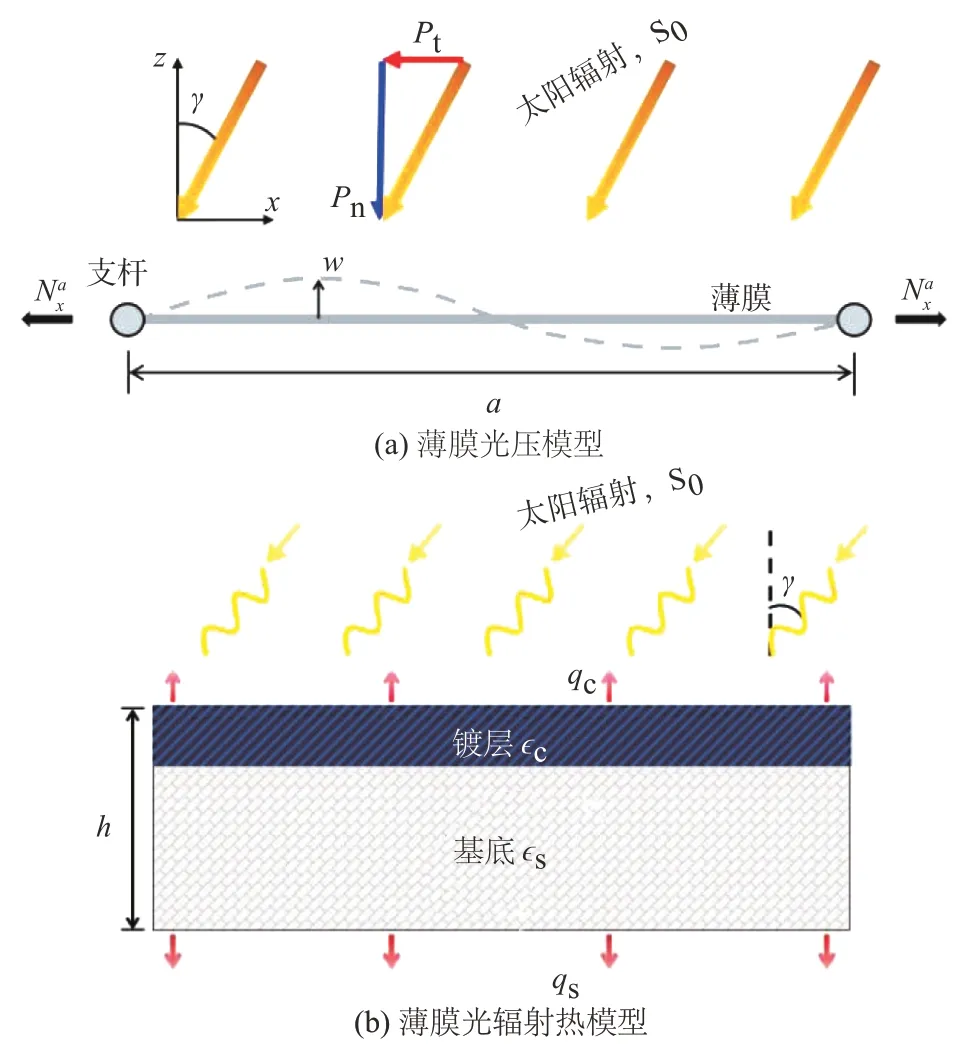
圖1 薄膜光壓載荷和熱載荷模型Fig.1 Solar pressure load and thermal load model applied on membrane

以及與薄膜形變無關的法向光壓力

式中：S0表示入射太陽輻射通量；R表示薄膜反射率；γ表示太陽輻射入射角；c表示光速。作用于薄膜總光壓力為切向光壓力與法向光壓力的矢量和，其中太陽帆依靠法向光壓力實現光壓推進。

1.2 光熱模型

除反射太陽輻射外，太陽帆薄膜會吸收部分太陽輻射，進而加熱薄膜形成熱載荷。薄膜在吸收太陽輻射同時向外進行熱輻射，如圖1（b）所示。薄膜溫度可基于熱量平衡條件導出。薄膜對太陽輻射吸收率記為A，可得薄膜吸收輻射通量為qin=S0Acosγ。薄膜向外熱輻射滿足Stefan-Boltzmann 定律q=?σT4，其中?為熱輻射系數，σ和T分別為Stefan-Boltzmann 常數和薄膜溫度，且有σ=5.67×10-8W·m-2·K-4。太陽帆薄膜通常在薄膜基底上增加金屬鍍層以增大薄膜反射率［20］，如圖1（b）所示，因此設薄膜鍍層與基底具有不同的熱輻射系數，計算中取?c=0.81，?s=0.86，下標c 和s 分別表示薄膜鍍層和基底。

設薄膜溫度沿薄膜表面均勻分布。由于太陽帆薄膜很小的薄膜厚度（10 μm 量級［1，3-4］），因此設薄膜溫度沿薄膜厚度同樣均勻分布。根據熱量平衡條件，吸收的太陽輻射通量等于薄膜向外輻射通量［21］，即

由式（3）可得在熱量平衡條件下，薄膜溫度為

由上式可知，太陽輻射通量變化導致薄膜溫度改變。記薄膜溫度增量為ΔT，則由溫度變化引起的面內熱應力為

式中：E為薄膜彈性模量；α為薄膜熱膨脹系數；ν為泊松比。

1.3 運動方程

基于von Kármán壁板理論構建薄膜運動方程

將式（1），（2），（5），（7）代入式（6），并無量綱化可得

為滿足兩端固支邊界條件，設薄膜無量綱橫向位移

式中：m為模態數；Γ為模態振幅。

將式（10）代入式（8），利用Galerkin法可得

利用龍格-庫塔時間推進算法求解上式。

2 模態收斂性分析

薄膜運動方程式（8）與氣動彈性問題中壁板運動方程滿足相似數學形式，對常見氣動彈性問題，6階近似Galerkin 方法能夠得到較高精度結果［6］。針對本文太陽帆薄膜光壓彈性問題，根據式（9）中無量綱熱應力NˉxT和無量綱法向光壓力Pˉn可知，很小的薄膜厚度導致作用于薄膜的無量綱載荷量級很大，為分辨薄膜力學行為特性，需考察Galerkin 方法模態數對薄膜力學行為的影響。

在本文計算中，取E=9.67×109N/m2，α=5×10-6K-1，ν=0.33，cˉd=0.1，R=0.9，A=0.1，h=25 μm，a=10 m，S0=1 360 W/m2。圖2（a）給出薄膜靜變形幅值隨模態數變化關系。當模態數N=2 時，薄膜在相同條件下進行動力學振動而非靜變形，因此圖中最低模態為4 階。由圖2（a）可知，在分析薄膜靜變形時，4階模態計算結果即可分辨薄膜靜變形特征。

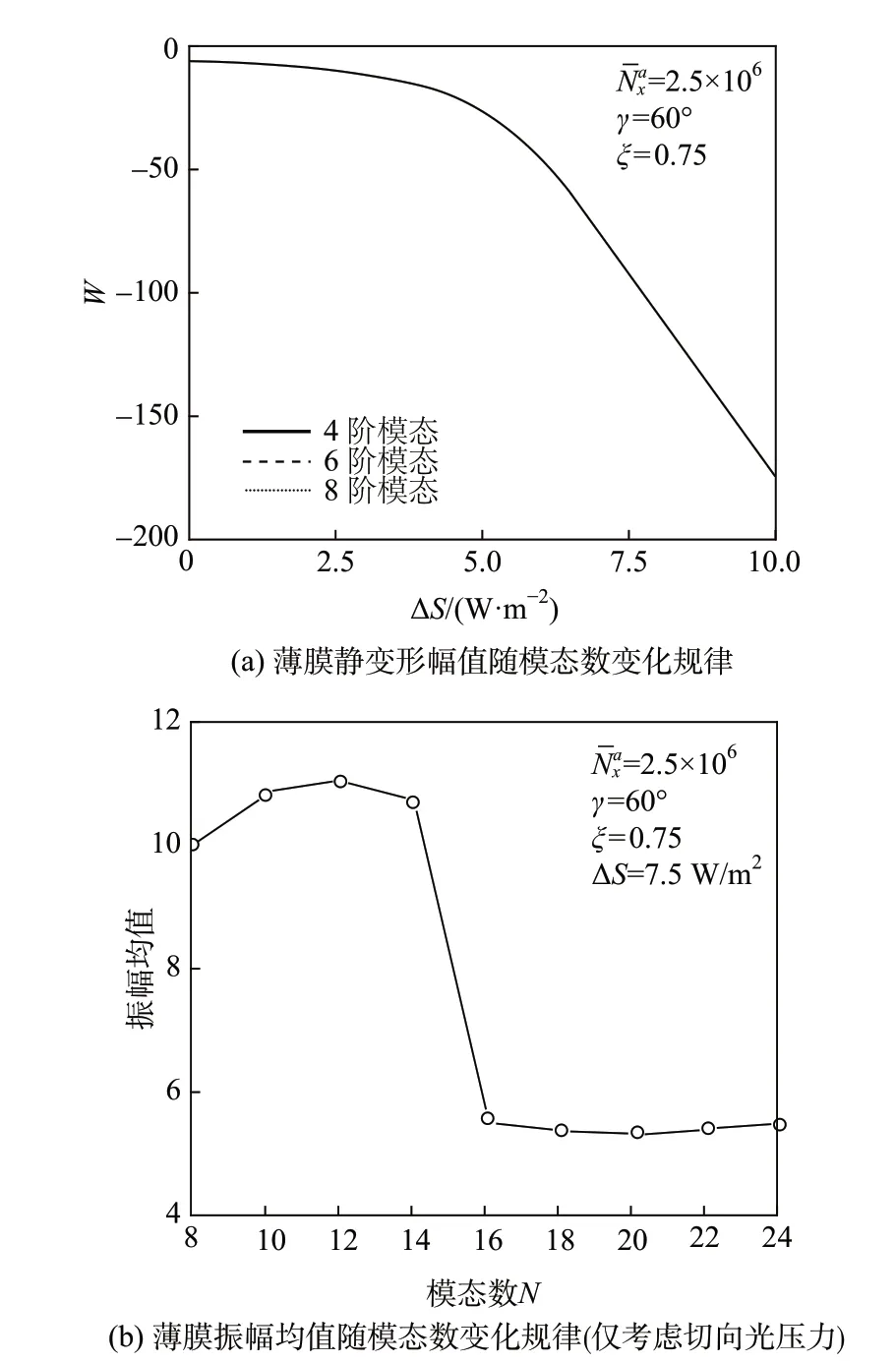
圖2 模態數對薄膜力學行為的影響Fig.2 Modal numbers effects on the membrane behaviors

為考察模態數對薄膜振動特性影響，圖2（b）給出當光輻射通量差ΔS=7.5 W/m2時，薄膜在無量綱時間［99.99，100］區間內振幅均值隨模態數的變化規律。如下文所述，法向光壓力抑制薄膜振動，因此計算圖2（b）中薄膜振動特性時，略去法向光壓力。在本文分析范圍內，當模態數由14階增大至16階后，薄膜振幅均值出現陡降，并隨模態數進一步增大保持穩定。因此本文分析薄膜動力學響應時，至少需要取16階模態才能分辨出動力學響應特征。綜合靜力學變形與動力學響應研究需要，以下算例均采用16階模態進行計算。

3 光壓作用下薄膜力學行為

3.1 切向光壓作用下薄膜行為特性

本節僅考察切向光壓力作用下薄膜力學行為特性，忽略式（8）中法向光壓力與熱應力。由于薄膜運動方程式（8）與氣動力作用下壁板運動方程具有相似數學形式，因此本文算例中太陽帆薄膜與壁板具有相似的穩定性邊界特征。當作用于壁板的氣動力大于臨界動壓時，壁板進入動力學顫振。類似地，當作用于薄膜的法向光壓力大于臨界值時，薄膜呈現動力學顫振現象。圖3 給出太陽輻射入射角γ=60°，支桿張力為0 時薄膜振幅的時間響應，此時薄膜在切向光壓力作用下發生顫振。

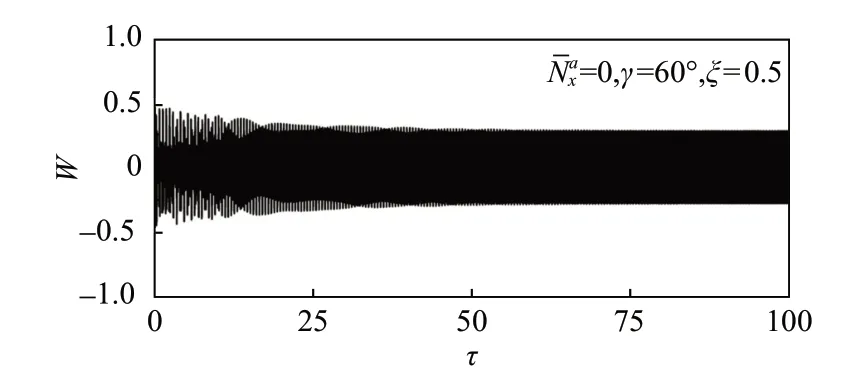
圖3 切向光壓力作用下薄膜動力學顫振Fig.3 Membrane flutter under the tangent solar pressure

3.2 考慮法向光壓的薄膜行為特性

法向光壓在數學形式上等價于氣動彈性問題中壁板所受靜壓差。根據氣動彈性理論，在von Kármán 大變形結構模型中，靜壓差會抑制壁板顫振［6-7］。本節考察法向光壓力對薄膜行為特性影響。

對比無量綱法向光壓力與無量綱切向光壓力

法向光壓與切向光壓比值與薄膜長厚比為同一量級，太陽帆薄膜厚度僅為10 μm 量級，長度為10 m 量級，由式（12）可知，法向光壓約為切向光壓107倍。圖4 給出在相同支桿張力以及太陽輻射入射角條件下，考慮法向光壓作用后薄膜振幅的時間響應。對比圖3 所示算例，薄膜在法向光壓力作用下形成較大幅值靜變形，進而增大薄膜面內力，抑制薄膜顫振。

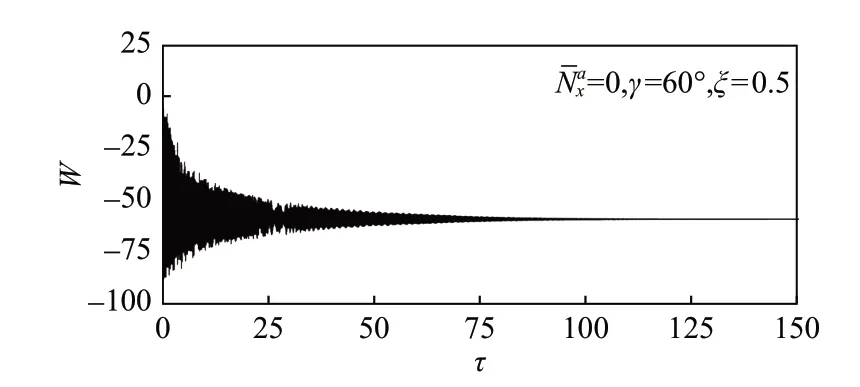
圖4 法向光壓作用下薄膜靜變形Fig.4 Membrane static deformation caused by normal solar pressure

根據式（2）可知，隨著入射角增大，法向光壓力降低，薄膜靜變形幅值減小。對一特殊情況：當入射角達到90°時，法向光壓力為0，薄膜從靜變形轉變為動力學顫振如圖5 所示，此時切向光壓力達到最大，薄膜振幅也相應增大。

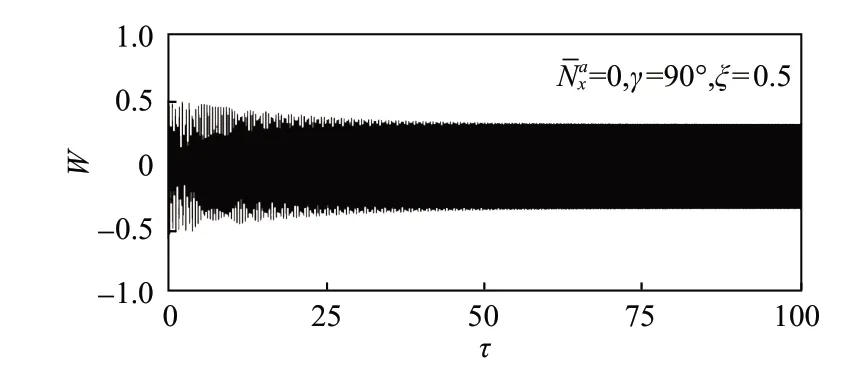
圖5 γ=90°極限條件下太陽帆顫振Fig.5 Membrane flutter under the limit condition γ=90°

由于太陽帆需接受太陽輻射產生有效的光壓推進，一般情況下不會出現入射角等于90°的情況（此時太陽光與薄膜平衡態表面平行），因此在正常運行期間，可認為太陽帆在光壓作用下不發生顫振。

4 熱載荷耦合光壓薄膜行為特性

4.1 切向光壓作用下薄膜行為特性

圖6 給出僅考慮式（8）中切向光壓力與熱應力作用時，薄膜隨太陽輻射通量差ΔS變化分岔特性。如圖所示，隨著輻射通量差逐漸增大，薄膜首先在支桿張力作用下保持穩定，當輻射通量差突破臨界值ΔS=7.5 W/m2后，薄膜在熱載荷誘導下直接形成混沌運動，將該ΔS定義為進入混沌的臨界通量差。圖7 給出此時薄膜混沌運動龐加萊截面圖、最大Lyapunov 指數（LLE）［16］。龐加萊截面圖基于薄膜特定運動狀態取得，此處選取的運動狀態：辨識點（ξ=0.75）由負達到0 時，記錄參考點（ξ=0.5）處的運動狀態。當龐加萊截面圖中一團散點呈特定形態分布時，薄膜進行混沌運動。此外，當LLE 大于零時，表征動力學系統進入混沌運動。如圖7 所示，龐加萊截面圖散點呈“花生米”狀分布；LLE收斂于正數。結合上述特征表明薄膜進入混沌運動。

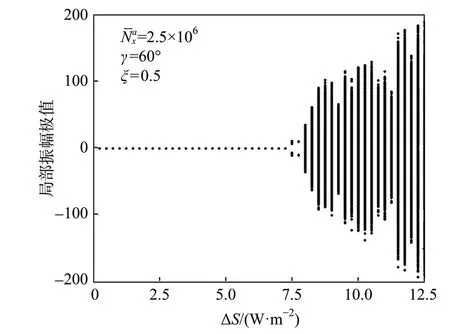
圖6 切向光壓作用下薄膜隨光輻射通量差增大的分岔特性Fig.6 Membrane bifurcation diagram versus increasing thermal load considering tangent solar pressure

受薄膜小厚度影響，薄膜所受熱應力對太陽輻射通量差敏感，當ΔS約為1 W/m2時，作用于薄膜的無量綱熱應力達到106數量級。對比壁板氣動彈性問題，壁板由極限環運動進入混沌運動過程中-變化區間僅為102數量級，遠小于作用于薄膜的無量綱熱應力數量級。因此，圖6 中薄膜倍周期運動，準周期運動等運動區間被壓縮，難以觀測。當ΔS超過進入混沌的臨界通量差后，薄膜直接由靜穩定轉變為混沌運動。

4.2 考慮法向光壓的薄膜行為特性

同時考慮式（8）中切向光壓力、法向光壓力和面內熱應力。如上所述，在法向光壓力作用下，薄膜呈現靜變形。圖8進一步對比有、無熱載荷條件下，薄膜靜變形幅值，其中太陽輻射通量差ΔS=0 W/m2時，對應熱載荷為0。由圖8 可知，隨著熱載荷增大，薄膜剛度減弱［22-23］，靜變形程度增大。

與切向光壓作用下薄膜行為特性類似，隨著熱載荷逐漸增大并超過進入混沌的臨界通量差，薄膜在熱載荷誘導下由靜變形轉變為混沌運動。圖9給出當ΔS進一步增大至27.5 W/m2時，薄膜混沌運動龐加萊截面圖和LLE 收斂曲線。圖中龐加萊截面圖一團散點呈橢圓狀分布，LLE 收斂于正數。結合上述特征表明薄膜進入混沌運動。綜上所述，即使存在法向光壓力抑制薄膜振動，當ΔS超過進入混沌的臨界通量差后，薄膜轉變為混沌運動。與僅考慮切向光壓作用相比，計及法向光壓作用后，薄膜進入混沌的臨界通量差有明顯增大。

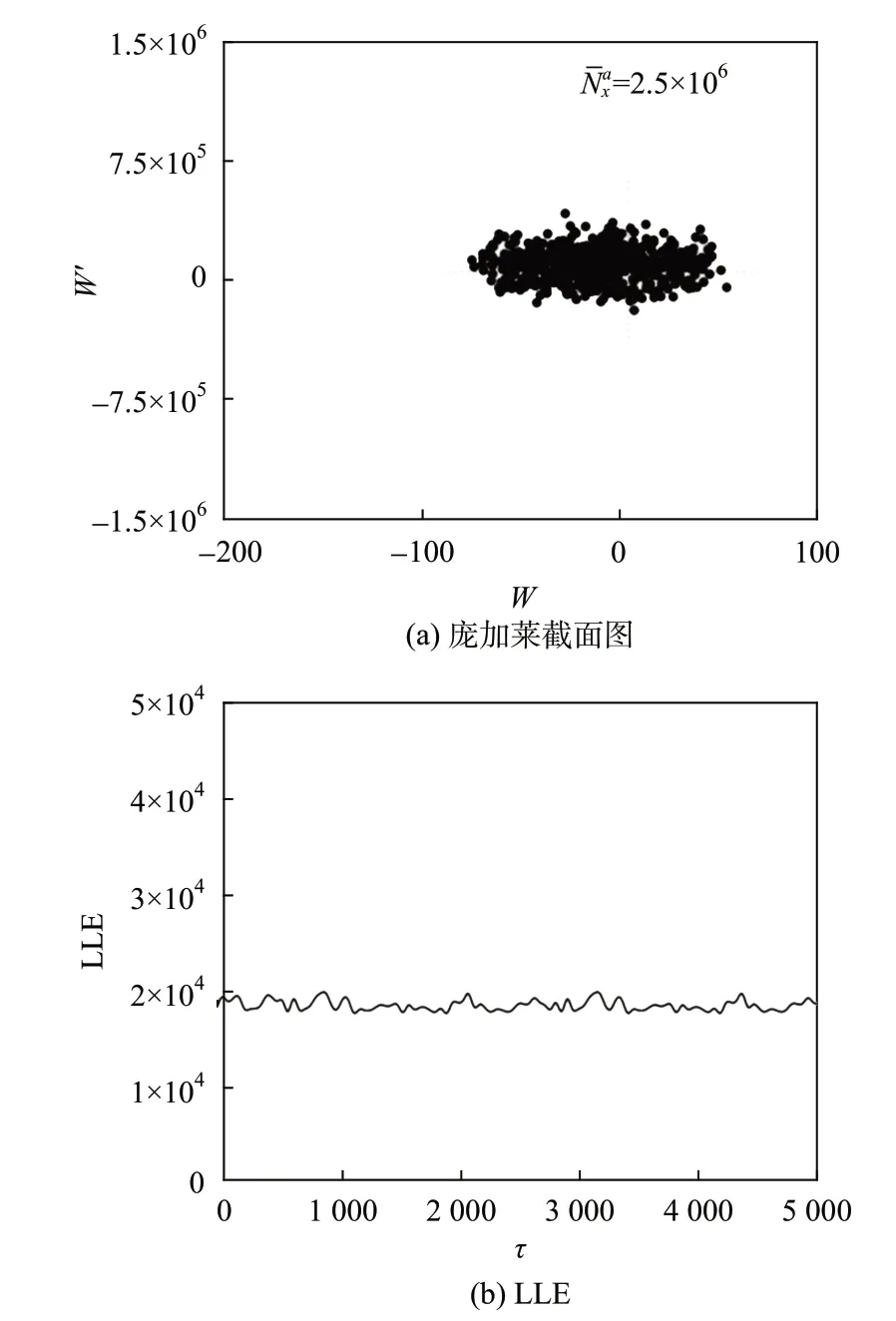
圖9 考慮法向光壓作用下薄膜混沌運動（ΔS=27.5 W/m2，γ=60°）Fig.9 Membrane chaotic motion considering normal solar pressure（ΔS=27.5 W/m2，γ=60°）

5 結論

基于von Kármán 大撓度理論計及太陽帆薄膜形變的幾何非線性，考察薄膜在切向光壓力、法向光壓力以及考慮熱載荷后薄膜的力學行為特性。主要結論如下：

1）僅考慮切向光壓力時，薄膜在切向光壓力作用下顫振。當計及法向光壓力作用后，薄膜呈現靜變形；僅當太陽輻射入射角達到90°極限條件時，法向光壓力為0，此時薄膜呈現動力學顫振。

2）存在臨界光輻射通量差，當熱載荷大于臨界輻射通量差后，激發薄膜混沌運動。法向光壓力能夠增大進入混沌的臨界通量差。

3）模態收斂數與薄膜行為特性相關。當薄膜呈現靜變形時，4 階模態計算結果收斂；當薄膜進入動力學混沌運動時，至少取16階模態才可分辨薄膜動力學特性。

作用于太陽帆薄膜的法向光壓力遠大于切向光壓力，考慮法向光壓力抑制作用后，太陽帆薄膜不會顫振。光輻射熱載荷激發薄膜混沌運動。文中光輻射熱載荷未與薄膜形變耦合，熱載荷耦合薄膜形變后的薄膜響應需進一步研究。