考慮用戶能動性和流動性的輿情傳播模型

馬源源，解蕾蕾，董 南，劉 娜

（1.東北大學(xué) 工商管理學(xué)院，沈陽 110819；2.東北大學(xué)秦皇島分校 經(jīng)濟(jì)學(xué)院，河北 秦皇島 066004；3.東北大學(xué)秦皇島分校 管理學(xué)院，河北 秦皇島 066004）

0 引言

隨著互聯(lián)網(wǎng)的發(fā)展，社會突發(fā)事件通過各種渠道進(jìn)行廣泛傳播［1］已經(jīng)成為網(wǎng)絡(luò)輿情的焦點(diǎn)。然而，有些信息與事實相違背，一些所謂的“媒體人”覬覦流量的好處，利用這些虛假的信息達(dá)到自己的目的。尤其是在疫情爆發(fā)期間，謠言傳播造成了公眾的恐慌和社會的不穩(wěn)定。因此，在突發(fā)事件發(fā)生后，快速識別輿情傳播的演化趨勢，分析影響輿情傳播的機(jī)制，對于官方制定應(yīng)急方案具有重要意義。

由于輿情傳播與傳染病傳播非常相似，許多學(xué)者借鑒生物學(xué)意義上的倉室模型研究輿情傳播動力學(xué)模型［2-4］。盡管上述模型模擬了不同群體在社交網(wǎng)絡(luò)中的傳播過程，但并沒有考慮個人行為和人際關(guān)系對輿情傳播的影響。考慮到用戶的感知行為，Sang 等［5］表明可以通過提高用戶意識抑制謠言的傳播。此外，用戶的行為也受到情感傾向和心理因素的影響。Xiao 等［6］考慮了用戶的從眾心理，但對于同一熱門話題，網(wǎng)民的心理活動是錯綜復(fù)雜的。網(wǎng)民聽到話題時通常會發(fā)揮主觀能動性，具體表現(xiàn)為3 種行為：1）相信流言，成為傳播者；2）先評論然后觀望周遭環(huán)境；3）主動防御，不參與話題的傳播。同時，在作出行為決策中通常伴隨著各種心理活動，典型的就是追根溯源的好奇心理和從眾心理。本文將綜合用戶的行為和心理反應(yīng)兩方面衡量用戶的能動性，以構(gòu)建一個更加符合現(xiàn)實規(guī)律的輿情傳播模型。

用戶的流動性也是影響社交網(wǎng)絡(luò)中輿情傳播的一個重要因素。先前關(guān)于輿情傳播動力學(xué)的研究主要集中于靜態(tài)網(wǎng)絡(luò)結(jié)構(gòu)［7-8］，沒有考慮用戶的遷入與遷出。它們只能模擬傳播時間較短的輿情傳播過程，局限性顯而易見。由于虛擬的網(wǎng)絡(luò)環(huán)境，人們可以自由選擇離開或留下，這是在線社交網(wǎng)絡(luò)中普遍存在的現(xiàn)象，因此考慮用戶總數(shù)變化對輿情傳播的影響是必要的。

以上討論都是基于模型構(gòu)建的合理性，往往控制負(fù)面輿論的傳播也很關(guān)鍵。Xia 等［9］通過最優(yōu)控制方法提出了遏制謠言傳播的一系列控制策略。目前，最優(yōu)控制大都針對單個參數(shù)進(jìn)行研究［10-11］，而現(xiàn)實生活中謠言的控制需要多方共同的努力，因此，將引入多重控制機(jī)制進(jìn)行研究。

上述模型僅從理論上分析了輿情傳播的規(guī)律，但大多數(shù)模型并未結(jié)合真實數(shù)據(jù)進(jìn)行驗證。隨著大數(shù)據(jù)技術(shù)的普及，獲取社交媒體上的用戶生成內(nèi)容（User Generated Content，UGC）越來越容易。近來，有學(xué)者使用真實數(shù)據(jù)集構(gòu)建實際傳播網(wǎng)絡(luò)，并基于此考察信息的真實傳播情況［12］。Yin等［13-15］研究了信息交叉?zhèn)鞑ピ谛鹿诜窝字械挠绊懀⑹褂眯吕宋⒉┑恼鎸崝?shù)據(jù)驗證有效性。本文爬取新浪微博上的熱點(diǎn)話題，并利用最小二乘法驗證模型的可靠性。

在上述分析和文獻(xiàn)［5］的啟發(fā)下，本文提出SCBRD（Susceptible-Commented-Believed-Recovered-Defensed）輿情傳播模型。本文的主要工作如下：

1）將用戶能動性和流動性納入輿情傳播模型，在更復(fù)雜的網(wǎng)絡(luò)結(jié)構(gòu)上探究用戶行為和心理對輿情傳播的影響。

2）計算模型的平衡點(diǎn)和基本再生數(shù)，分析了復(fù)雜網(wǎng)絡(luò)的動力學(xué)行為，并通過引入多重控制機(jī)制求得總成本最小條件下的控制解。

3）與大多數(shù)現(xiàn)有研究不同，本文基于新浪微博的真實數(shù)據(jù)驗證模型的有效性，并采用最小二乘法估計模型參數(shù)，以準(zhǔn)確預(yù)測輿情的傳播趨勢。

1 模型的建立與分析

1.1 模型建立

傳統(tǒng)的SIR（Susceptible-Infected-Recovered）輿情傳播模型將人群分成易感者（S）、感染者（I）和免疫者（R）三類。在社交媒體上，用戶具有能動性行為。本文在傳統(tǒng)模型的基礎(chǔ)上，將感染者（I）細(xì)分為相信者（B）和評論者（C），并增加了主動防御者（D）。其中，相信者和評論者體現(xiàn)了用戶能動地參與信息傳播的過程；主動防御者體現(xiàn)了用戶發(fā)揮主觀能動意識，盡可能地避免信息的傳播。

結(jié)合社交媒體的傳播機(jī)制，感染行為可以分為轉(zhuǎn)發(fā)和評論兩種。以新浪微博為例，當(dāng)輿論話題盛行時，《人民日報》《新華網(wǎng)》和許多大V 博主均會發(fā)布。相信該話題的用戶最有可能轉(zhuǎn)發(fā)該微博，該轉(zhuǎn)發(fā)行為直接影響著信息的傳播；而對該話題遲疑但又感興趣的用戶最有可能先是評論，然后觀摩周遭環(huán)境，隨時可能轉(zhuǎn)換為傳播者，該評論行為間接影響信息的傳播。還有一類理性程度較高的用戶，可以理解為高級的理性知識分子，他們會主觀判斷信息的真?zhèn)位騼r值，但不會參與信息的傳播。總之，用戶在接收到消息時通常會發(fā)揮主觀能動性并表現(xiàn)于行為決策。同時，在線社交網(wǎng)絡(luò)中用戶可以隨時地發(fā)表見解和看法，自由地參與或離開某個話題的討論，充分體現(xiàn)了流動性。

根據(jù)上述分析，提出了一個動態(tài)的SCBRD 輿情傳播模型，將從用戶的意識行為和心理反應(yīng)兩方面考量用戶的能動性。假設(shè)每個用戶是異構(gòu)網(wǎng)絡(luò)中的一個節(jié)點(diǎn)，社交網(wǎng)絡(luò)中節(jié)點(diǎn)在時間t的總數(shù)用N(t)表示，可以分為5 類：Sk(t)、Ck(t)、Bk(t)、Rk(t)、Dk(t)分別表示在時間t度數(shù)為k的易感節(jié)點(diǎn)、評論節(jié)點(diǎn)、相信節(jié)點(diǎn)、免疫節(jié)點(diǎn)、防御節(jié)點(diǎn)數(shù)。社交網(wǎng)絡(luò)中每個用戶在任一時刻僅處于一種狀態(tài)，用戶的狀態(tài)隨時間變化，且轉(zhuǎn)換規(guī)則遵循如下：

1）對于易感人群，當(dāng)聽到話題時，通常會發(fā)揮主觀能動性表現(xiàn)為3 種意識行為且伴隨一定程度的好奇心理：①主動防御意識行為，也就是Sk(t) →Dk(t)過程。若用戶的知識儲備豐富，他們會以ε的概率主動判斷信息真?zhèn)危也粫绊懫渌脩舻倪x擇。②評論行為，也就是Sk(t) →Ck(t)過程。由于用戶分析能力不強(qiáng)，不能果斷做出選擇，而是出于強(qiáng)烈的好奇心，選擇先以現(xiàn)有的知識和經(jīng)驗進(jìn)行評論。③轉(zhuǎn)發(fā)行為，也就是Sk(t) →Bk(t)過程。有一部分用戶同樣保持著好奇的心理，以λ的概率轉(zhuǎn)發(fā)流言，并通過社交網(wǎng)絡(luò)傳播給其他人。

2）由于評論者的搖擺不定，當(dāng)再次看到信息時，很容易受到周圍人的影響，并伴隨一定的從眾心理：①Ck(t) →Bk(t)過程中，“羊群效應(yīng)”發(fā)揮作用，評論者以βh的概率轉(zhuǎn)化為相信者，進(jìn)一步傳播流言；②Ck(t) →Rk(t)過程中，由于周圍人興趣減少或遺忘，他們會以β(1 -h)的概率轉(zhuǎn)化為免疫者，抑制信息的傳播。

3）在政府的干預(yù)下，傳播者會以δ的概率轉(zhuǎn)化為免疫者，體現(xiàn)了Bk(t) →Rk(t)過程。隨著免疫者知識和經(jīng)驗的增長，他們會具備不主動擴(kuò)散不實信息的意識，以η概率轉(zhuǎn)化為防御者，對應(yīng)Rk(t) →Dk(t)過程。

那么，一條信息在系統(tǒng)內(nèi)傳播時，用戶的能動性主要表現(xiàn)為轉(zhuǎn)發(fā)、評論和主動防御3 種意識行為和好奇、從眾2 類心理反應(yīng)。用戶的流動性與在線社交網(wǎng)絡(luò)的動態(tài)性恰好對應(yīng)，反映在進(jìn)入率p和離開率d。假設(shè)初始時刻，系統(tǒng)內(nèi)全為易感者。根據(jù)以上傳播準(zhǔn)則，SCBRD 輿情傳播模型的傳播過程如圖1 所示。模型中的參數(shù)均為0～1 的正數(shù)，具體含義的解釋見表1。

表1 SCBRD模型中各參數(shù)的含義Tab.1 Meanings of parameters in SCBRD model

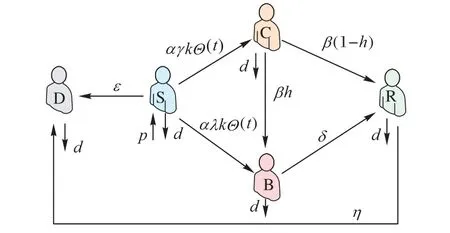
圖1 SCBRD輿情傳播模型的狀態(tài)轉(zhuǎn)換Fig.1 State transition of SCBRD opinion propagation model

此外，SCBRD 模型在平均場方程水平下近似滿足以下一組耦合微分方程：

其中k=1，2，…，n代表著無標(biāo)度網(wǎng)絡(luò)的度值。Θ(t)表示易感節(jié)點(diǎn)和感染節(jié)點(diǎn)之間的平均連接數(shù)，即

其中p(j|k)是指一個度數(shù)為k的節(jié)點(diǎn)連接到另一個度數(shù)為j的節(jié)點(diǎn)的條件概率，并且

1.2 基本再生數(shù)和平衡點(diǎn)的存在性

定理1如果SCBRD 系統(tǒng)存在一個無流言平衡點(diǎn)E0=那么該系統(tǒng)的基本再生數(shù)為：

一般來說，R0的求解方法有4 種［17］，分別從定義、初始時刻染病者的單調(diào)性、正平衡點(diǎn)的存在性和無病平衡點(diǎn)的局部穩(wěn)定性這4 個角度導(dǎo)出。其中定義法僅適用于比較簡單的模型；第二種方法需要對初始時刻的易感者近似取值；第三種方法只能證明均衡點(diǎn)的存在性，不能說明它可作為判斷爆發(fā)與否的充要條件。這三種方法只是對基本再生數(shù)的粗略估計，而根據(jù)無病平衡點(diǎn)的局部穩(wěn)定性能計算得到精確的R0表達(dá)式。考慮到相對復(fù)雜的系統(tǒng)，在第三種方法的基礎(chǔ)上改進(jìn)并提出了下一代矩陣的方法。其次，利用下一代矩陣法［18］求解基本再生數(shù)R0。令χ=(Sk(t)，Ck(t)，Bk(t)，Rk(t))，SCBRD 模型化簡為：

在E0處，F(xiàn)(χ)，V(χ)的雅克比矩陣為：

基本再生數(shù)R0表示易感人群看到評論和轉(zhuǎn)發(fā)之后被感染的人數(shù)［18-19］。定義R0=ρ(fv-1)，其中ρ(fv-1)是再生矩陣fv-1的光譜半徑。通過計算，可得到式（5）。R0=1是區(qū)分輿論是否爆發(fā)的閾值，在動力學(xué)系統(tǒng)的分析中非常重要。

定理2如果R0>1，SCBRD 模型有且存在唯一的流言持續(xù)平衡點(diǎn)

證明 令式（1）右邊等于0，可求得在流言持續(xù)平衡點(diǎn)處各節(jié)點(diǎn)的等式關(guān)系為：

這證明了流言持續(xù)平衡點(diǎn)的存在性。接下來，要證明它的唯一性。那么，構(gòu)造如下輔助函數(shù)：

對上述等式右邊取極限，可以得到如下結(jié)果：

由介值定理得，F(xiàn)(Θ*)=0 定義域上有且僅有一個正數(shù)解，那么有唯一的解，進(jìn)而推出其他節(jié)點(diǎn)也僅有唯一的正數(shù)解。至此，流行持續(xù)平衡點(diǎn)的唯一性得以證明。因此，如果R0>1，SCBRD 模型有且存在唯一的流言持續(xù)平衡點(diǎn)。

備注 為驗證基本再生數(shù)計算的準(zhǔn)確性，本文根據(jù)流言平衡點(diǎn)的存在性再次計算了基本再生數(shù)R0。

顯然，Θ=0 是上述自治方程的一個解。為此，構(gòu)造函數(shù)H(Θ)=Θ-f(Θ)，其中f(Θ)可表示為：

通過了解H(Θ)的函數(shù)性質(zhì)，可知其為凹函數(shù)。此外，為保證函數(shù)H(Θ)在0 <Θ<1 有解，則H(Θ)關(guān)于Θ的導(dǎo)數(shù)需滿足：

因此，得到系統(tǒng)（1）的基本再生數(shù)為式（5）。此時，基本再生數(shù)的值與下一代矩陣方法的結(jié)果是一致的，進(jìn)一步驗證了基本再生數(shù)R0的正確性。

1.3 動力學(xué)分析

定理3當(dāng)R0<1 時，SCBRD 模型在無流言平衡點(diǎn)處是全局漸近穩(wěn)定的，否則是不穩(wěn)定的。

證明 為了證明其全局漸近穩(wěn)定性，定義

其中：Ck(t)、Bk(t)均為正數(shù)，其余參數(shù)均位于[0，1]。Vk(t)滿足無限大正定的要求，因此，它是Lyapunov 函數(shù)。通過Vk(t)對t求導(dǎo)，可得：

根據(jù)LaSalle 不變集原理［20］，當(dāng)R0<1 時，Bk(t)(R0-1) ≤0。此時，SCBRD模型在無流言平衡點(diǎn)處是全局漸近穩(wěn)定的。

通過數(shù)值模擬驗證上述結(jié)論，給定參數(shù)p=0.1，d=0.15，α=0.3，γ=0.2，λ=0.2，β=0.2，h=0.2，δ=0.2，ε=0.12，η=0.1。此時，簡單計算可得到R0=0.322 1 <1，SCBRD 模型的演化趨勢顯示在圖2 中。由圖2 可知，系統(tǒng)中感染人群的密度趨近于0，表明系統(tǒng)（1）存在無流言平衡點(diǎn)，且全局漸近穩(wěn)定。此時，易感節(jié)點(diǎn)和防御節(jié)點(diǎn)會趨近于一個正常數(shù)，相信節(jié)點(diǎn)和評論節(jié)點(diǎn)（可統(tǒng)稱為感染節(jié)點(diǎn)）會趨于0，在線社交網(wǎng)絡(luò)中不會存在該話題的持續(xù)傳播。

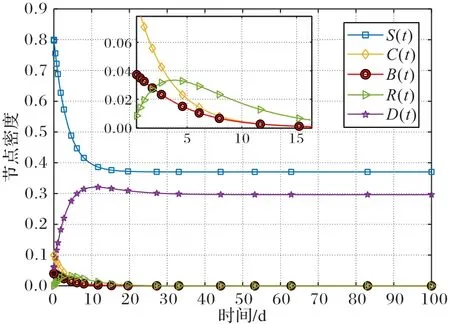
圖2 R0 <1時SCBRD系統(tǒng)的時間序列軌跡圖Fig.2 Time series trajectories of SCBRD system when R0 <1

定理4當(dāng)R0>1 時，SCBRD 模型在流言持續(xù)平衡點(diǎn)處是全局漸近穩(wěn)定的。

證明 引入函數(shù)g(x)=x-1 -lnx，x>0。在x=1 時，g(1)=0。該函數(shù)在整個區(qū)間內(nèi)呈現(xiàn)先減后增的趨勢，且在x=1 時取得最小值。

接著，構(gòu)造無限大正定的Lyapunov 函數(shù)Vk(t)，定義為：

對Vk(t)求導(dǎo)可得：

參考文獻(xiàn)［20］，選擇合適的ρ1、ρ2，則ρ1、ρ2需要滿足如下關(guān)系：

此時Vk'(t) ≤0。同樣地，根據(jù)LaSalle 不變原理，如果R0>1，系統(tǒng)在平衡點(diǎn)處全局漸近穩(wěn)定。也就是說，系統(tǒng)趨于穩(wěn)定時，社交網(wǎng)絡(luò)中的相關(guān)輿論話題會廣泛傳播，最終會形成熱點(diǎn)話題并廣為人知。為驗證這一結(jié)論，給定仿真參數(shù)p=0.18，d=0.1，α=0.2，γ=0.5，λ=0.6，β=0.4，h=0.3，δ=0.01，ε=0.05。此時的基本再生數(shù)R0=7.153 0 >1，相應(yīng)的變化趨勢顯示在圖3 中。

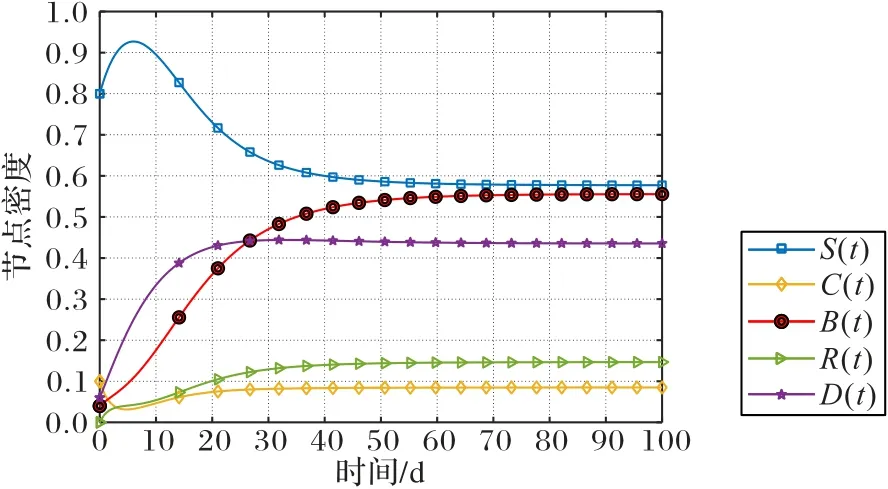
圖3 R0 >1時SCBRD系統(tǒng)的時間序列軌跡圖Fig.3 Time series trajectories of SCBRD system when R0 >1

圖3 中易感節(jié)點(diǎn)的密度曲線呈現(xiàn)出先升后降的趨勢，其余4 類節(jié)點(diǎn)密度的曲線均表現(xiàn)為逐步增加。當(dāng)系統(tǒng)穩(wěn)定時，社交網(wǎng)絡(luò)上不斷出現(xiàn)轉(zhuǎn)發(fā)、評論等感染性行為，形成大規(guī)模輿論狂潮。因此，R0的變化會導(dǎo)致系統(tǒng)內(nèi)各類人群發(fā)生顯著性變化，調(diào)控R0的大小也就成為輿情監(jiān)控的最有效手段。

2 數(shù)值仿真分析

對于本文提出的SCBRD 模型，在第1 章已經(jīng)利用解析分析的方法從理論上研究了系統(tǒng)的動力學(xué)行為。為了深入探討輿情傳播機(jī)制，有必要分析該系統(tǒng)各個參數(shù)的影響。從基本再生數(shù)R0的表達(dá)式可以看出，R0的大小與參數(shù)α、β、λ、γ、h、ε、δ、p、d有關(guān)。接下來，將分組進(jìn)行關(guān)鍵參數(shù)和R0的敏感性分析。最后，考慮到社交網(wǎng)絡(luò)中用戶個體之間的異質(zhì)性，分析了網(wǎng)絡(luò)度值k的影響。

文獻(xiàn)［21］研究表明，社交網(wǎng)絡(luò)最接近于無標(biāo)度網(wǎng)絡(luò)，通過構(gòu)造度分布服從p(k)=cγk-γ的無標(biāo)度網(wǎng)絡(luò)對SCBRD 系統(tǒng)進(jìn)行仿真分析，其中：γ為無標(biāo)度網(wǎng)絡(luò)的冪律指數(shù)，這里選擇γ=3［5］；k為無標(biāo)度網(wǎng)絡(luò)的度值。無標(biāo)度網(wǎng)絡(luò)中的總節(jié)點(diǎn)數(shù)N=1 000［21］，常數(shù)cγ滿足系 統(tǒng)中其他參數(shù)均為概率值，即它們符合的范圍為［0，1］。根據(jù)文獻(xiàn)［9，16，22-23］中設(shè)定的參數(shù)區(qū)間范圍，本章按要求選擇了不同的參數(shù)取值，結(jié)果顯示在表2 中。此外，對每類節(jié)點(diǎn)數(shù)加權(quán)求和并進(jìn)行歸一化處理，得到它們在每一時刻的密度。設(shè)定在初始時刻，各類節(jié)點(diǎn)的密度分別為Sk(0)=0.8，Ck(0)=0.1，Bk(0)=0.04，Rk(0)=0，Dk(0)=0.06。下面將利用敏感性分析和四階Runge-Kutta 法［24］詳細(xì)討論SCBRD 系統(tǒng)的性質(zhì)。

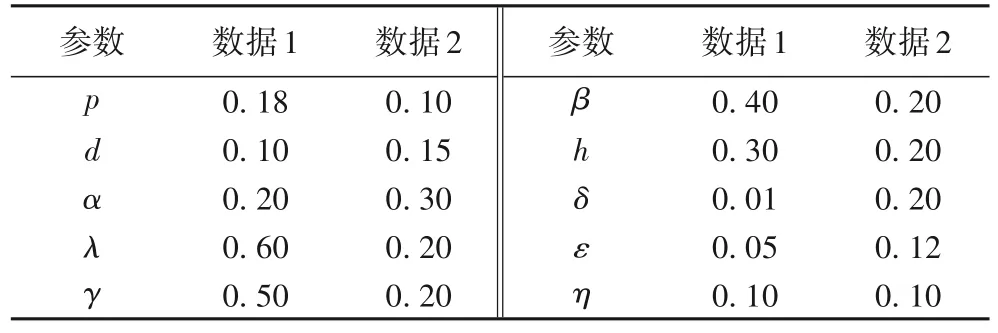
表2 敏感性分析的參數(shù)Tab.2 Parameters for sensitivity analysis

2.1 用戶能動性對閾值的影響

當(dāng)易感者聽到熱點(diǎn)話題時，通常會發(fā)揮主觀能動性。本節(jié)將具體討論這些能動性表現(xiàn)中哪些在輿情傳播過程中更突出。

首先，將反映好奇心理的參數(shù)α、反映從眾心理的參數(shù)h和被感染的概率β分為一組。選擇數(shù)據(jù)1 并且使得α、h在區(qū)間［0，1］上任意取值，得到R0與α、h的關(guān)系顯示在圖4（a）。類似地，用數(shù)據(jù)2 繪制圖4（b）、圖4（c）。

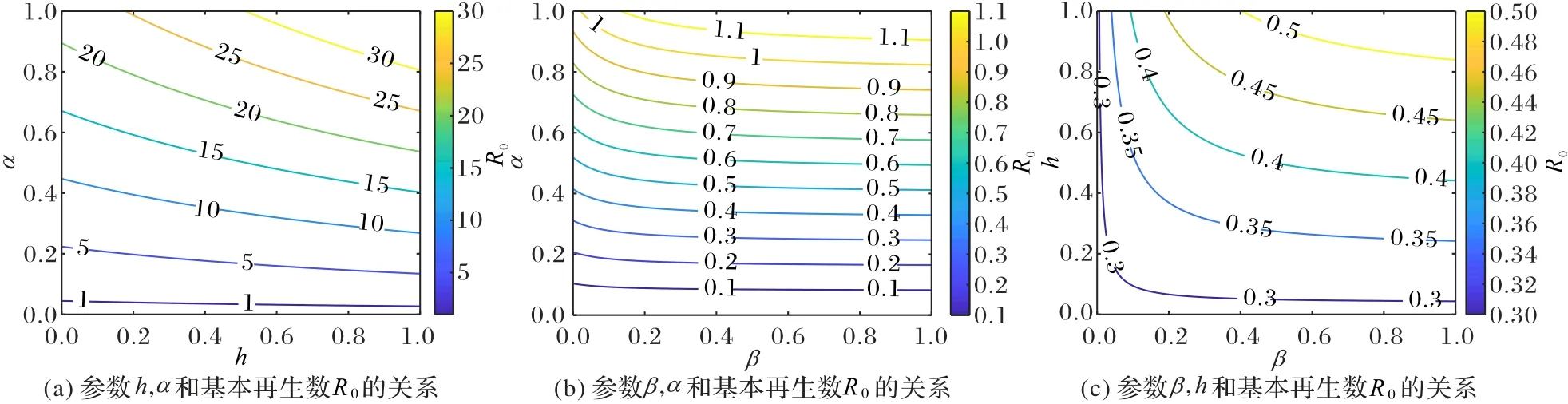
圖4 基本再生數(shù)R0對α，h，β的靈敏度分析Fig.4 Sensitivity analysis of basic reproduction number R0 to α，h，β

把R0看作參數(shù)α、h、β的函數(shù)，那么存在如下的關(guān)系：

由此可得到基本再生數(shù)R0與3 個參數(shù)均為正相關(guān)關(guān)系。

從圖4 可以看出，隨著α、h、β的增大，基本再生數(shù)R0也逐漸增大，該結(jié)果與理論分析一致。此外，α比h引起的閾值變化范圍更大，這說明基本再生數(shù)R0對反映好奇心理的參數(shù)α更敏感，揭示了在輿情傳播過程中，用戶的好奇心理比從眾心理扮演著更重要的角色。結(jié)合圖4（b）和（c），可以得到基本再生數(shù)R0對好奇心理h最敏感，并且3 個參數(shù)對閾值的影響均為非線性的。因此，對于負(fù)面輿情話題，官方應(yīng)盡可能地提供更多可靠的線索，減少網(wǎng)民的好奇心理以營造積極健康的社交網(wǎng)絡(luò)環(huán)境。

其次，將反映意識行為的參數(shù)λ、γ、ε分為一組，對比分析哪種意識行為對輿論傳播的影響最大。選擇數(shù)據(jù)1 繪制得到R0與λ、γ、ε的關(guān)系，結(jié)果顯示在圖5 中。

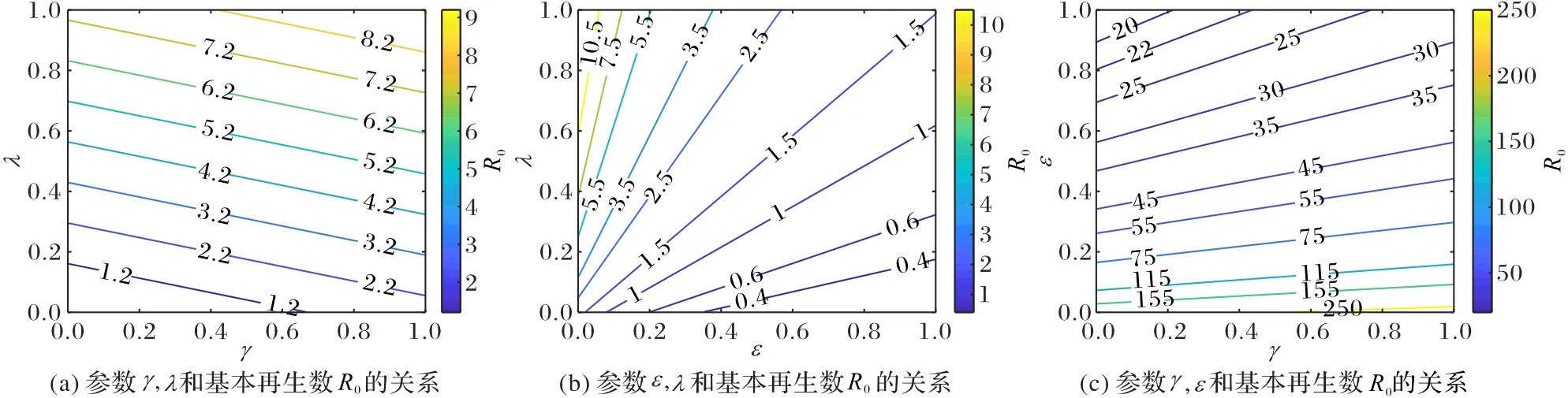
圖5 基本再生數(shù)R0對λ，γ，ε的靈敏度分析Fig.5 Sensitivity analysis of basic reproduction number R0 to λ，γ，ε

注意到：

那么基本再生數(shù)R0與λ、γ成正相關(guān)，而與參數(shù)ε成負(fù)相關(guān)關(guān)系。

觀察圖5 可知，參數(shù)λ、γ、ε與基本再生數(shù)R0均成線性關(guān)系。在等間隔的變化中，λ會引起R0較大的變化，說明轉(zhuǎn)發(fā)率λ比評論率γ更容易掀起輿論熱潮。這與現(xiàn)實情況類似，往往身邊的朋友轉(zhuǎn)發(fā)微博比評論微博更能引起注意。圖5（b）中，當(dāng)R0>1.5 時，基本再生數(shù)R0對λ更敏感；且在ε較小時，它的敏感性程度要比ε值大時更明顯。這意味著當(dāng)不利輿論泛濫時，轉(zhuǎn)發(fā)意識行為占據(jù)主導(dǎo)地位，并隨著主動防御意識的提高，轉(zhuǎn)發(fā)行為的敏感性程度越來越低。

由此可見，主動防御意識行為在信息傳播過程中起著一定的作用，但通常用戶具備較強(qiáng)的主動防御意識才能凸顯出其重要性，這勢必會帶來高成本的培訓(xùn)和宣傳費(fèi)用。很容易看出，圖5（c）中參數(shù)ε比γ會引起閾值更大的變動范圍。綜合來講，三種意識行為中評論行為最不容易引起輿論的廣泛傳播，轉(zhuǎn)發(fā)行為通常會帶動話題的熱度。

2.2 用戶流動性對閾值的影響

在線社交網(wǎng)絡(luò)是一個開放系統(tǒng)，用戶的流動性是其特有屬性。為了探討這一特征對輿情傳播的影響，選擇數(shù)據(jù)1研究R0和進(jìn)入率p、離開率d的關(guān)系，可視化結(jié)果顯示在圖6中。

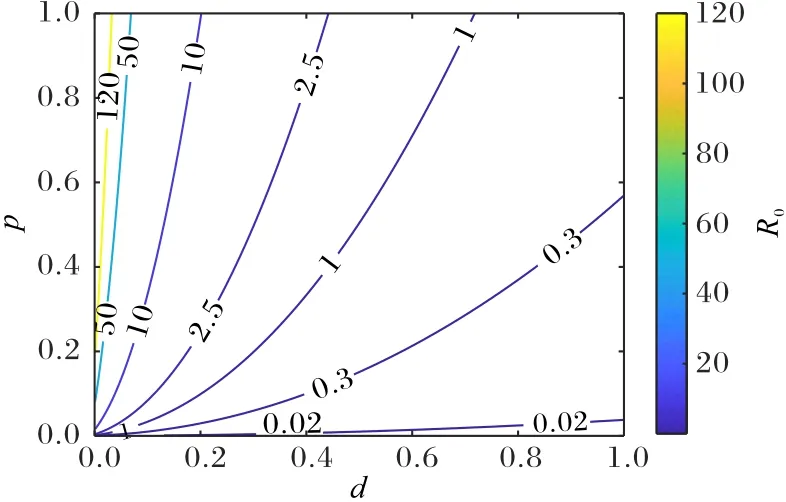
圖6 基本再生數(shù)R0對p，d的靈敏度分析Fig.6 Sensitivity analysis of basic reproduction number R0 to p，d

可以看到p和R0是正線性相關(guān)的，而d和R0是負(fù)非線性相關(guān)的。在等同條件［0，1］內(nèi)變化時，進(jìn)入率引起的變化范圍大于離開率引起的變化范圍。此外，在R0=1 時，臨界值為p=0.094，d=0.187。比較發(fā)現(xiàn)，p比d會造成更大的閾值變化。這意味著在處理負(fù)面輿情時，控制進(jìn)入率通常比增加離開率更有效。

2.3 無標(biāo)度網(wǎng)絡(luò)度值k的影響

在社交網(wǎng)絡(luò)中，每個用戶都存在差異，這種差異性也會影響著輿情傳播的特征。考慮到復(fù)雜網(wǎng)絡(luò)的異質(zhì)性，度值k表示無標(biāo)度網(wǎng)絡(luò)中相鄰節(jié)點(diǎn)連接邊數(shù)，一定程度上反映了社交網(wǎng)絡(luò)的復(fù)雜性。選擇數(shù)據(jù)1，其中度k值取值為1、10、50、100、500，探討不同k取值范圍下各節(jié)點(diǎn)密度的變化趨勢，結(jié)果顯示在圖7 中。

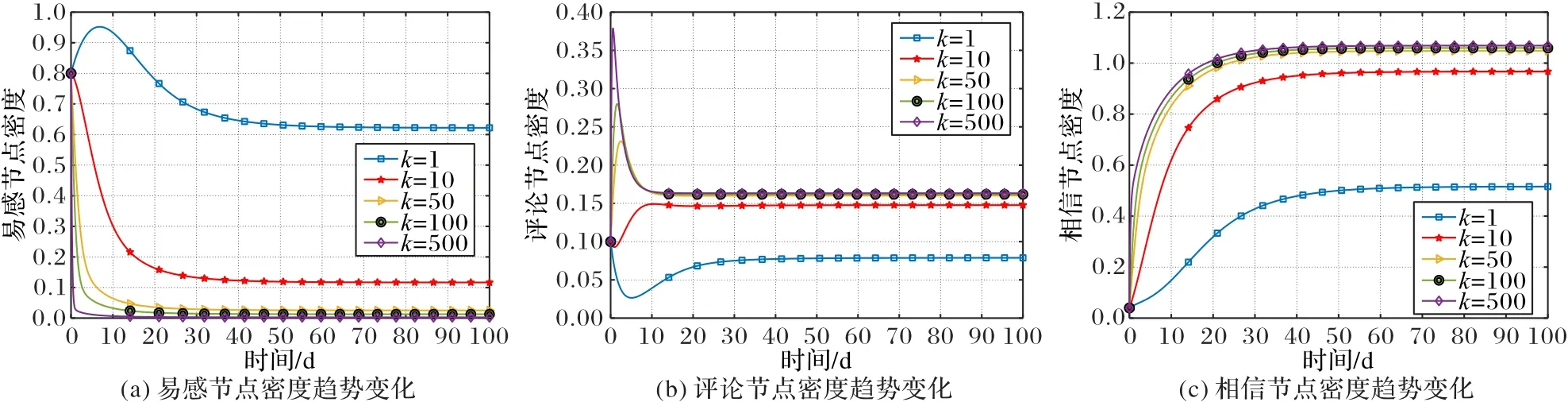
圖7 不同節(jié)點(diǎn)在不同k值的節(jié)點(diǎn)密度趨勢Fig.7 Trends of node density for different nodes with different values of k

正如圖7 所示，度值k=1 的曲線與其他度值的曲線略有不同。原因可能是k太小，此時的社交網(wǎng)絡(luò)比較簡單，人際關(guān)系網(wǎng)對輿情傳播系統(tǒng)的影響較小。隨著易感人群度值k的增大，個體密度逐漸減小，且能達(dá)到的最值越來越小；對于評論人群，人群密度曲線由谷形變?yōu)榉逍吻襨值越大，峰值越大；相信節(jié)點(diǎn)的密度呈現(xiàn)出先上升后穩(wěn)定的趨勢。綜上，度值k越大，系統(tǒng)內(nèi)參與輿論傳播的人數(shù)越多，輿論爆發(fā)的規(guī)模越大，輿論得到了廣泛傳播。此外，度k值的變化并不影響系統(tǒng)的穩(wěn)定性。k值在較小的情況下，變動范圍比較明顯，尤其在區(qū)間［1，10］最明顯。這反映了社交網(wǎng)絡(luò)平臺上，如果某話題的熱度越高，呈現(xiàn)出的網(wǎng)絡(luò)關(guān)系比較復(fù)雜，相關(guān)輿情也會得到廣泛傳播，與實際情況也符合。

3 最優(yōu)控制

對于負(fù)面輿情的傳播，控制目標(biāo)是在考慮控制成本的同時，降低謠言感染者的數(shù)量。在現(xiàn)實生活中，謠言的控制通常是多方努力的結(jié)果。一方面，需要在線社交網(wǎng)絡(luò)中用戶行為的規(guī)范。根據(jù)第2 章敏感性分析結(jié)果，用戶的能動性行為中轉(zhuǎn)發(fā)行為λ最為突出，而心理反應(yīng)也是通過個體的行為決策來表現(xiàn)；用戶的流動性中進(jìn)入率p往往比離開率更加敏感。另一方面，需要的是政府和官方媒體在辟謠和宣傳方面做出的努力δ。鑒于此，將三重控制機(jī)制引入傳播模型，利用龐特里亞金極值原理［24］求解最優(yōu)控制解pku、λku和δku。

為此，引入一個Lebesgue 平方可積控制函數(shù)uku(t)=(pku(t)，λku(t)，δku(t)) ∈U。其中1 -pku(t)是衡量平臺通過撤掉熱搜、刪除話題帖子等手段減少進(jìn)入輿情傳播系統(tǒng)人數(shù)的指標(biāo)，1 -λku(t)表示官方為關(guān)閉社交媒體中的轉(zhuǎn)發(fā)機(jī)制而付出的代價，δku(t)代表著政府為抑制謠言傳播做出的努力。U={ukumeasurable：0 ≤uku≤1}，t∈[0，T]代表控制策略施加在SCBRD系統(tǒng)上的時間周期。那么，新的最優(yōu)控制系統(tǒng)為：

現(xiàn)在，考慮一個帶有最小化目標(biāo)函數(shù)的最優(yōu)控制問題。

式中：J(u)表示政府和官方媒體在規(guī)定時間內(nèi)控制負(fù)面輿情傳播所需的成本費(fèi)用；W1k、W2k和W3k是權(quán)重因子，衡量單個控制策略的成本在總投入中的比例；控制變量的平方（如反映了相應(yīng)控制規(guī)模的重要性。為實現(xiàn)這一目標(biāo)，給出以下拉格朗日函數(shù)：

控制系統(tǒng)的哈密頓能量函數(shù)為：

其中φik(t)(i=1，2，3，4，5)是連接函數(shù)。

為了確定伴隨函數(shù)的形式，關(guān)于Sk(t)，Ck(t)，Bk(t)，Rk(t)，Dk(t)對哈密頓能量函數(shù)求偏導(dǎo)，并根據(jù)龐特里亞金極大值原理，證明目標(biāo)函數(shù)最小點(diǎn)處所有控制變量滿足如下要求：

通過求解上述方程，得到了在目標(biāo)函數(shù)約束下的最優(yōu)解，形式為：

因此，最優(yōu)控制變量的表達(dá)式等價于：

其中：k=1，2，…，n。最優(yōu)解可以實現(xiàn)每個狀態(tài)變量正定性的要求，最小化感染節(jié)點(diǎn)數(shù)和政府控制謠言的成本，為最佳管控點(diǎn)的確定提供了依據(jù)。

這些措施將耗費(fèi)大量人力、物力和財力，有必要求解管控用戶行為和投入宣傳的最佳水平。參考Lenhart提到的向前-向后四階Runge-Kutta 方法和最速下降法［24］，給定參數(shù)p=0.18，d=0.1，α=0.3，γ=0.5，λ=0.6，β=0.4，h=0.3，δ=0.01，ε=0.1，η=0.1。通過迭代得到最小化目標(biāo)函數(shù)J(u)和最優(yōu)控制解，如圖8（a）所示。當(dāng)?shù)?次迭代時，目標(biāo)函數(shù)達(dá)到了最優(yōu)值minJ(u)=15 580。之后，控制變量的顯著變化對目標(biāo)函數(shù)的影響并不明顯，因此，對應(yīng)的最優(yōu)控制解為

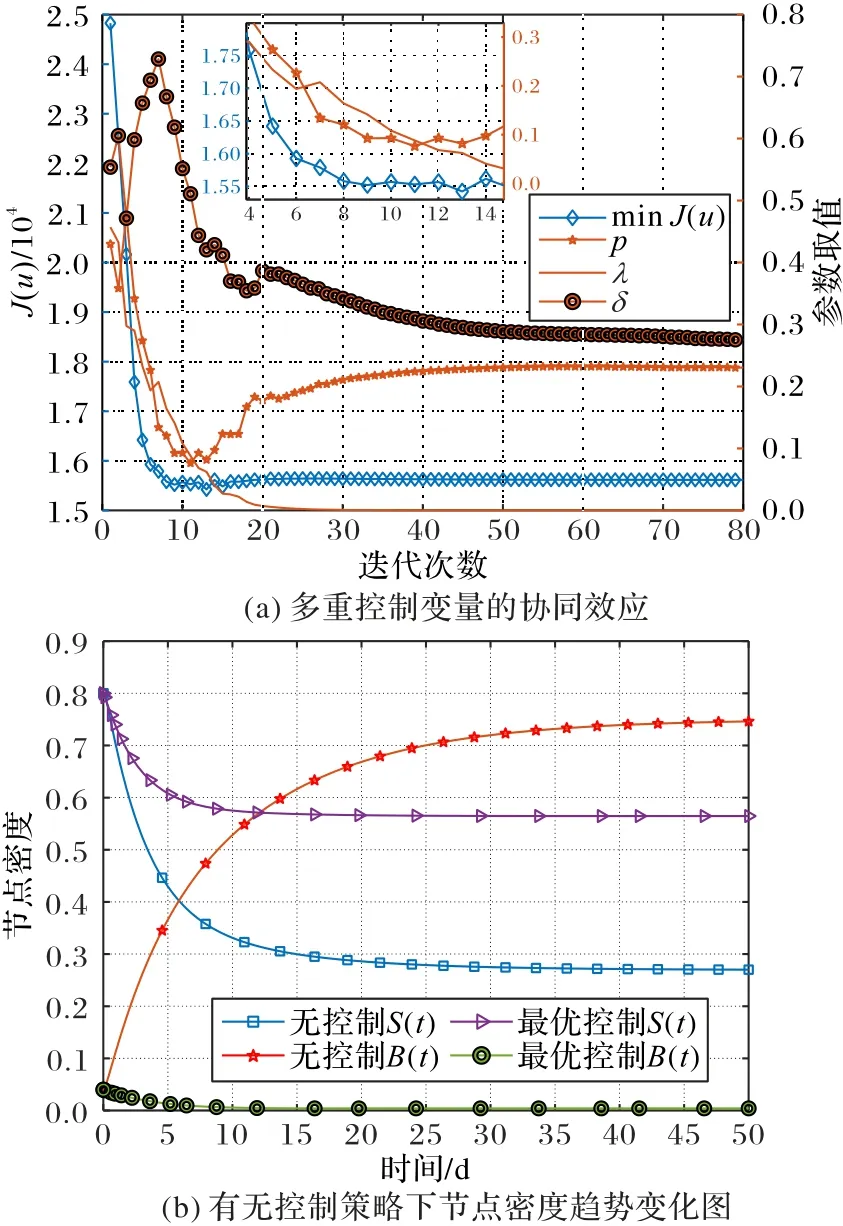
圖8 最優(yōu)控制的仿真分析圖Fig.8 Simulation analysis diagrams for optimal control

將有控制策略和未實施控制的情況進(jìn)行對比分析，通過調(diào)控用戶的轉(zhuǎn)發(fā)行為、加大政府辟謠的努力和媒體宣傳的力度，系統(tǒng)內(nèi)易感者數(shù)明顯上升，感染者數(shù)顯著下降且趨近于0，系統(tǒng)由流言平衡點(diǎn)變?yōu)闊o流言平衡點(diǎn)，謠言短期內(nèi)在小范圍擴(kuò)散且逐漸消失。這表明對系統(tǒng)實施等多重控制后抑制謠言擴(kuò)散的效果非常顯著。

4 實證分析

為了驗證模型在實際應(yīng)用中的可靠性，本章以新浪微博的實際數(shù)據(jù)為依托，利用Matlab 進(jìn)行擬合和參數(shù)估計。然后根據(jù)最小二乘法擬合的參數(shù)分析SCBRD 模型的演化趨勢，預(yù)測話題的發(fā)展情況。

4.1 數(shù)據(jù)采集

本節(jié)選擇了林生斌的相關(guān)話題，編寫了Python 代碼爬取數(shù)據(jù)，從應(yīng)用程序接口（Application Programming Interface，API）收集準(zhǔn)確的轉(zhuǎn)發(fā)、評論時間和文案。將開始時間設(shè)置為1，采樣頻率設(shè)置為1 d。爬取的時間段為2021 年8 月5 日到8 月24 日，以提取輿情信息在不同時間段的傳播特征。新浪微博的真實數(shù)據(jù)見表3。

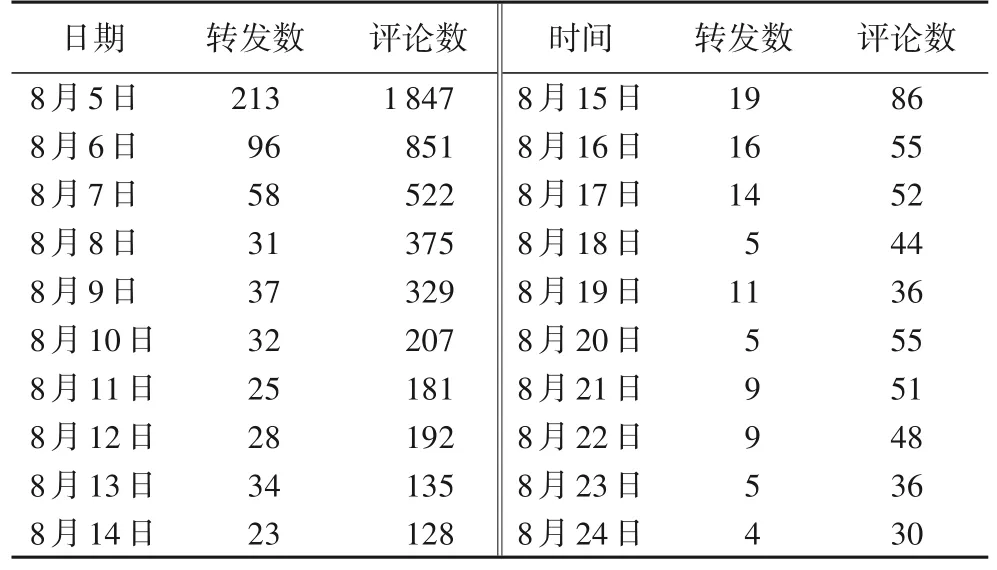
表3 2021年8月5日至8月24日的實際數(shù)據(jù)Tab.3 Actual data for August 5 to 24，2021

4.2 參數(shù)估計

為了有效模擬輿情傳播，選取了2021 年8 月5 日至8 月19 日的數(shù)據(jù)，利用最小二乘法進(jìn)行參數(shù)估計。不斷調(diào)整參數(shù)，從0.001 迭代到0.999，通過優(yōu)化函數(shù)即利用擬合誤差最小的思想估計模型SCBRD中的未知參數(shù)。結(jié)果如表4所示。

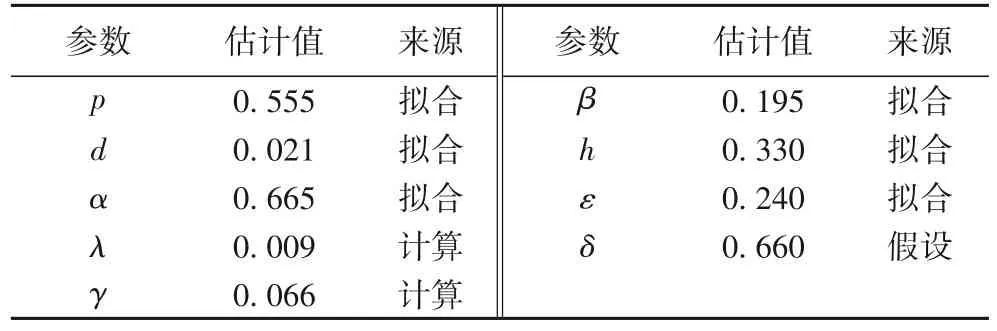
表4 未知參數(shù)的取值Tab.4 Values of unknown parameters

根據(jù)表4 的參數(shù)值可以求得R0大致為0.273 3，系統(tǒng)的閾值小于1。這表明截至2021 年8 月19 日，新浪微博上該輿論話題熱度會慢慢下降，公眾逐漸淡忘，不會形成大規(guī)模的輿論狂潮。同時，政府有必要采取措施鼓勵網(wǎng)民公眾，創(chuàng)造積極健康的網(wǎng)絡(luò)環(huán)境，減少公眾不恰當(dāng)?shù)囊庾R行為和盲目從眾帶來的不良后果。

接著，用最后5 d 的實際數(shù)據(jù)作為測試集以評估模型分析的準(zhǔn)確性。圖9 為基于真實傳播數(shù)據(jù)，SCBRD 模型在最優(yōu)擬合狀態(tài)下的B 態(tài)和C 態(tài)曲線。此時，轉(zhuǎn)發(fā)和評論兩組訓(xùn)練數(shù)據(jù)的擬合優(yōu)度分別為=0.947 1 和余弦相似度為cosθB=0.991 1，cosθC=0.990 8，說明該擬合程度非常好。進(jìn)一步計算了SCBRD 模型與測試數(shù)據(jù)集的均方根誤差（Root Mean Square Error，RMSE）為RMSEB=0.000 246，RMSEC=0.001 016，反映了本文SCBRD 模型在實際背景中的適用性。

圖9 數(shù)據(jù)擬合和預(yù)測結(jié)果Fig.9 Results of data fitting and prediction

由圖9 可知，在時間t=15 時，轉(zhuǎn)發(fā)人群趨于穩(wěn)定；且在t=25 時，評論人群也達(dá)到了穩(wěn)定狀態(tài)。那么，新浪微博上該話題將會得到控制，不再引起公眾的關(guān)注，與基本再生數(shù)的分析結(jié)果一致。因此，SCBRD 模型在演示輿情傳播規(guī)律方面是有效的，對現(xiàn)實中輿論話題的傳播速度、規(guī)模以及出現(xiàn)拐點(diǎn)的時間具有一定的指導(dǎo)意義。

4.3 模型比較

為避免偶然誤差，本文將SCBRD 模型分別與SCIR（Susceptible-inCubation-Infective-Refractory）模 型［25］、IDSRI（Ignorance-Discussant-Spreader-Remover-Ignorance）模 型［22］和SEIRD（Susceptible-Exposed-Infected-Recovered-Die hard infected）模型［26］進(jìn)行比較。對比實驗將擬合優(yōu)度R2和RMSE 作為評價指標(biāo)：R2越大，模型演化與預(yù)測數(shù)據(jù)的擬合越好；RMSE 越接近0，模型的預(yù)測效果越好。從表5 的實驗結(jié)果可見，SCBRD 模型的預(yù)測效果都優(yōu)于其他模型。例如，與SCIR 模型［25］相比，SCBRD 模型的擬合優(yōu)度提高了27.40%，且預(yù)測的均方根誤差減小了39.02%。這再次驗證了本文構(gòu)建的模型在輿情傳播指導(dǎo)方面的有效性。

表5 基于真實數(shù)據(jù)集的模型性能對比Tab.5 Performance comparison based on real datasets

5 結(jié)語

隨著在線社交網(wǎng)絡(luò)的日益流行，網(wǎng)民可以自由發(fā)表意見，充分體現(xiàn)了能動性和網(wǎng)絡(luò)的動態(tài)性。結(jié)合社交媒體的機(jī)制，本文構(gòu)建了一類考慮用戶能動性和流動性的SCBRD 輿情傳播模型。

首先，使用下一代矩陣方法計算了SCBRD 系統(tǒng)的閾值R0，并分析了其動力學(xué)特性。其次，利用數(shù)值仿真分析了反映用戶能動性和流動性的3 組參數(shù)對閾值R0的敏感性。結(jié)果表明：①三種意識行為中轉(zhuǎn)發(fā)行為表現(xiàn)得更為靈敏；主動防御行為一定程度上干預(yù)了信息的擴(kuò)散；而評論行為的效果最不明顯。②兩種心理反應(yīng)中，個體的好奇心理比群體產(chǎn)生的從眾效應(yīng)更突出，對輿情爆發(fā)的時間和規(guī)模更具影響力。③針對動態(tài)的社交網(wǎng)絡(luò)，控制系統(tǒng)的進(jìn)入率比減少離開率效果更好。然后，引入三重控制機(jī)制，利用龐特里亞金原理求得控制總成本最小條件下的最優(yōu)解。研究表明，當(dāng)最優(yōu)控制解為u*=(p*，λ*，δ*)=(0.120 3，0.164 1，0.667 6)時，效果最佳。最后，結(jié)合實際數(shù)據(jù)，計算出林生斌相關(guān)話題的基本再生數(shù)為0.273 3，說明該話題不會引發(fā)持續(xù)性討論狂潮，與實際是相符的。因此，該模型可以有效預(yù)測話題討論的規(guī)模和拐點(diǎn)出現(xiàn)的時間等，為輿情分析提供建議和指導(dǎo)。本模型也可用于口碑傳播、新產(chǎn)品的推廣等，有助于在線社交網(wǎng)絡(luò)開發(fā)新的商業(yè)模式。