反應譜法和時程分析法在高層抗震計算中的對比分析
王兆泉(濰坊瀚諾置業有限公司,山東 濰坊 262500)
結構力學理論的發展和建筑材料、施工設備的進步,使得人類可以修筑大量的高層、超高層建筑,這些建筑為大量人口集中、用地緊張的城市生活提供了居住和商業空間,使得單位面積的城區可以承載更多的城市人口[1]。高層建筑在垂直方向上的發展面臨著諸多挑戰,其中結構抗震問題成為最為重要的一項。這是因為高層建筑積累了大量的城市財富,也是人類密集活動的場所,由于地震是一個復雜且難以預測的自然災害,在地震發生時如果高層建筑的抗震設計不足,往往導致災難性的后果[2]。因此,高層建筑抗震設計成為目前工程領域的研究熱點之一[3-5]。
本文結合實際工程項目案例,以反應譜法和時程分析法分別計算了高層建筑在地震作用下的剪力響應特征,研究2 種抗震設計方法的不同,研究成果可為目前大量的高層建筑、超高層建筑抗震設計提供有益參考,為抗震設計方法的選擇和地震波的確定提供借鑒。
1 工程概況
山東省濰坊市某超高層建筑為集商業、住宅為一體的多功能綜合體建筑,建筑由1棟塔樓和底部裙樓組成,塔樓高度為58 層,主要用于商業辦公和住宅,底部3層裙樓為商業樓,設置2層地下室。塔樓為現澆混凝土框架剪力墻結構,部分剪力墻直接在首層通過梁式轉換結構支承在框架支柱上,塔樓總高度為185m,平面長度為29m,平面寬度為26m,設計使用年限為50年,建筑結構安全等級為二級,抗震設防烈度為7 度,地震加速度0.15g,建筑抗震設防類別為丙類,阻尼比為0.05,場地類別為II 類,采用樁基礎,樁基直徑為600mm,樁長為25m,樁間距為5m,場區巖土工程地質條件如表1所示。
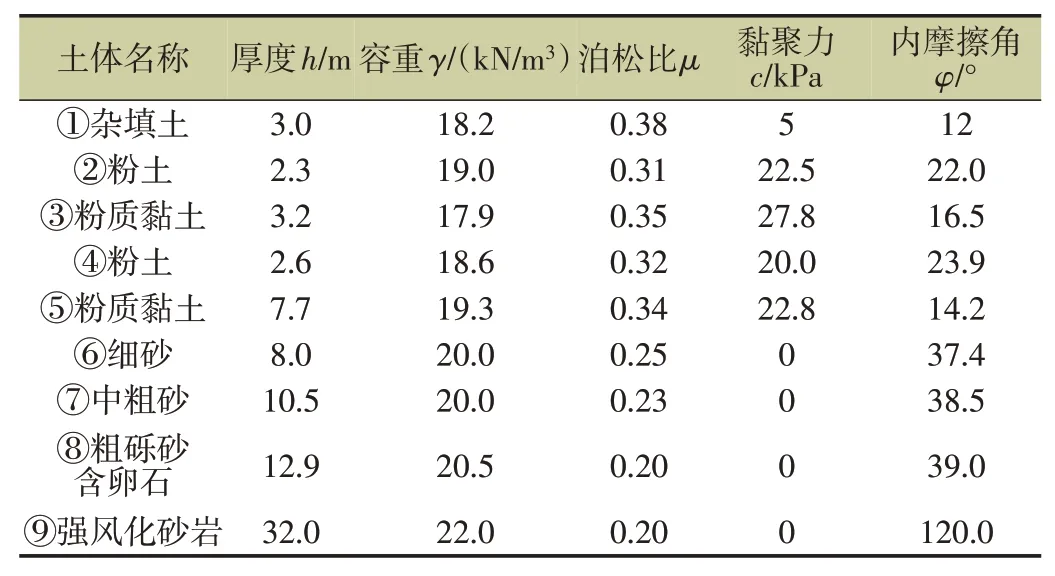
表1 場區巖土體物理力學參數
超高層建筑上部結構的墻體、梁體和柱體的幾何尺寸和混凝土等級信息如表2 所示。結構板厚均為120mm,樓頂屋面厚度為140mm,標準層樓面恒載為3kN/m2,活荷載為2kN/m2。
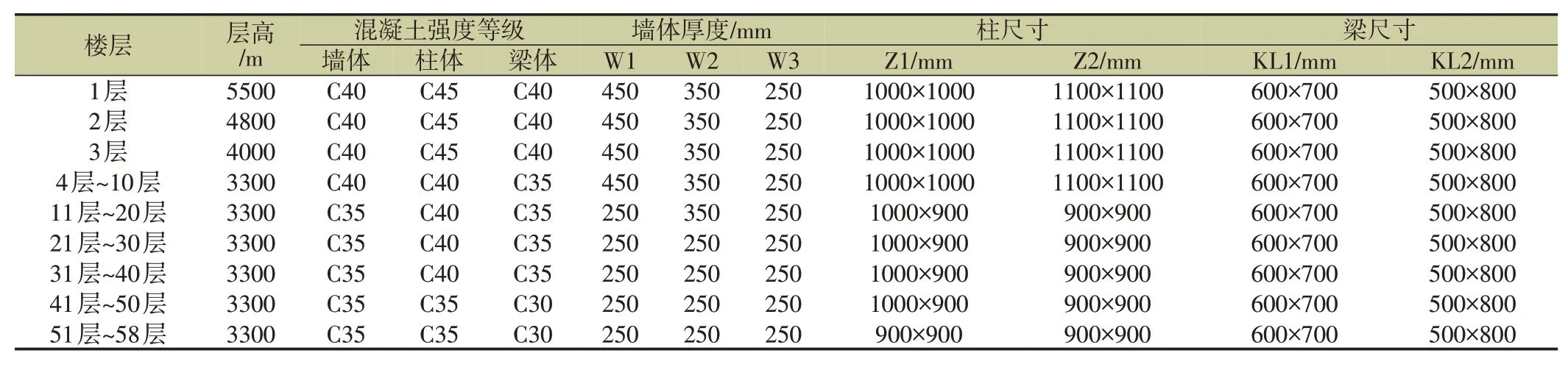
表2 建筑墻體、梁體和柱體的幾何尺寸和混凝土等級
2 反應譜法和時程分析法基本計算原理
2.1 反應譜法的基本計算原理
反應譜法和時程分析法均是評估高層建筑在地震作用下的響應分析方法。反應譜法是一種基于單質點體系運動特性的計算方法,單支點體系在地面運動作用下的運動方程如公式(1)所示,該方法具有清晰、計算簡單的特點。反應譜法是我國目前地震抗震計算中的基本計算方法,利用了振型分解和正交性原理,在給定的地震加速度記錄中,將復雜的結構振動問題分解為多個獨立的振型問題,化時變動力問題為擬靜力問題,只取少數幾個低階振型求解不同振型作用下結構的最大位移、最大振動速度和加速度反應,就能反應結構最大彈性地震反應,進而驗證結構構件的抗震承載力和變形驗算[6]。
式中m為單質點的質量,kg;x?為質點在地震作用下的相對加速度,m/s2;x?為質點在地震作用下的相對速度,m/s;x 為質點在地震作用下的相對位移,m;k為質點剛度,kN/m;c為阻尼。
公式(1)可以運用單子點體系的振動理論和Duhamel積分進行求解,如公式(2)所示。
式中ξ為阻尼比;w為振動頻率,Hz。
2.2 時程分析法的基本計算原理
與反應譜法不同,時程分析法是隨著強地震記錄增多和計算機硬件設備發展的基礎上興起的精細計算方法[7-8]。該方法是一種直接求解結構物運動微分方程的方法,在數學上稱之為步步積分法,考慮了結構非線性行為、場地效應和復雜的地震動特性,求解整個時間歷程內地震作用效應的一種結構動力計算方法,該方法是比底部剪力法和振型分解反應譜法更為可靠和合理。時程分析法通過輸入與結構所在場地相對應的地震波作為地震荷載,由初始狀態(靜止狀態)開始,對結構的基本運動微分方程進行逐步積分求解,直至地震作用終止,能夠較為精確地確定結構在地震荷載作用下的內力與變形隨時間變化的全過程,并發現結構在地震時可能存在的薄弱環節和可能發生的震害[9]。規范中特別規定對于特別不規則的建筑、甲類建筑以及超過一定高度的高層建筑,宜采用時程分析法作為補充計算,高層建筑在地震作用下的運動方程如公式(3)所示,式中各符號的含義與公式(1)一致,只不過公式(3)的各參數均為矩陣。
將地震作用時間劃分為許多微小的時段,相隔△t,基本運動方程可以改寫為i時刻至i+1時刻半增量微分方程,如公式(4)~公式(5)所示。
時域分析不需要進行模態分析也能進行,以上公式需要借助計算機程序進行求解,通過把時間離散為一個個時間段,如0.02s,然后每個時間更新結構的動力荷載及動力剛度,通過每一步的靜力求解得到下一步的響應,所以叫作逐步積分法,上一步的計算結果影響下一步的計算結果。
3 地震波加速度曲線的選取
為了比較時程分析法與反應譜法在高層建筑抗震計算中的不同,合適的地震波加速度顯得尤為重要。地震波加速度曲線包含了地震動的持續時間、頻譜范圍、持續時間等地震動參數,考慮結構在地震烈度為7度時的場地條件,研究選取2條不同頻譜特征的地震波進行計算,分別為天然Hector Mine地震波和天然Imperial地震波,地震波的時程曲線圖譜如圖1、圖2所示。
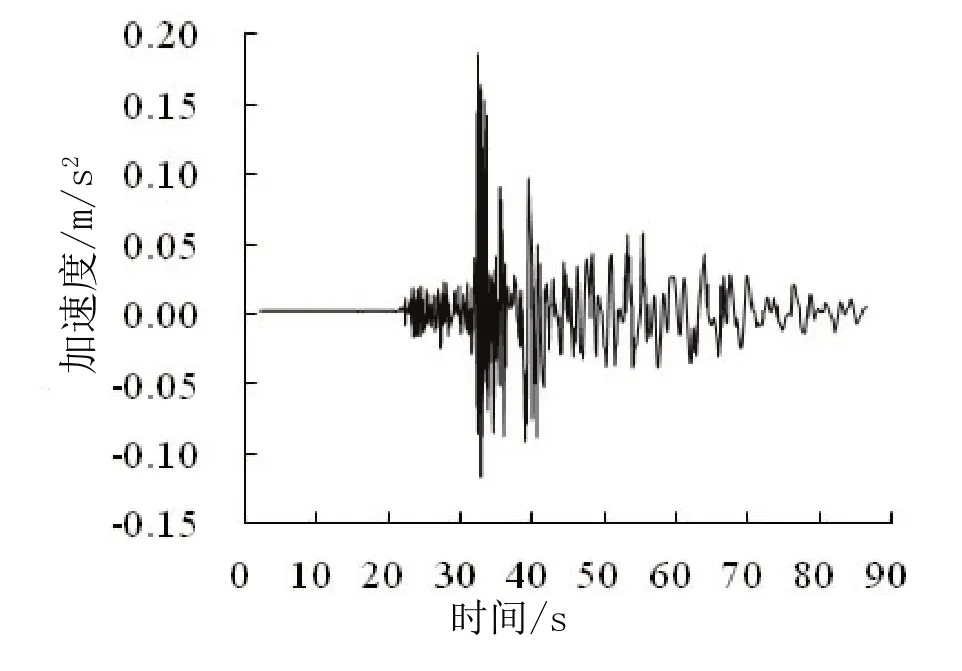
圖1 天然Hector Mine地震波加速度時程曲線
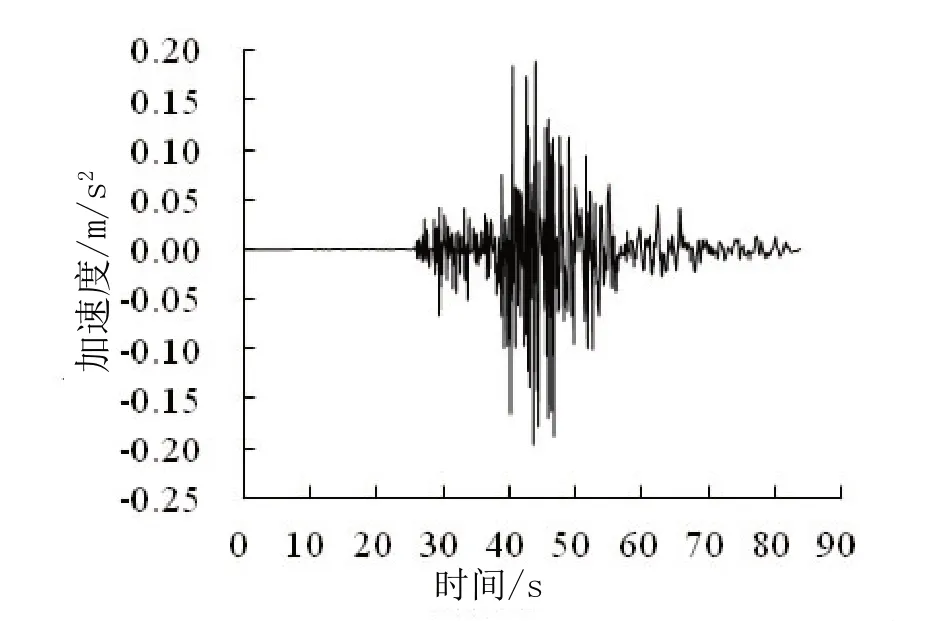
圖2 天然Imperial地震波加速度時程曲線
4 反應譜法和時程分析法在高層抗震計算中的對比分析
計算采用美國CSI 公司的ETABS9.2.0 中文版軟件進行計算,計算時中梁剛度增大系數取1.5,梁端彎矩調幅系數為0.7,梁設計彎矩增大系數為1.0,連梁剛度折減系數為0.5,梁扭矩折減系數為0.4,混凝土容重取為25kN/m2,鋼筋鋼材為Q235鋼,鋼容重為78kN/m2,墻體水平分布筋類別為HPB235,墻體豎向筋類別為HRB335,墻體水平分布筋間距為200mm,墻體豎向分布筋配筋率為0.3%,梁箍筋和柱箍筋類別為HPB300。不同地震荷載作用下,反應譜法和時程分析法計算得到高層建筑的X向樓層剪力如圖3所示,Y向樓層剪力如圖4所示。

圖3 不同天然地震波條件下時程分析法和反應譜法X向樓層剪力對比
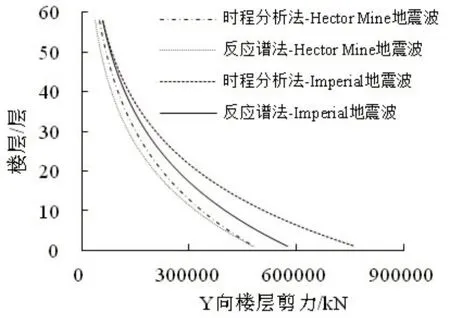
圖4 不同天然地震波條件下時程分析法和反應譜法Y向樓層剪力對比
從圖3 中可以看出,在不同天然地震波條件下,時程分析法和反應譜法對樓層剪切力的分布規律不產生明顯影響,隨著樓層的增加,X 向樓層剪力呈現指數降低的趨勢,建筑物底層的剪力最大,變化范圍在600000kN~900000kN;天然Hector Mine 地震波和天然Imperial 地震波作用時,采用時程分析法得到的X 向樓層剪應力值相近,以底層剪力為例,天然Hector Mine地震波作用下的X向樓層剪力為764798kN,天然Imperial地震波作用的X向樓層剪力為7609846;而采用反應譜法計算時,天然Hector Mine 地震波作用下的X 向樓層剪力明顯大于天然Imperial 地震波作用的X 向樓層剪力,以底層剪力為例,天然Hector Mine地震波作用下的X向樓層剪力為860398kN,天然Imperial地震波作用的X向樓層剪力為672553kN。
從圖4 中可以看出,在不同天然地震波條件下,時程分析法和反應譜法對樓層剪切力的分布規律不產生明顯影響,隨著樓層的增加,Y 向樓層剪力呈現指數降低的趨勢,建筑物底層的剪力最大,變化范圍在500000kN~800000kN,比X 向樓層剪力小;天然Hector Mine地震波和天然Imperial地震波作用時,采用時程分析法和反應譜法計算得到結果均為天然Hector Mine地震波作用下的Y 向樓層剪力明顯小于天然Imperial 地震波作用的Y向樓層剪力,以底層剪力為例,天然Hector Mine地震波作用下時程分析法計算的Y向樓層剪力為480394kN,天然Imperial 地震波作用下時程分析法計算的Y 向樓層剪力為764798kN;天然Hector Mine 地震波作用下反應譜法計算的Y 向樓層剪力為477999kN,天然Imperial地震波作用下反應譜法計算的Y向樓層剪力為576473.6635kN。
5 結語
以山東省濰坊市某超高層商住一體建筑為研究對象,選取2 個不同的天然地震波,運用反應譜法和時程分析法分別計算結構的樓層剪力,得到以下幾個結論:
(1)在不同天然地震波條件下,時程分析法和反應譜法對樓層剪切力的分布規律不產生明顯影響,隨著樓層的增加,X向和Y向樓層剪力均呈現指數降低的趨勢,建筑物底層的剪力最大。
(2)天然Hector Mine地震波和天然Imperial地震波作用時,采用時程分析法得到的X 向樓層剪應力值相近,采用反應譜法計算時,天然Hector Mine地震波作用下的X 向樓層剪力明顯大于天然Imperial 地震波作用的X向樓層剪力。
(3)天然Hector Mine地震波和天然Imperial地震波作用時,采用時程分析法和反應譜法計算得到結果均為天然Hector Mine地震波作用下的Y向樓層剪力明顯小于天然Imperial地震波作用的Y向樓層剪力。

