基于改進模擬退火算法的工業機器人絕對定位精度提高

黃?智，閔?杰, 2，陳貴科，饒志敏，辛?強，趙?尋

基于改進模擬退火算法的工業機器人絕對定位精度提高

黃?智1，閔?杰1, 2，陳貴科1，饒志敏3，辛?強3，趙?尋3

(1. 電子科技大學機械與電氣工程學院，成都 611731；2. 中國船舶集團有限公司第七一○研究所，宜昌 443003；3. 中國科學院光電技術研究所，成都 610207)

工業機器人在拋光大口徑光學元件時由于其較低的絕對定位精度，使得加工元件較難達到較高的面形精度．本文提出一種通過考慮測量坐標系與機器人基坐標系之間的轉換誤差、機器人的運動學誤差以及機器人法蘭端到工具坐標系的測量誤差等多誤差源構建工業機器人綜合誤差模型的校準方法．通過仿真實驗與PSO、AFSA、SA算法進行對比，證明改進后的Be-SA算法在辨識誤差參數時具有更快的收斂速度和更高的精度．實驗結果表明通過Be-SA算法辨識后的KUKA KR 120 R3900的平均絕對定位誤差由2.497mm降低為0.321mm，最大絕對定位精度由3.358mm降低為0.961mm，構建的綜合誤差模型在辨識運動學誤差參數時具有良好的適用性，改進后的Be-SA算法能有效提高機器人的絕對定位精度，對于磨拋大口徑光學元件的性能提升具有重要參考價值．

工業機器人；絕對定位精度；模擬退火算法；誤差模型

因此本文充分考慮上述誤差因素，通過分析測量坐標系與機器人基坐標系之間的轉換誤差、機器人的運動學誤差以及機器人法蘭端到工具坐標系的測量誤差，基于工業機器人的DH模型構建誤差模型．通過基于SA算法改進后的Be-SA算法對誤差參數進行辨識，并通過仿真實驗與傳統PSO、AFSA、SA算法進行對比，證明改進后的Be-SA算法在辨識誤差參數時具有更快的收斂速度和更高的精度．最后進行實驗驗證，Be-SA算法對提升機器人的絕對定位精度具有較好的效果．

1?誤差模型與辨識方法的數學模型

1.1?誤差模型的建立

工業機器人的運動學模型以1955年Danevit和Hartenberg提出的DH模型[11]的使用最為廣泛，該模型以連桿長度、連桿扭角、關節變量和關節偏置作為辨識參數，將每個關節的坐標系通過一定規則固定在連桿上，各個坐標系之間通過其次變換矩陣進行坐標轉換，即

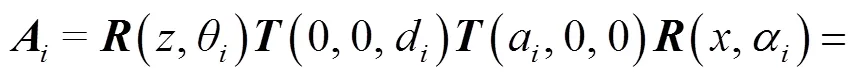
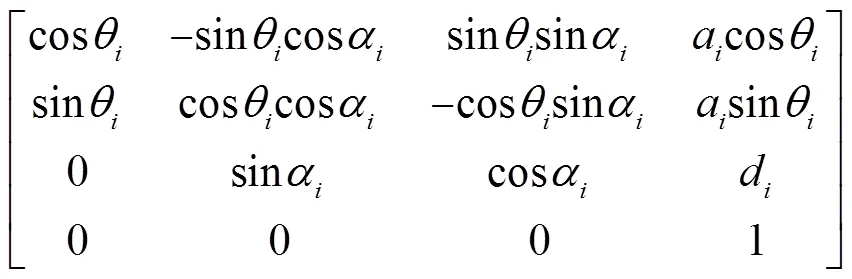
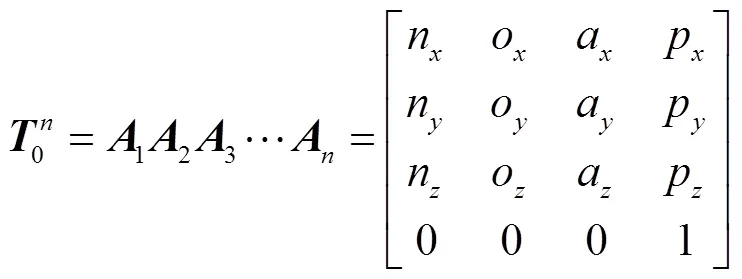
而測量坐標系到機器人的基坐標系轉換矩陣為

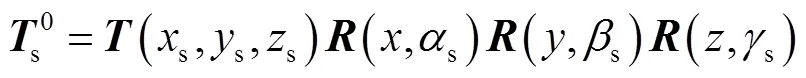
機器人的法蘭端到工具坐標系的轉換中不用考慮其位姿變化，則轉換矩陣為

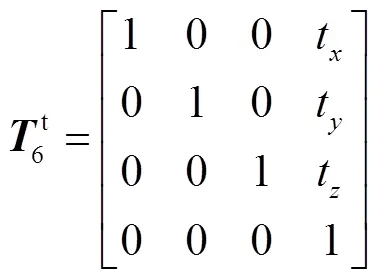
則名義上激光跟蹤儀測得的靶球的位置為

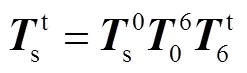
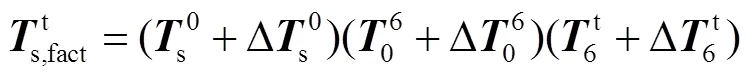
則實際位置與名義位置的誤差為

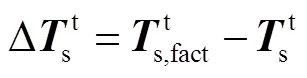
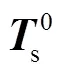
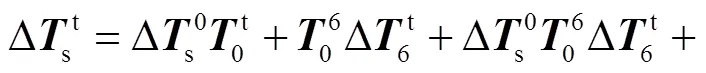
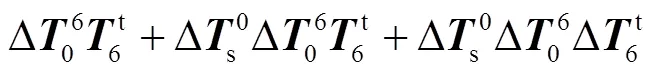
其中

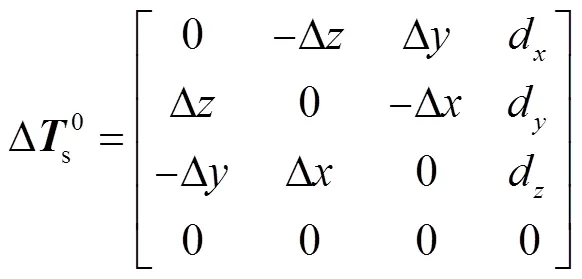
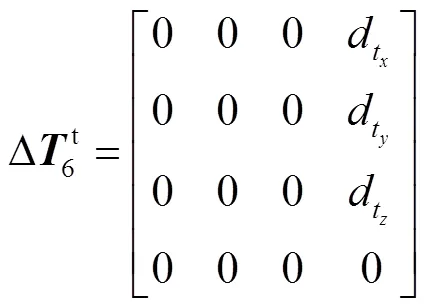
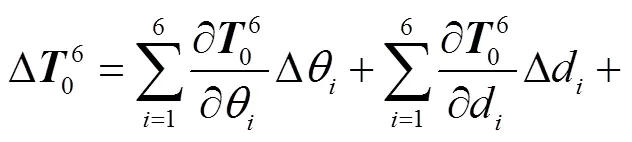
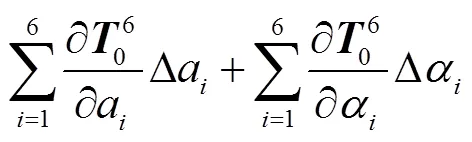
舍棄掉高階無窮小分量則有

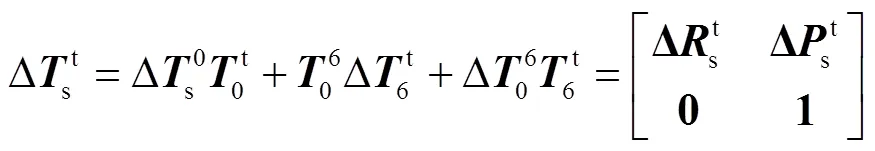
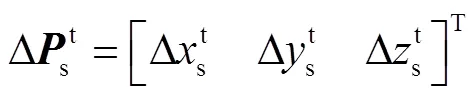
1.2?目標函數的建立

由于以提高絕對定位位置精度為目的，因此忽略位姿誤差，于是目標函數采用平均絕對定位精度作為指標，即

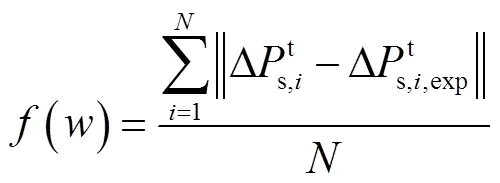
1.3?Be-SA算法

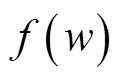
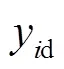
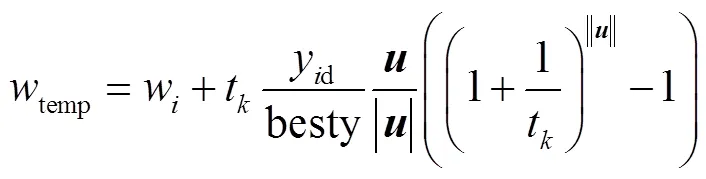
步驟4進行判斷．

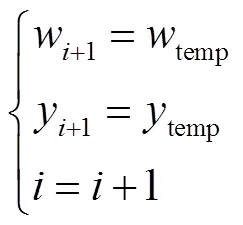
否則不接受該解，繼續進行迭代．

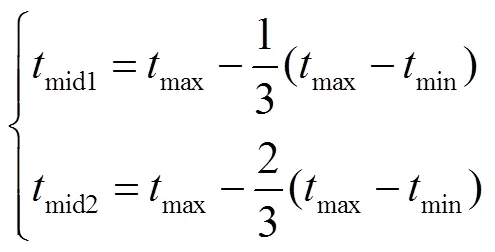
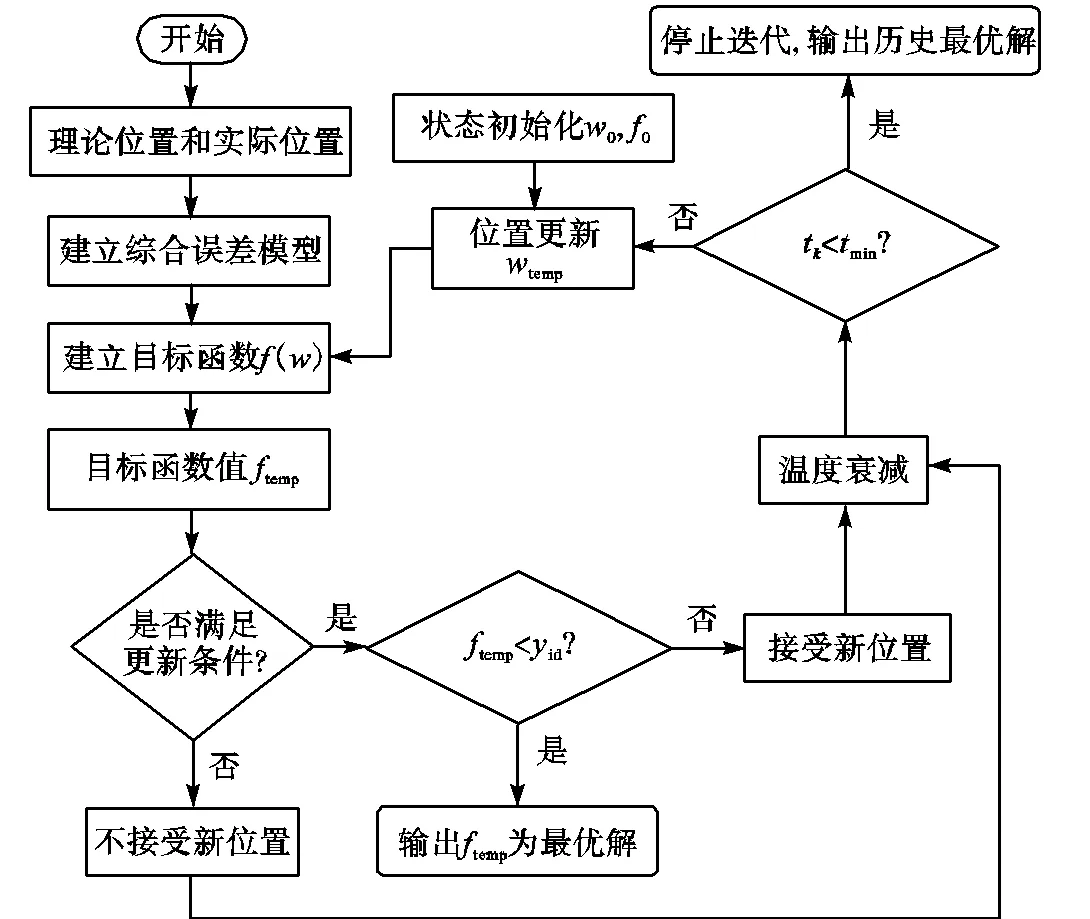
圖1?算法優化流程

隨著溫區的變化，為避免在低溫區跳過關鍵位置，衰減率逐漸降低，則溫度的更新如下：

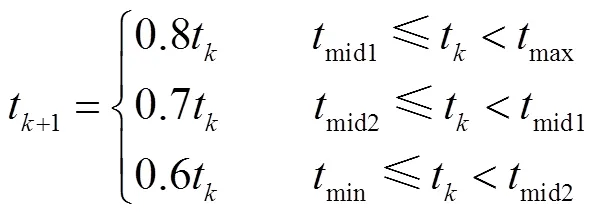
2?仿真驗證

為確保改進后的Be-SA算法確實能有更快的收斂速度和更高的尋優精度，故通過設計該仿真實驗來進行驗證，同時與文獻[17]中提到的SA算法、粒子群優化(particle swarm optimization，PSO)算法和人工魚群算法(artificial fish school algorithm，AFSA)進行對比，后文中算法表達均用字母進行表示．

2.1?仿真數據設置

采用KUKA KR 120 R3900機器人進行仿真，仿真驗證流程如圖2所示，其DH運動學參數見表1.參考他人辨識結果大小范圍[18]，在該范圍內隨機生成這33個誤差參數，在這些預設的誤差參數作用下產生位置誤差，將其用于智能算法辨識，最后根據辨識求解得到的誤差參數產生的位置誤差，與預設的這些誤差參數產生的位置誤差進行作差對比，根據作差結果越小就表明辨識的越準確，從而用于評價智能算法的有效性．預設的運動學誤差參數如表2所示，測量坐標系到基坐標系、法蘭坐標系到工具坐標系的誤差參數預設如表3所示．

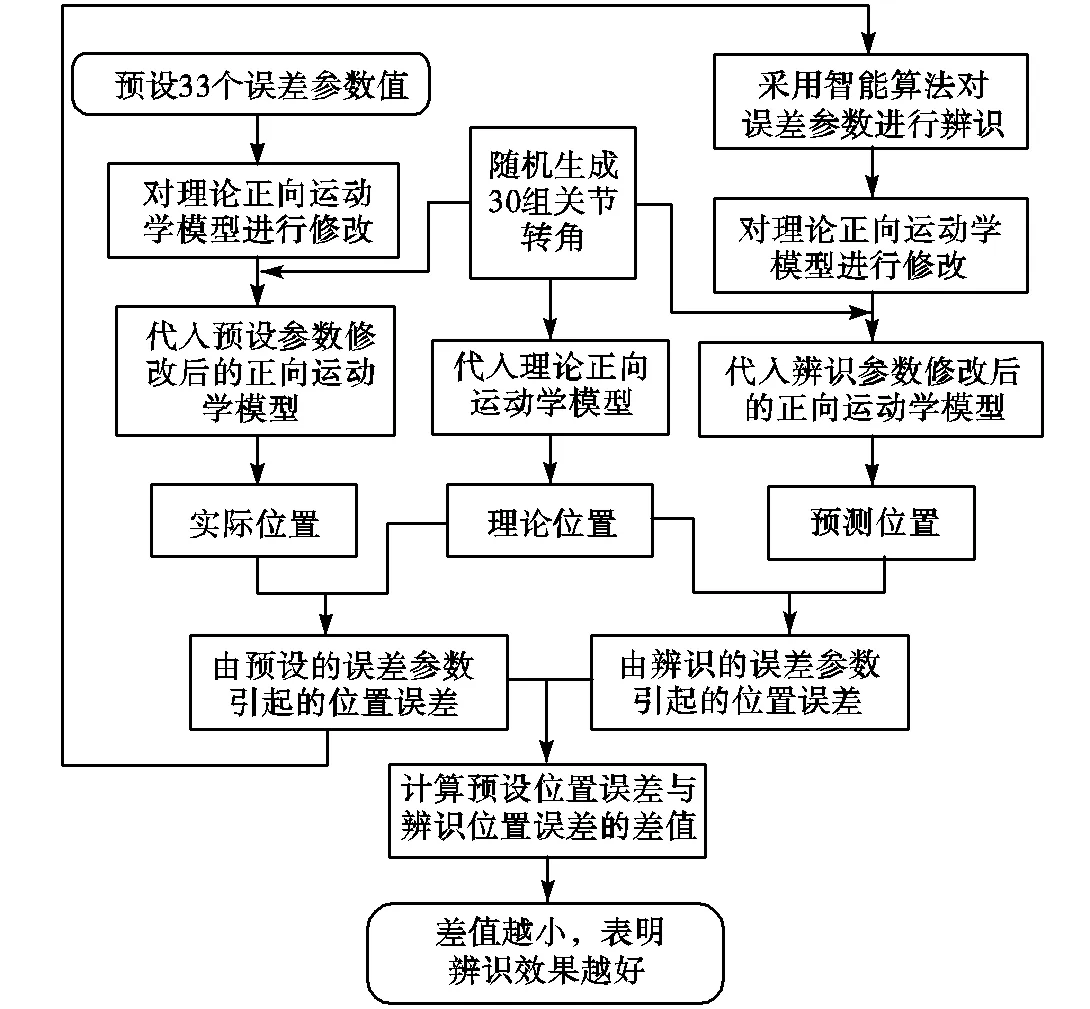
圖2?仿真驗證流程

表1 KUKAKR 120 R3900機器人DH運動學模型參數

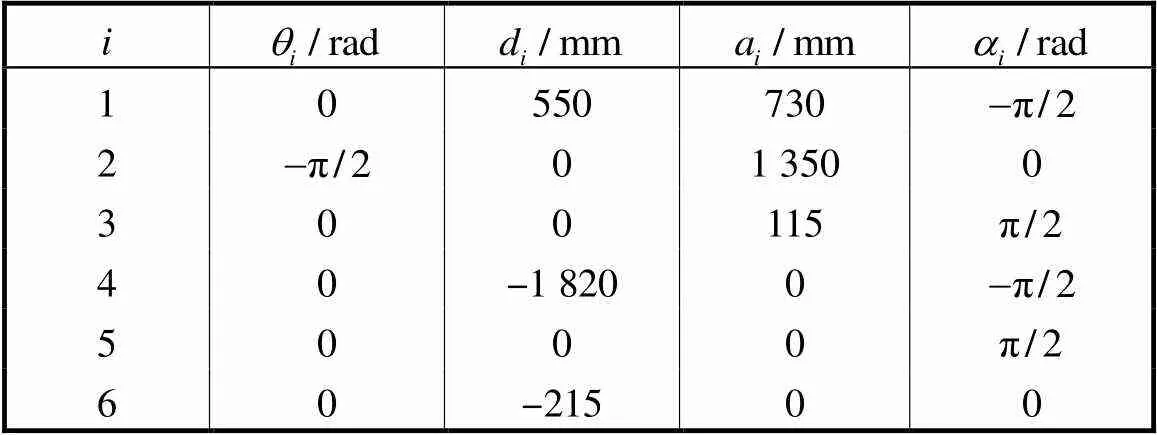
Tab.1 Nominal parameters of the DH kinematics model of the KUKA KR 120 R3900 robot

表2?KUKAKR 120 R3900機器人運動學誤差參數

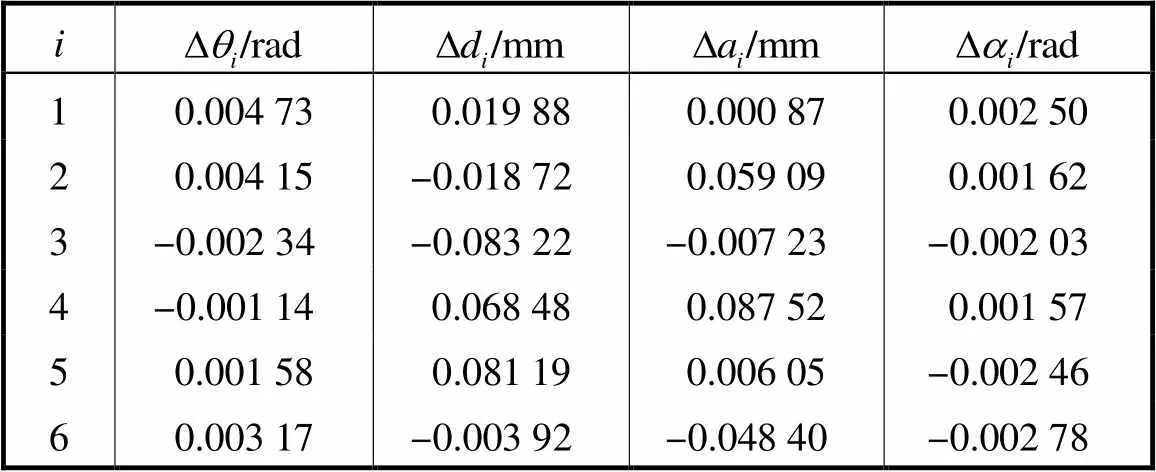
Tab.2 Kinematics error parameters of the KUKA KR 120 R3900 robot

表3?各坐標系轉換誤差參數

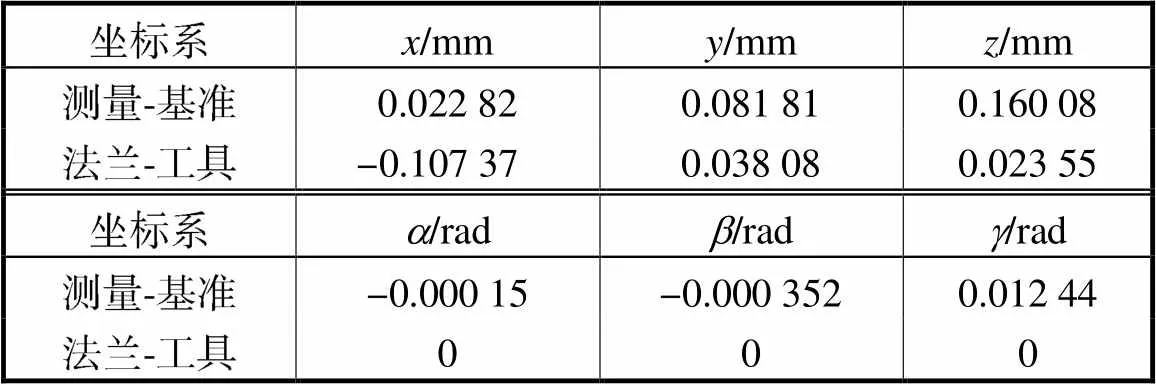
Tab.3 Conversion error parameters of each coordinate system

只考慮位置誤差，設置目標函數為

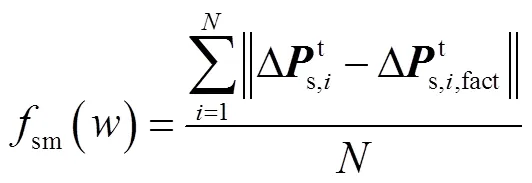
2.2?仿真結果與討論

分別采用改進后的Be-SA、SA、PSO、AFSA算法以式(20)為目標函數進行尋優，其目標函數值收斂如圖3所示，30組位置誤差對比如圖4所示．由于算法初始值均隨機生成，則各個算法的初始點均有所不同．

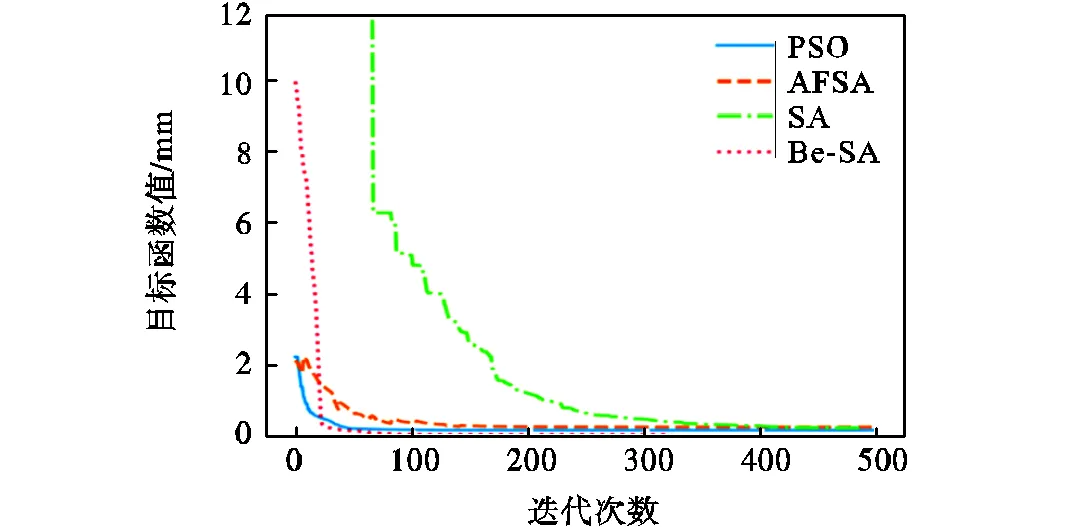
圖3?不同優化算法目標函數值收斂

圖3可以看出Be-SA算法具有最快的收斂速度，PSO算法相較于SA算法和AFSA算法具有較快的收斂速度，同時SA算法能有效跳過局部最優，但收斂最慢，而AFSA易陷入局部最優．從圖4和表4可以看出Be-SA算法相較于其他3種算法具有最高的預測精度，且數據整體波動較小，能有效避免某點位置誤差較大的情況出現．

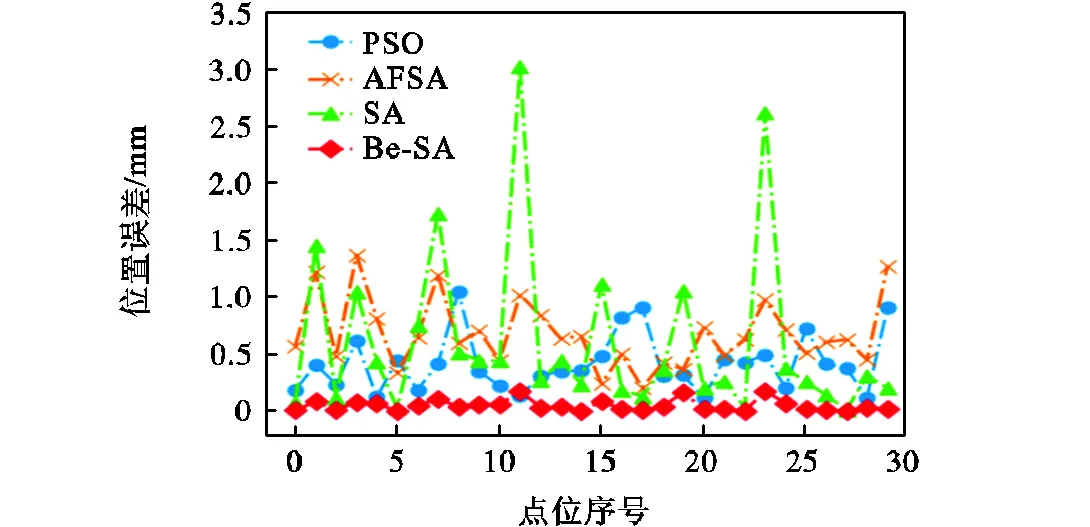
圖4?不同優化算法位置誤差對比

表4?不同優化算法的仿真結果對比

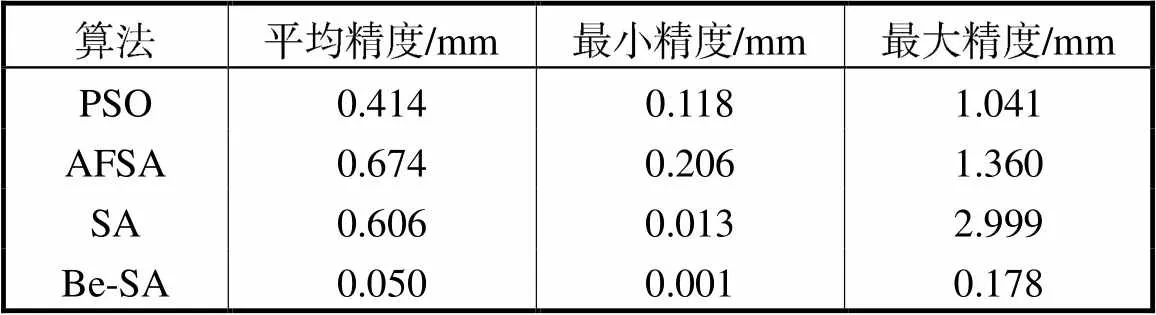
Tab.4 Comparison of the simulation results of different optimization algorithms

因此相較于SA算法的完全隨機方向尋優，由于本文通過改進搜索步長和對衰減率在不同溫區的表現優化，改進后的Be-SA算法在工業機器人的運動學誤差參數的辨識上具有更快的收斂速度和更高的尋優精度．

3?誤差參數辨識實驗

圖5為離線誤差補償流程，圖6為工業機器人的實驗現場，采用的機器人為KUKA KR 120 R3900，靶球通過磁鐵吸附的方式安裝在工具末端，采用激光跟蹤儀測量靶球位置，并導入進測量計算機中．靶球相對于機器人法蘭端的位置已測量好存入示教器中．

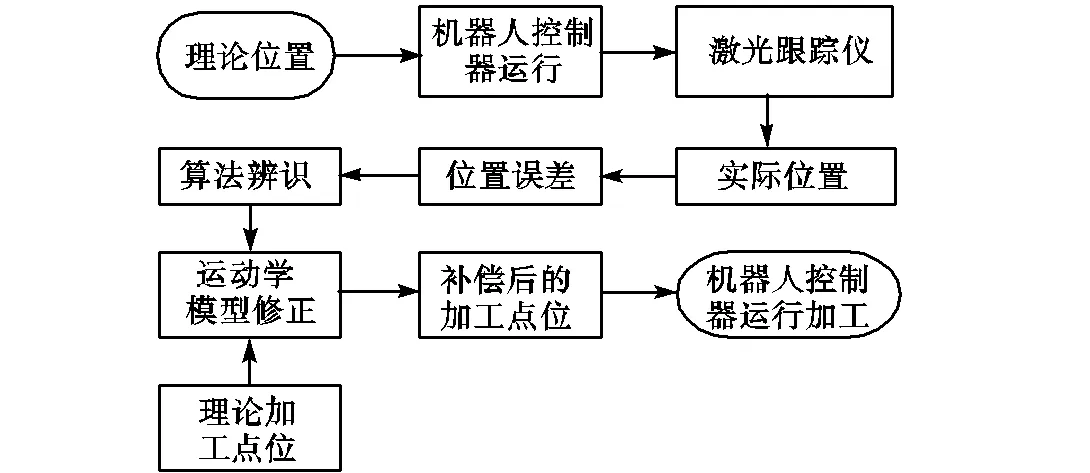
圖5?誤差補償流程

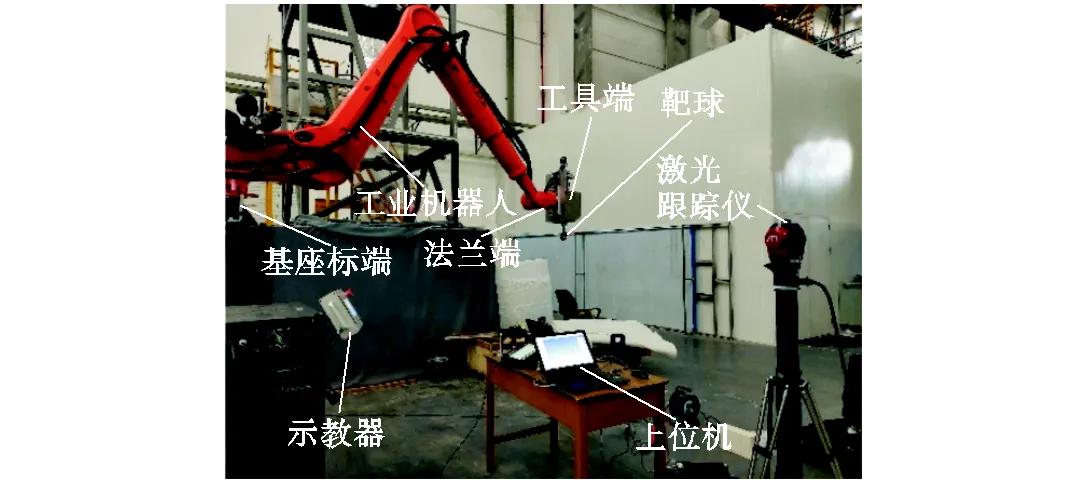
圖6?實驗現場

3.1?基于Be-SA的誤差參數辨識

由于在第2節的仿真實驗中證明了Be-SA算法具有更快的收斂速度和更高的尋優精度，于是采用該算法對實驗結果進行處理．首先采用蒙特卡洛方法生成機器人的工作空間，KUKA KR 120 R3900的工作空間如圖7所示，使用隨機選取的方法在工作空間內隨機選取100個點，通過示教器控制點位移動到隨機選取點，并采用激光跟蹤儀進行測量得到其誤差．對于選取的100個點誤差，采用式(14)作為目標函數通過Be-SA算法進行迭代尋優，其目標函數值收斂如圖8所示，最終求得目標函數全局最優解為0.254mm．

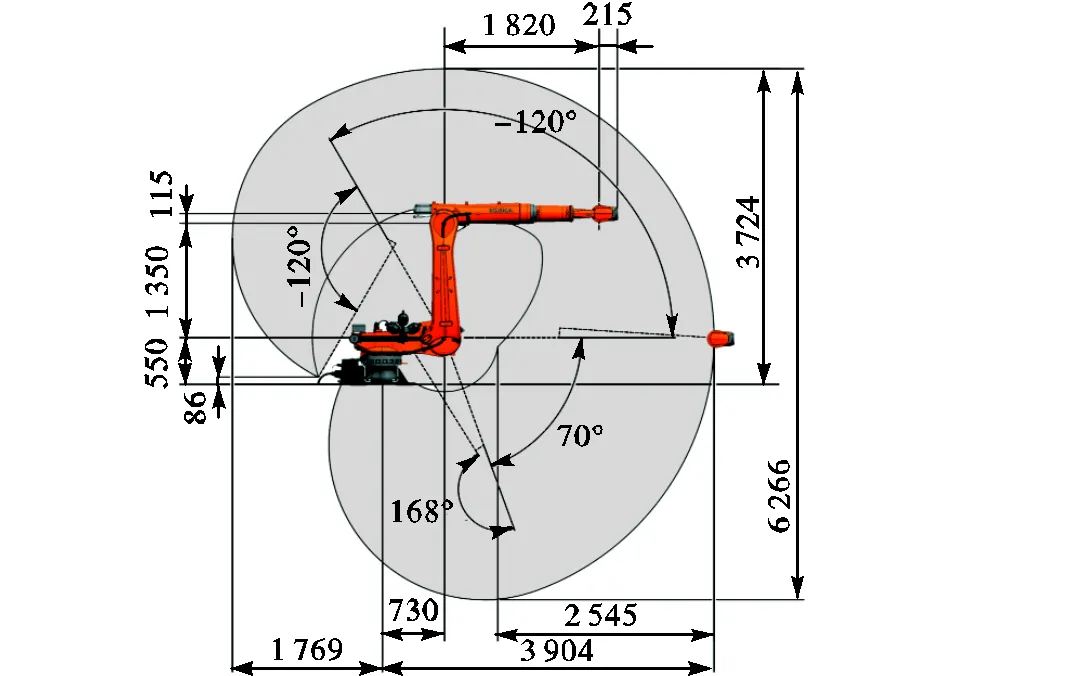
圖7?KUKA KR 120 R3900的工作空間(單位：mm)

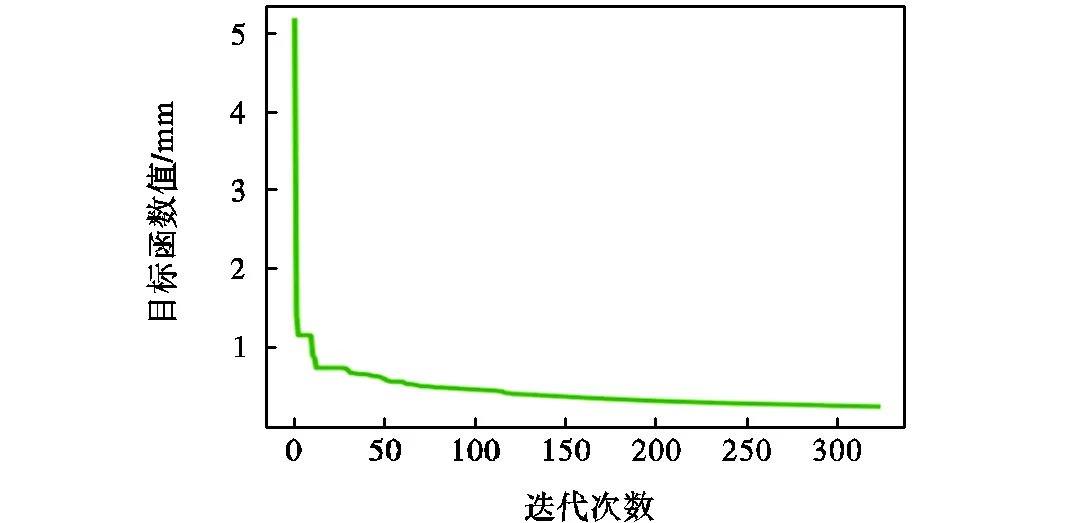
圖8?目標函數值收斂

3.2?分析與討論

通過采用圖9的空間立方體布點方式來對第3.1節求得的最優解進行驗證．通過Be-SA算法辨識后的誤差參數，將這些誤差參數對原來的機器人參數進行標定，將標定后的結果與實驗測量結果進行對比，其誤差參數標定前后結果對比如表5所示，位置誤差對比如圖10所示．

圖9?驗證點的選取

表5?誤差參數標定前后結果對比

Tab.5 Comparison of results before and after error pa-rameter correction

從圖10可以看出，標定后的位置誤差曲線波動較小，證明Be-SA算法辨識得到的誤差參數具有很好的適用性，能很好地普遍應用于機器人絕對定位精度提升中．從表5可以看出，經過標定后機器人絕對定位平均精度從2.497mm提升至0.321mm，最大誤差從3.358mm降低至0.961mm，證明Be-SA算法對于機器人的絕對定位精度的提升有著良好的作用．同時由于充分考慮了測量坐標系與機器人基坐標系和機器人法蘭坐標系與工具坐標系之間的測量誤差，使得誤差來源的辨識更加詳細，因此具有很好的廣泛應用性，以及擁有更高的絕對定位精度．

但在實際過程中，由于機械臂的自重、溫度、齒輪間隙等一系列非運動學的影響，會同樣對機器人末端造成誤差，并且這些誤差因素無法通過辨識運動學參數的方法辨識出來．但仍有跡可循，從圖9可以看出，試驗點是按照立方體一個一個選取，而觀察圖10標定前的曲線和標定后的曲線，其誤差分布按照每隔幾點重復相同誤差的規律變換．因此可以表明，隨著選取測量點網格的變化，位置誤差也在隨之有規律地變化，這為接下來非運動學誤差的辨識研究提供了方向．

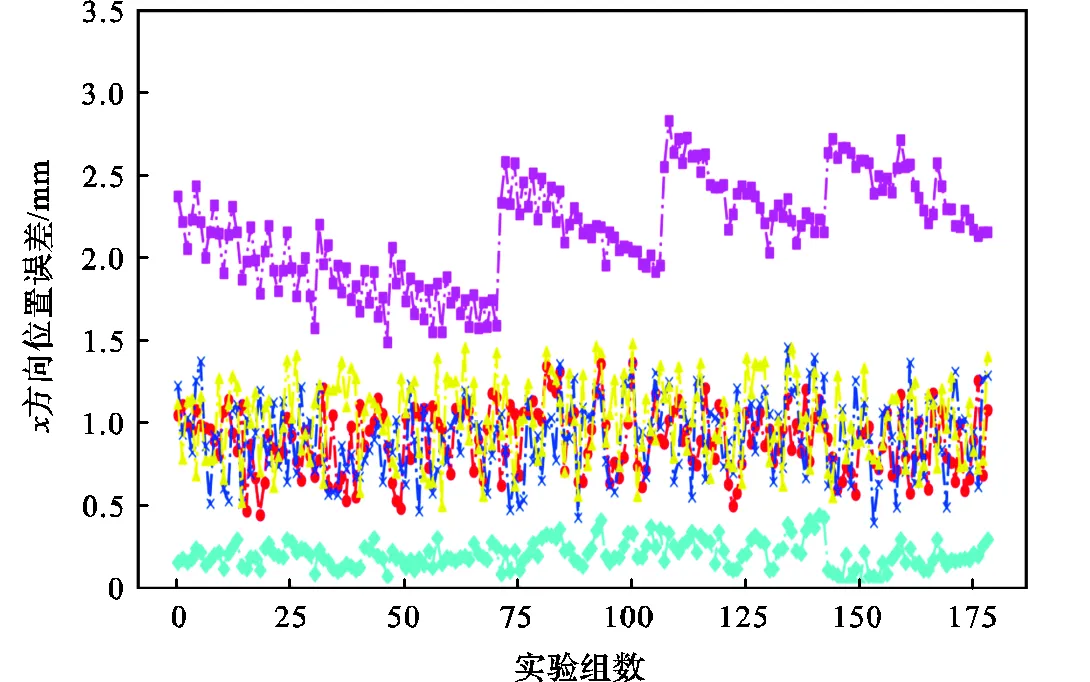
（a）方向位置誤差標定前后對比

（b）方向位置誤差標定前后對比

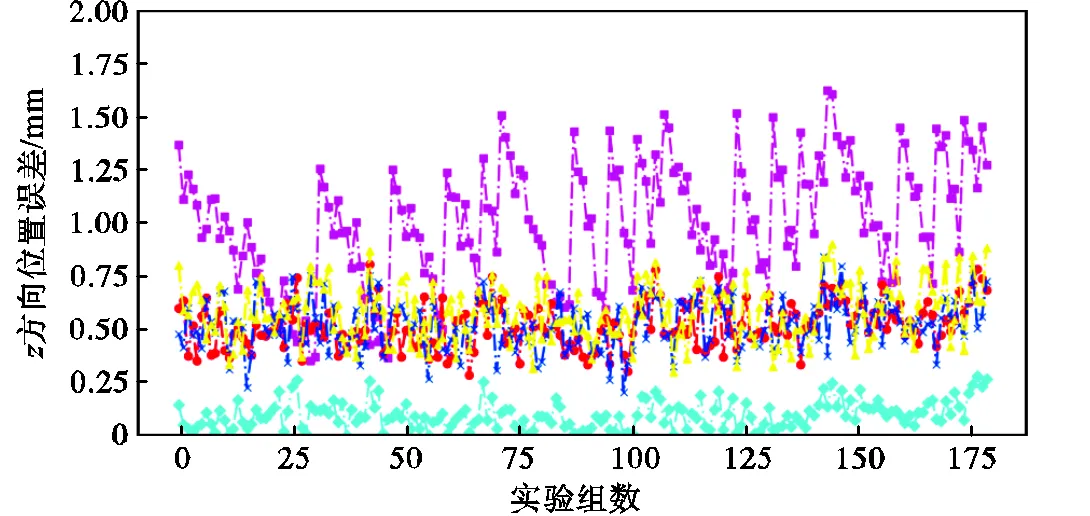
（c）方向位置誤差標定前后對比

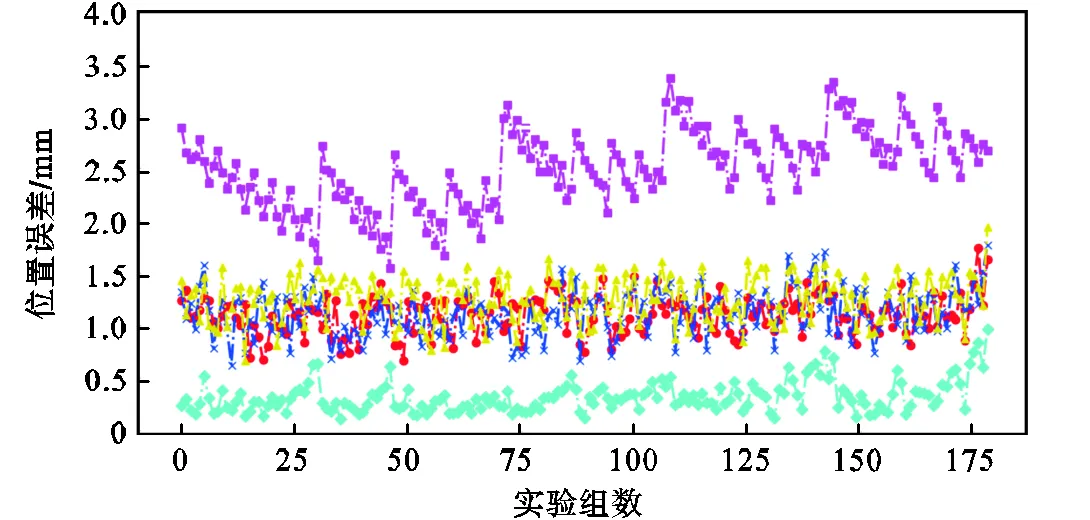
（d）總體位置誤差對比

圖10?位置誤差對比

4?結?論

(1)本文充分考慮了測量坐標系與機器人基坐標系之間的轉換誤差、機器人的運動學誤差以及機器人法蘭端到工具坐標系的測量誤差，使得產生位置誤差的因素更為詳細明確，為接下來的優化算法辨識提供良好支撐．

(2)基于SA算法提出了一種Be-SA算法，通過仿真實驗表明該算法相較于傳統SA算法在工業機器人的運動學誤差參數的辨識上具有更快的收斂速度和更高的尋優精度，且相較于傳統PSO、AFSA算法，改進后的算法同樣具有上述優點．通過實驗表明，機器人的絕對定位精度有了大幅度提升，為拋光學元件奠定了關鍵基礎．

(3)本文的研究未考慮到非運動學參數對位置誤差的影響，因此還需在接下來的研究中弄清楚非運動學誤差相對于空間點位的影響規律，從而還能進一步提高機器人的絕對定位精度．

(4)由于本文只考慮了機器人的位置誤差，忽略了位姿誤差，在加工簡單平面時，會對平面的平面度等造成影響．因此加工簡單平面時使用本方法，還需對位姿誤差做更進一步研究．

［1］ 周?煒，廖文和，田?威. 基于空間插值的工業機器人精度補償方法理論與試驗[J]. 機械工程學報，2013，49(3)：42-48.

Zhou Wei，Liao Wenhe，Tian Wei. Theory and experiment of industrial robot accuracy compensation method based on spatial interpolation[J]. Journal of Mechanical Engineering，2013，49(3)：42-48(in Chinese).

［2］ Joubair A，Bonev I A. Kinematic calibration of a six-axis serial robot using distance and sphere constraints[J]. International Journal of Advanced Manufacturing Technology，2015，77(1/2/3/4)：515-523.

［3］ 齊俊德，張定華，李?山，等. 考慮測量空間的機器人絕對定位精度標定[J]. 機械科學與技術，2020，39(1)：68-73.

Qi Junde，Zhang Dinghua，Li Shan，et al，Calibration of absolute positioning accuracy of robots considering measurement space[J]. Mechanical Science and Technology，2020，39(1)：68-73(in Chinese).

［4］ 朱江新，劉吉剛，田?碩，等. 兩步誤差補償法提高工業機器人絕對定位精度[J]. 機械科學與技術，2020，39(4)：547-553.

Zhu Jiangxin，Liu Jigang，Tian Shuo，et al. Two-step error compensation method for improving absolute positioning accuracy of industrial robots[J]. Mechanical Science and Technology，2020，39(4)：547-553(in Chinese).

［5］ 溫秀蘭，康傳帥，宋愛國，等. 基于全位姿測量優化的機器人精度研究[J]. 儀器儀表學報，2019，40(7)：81-89.

Wen Xiulan，Kang Chuanshuai，Song Aiguo，et al. Study on robot accuracy based on full pose measurement and optimization[J]. Chinese Journal of Scientific Instrument，2019，40(7)：81-89(in Chinese).

［6］ 房立金，黨鵬飛. 基于量子粒子群優化算法的機器人運動學標定方法[J]. 機械工程學報，2016，52(7)：23-30.

Fang Lijin，Dang Pengfei. Kinematic calibration method of robots based on quantum-behaved particle swarm optimization[J]. Journal of Mechanical Engineering，2016，52(7)：23-30(in Chinese).

［7］ Luo Guoyue，Zou Lai，Wang Ziling，et al. A novel kinematic parameters calibration method for industrial robot based on Levenberg-Marquardt and differential evolution hybrid algorithm[J]. Robotics and Computer-Integrated Manufacturing，2021，71：102165.

［8］ Hsiao J C，Shivam K，Lu I F，et al. Positioning accuracy improvement of industrial robots considering configuration and payload effects via a hybrid calibration approach[J]. IEEE Access，2020，8：228992-229005.

［9］ Jiang Yizhou，Yu Liangdong，Jia Huakun，et al. Absolute positioning accuracy improvement in an industrial robot[J]. Sensors，2020，20(16)：4354.

［10］ Yuan Peijiang，Chen Dongdong，Wang Tianmiao，et al. A compensation method based on extreme learning machine to enhance absolute position accuracy for aviation drilling robot[J]. Advances in Mechanical Engineering，2018，10(3)：1687814018763411.

［11］ Denavit J，Hartenberg R S. A kinematic notation for lower-pair mechanisms based on matrices[J]. Journal of Applied Mechanics，1955，77(2)：215-221.

［12］ Qi Junde，Chen Bing，Zhang Dinghua. A calibration method for enhancing robot accuracy through integration of kinematic model and spatial interpolation algorithm[J]. Journal of Mechanisms and Robotics，2021，13(6)：061013.

［13］ Metropolis N，Rosenbluth A W，Rosenbluth M N，et al. Equation of state calculations by fast computing machines[J]. The Journal of Chemical Physics，1953，21(6)：1087-1092.

［14］ ?lhan ?. An improved simulated annealing algorithm with crossover operator for capacitated vehicle routing problem[J]. Swarm and Evolutionary Computation，2021，64：100911.

［15］ 黃?智，劉永超，廖榮杰，等. 基于SSO算法優化神經網絡的數控機床熱誤差建模[J]. 東北大學學報(自然科學版)，2021，42(11)：1569-1578.

Huang Zhi，Liu Yongchao，Liao Rongjie，et al. Thermal error modeling of numerical control machine tools based on neural network by optimized SSO algorithm[J]. Journal of Northeast University(Natural Science Edition)，2021，42(11)：1569-1578(in Chinese).

［16］ Li Xin，Ma Xiaodong. An improved simulated annealing algorithm for interactive multi-objective land resource spatial allocation[J]. Ecological Complexity，2018，36：184-195.

［17］ 韓?龍，張?娜，汝洪芳. 人工智能算法：原理、技巧及應用[M]. 北京：清華大學出版社，2022.

Han Long，Zhang Na，Ru Hongfang. Artificial . Intelligence Algorithm：Principle，Skill and Application[M]. Beijing：Tsinghua University Press，2022(in Chinese).

［18］ 周?煒. 飛機自動化裝配工業機器人精度補償方法與實驗研究[D]. 南京：南京航空航天大學，2012.

Zhou Wei. Compensation Method of Industrial Robot Accuracy and Experimental Research for Aircraft Automated Assembly[D]. Nanjing：Nanjing University of Aeronautics and Astronautics，2012(in Chinese).

Improvement in Absolute Positioning Accuracy of Industrial Robot Based on Improved Simulated Annealing Algorithm

Huang Zhi1，Min Jie1, 2，Chen Guike1，Rao Zhimin3，Xin Qiang3，Zhao Xun3

(1. School of Mechanical and Electrical Engineering，University of Electronic Science and Technology of China，Chengdu 611731，China；2. No. 710 R&D Institute，CSSC，Yichang 443003，China；3. Institute of Optics and Electronics，Chinese Academy of Sciences，Chengdu 610207，China)

Owing to the low absolute positioning accuracy of industrial robots during the polishing of large-diameter optical components，achieving high surface machining accuracy for processing components is challenging. This study proposes a calibration method to construct a comprehensive error model for industrial operating robots by considering multiple error sources，such as the conversion error between the measurement coordinate system and the robot base coordinate system，the kinematic error in the robot，and the measurement error from the robot flange end to the tool coordinate system. Based on the simulated annealing(SA)algorithm，the improved Be-SA algorithm identifies these error parameters. Based on simulation experiments，it can be observed that the improved Be-SA algorithm has a faster convergence speed in identifying error parameters and higher precision compared with the PSO，AFSA，and SA algorithms. Finally，the KUKA robot verification experiment was conducted. Results showed that the average absolute positioning error of the KUKA KR 120 R3900 robot identified using the Be-SA algorithm decreased from 2.497mm to 0.321mm. Moreover，the maximum absolute positioning accuracy decreased from 3.358mm to 0.961mm. This demonstrates that the comprehensive error model constructed herein has good applicability in identifying kinematics error parameters，and the improved Be-SA algorithm can effectively improve the absolute positioning accuracy of the robot，which is an important reference value with respect to the improvement in the grinding and polishing of large-aperture optical components.

industrial robot；absolute positioning accuracy；simulated annealing algorithm；error model

10.11784/tdxbz202208029

TP242

A

0493-2137(2024)04-0374-08

2022-08-21；

2023-03-06.

黃?智（1977—??），男，博士，副教授.

黃?智，zhihuang@uestc.edu.cn.

四川省科技計劃資助項目(2021YFG0078).

the Science and Technology Plan Project of Sichuan Province，China(No. 2021YFG0078)．

(責任編輯：王曉燕)