空冷式多級熱電制冷器性能綜合分析

孫悅桐, 孟凡凱, 周 林, 徐辰欣

(海軍工程大學 動力工程學院,武漢 430033)

熱電制冷又稱溫差電制冷或半導體制冷,可通過帕爾貼效應將電能直接轉化為溫差[1].與傳統的壓縮制冷相比,熱電制冷無運動部件,可靠性高,壽命長、易維護;模塊化特點使其在制冷量增大時沒有顯著的性能損失;無工作流體,可避免泄漏危害環境[2-4].隨著熱電材料技術的迅速發展,熱電制冷技術成為制冷與低溫領域的研究熱點,在微電子系統、激光通信、醫療等領域得到了廣泛應用[5-7].

一些特殊領域的設備需要在低溫環境中維持運行.如基于異質結勢壘型結構的中波紅外探測器工作溫度在150～195 K的范圍內[8];各油庫和油站使用的測定儀器需要滿足300～200 K逐點降溫的要求;X射線太空望遠鏡需要在低溫的狀態下工作,制冷溫度需達到170 K左右[9],進而實現降低噪聲、減弱靈敏度的效果.單級熱電制冷器最大制冷溫差只能達到60 K左右[10],對于更大溫差、更大溫度跨度的場合,單級熱電制冷器無法滿足需求,此時需要采用多級制冷,通過增加級數獲得更大的制冷溫差.

多級熱電制冷即采用垂直級聯(金字塔狀)排列方式,低一級冷端為高一級熱端散熱,由高溫端至低溫端,制冷溫度逐漸降低,低溫級模塊可達到最低制冷溫度[11].隨著溫度跨度的增加,多級熱電制冷器的性能會迅速降低[12],對多熱熱電制冷器性能的分析與優化具有重要意義.Karimi等[13]討論了金字塔型多級制冷器的熱流密度和性能系數最大值,數值模擬結果表明,熱端散熱器的熱阻是決定多級熱電制冷器整體性能的關鍵因素.Parashchuk等[14]開發了一種多級熱電制冷器,利用四級商用模塊和兩級超低溫模塊設計并制作了冷卻樣機,工作溫度可達140 K.Phong和Shih[15]在建模結果與性能尺寸權衡的基礎上構建了多級熱電制冷器的實驗模型,實驗結果顯示,在熱負荷為10 mW的情況下,六級熱電制冷器可達到的溫度差為137 K.Sofradir公司運用四級熱電制冷器生產的處于非常溫運行的面陣規格為320×256的MCT淺制冷型焦平面紅外探測器,該類探測器可在200 K和250 K兩個定點溫度下工作[16].

綜合有關多級熱電制冷的研究可見,一是研究模型中大多未考慮制冷器兩端換熱器件的影響,而外部熱阻有限溫差傳熱引起的不可逆性對制冷性能有很大影響;二是性能指標多為制冷量和制冷系數,缺少協調制冷能力和經濟性能的綜合指標.有限時間熱力學是現代熱力學理論的一個重要分支,實現了熱力學、傳熱學、流體力學和化學反應動力學等多個基礎學科理論的交叉融合,著重研究在有限時間、有限尺寸、有限面積、有限速率傳熱等約束下的各類過程、循環和裝置的最優性能,是分析能量轉換裝置的重要理論與有力工具[17-20],已廣泛應用于化學熱機[21]、燃料電池[22]、布朗熱機[23]、熱電裝置[24]等能量轉換裝置的分析中,得到了一系列不同于傳統分析結果的新結論和一系列更接近實際、更具普適意義的新成果.本文基于有限時間熱力學理論,充分考慮外部熱源與熱電制冷器之間的不可逆性,建立空冷式多級熱電制冷器有限時間熱力學模型,提出協調性能系數評價指標,分析工作電流、熱電臂橫截面積和制冷溫差對裝置性能的影響,可為多級熱電制冷器的結構設計與性能優化提供參考.

1 多級熱電制冷器模型

圖1給出了多級熱電制冷器有限時間熱力學模型.圖中:I為電流.區別于非平衡熱力學模型,本模型考慮了熱電模塊端面與熱源之間的換熱器熱阻,體現出外部有限傳熱面積下的有限速率傳熱不可逆性對裝置性能的影響.裝置主要分為兩個部分:熱電制冷模塊和熱沉.熱電制冷模塊與環境空氣之間的熱量交換通過熱沉完成,并安裝風扇加強換熱.裝置熱電偶總數為M,每個熱電偶由一個P型和一個N型熱電偶臂組成.由高溫端向低溫端各級熱電偶數分別為mi(1≤i≤n).TE為高溫熱源溫度,TL為低溫熱源溫度,熱電制冷器第1級熱端溫度(放熱溫度)和第n級冷端溫度(吸熱溫度)分別為Th和Tc,由第1級冷端至第n級熱端各級間溫度分別為Ti(1≤i≤n-1).高低溫熱源吸放熱量為QE和QL,制冷模塊放、吸熱量分別為Qh和Qc,各節點熱流量分別為Qi(1 ≤i≤n-1).

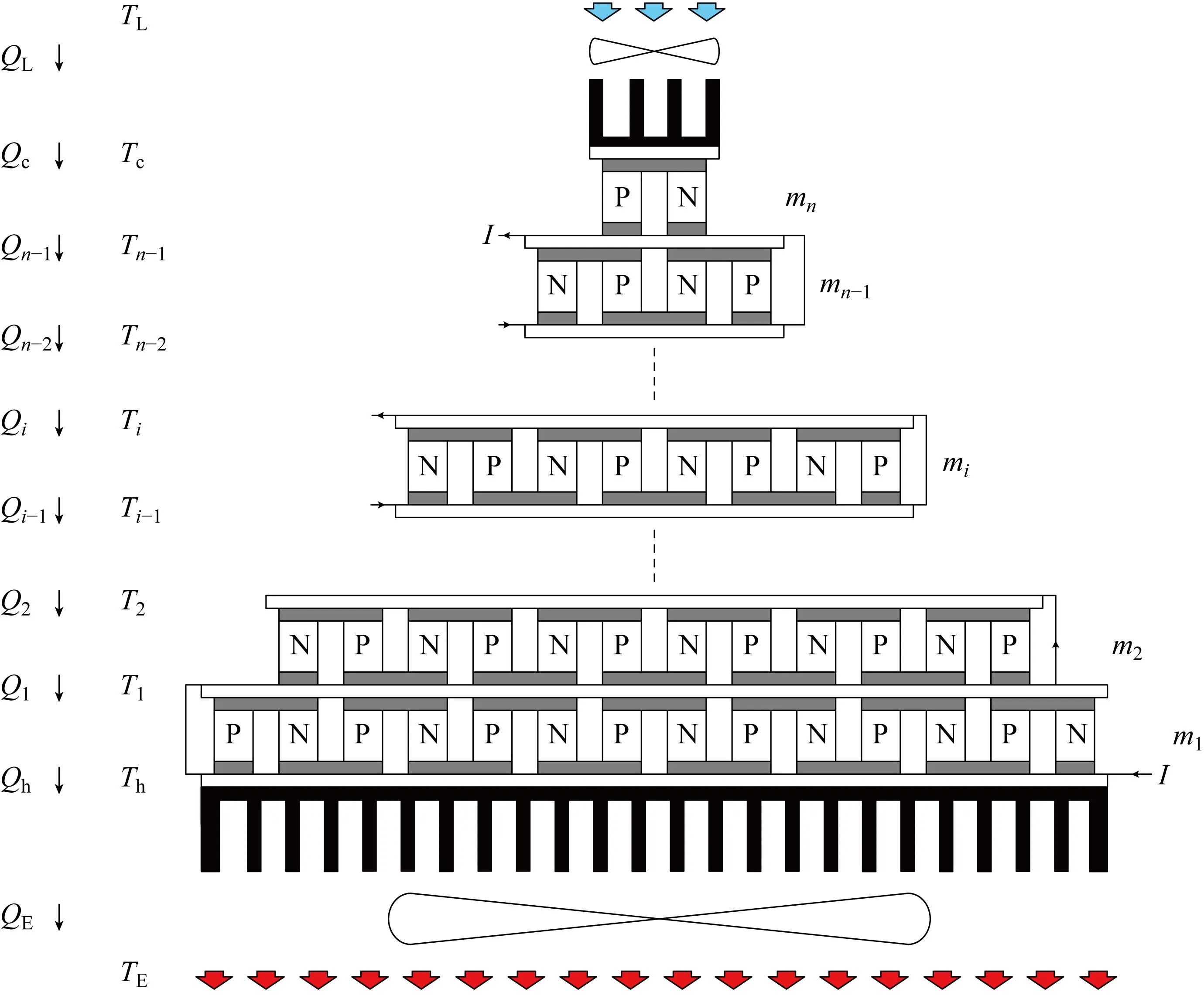
圖1 多級熱電制冷器有限時間熱力學模型Fig.1 Finite time thermodynamic model of multistage thermoelectric cooler

忽略級間熱漏損失,兩級間熱流量等于高一級熱端的散熱量,同時等于低一級冷端的吸熱量.由非平衡熱力學理論,可得由高溫端至低溫端的各節點的熱流量,分別為

Qh=m1[αITh-K(Th-T1)+ 0.5I2R-0.5μI(Th-T1)]

(1)

Q1=m1[αIT1-K(Th-T1)- 0.5I2R+0.5μI(Th-T1)]=m2[αIT1-K(T1-T2)+ 0.5I2R-0.5μI(T1-T2)]

(2)

Qi=mi[αITi-K(Ti-1-Ti)- 0.5I2R+0.5μI(Ti-1-Ti)]=mi+1[αITi-K(Ti-Ti+1)+ 0.5I2R-0.5μI(Ti-Ti+1)] (2≤i≤n-2)

(3)

Qn-1=mn-1[αITn-1-K(Tn-2-Tn-1)- 0.5I2R+0.5μI(Tn-2-Tn-1)]=mn[αITn-1-K(Tn-1-Tc)+ 0.5I2R-0.5μI(Tn-1-Tc)]

(4)

Qc=mn[αITc-K(Tn-1-Tc)- 0.5I2R+0.5μI(Tn-1-Tc)]

(5)

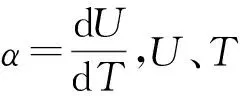
式(2)～(4)可整理成關于未知節點溫度Ti(1≤i≤n-1)的由n-1個方程組成的方程組:

[(m1-m2)(αI-0.5μI)+(m1+m2)K]×T1-m2(K+0.5μI)T2=m1(K-0.5μI)Th+(m1+m2)0.5I2R

(6)

mi(0.5μI-K)Ti-1+[(mi-mi+1)(αI- 0.5μI)+(mi+mi+1)K]Ti-mi+1(K+ 0.5μI)Ti+1=(mi+mi+1)0.5I2R

(7)

mn-1(0.5μI-K)Tn-2+[(mn-1-mn)(αI-

0.5μI)+(mn-1+mn)K]Tn-1=

mn(K+0.5μI)Tc+(mn-1+mn)0.5I2R

(8)

由式(6)～(8)聯立解得中間連接層溫度Ti(1≤i≤n-1)為

(9)

(10)

(11)

考慮熱電模塊兩端與熱源不可逆傳熱的影響,根據有限時間熱力學理論,熱端和冷端的熱流量可分別表示為

(12)

式中:RE和RL分別為熱、冷端的傳熱熱阻.

由能量守恒方程式可得:

Qh=QE,Qc=QL

(13)

聯立式(1)～(5)、(9)～(13),得到熱電制冷器熱、冷端溫度.把Ti(1 ≤i≤n-1)、Th、Tc代入式(1)～(5)得流過各節點的熱流量,可得各級功率為

P1=Qh-Q1

(14)

Pi=Qi-1-Qi(2≤i≤n-1)

(15)

Pn=Qn-1-Qc

(16)

各級制冷系數為

(17)

εi=Qi/Pi(2≤i≤n-1)

(18)

εn=Qc/Pn

(19)

裝置整體的輸入功率和制冷系數分別為

(20)

(21)

2 熱阻分析

冷熱兩端的熱阻包括4個部分:陶瓷基板導熱熱阻Rcp、接觸熱阻Rc、熱沉基板熱阻Rex和熱沉對流換熱熱阻Rcv.式(12)中的RE和RL可表示為上述4個熱阻之和.圖2所示為相應的熱阻網絡圖.圖中:RP和RN分別為P型和N型熱電偶的熱阻.

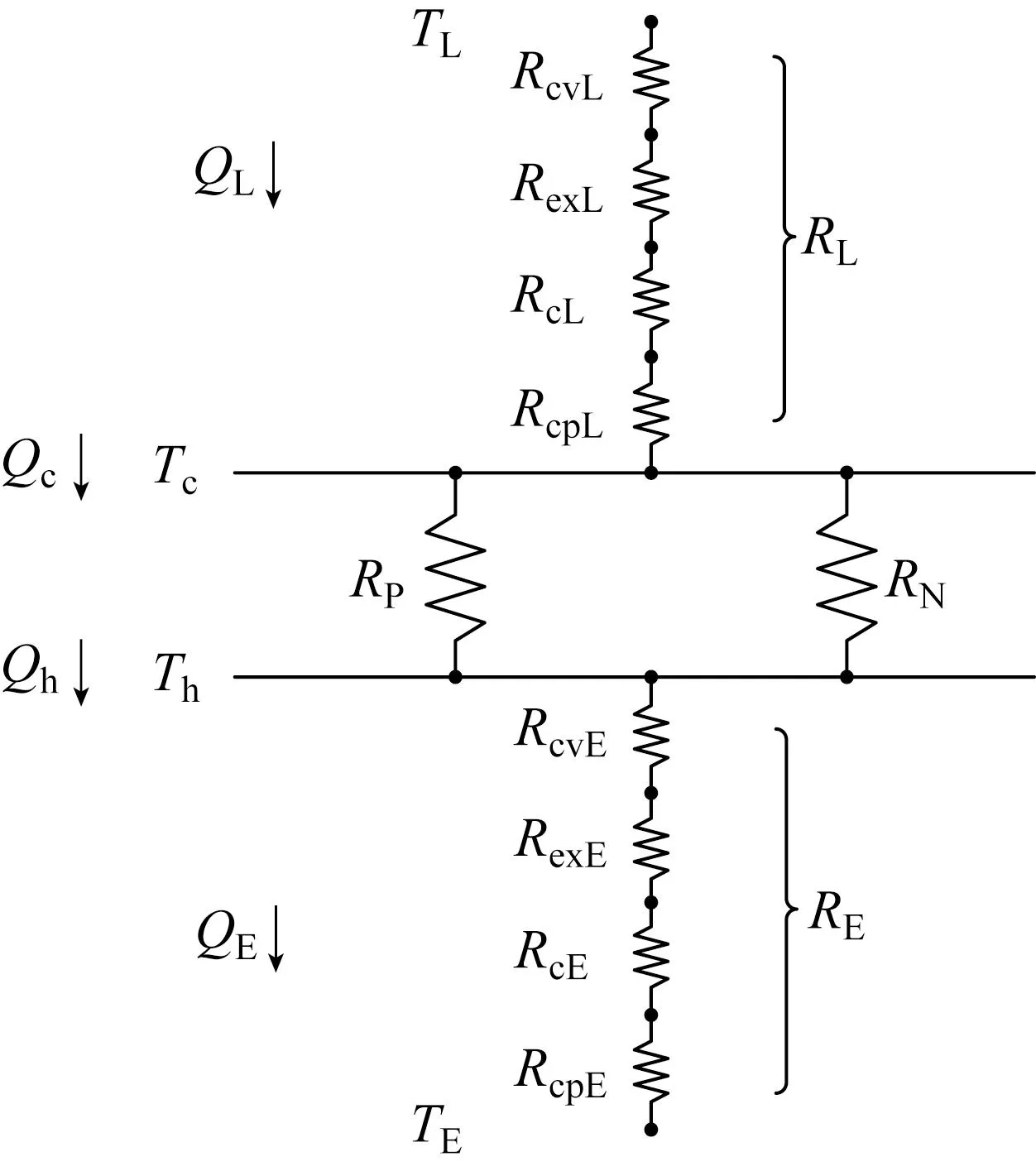
圖2 熱阻網絡Fig.2 Thermal resistance network

模塊的陶瓷基板熱阻、接觸熱阻和熱沉基板熱阻分別為

(22)

式中:δcp、δc和δex分別為陶瓷基板、導熱硅脂和熱沉基板的厚度;Acp、Ac和Aex分別為陶瓷基板、導熱硅脂和熱沉基板的面積;λcp、λc和λex分別為陶瓷、導熱硅脂和熱沉基板的導熱率.

熱電制冷器兩側通過氣體與固體壁面對流換熱,造成熱阻較大,需要采用熱沉和風扇組合強化換熱.本文模型中采用等截面直肋熱沉,其結構如圖3所示.圖中:δr為肋片厚度;br為肋片間距;H為肋片高度;W為肋片長度.

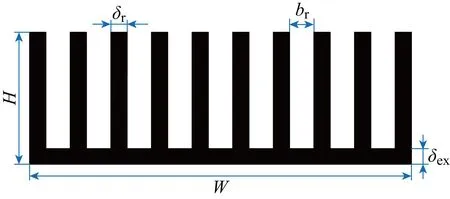
圖3 熱沉結構Fig.3 Structure of heat sink

裝置冷熱兩側空氣為肋壁的強迫風冷,對流換熱熱阻Rcv為[25]

(23)

式中:h1為對流換熱系數;λr為肋片熱導率.

圖4給出了一定工況下,制冷量與制冷系數隨熱端散熱熱阻的變化趨勢.圖中:tE和tL分別為高溫熱源溫度和低溫熱源溫度.當其他參數設定,隨著冷熱兩端散熱熱阻的增大,裝置的制冷量和制冷系數逐漸降低,熱阻大小對制冷性能有著較大影響.因此,本文在熱力學模型中考慮了冷熱源與熱電模塊之間的有限速率傳熱,彌補了現有研究中未考慮制冷器兩端換熱器件外部熱阻有限溫差傳熱引起的不可逆性對制冷性能影響的不足.

圖4 制冷量、制冷系數與熱端熱阻的關系Fig.4 Relationship between cooling capacity, coefficient of performance and thermal resistance at hot end

3 評價指標

3.1 熱力學完善度

制冷系數由設備運行的環境溫度和制冷溫度決定,其數值無法反映出裝置的不可逆程度,在不同環境和制冷溫度條件下也沒有可比性.為了更好地對比反映裝置的性能,馬一太等[26]首次提出熱力學完善度ηre這一評價指標,并將其應用于壓縮式制冷的計算中.熱力學完善度定義為裝置實際的制冷系數ε與同一溫限下逆向卡諾循環制冷系數εc之比,即

(24)

熱力學完善度反映了設備實際狀況與理想循環之間的差距以及不可逆性,可以將不同制冷溫差下的同一制冷裝置或者具有相同運行模式的制冷裝置在相同的基礎上對比研究制冷特性,有助于更全面地反映裝置的制冷特性和不可逆程度.

3.2 協調性能系數

由熱電制冷的性能曲線可知,最大制冷量和最大制冷系數對應不同的最佳電流,制冷能力與制冷的經濟性無法同時達到最優.為了尋求制冷性能的協調,文獻[27]中提出了將制冷量和制冷系數兩個性能指標與各自最大值的比值再線性加權,作為目標函數的雙目標優化數學模型,即

(25)

式中:QLmax為所能達到的最大制冷量;εmax為所能達到的最大制冷系數;x為0～1的比例系數.

系數G體現了制冷量與制冷系數的協調,x的取值大小反映了對這兩個性能指標的偏好.當性能系數G達到最大時,表示一定偏好下制冷量與制冷系數協調達到最佳.

為了體現制冷量與耗功協調性能,定義協調性能系數F:

(26)

式中:Pmax為最大制冷量對應的耗功.

系數F體現了制冷量與耗功的協調,當其取最大值時,意味著取得了兩者的最佳折衷.耗功在一定程度上反映了經濟性能的高低,系數F越大,說明制冷量越接近最大制冷量、同時耗功相對較小,表明了制冷性能和經濟性能越理想.工程應用中,當追求裝置制冷量與經濟性能的統一時,推薦協調性能系數F作為衡量標準;當裝置對制冷量或制冷系數有所偏好,推薦采用協調性能系數G,可對x進行不同的取值.

4 影響參數分析

熱電制冷器選用熱電材料碲化鉍(Bi2Te3),熱電臂橫截面積為A=1.4 mm×1.4 mm,單元長度為L=2 mm.選取熱電五級結構制冷器進行分析,第1級對數為m1=300,隨著級數的增加,熱帶單元對數逐級減半,總的熱電偶對數為582對.材料的物性參數會隨溫度的變化而變化,參數擬合公式[28]如下:

αP=-αN=(22 224.0+930.6T- 0.990 5T2)×10-9

(27)

ρP=ρN=(5 112.0+163.4T+ 0.627 9T2)×10-10

(28)

λP=λN=(62 605.0-277.7T+ 0.413 1T2)×10-4

創始人王勇的命運轉折是改革開放40年中的標志性事件，他從未避諱自己的出身，在多次采訪中，均表示自己本是鄒平電業局的一個臨時工。或許是進入體制無望，或許是時代創業浪潮的吸引，也或許是一個偶然的機遇，1986年，36歲的王勇離開電業局當選西王村支部書記，開始在西王村創辦企業。

(29)

μP=-μN=(930.6T-1.981T2)×10-9

(30)

式中:αj、ρj、λj和μj(j=P, N)分別表示材料的塞貝克系數、電阻率、熱導率和湯姆遜系數.冷熱兩端換熱器一般為鋁制,文中討論溫度范圍內熱導率變化較小,取為定值λex=222 W/(m·K);空氣比熱容、熱導率等物性參數取相應熱源溫度下的取值.

數值計算中,熱電材料物性中的定性溫度采用熱端與冷端的平均溫度.熱端為300 K、冷端為213 K時,熱電材料物性參數計算結果分別為:塞貝克系數為 1.957 6 V/K;電阻率為 8.833 5 Ω/m;熱導率為 1.855 4 W/(m·K);湯姆遜系數為 1.083 6 V/K.

4.1 工作電流的影響

圖5和圖6分別給出了不同低溫熱源溫度下裝置的制冷量QL和制冷系數ε隨工作電流的變化趨勢.由圖可見,當電流在0.8～2.8 A的范圍內,隨著電流的增大,制冷量和制冷系數都呈現先增大后減小的趨勢,存在最佳電流,但是兩者的變化情況有所不同.當低溫熱源溫度為-60 ℃ 時,制冷量最大為2.245 W,對應的最佳工作電流為2.55 A;電流為1.3 A時對應最大的ε為0.059.最大的QL和ε對應的最佳電流相差較大,說明制冷能力與經濟性能無法同時達到最優.隨著制冷溫度的降低,QL和ε均減小.相較于低溫熱源溫度為-50 ℃ 來說,溫度降低10 ℃,對應的最大QL和ε分別降低了19.18%和29.37%,溫度降低20 ℃,對應的最大QL和ε分別降低了38.21%和52.21%.小電流時,焦耳熱效應的影響很小可忽略不計,但由于熱量與電流的平方呈正比,隨著電流的增加,對制冷量和制冷效率的影響逐漸凸顯,導致QL和ε存在最大值而后開始降低.隨著低溫熱源溫度的降低,QL取最大值所對應的最佳工作電流基本保持不變,ε取最大值所對應的最佳工作電流隨之增大.由圖6可以發現,相同的ε對應兩個不同的工作電流,考慮到制冷量可知,當ε相同時選擇大電流可以獲得更好的制冷能力.

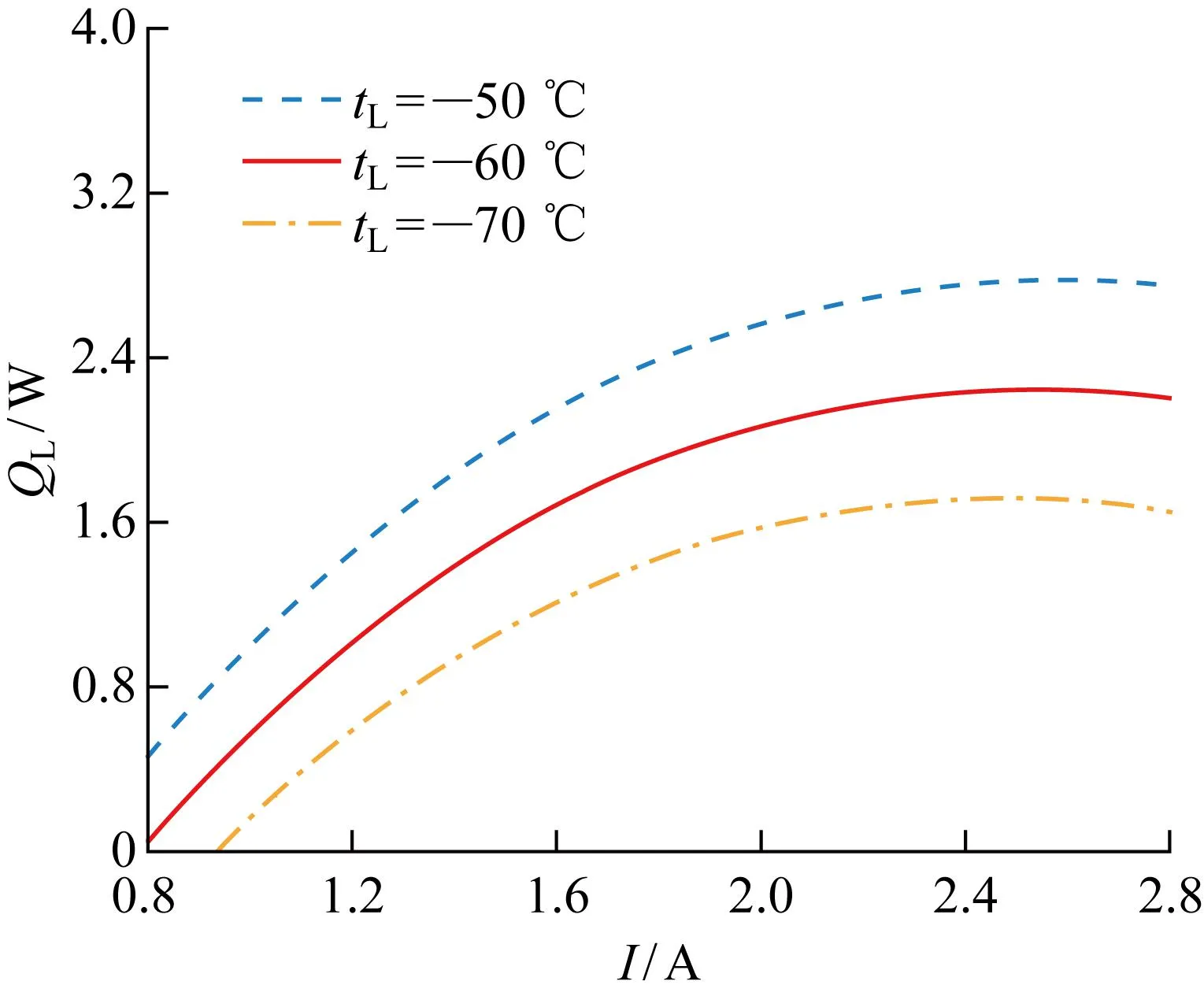
圖5 不同制冷溫度下制冷量與工作電流關系Fig.5 Relationship between cooling capacity and working current at different cooling temperatures

圖7給出了不同低溫熱源溫度下熱力學完善度ηre與工作電流I的關系.熱力學完善度隨電流的變化趨勢與ε相同,其值反映了裝置的不可逆程度,可以排除其他的影響因素直接進行比較.當低溫熱源溫度為-50 ℃ 時,熱力學完善度隨電流的增加先增大后減小,在I=1.15 A時取最大值為 0.028 8,對應的工作電流稱為最佳工作電流.當tL=-60 ℃時,熱力學完善度在I=1.3 A時取最大值為 0.024 1,相較tL=-50 ℃ 降低了16.44%;當tL=-70 ℃ 時,熱力學完善度在I=1.5 A時取最大值為0.019 0,相較tL=-50 ℃ 降低了33.86%.隨著低溫熱源溫度的降低,ηre取最大值所對應的最佳工作電流也隨之增大.與圖6的結果對比表明,不同制冷溫差下,εmax的變化相較ηremax的變化更大,因為ηre是個相對值,可以更直觀地反映出不同制冷溫差下裝置的性能,能夠直接進行比較的優點使得引入熱力學完善度這一評價指標有著重要意義.圖8給出了最大制冷溫差與電流的關系.由圖可知,最大制冷溫差隨著工作電流的增大呈現先增大后減小的趨勢,存在最佳電流使得制冷溫差達到最大.當電流為2.35 A時,制冷溫差取最大值為129 ℃.結果表明,采用多級熱電制冷可以獲得較低的制冷溫度,實現大溫差制冷,在需要低溫工作環境的設備中具有廣泛應用前景.

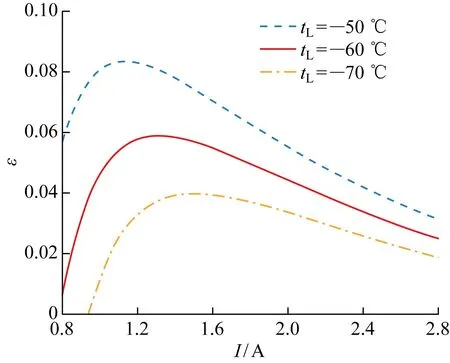
圖6 不同制冷溫度下制冷系數與工作電流關系Fig.6 Relationship between coefficient of performance and working current at different cooling temperatures

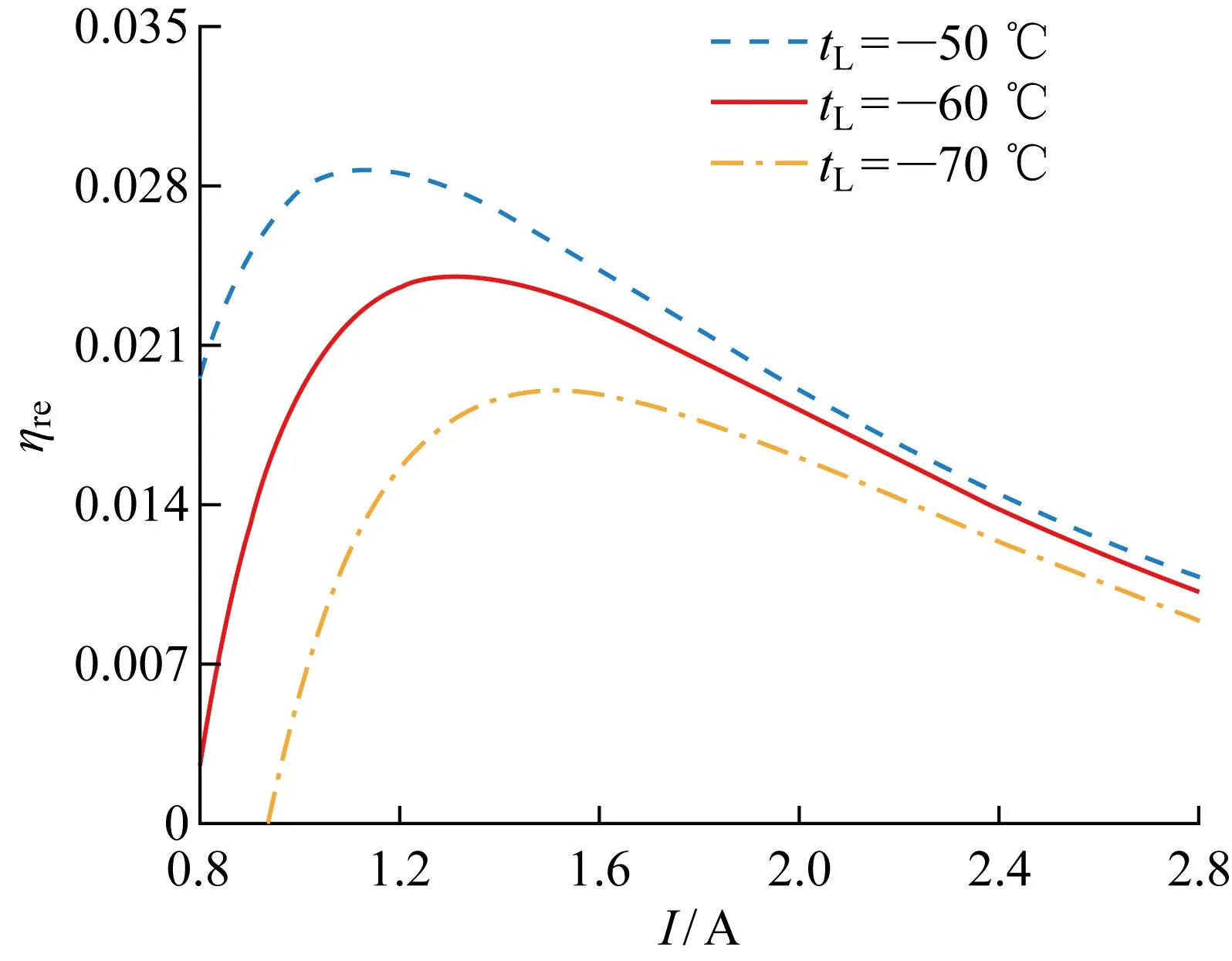
圖7 不同制冷溫度下熱力學完善度與工作電流關系Fig.7 Relationship between thermodynamic perfection and working current at different cooling temperatures

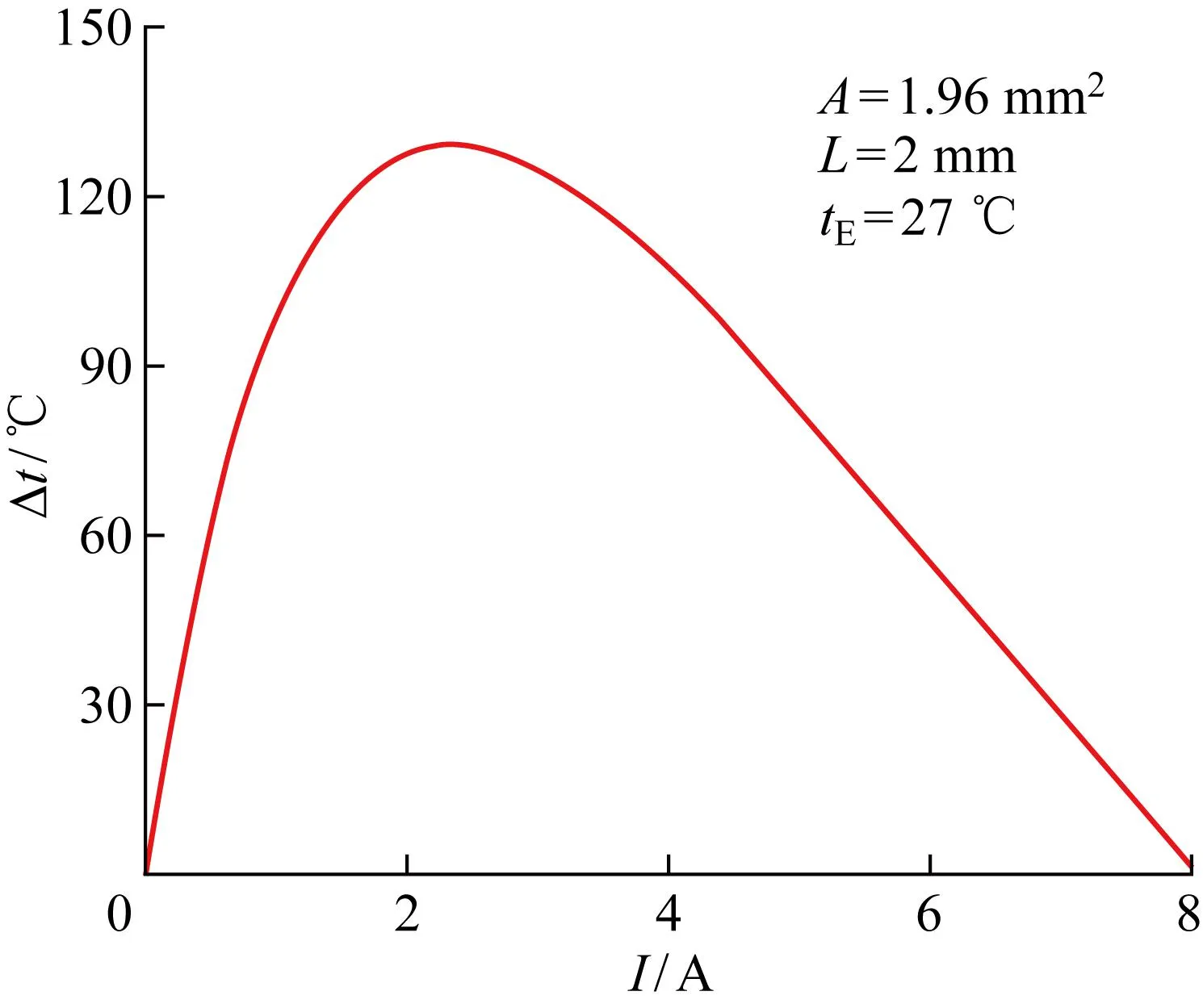
圖8 最大制冷溫差與工作電流的關系Fig.8 Relationship between maximum cooling temperature difference and working current

圖9所示為不同低溫熱源溫度下協調性能系數與工作電流的關系.圖9(a)體現了制冷量與耗功的協調,當系數達到最大時表示一定工作條件下獲得最佳折衷.系數F隨著工作電流的增加呈現先增大后減小的趨勢,結果表明存在最佳工作電流使得F取最大值.當tL=-50 ℃ 時,在I=1.6 A時F取最大值為0.371,相較于tL=-60 ℃和tL=-70 ℃ 時的最大值分別增加了12.21%和31.64%.隨著低溫熱源溫度的降低,系數F取最大值所對應的最佳工作電流也隨之增大.圖9(b)表示通過權衡尋找制冷量和制冷系數的全局最優,本文取x=0.5進行計算.系數G隨著工作電流的增加呈現先迅速增大后緩慢減小的趨勢,存在最佳工作電流使得G取最大值.當tL=-70 ℃時,在I=1.9 A時G取最大值為0.885,相較于tL=-60 ℃ 和tL=-50 ℃ 時的最大值分別增加了4.37%和9.38%,結果表明低溫熱源溫度對系數G的影響較小,且當電流到達一定大小后對系數的影響效果較小.通過與圖5和圖6對比可以看出,G取得最大值的工作電流位于QLmax和εmax對應工作電流的中間,此時制冷量與制冷系數獲得最佳折衷,可以實現綜合效益最大化,充分體現了協調性能系數對雙目標的協調意義,為熱電裝置運行工況的選擇提供理論參考.

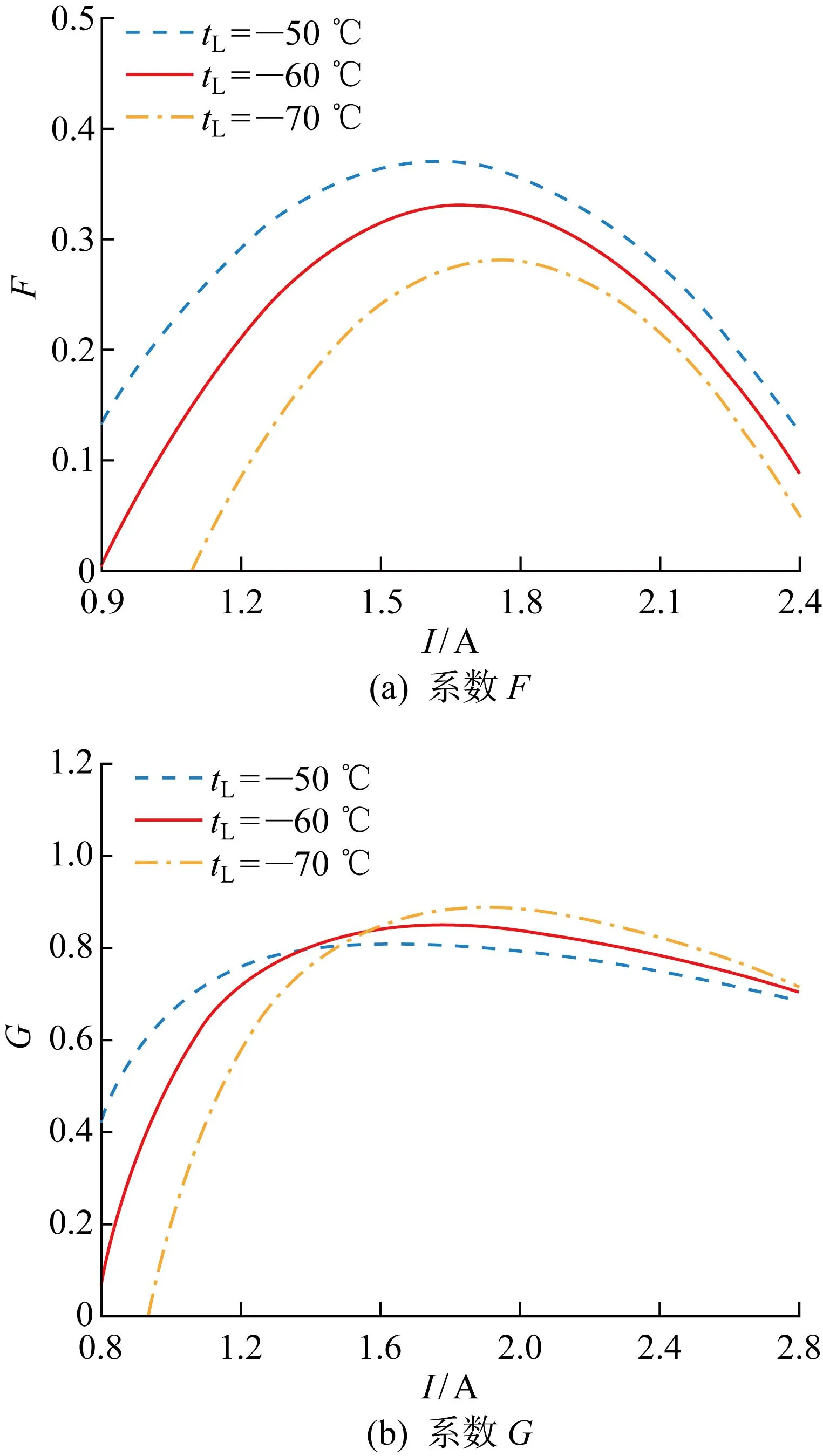
圖9 不同制冷溫度下協調性能系數與工作電流關系Fig.9 Relationship between coordination performance coefficient and working current at different cooling temperatures

4.2 熱電臂橫截面積的影響

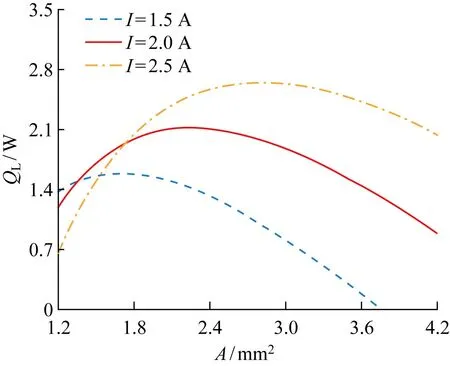
圖10 不同工作電流下制冷量與橫截面積關系Fig.10 Relationship between cooling capacity and cross-sectional area at different working currents

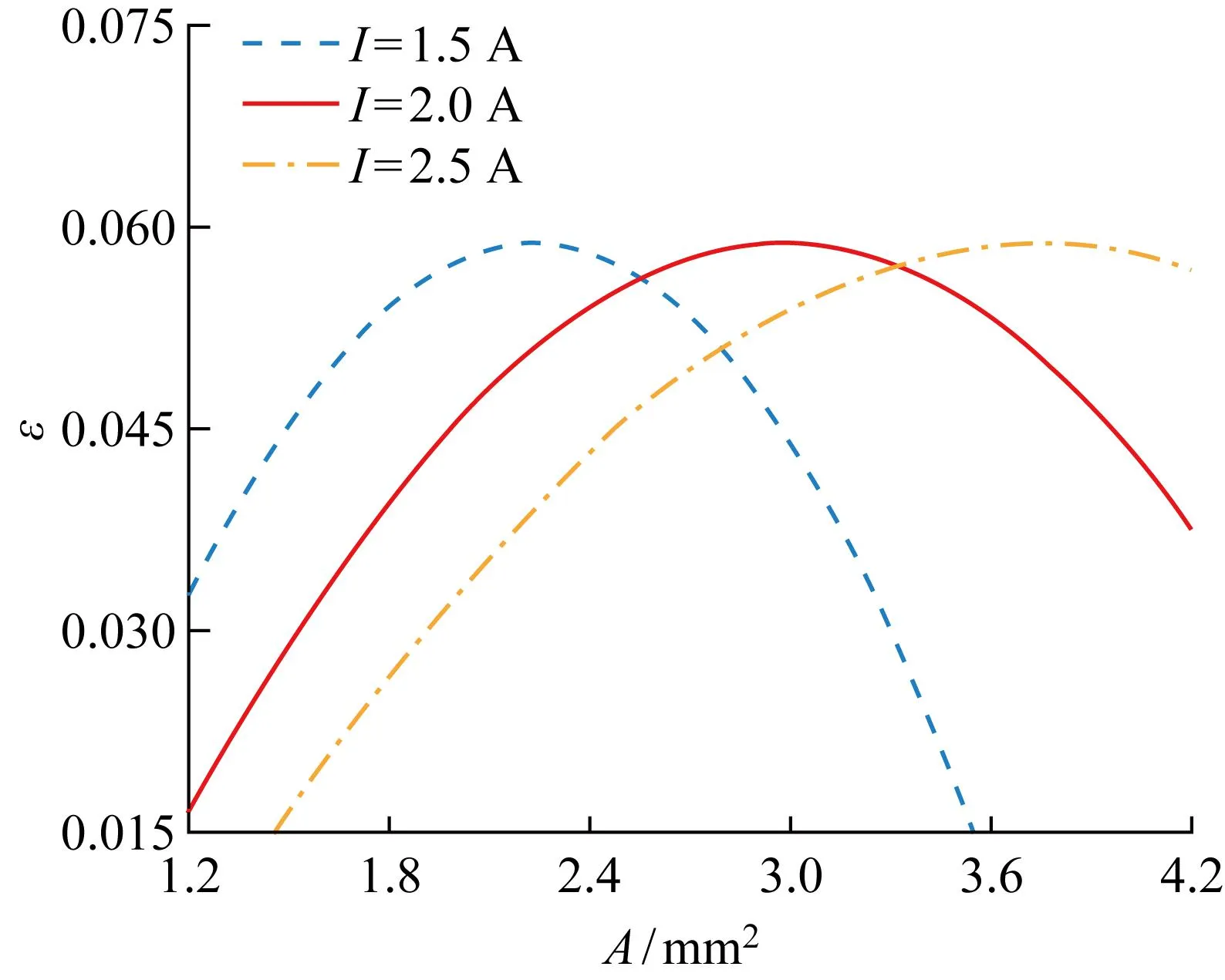
圖11 不同工作電流下制冷系數與橫截面積關系Fig.11 Relationship between coefficient of performance and cross-sectional area at different working currents

圖12所示為不同工作電流下熱力學完善度ηre與橫截面積A的關系.熱力學完善度隨橫截面積的變化趨勢與制冷系數相同,但是在數值上相差較大,結果表明熱電裝置的不可逆程度較大.隨著工作電流的增大,最大ηre對應的最佳橫截面積增大.工作電流I=1.5 A時,橫截面積A=2.2 mm2時熱力學完善度ηre取最大值為0.024;當I取2 A和2.5 A時,最大熱力學完善度ηre對應的最佳橫截面積分別為3.0 mm2和3.7 mm2.

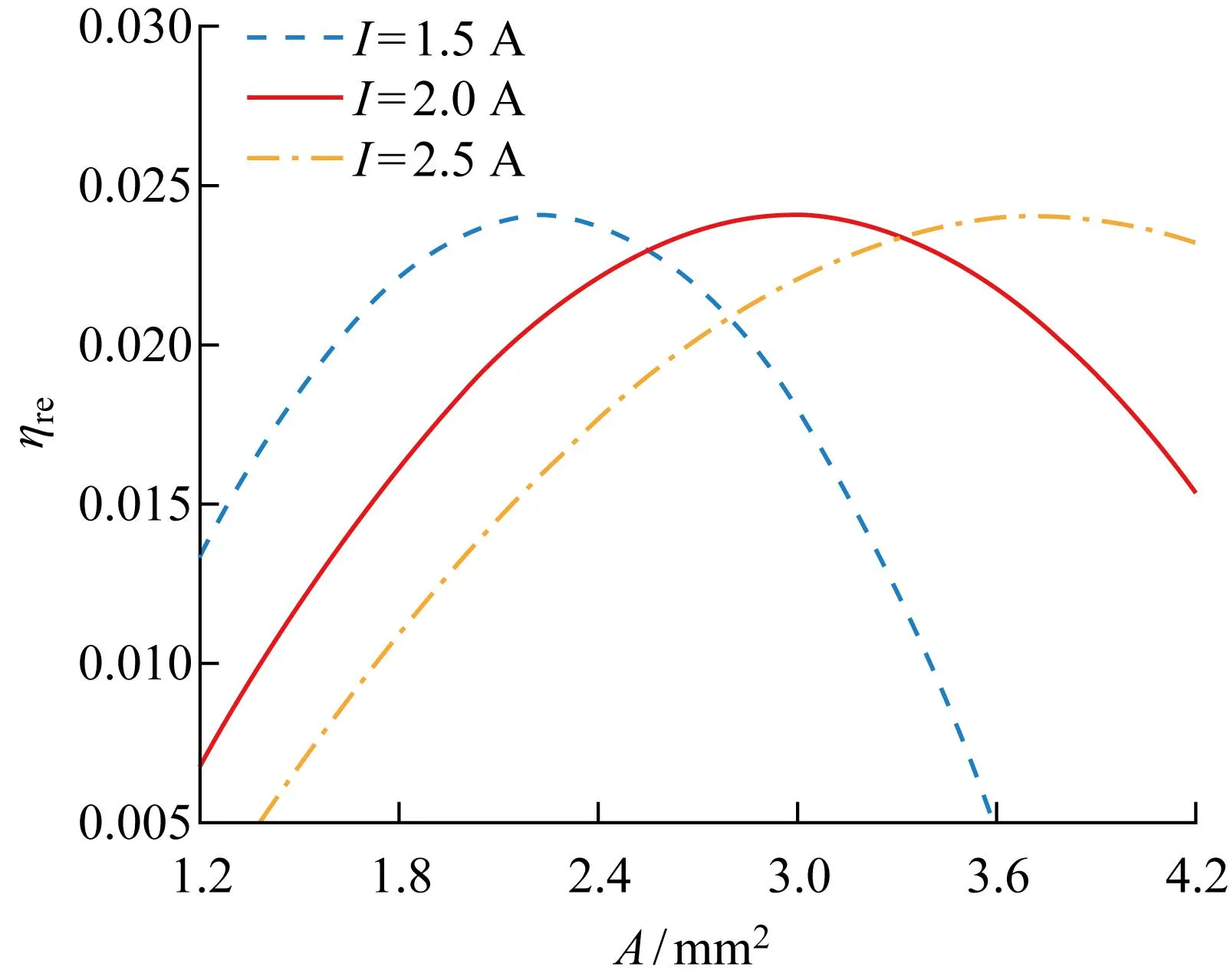
圖12 不同工作電流下熱力學完善度與橫截面積關系Fig.12 Relationship between thermodynamic perfection and cross-sectional area at different working currents

圖13所示為不同工作電流下協調性能系數與橫截面積的關系.圖13(a)中系數F隨著橫截面積的增加呈現先迅速增大后較為緩慢減小的趨勢.工作電流I=1.5 A時,橫截面積A=1.8 mm2時系數F取最大值為0.330.結果表明,通過協調存在最佳橫截面積使得制冷量與裝置耗功獲得最佳折衷.圖13(b)中系數G隨著橫截面積的增加呈現先增大后減小的趨勢,存在最佳橫截面積使G取最大值.工作電流I=1.5 A,橫截面積A=1.7 mm2時系數G取最大值為0.848;當I取2 A和2.5 A時,F和G的最大值對應的最佳橫截面積分別為2.2 mm2和2.8 mm2.結果表明,通過賦予權重可以使制冷量與制冷系數之間有一個很好的權衡,有效協調兩者之間因為橫截面積變化而出現此消彼長的矛盾.

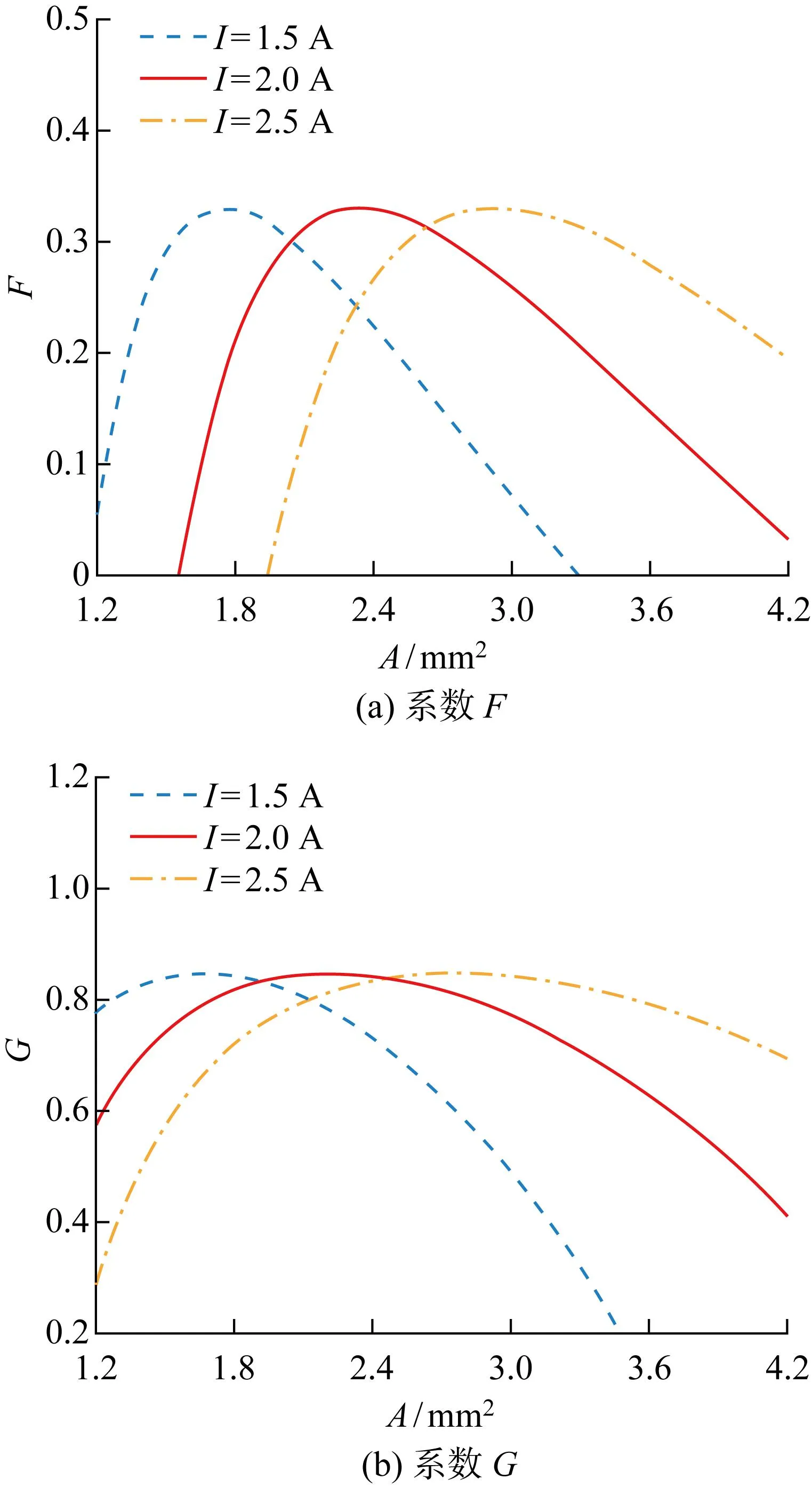
圖13 不同工作電流下協調性能系數與橫截面積關系Fig.13 Relationship between coordination performance coefficient and cross-sectional area at different working currents

4.3 制冷溫差的影響

圖14和圖15分別給出了不同工作電流下裝置的制冷量QL和制冷系數ε隨制冷溫差Δt的變化趨勢.由圖可以發現,當制冷溫差在60～120 ℃的范圍內,當I一定時,制冷量和制冷系數隨著Δt的增大呈現單調減小的趨勢.由于溫差的不斷增大,平均溫度降低,熱電模塊的物性參數發生改變,造成制冷量的不斷下降.圖16所示為不同工作電流下熱力學完善度ηre與制冷溫差Δt的關系.工作電流I=2.5 A時,制冷溫差Δt=78 ℃時熱力學完善度ηre取最大值為0.013;當I取2 A和1.5 A時,制冷溫差分別為78 ℃和70 ℃時對應ηre的最大值,分別為0.019和0.026,相比I=2.5 A條件下的最大ηre分別增大了42.2%和96.6%.結果表明,熱力學完善度隨制冷溫差的增大呈現先緩慢增大后減小的趨勢,與制冷量和制冷系數的變化趨勢有所不同,存在最佳制冷溫差使得熱力學完善度最大,即不可逆程度達到最小.這是由于對于給定的環境溫度,逆卡諾循環制冷系數εc=TE/Δt-1與溫差呈反比關系,熱電制冷器制冷系數與溫差呈類拋物線關系,導致存在最佳溫差使得熱電制冷器制冷系數最接近逆卡諾循環制冷系數,即熱力學完善度最大.這個指標獨立于制冷量和制冷系數,為系統的評價與優化提供了更全面的理論基礎.

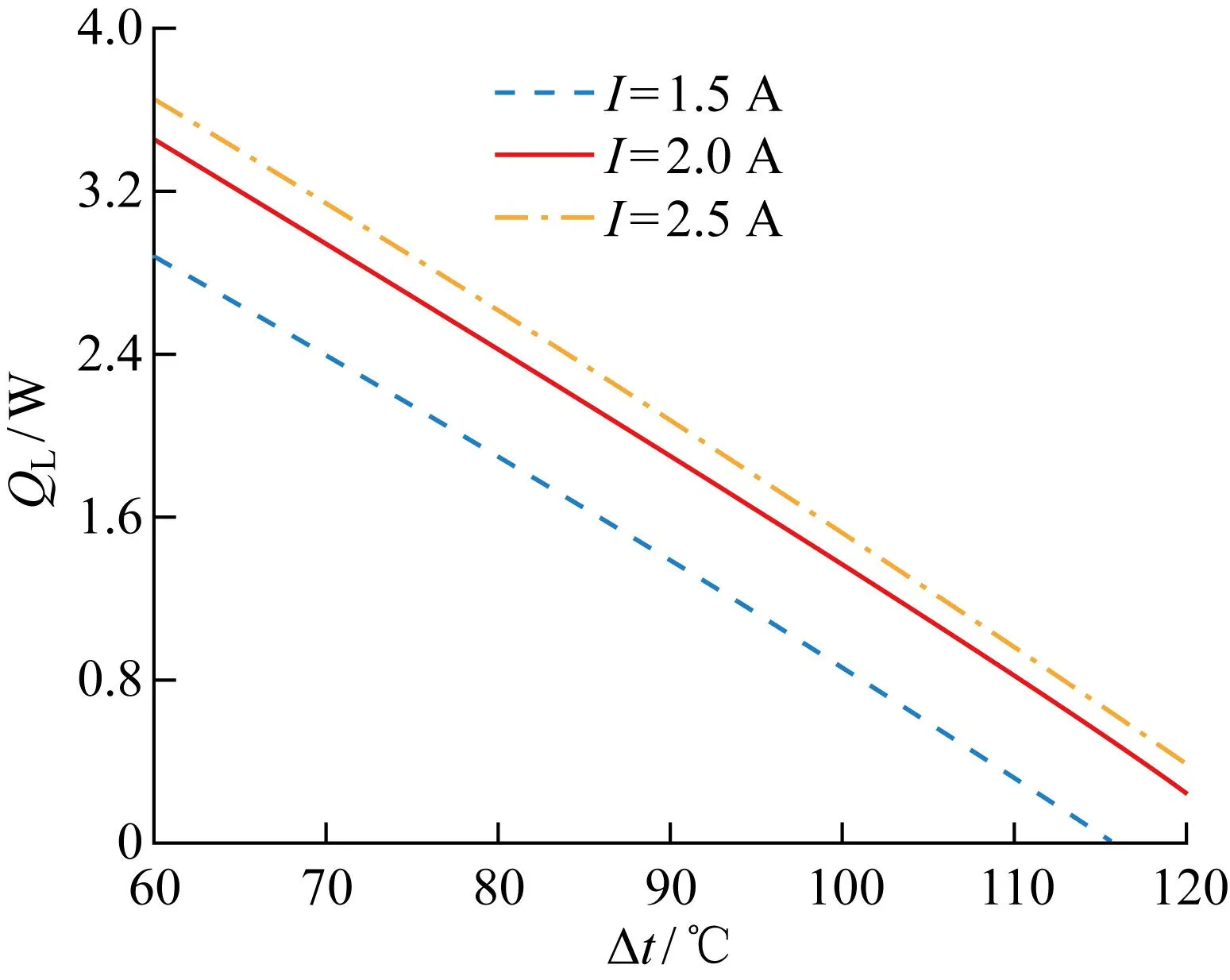
圖14 不同工作電流下制冷量與制冷溫差關系Fig.14 Relationship between cooling capacity and temperature difference at different working currents

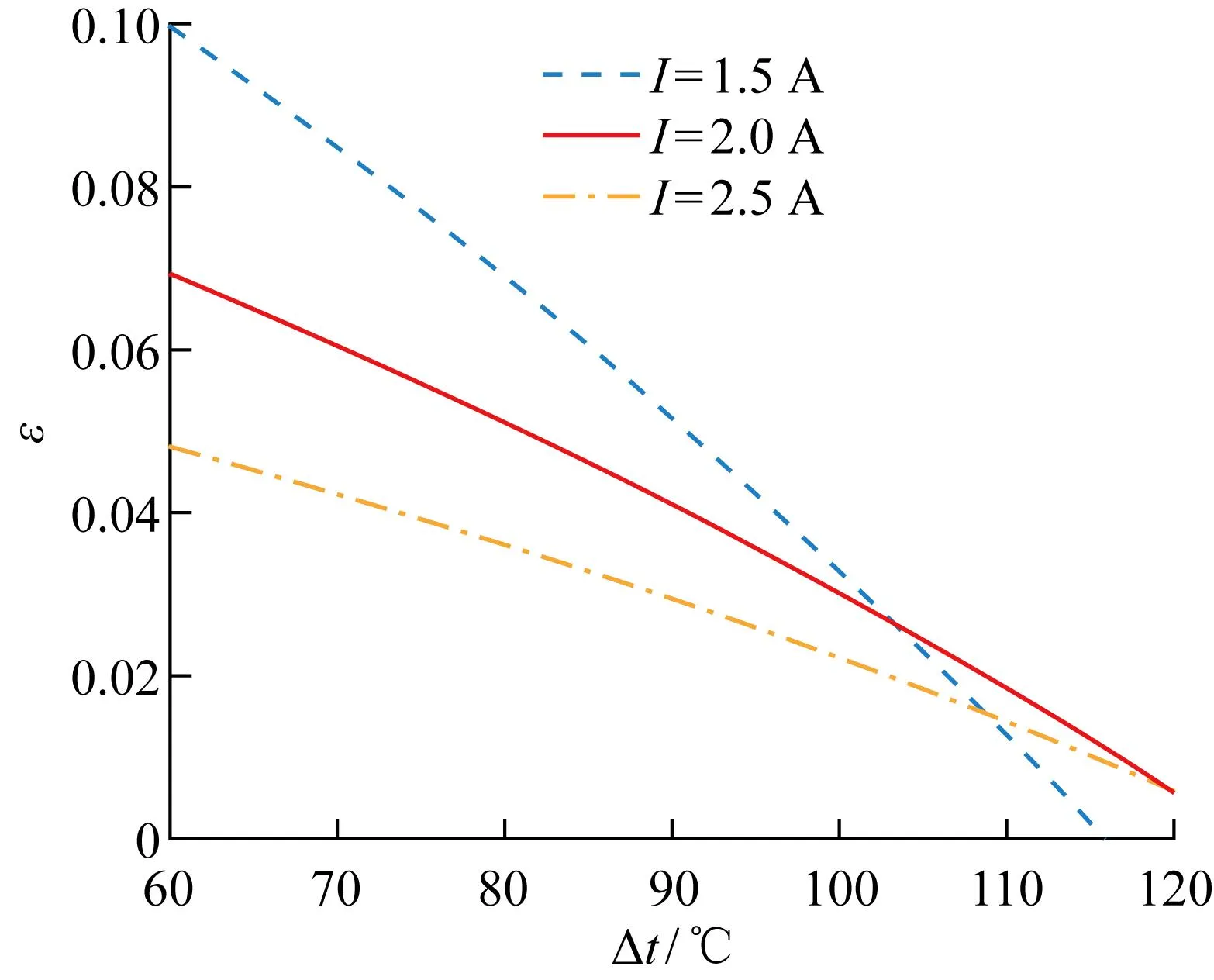
圖15 不同工作電流下制冷系數與制冷溫差關系Fig.15 Relationship between coefficient of performance and temperature difference at different working currents

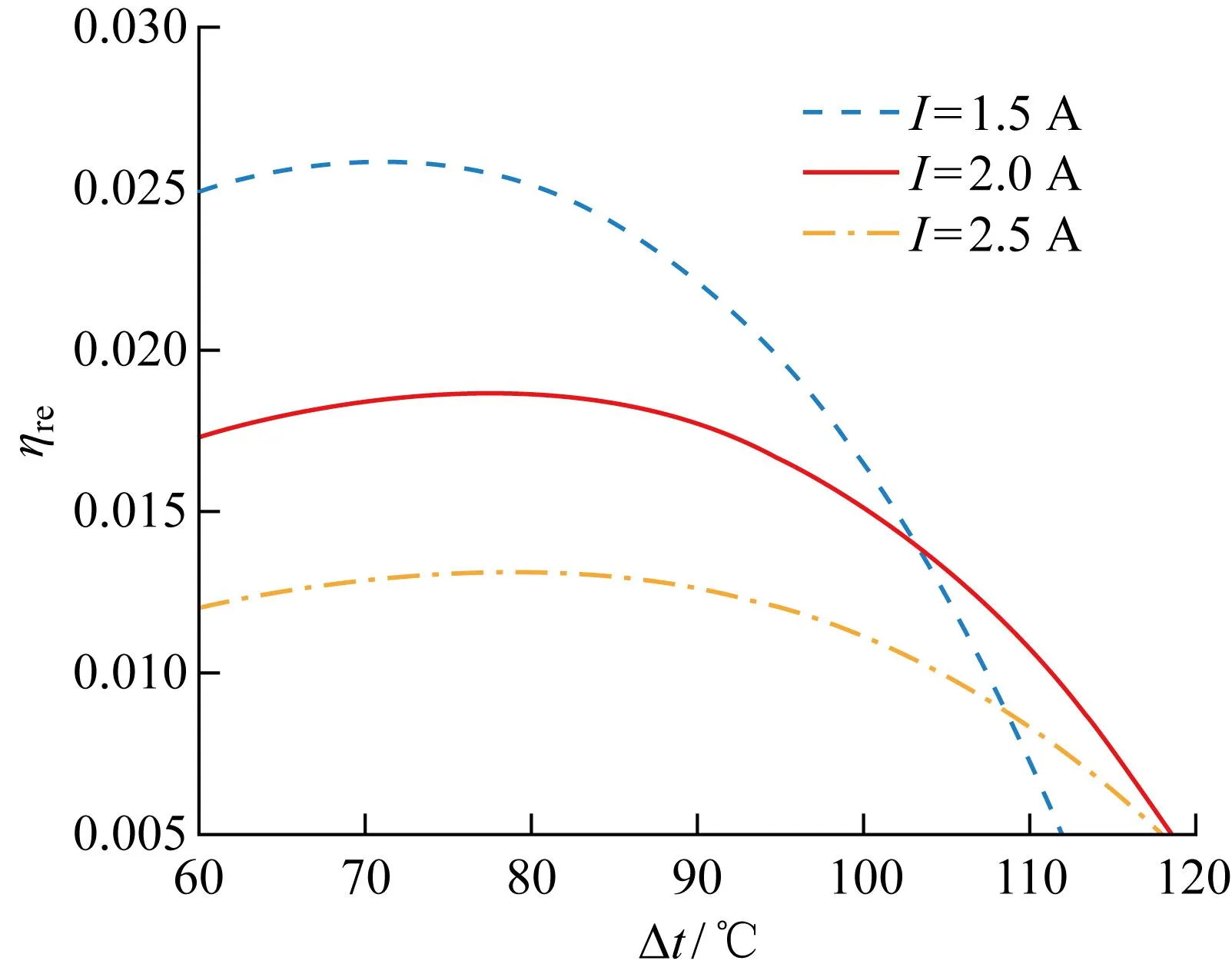
圖16 不同工作電流下熱力學完善度與制冷溫差關系Fig.16 Relationship between thermodynamic perfection and temperature difference at different working currents

5 結論

基于有限時間熱力學理論,建立了空冷式多級熱電制冷器熱力學模型,提出了新的性能評價指標,分析了工作電流、熱電臂橫截面積和制冷溫差對裝置性能的影響,主要結論有:

(1) 當制冷溫差為87 ℃時,工作電流分別為2.55 A和1.30 A,制冷量和制冷系數可分別達到最大值2.245 W和0.059;協調性能系數能夠將制冷量、制冷系數和耗功進行協調后得到綜合性能的最佳折衷,獲得最佳運行參數.電流分別為1.70 A 和1.75 A時,協調性能系數F和G分別取得最大值,獲得制冷量、耗功與制冷系數的最佳折衷.

(2) 一定工況下存在最佳熱電臂橫截面積對應最優的評價指標,超過最佳值后,由于模塊電阻和熱阻減小、模塊產熱量和熱漏量增大,制冷性能降低.綜合考慮制冷能力和經濟性能的協調,當工作電流為2 A時,最佳橫截面積為2～3 mm2.

(3) 制冷量和制冷系數隨制冷溫差增大逐漸減小;熱力學完善度隨制冷溫差增大呈現先增大后減小的趨勢,即存在最佳制冷溫差使得熱力學完善度最大,系統不可逆程度最小.