柔度法測算三點彎曲試樣疲勞裂紋長度的影響因素

高宇昊, 王 佳, 朱官朋, 房 坤, 翟建飛

(中國船舶集團有限公司第七二五研究所, 洛陽 471023)

在疲勞裂紋擴展速率等試驗過程中,采用柔度法可以快捷有效地對裂紋長度進行測算,其基本原理為：對于特定形狀的標準試樣,由解析法計算出的無量綱彈性柔度EBV/F(E為彈性模量;B為試樣厚度;V為裂紋嘴張開位移;F為載荷)和歸一化裂紋長度a/W(a為裂紋長度;W為試樣寬度)可以用某一函數關系來表達。以三點彎曲試樣為例,對應裂紋嘴張開位移的柔度函數如式(1),(2)所示。

3.2141U3+51.516U4-113.03U5

(1)

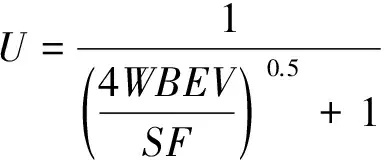
(2)

式中：S為跨距,S=4W;V/F為柔度;U為計算中間量。

測量并計算裂紋嘴張開位移與載荷的關系V/F,可以獲得裂紋的長度,從而實現裂紋長度的自動測算。然而在實際使用時,試樣形狀、測量誤差、彈性模量取值等因素會使測算裂紋長度與真實裂紋長度之間存在偏差[1],余圣甫等[2]在進行單試樣法積分-裂紋擴展量阻力曲線測試時發現,用柔度法測算的裂紋長度比用讀數顯微鏡通過九點法測量的裂紋長度小。張亞軍[3]在對10MnNi3MoV船用結構鋼進行疲勞裂紋擴展速率試驗時發現,試驗開始時用柔度法推導的彈性模量比鋼材彈性模量的典型值低,在柔度函數中使用不同的彈性模量會影響疲勞裂紋擴展速率的試驗結果。柔度法測算裂紋長度的精確性與柔度的測量誤差、彈性模量、刀口尺寸以及引伸計的安裝等因素有關。

一般認為,隨著試樣厚度的增加,裂紋尖端平面應變狀態的比例增加,試樣的有效彈性模量E′將介于平面應力狀態下彈性模量E和平面應變狀態下彈性模量E/(1-ν2)之間(ν為泊松比),從而影響式(1)中的無量綱彈性柔度EBV/F。由于疲勞裂紋擴展速率試樣的裂紋前緣近似呈圓弧狀,僅測量表面裂紋無法反映實際的裂紋長度。筆者針對不同厚度的三點彎曲試樣,在疲勞裂紋擴展速率試驗過程中,利用著色劑[4]在不同裂紋擴展階段對實際裂紋長度進行標記,從而獲得柔度法測算裂紋長度與實際裂紋長度的對應關系,進而分析試樣厚度、柔度函數關系式的適用條件、材料的彈性模量、裂紋前緣彎曲程度(曲率)、引伸計測量標距等因素對柔度法測算裂紋長度的影響。

1 試驗方法

將10Ni6CrCuMoV鋼板(板厚為30 mm)按照GB/T 6398—2017 《金屬材料 疲勞試驗 疲勞裂紋擴展方法》的要求加工成不同厚度的三點彎曲試樣,取樣位置為板厚中心處,試樣長度方向垂直于軋制方向。利用電液伺服疲勞試驗機對試樣進行疲勞裂紋擴展速率試驗,每組3個平行試樣,試樣公稱尺寸及試驗參數如表1所示。

表1 試樣公稱尺寸及試驗參數

首先,在缺口試樣上測量試樣柔度V/F,用疲勞裂紋擴展速率試驗最大載荷的0.9倍(0.9Fmax)對試樣進行彎曲加載-卸載,為了保證加載的穩定性,加載-卸載周期為10 s,連續加載10次,記錄載荷F和對應裂紋嘴張開位移V的值。柔度測量時的載荷-時間曲線如圖1所示。

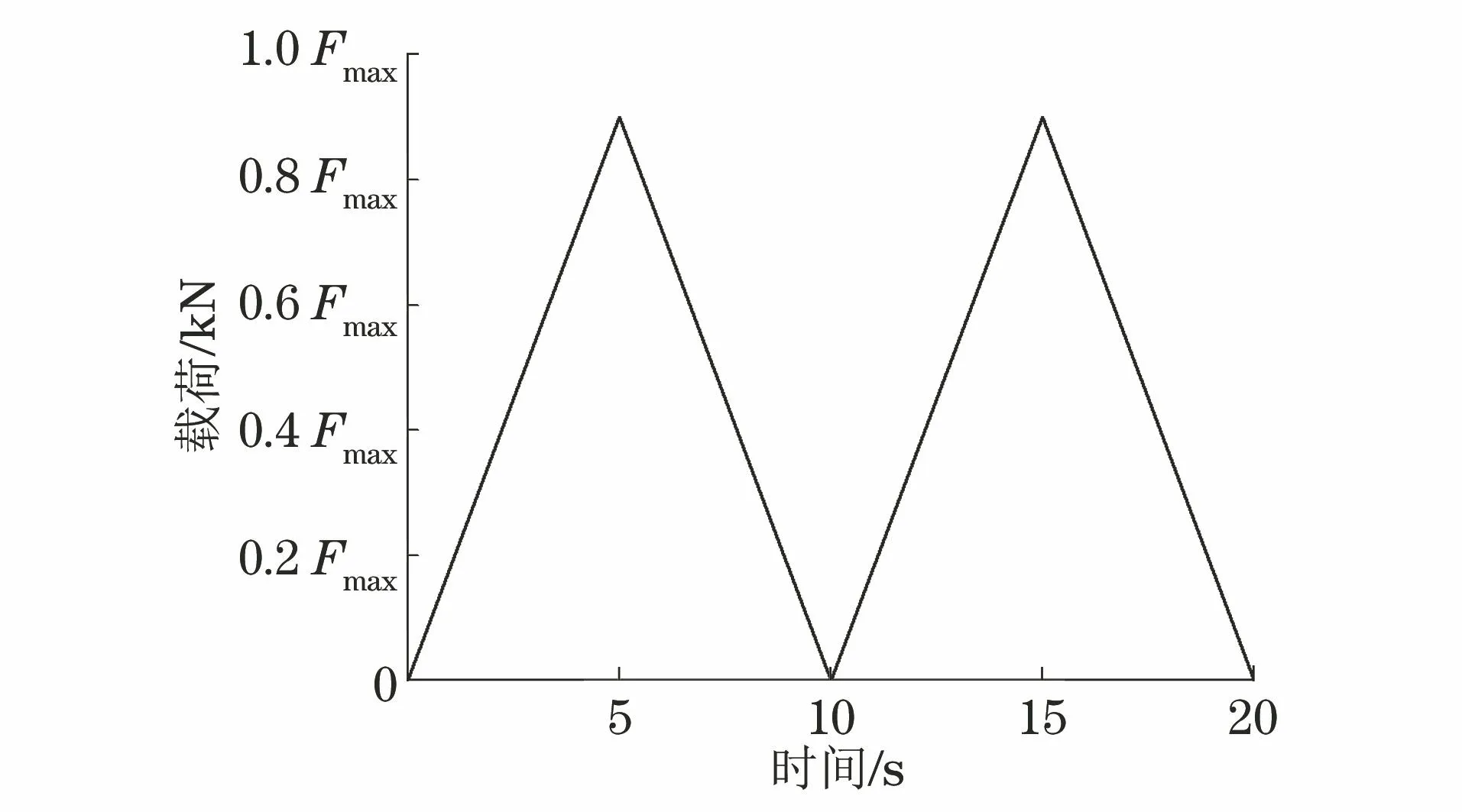
圖1 柔度測量時的載荷-時間曲線

接著在試樣上預制疲勞裂紋,方法為降K(應力強度因子)法,設置最終階段的應力強度因子最大值Kmax為28.0 MPa·m0.5,直至預制裂紋長度aa達到0.2W。用圖1所示的載荷測量試樣柔度,同時從試樣缺口處將著色劑滴入裂紋面,裂紋張開時,顏色分子因毛細作用沉積在裂紋尖端,干燥后完成對預制裂紋的標記。

然后進行疲勞裂紋擴展試驗,方法恒載荷法,當裂紋長度達到約0.3W(ab)時,暫停試驗,用圖1所示的載荷測量試樣柔度,并用著色劑標記裂紋。干燥后繼續進行試驗,當裂紋長度達到約0.4W(ac)、0.5W(ad)、0.6W(ae)、0.7W(af)時,用同樣的操作測量試樣柔度并標記對應裂紋。

最后,試樣在裂紋擴展的最后階段發生彎曲失效,將試樣沿裂紋面打開,用顯微鏡測量標記的裂紋長度。

2 試驗結果

柔度測量時采用末5次循環的載荷F和裂紋嘴張開位移V,在最大載荷的50%～90%對V-F曲線求斜率,以獲得試樣的柔度,根據柔度函數關系式測算裂紋的長度,測算使用的彈性模量為鋼鐵材料典型值206 GPa。以試樣3(厚度為20 mm)為例,不同裂紋長度下的V-F曲線如圖2所示。由圖2可知：隨著裂紋長度的增大,試樣柔度V/F增大,當裂紋長度達到約0.7W時,加載柔度和卸載柔度有明顯區別,此時試樣裂紋尖端已經有較明顯的塑性變形,試樣不再是近似理想的彈性體,會對柔度函數關系造成一定影響。

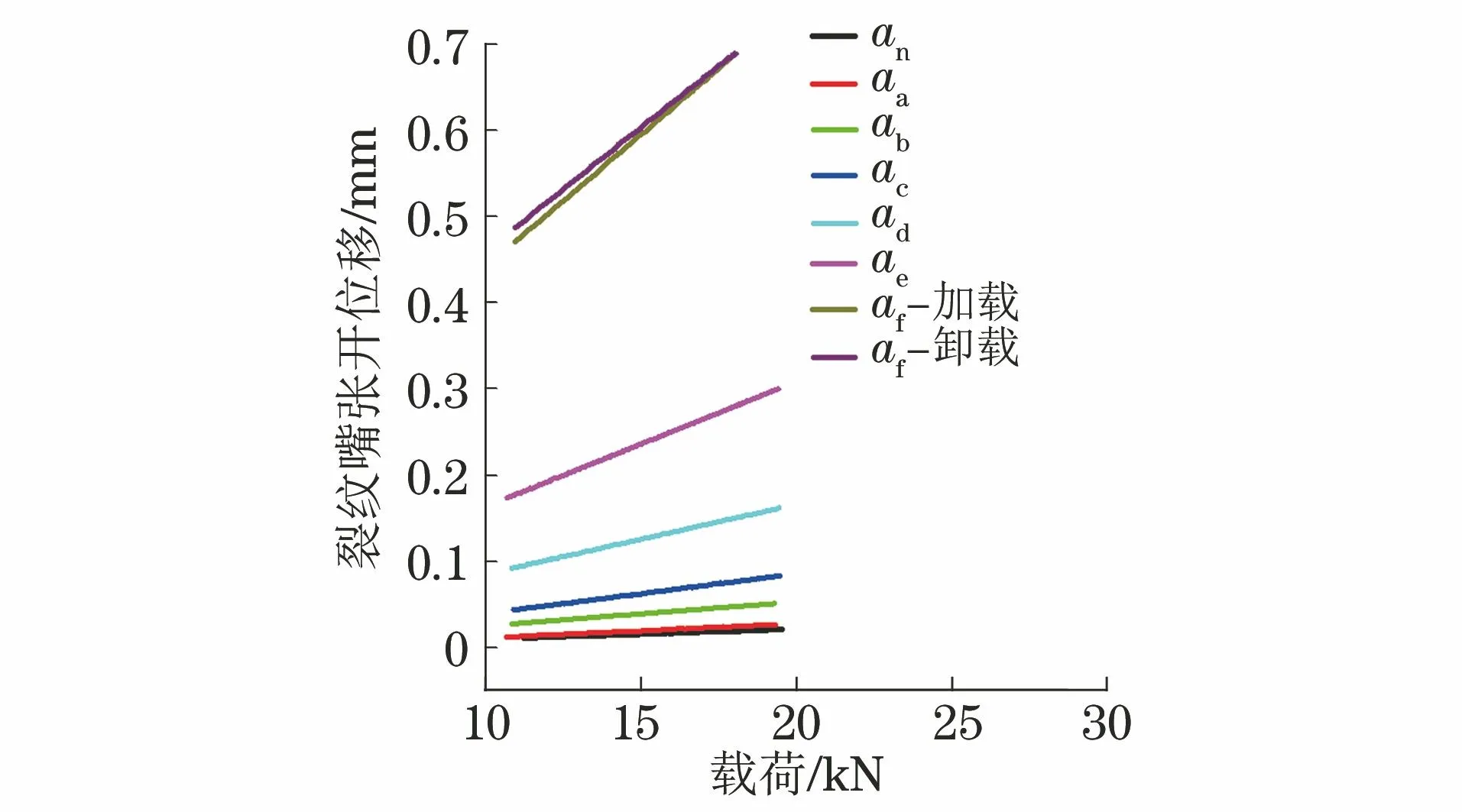
圖2 試樣3在不同裂紋長度下的V-F曲線

采用九點法在顯微鏡下觀察試樣斷口,測量并計算對應的實際裂紋長度,試樣3斷口的宏觀形貌如圖3所示。測量裂紋長度、實際裂紋長度a′和柔度法測算裂紋長度a(1)結果如表2所示。其他試樣斷口的宏觀形貌、裂紋長度測量及測算方法與試樣3相同,其中試樣1(厚度為10 mm)的尺寸較小,在裂紋長度達到0.7W之前就發生了失效。

圖3 試樣3斷口的宏觀形貌

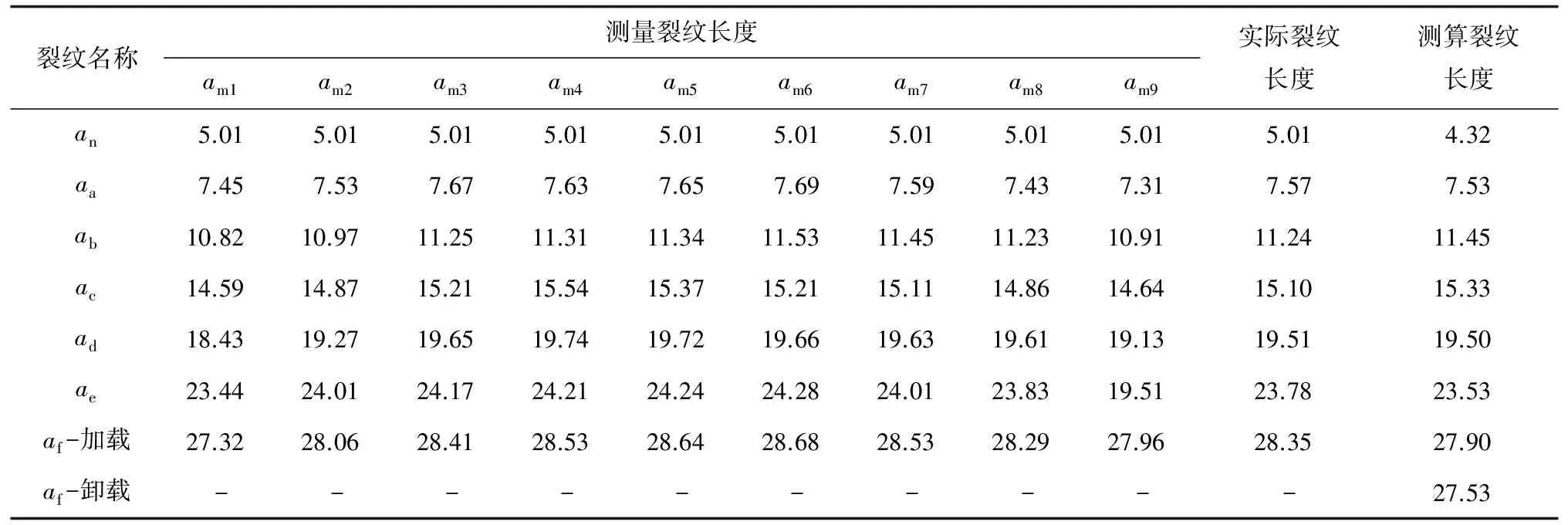
表2 試樣3裂紋長度測量結果 mm

由表2可知：柔度法測算裂紋長度與實際裂紋長度之間存在一定的差異,當裂紋長度達到約0.7W(af)時,加載柔度測算的裂紋長度比卸載柔度測算的裂紋長度稍大,且更接近實際裂紋長度。其他試樣在裂紋長度達到約0.7W(af)時,加載柔度測算的裂紋長度也更接近實際裂紋長度,因此當裂紋長度達到約0.7W(af)時,采用加載柔度來進行裂紋長度的測算。

3 測算裂紋長度的影響因素

使用柔度法測算裂紋長度a(1)與實際裂紋長度a′的差值來反映柔度法測算裂紋長度的準確性。為了與柔度函數關系式對照,將a(1)和a′進行歸一化處理,不同厚度的試樣歸一化裂紋長度差值[a(1)/W-a′/W]/(a′/W)與歸一化實際裂紋長度a′/W的關系如圖4所示。由圖4可知：當厚度相同時,隨著歸一化實際裂紋長度的增大,歸一化裂紋長度差值的絕對值快速減小,當歸一化實際裂紋長度不小于0.3時,歸一化裂紋長度差值的變化趨于平緩;當歸一化實際裂紋長度小于0.3時,隨著試樣厚度的增大,歸一化裂紋長度差值由大變小,柔度法測算裂紋長度與實際裂紋長度相比先偏大后偏小;當歸一化實際裂紋長度不小于0.3,試樣厚度不大于的25 mm時,a(1)與a′相差小于5%,認為a(1)有較好準確性;當試樣厚度為30 mm時,a(1)比a′偏小,相差大于5%,柔度法測算的裂紋長度與實際裂紋長度有較大偏差。

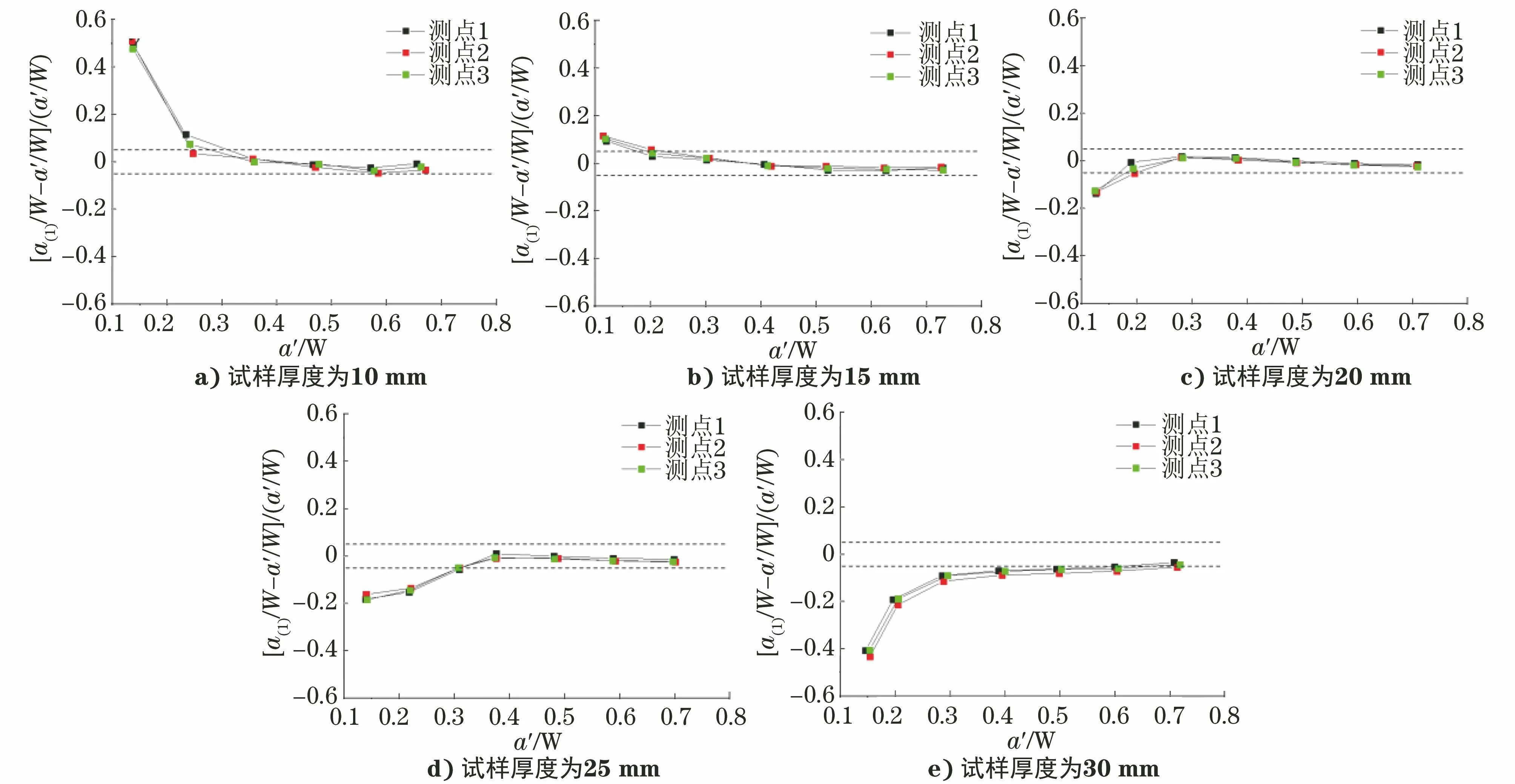
圖4 歸一化裂紋長度差值與歸一化實際裂紋長度的關系

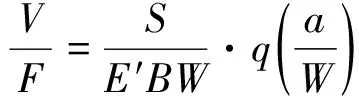
(3)

3.1 柔度函數關系式的適用條件

ASTM E399-22StandardTestMethodforLinear-ElasticPlane-StrainFractureToughnessofMetallicMaterials附錄中指出,三點彎曲試樣裂紋嘴張開位移柔度與裂紋長度的關系如式(3),(4)所示。

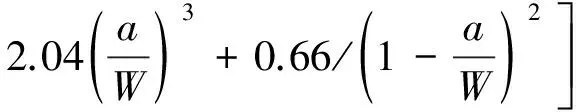
(4)

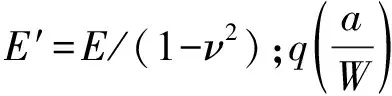
當0≤a/W≤1時,式(3),(4)的精確度不大于1%;當0.3≤a/W≤0.9時,式(3),(4)與式(1),(2)的等價程度不大于0.05%[7]。因此,若以a/W為自變量,當0.3≤a/W≤0.9時,式(1)可作為式(3)的近似解。由于式(1)與式(3)相比更便于計算,因此將式(1)作為常用柔度函數關系式。

以式(3)中的a(3)/W為自變量,經過計算,a(1)/W與a(3)/W的差值[a(1)/W-a(3)/W]/(a(3)/W)與a(3)/W的關系如圖5所示。由圖5可知：當a(3)/W≤0.2時,a(1)/W比a(3)/W明顯偏小,當a(3)/W=0.15時,差值約為17%,隨著a(3)/W的增加,差值快速減小;當a(3)/W≥0.3時,差值小于0.5%。因此,根據柔度函數關系式的適用條件,使用式(1)進行裂紋長度測算時,要求實際裂紋長度a′/W≥0.3是保證測算結果準確的必要條件。

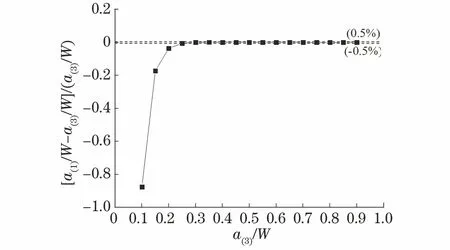
圖5 差值[a(1)/W- a(3)/W]/(a(3)/W)與a(3)/W的關系

3.2 有限元方法對柔度函數關系的模擬

利用有限元分析軟件對三點彎曲試樣的柔度函數關系進行模擬,由于三點彎曲試樣和載荷具有對稱性,故取試樣的一半建立模型,并進行靜力學分析。模型主體采用六面體網格,并對裂紋尖端區域進行網格細化,三維模型的網格類型為C3D20R單元(20節點六面體二次減縮積分實體單元),網格尺寸約為1.0 mm。假設材料的彈性模量為206 GPa,泊松比為0.3,施加載荷如表1所示。試樣整體處于彈性狀態,使用圍線積分方式模擬計算裂紋尖端的應力狀態,模擬的平直裂紋長度為as,根據裂紋嘴中心處的節點坐標變化計算裂紋嘴張開位移。

根據式(1)和有限元模擬的(V/F)s值,求出對應的a(3)/W,借助數學軟件求解出對應的a(4)/W值。在模擬不同裂紋長度as時,不同厚度試樣的差值[a(1)/W-as/W]/(as/W)和[a(3)/W-as/W]/(as/W)與as/W的關系如圖6所示。由圖6可知：當as/W≤0.2時,a(1)/W與as/W差值大于5%;當as/W≥0.3時,a(1)/W與as/W差值小于2%;當as/W≤0.2時,a(3)/W與as/W差值比a(1)/W與as/W差值明顯偏小;當as/W≥0.3時,a(3)/W與as/W差值小于2%;當as/W≥0.3時,柔度函數關系式與有限元模擬結果較為符合,側面驗證了柔度函數關系的正確性。

圖6 兩柔度公式測算裂紋長度與模擬裂紋長度的關系

當試樣厚度不大于40 mm時,在平直貫穿型裂紋情況下,裂紋中心的平面應變狀態對柔度函數關系沒有明顯的影響,當as/W≥0.3時,在式(1)中使用材料的彈性模量E進行計算,可以獲得較準確的測算裂紋長度。

3.3 裂紋曲率對柔度法測算裂紋長度的影響

在金屬材料的疲勞裂紋擴展速率試驗中,裂紋中心處的材料處于平面應變狀態,承受的應力比試樣兩側的應力大,因此中心處的裂紋擴展速率較快,兩側的裂紋擴展速率較慢,裂紋前緣類似圓弧狀。用圓弧近似裂紋前緣的形狀,根據最大裂紋長度amax、最小裂紋長度amin與試樣厚度B之間的幾何關系,裂紋前緣的彎曲半徑R,圓弧角度2α的計算關系分別如式(5)～(7)所示。

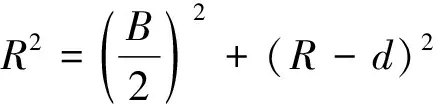
(5)

d=amax-amin

(6)

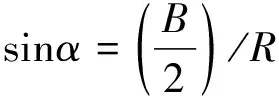
(7)

根據式(5)～(7)和試驗結果,計算當a/W約為0.4時,不同厚度試樣的amax-amin值、曲率半徑R和圓弧角度2α,結果如表3所示。曲率半徑R隨試樣厚度的變化如圖7所示,圓弧角度2α隨試樣厚度的變化如圖8所示。由圖7,8可知：隨著試樣厚度的增大,裂紋的曲率半徑R增大,但增大趨勢并不明顯;隨著試樣厚度的增大,圓弧角度2α增大,且具有明顯的增長趨勢。圓弧角度2α不但與曲率半徑R有關,還有試樣厚度有關,因此對于不同厚度的試樣,圓弧角度2α比曲率半徑R更能近似地描述裂紋前緣的彎曲程度。

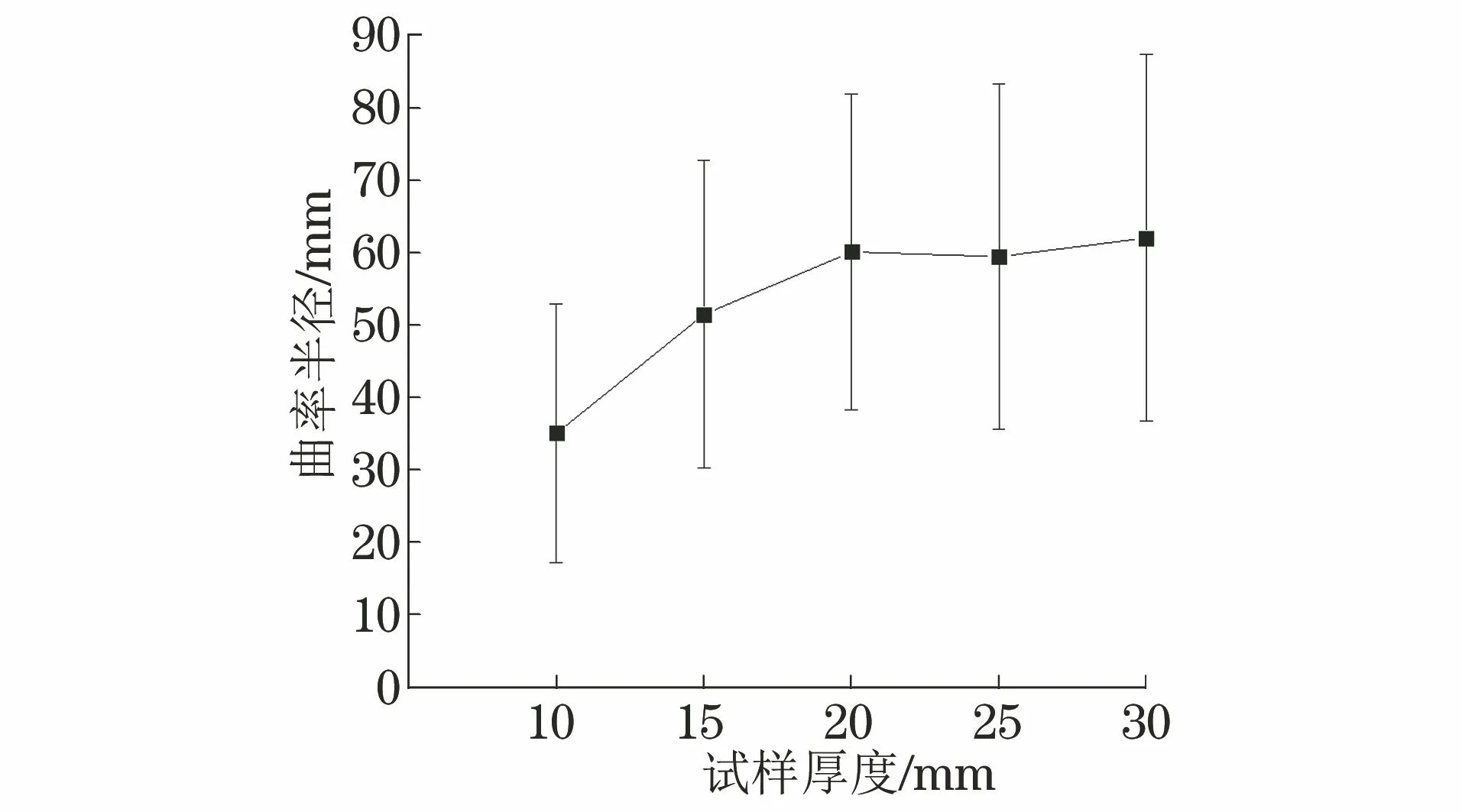
圖7 曲率半徑R隨試樣厚度的變化

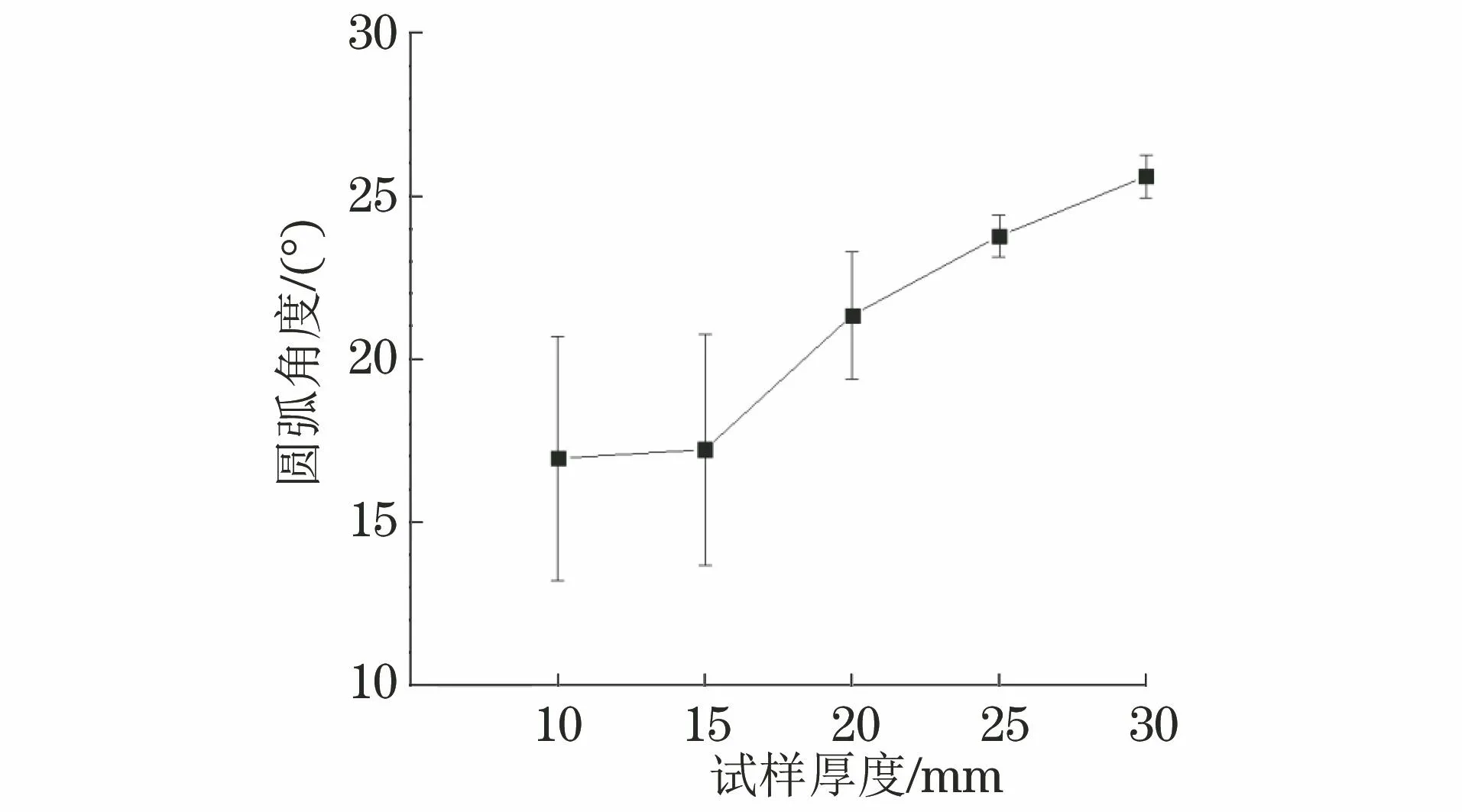
圖8 圓弧角度2α隨試樣厚度的變化

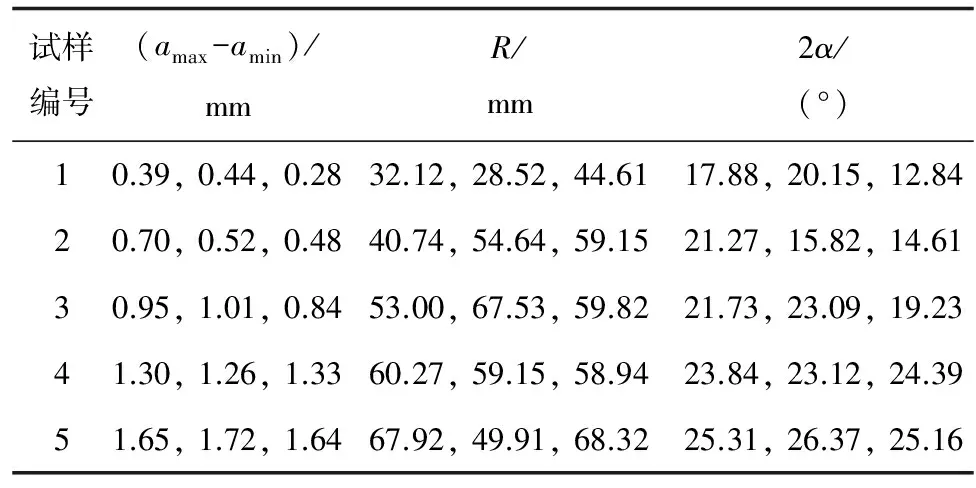
表3 不同厚度試樣的amax-amin值、曲率半徑R和圓弧角度2α計算結果

用有限元方法模擬amax/W=0.4時,不同厚度試樣的受力狀態,圓弧角度2α采用圖8中的平均值。不同厚度試樣對應的歸一化實際裂紋長度a′/W和歸一化柔度法測算裂紋長度a(1)/W對比結果如圖9所示。由圖9可知：a(1)/W比a′/W小,當試樣厚度由25 mm增大至30 mm時,a(1)/W比a′/W差值明顯增大,由約0.5%增大至約2.0%。說明隨著試樣厚度的增加,圓弧角度2α增大,影響了裂紋的平直度,柔度法測算的裂紋長度a(1)比實際裂紋長度a′偏小。對于疲勞裂紋擴展速率試驗,不同材料的裂紋前緣彎曲程度不同,如果材料裂紋前緣的圓弧角度過大,則不宜采用較厚(厚度不小于30 mm)試樣進行試驗。

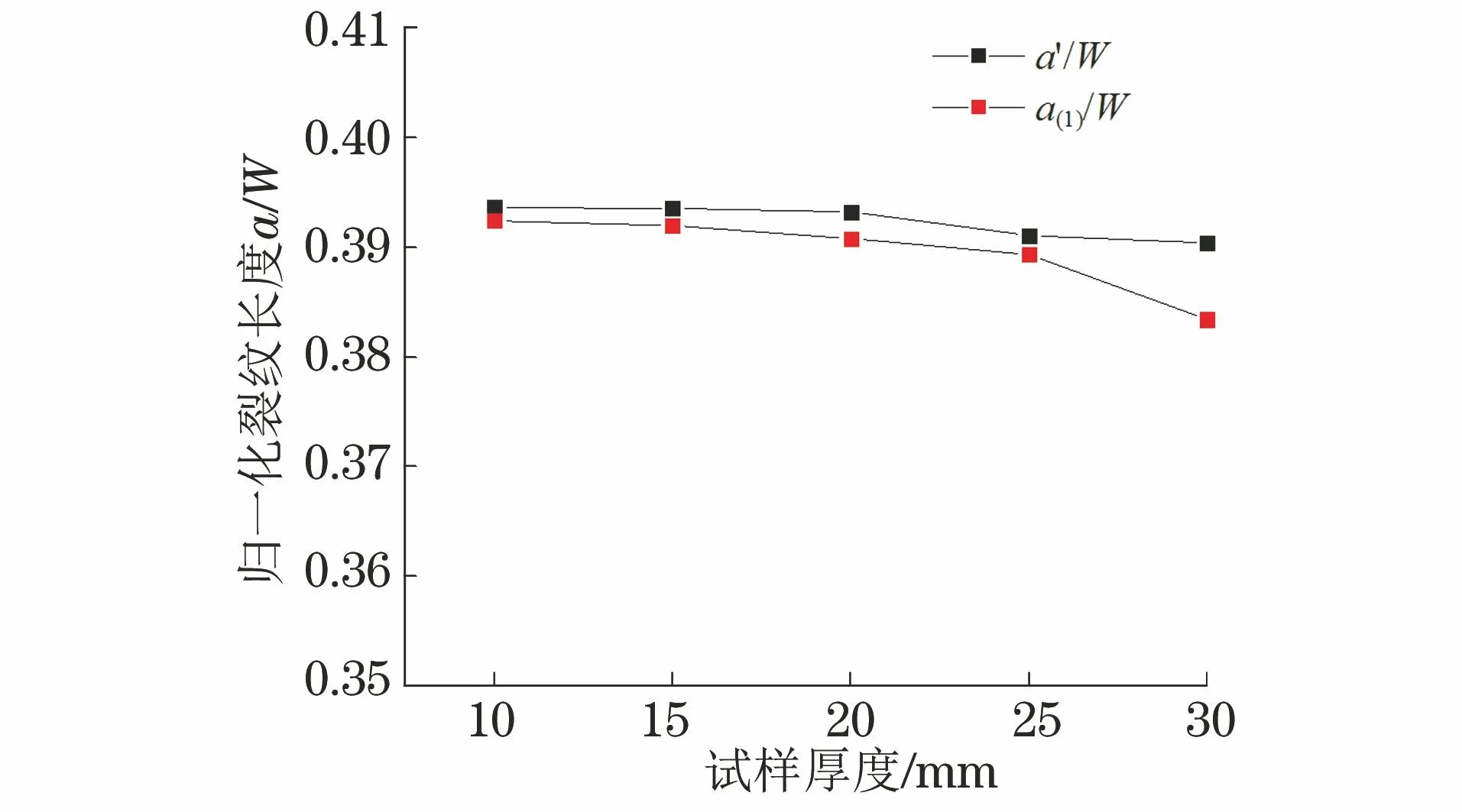
圖9 歸一化裂紋長度隨試樣厚度的變化情況

3.4 引伸計標距對裂紋嘴張開位移的影響

裂紋嘴張開位移V是指試樣邊緣處裂紋面的張開量,實際試驗時由于引伸計標距的原因,引伸計測得的裂紋嘴張開位移V′是實際位移V的近似值。三點彎曲加載時,假設試樣兩側以裂紋頂端為圓心對稱旋轉,以試樣左半部為例,裂紋嘴張開位移V的計算方法如式(8)～(10)所示。

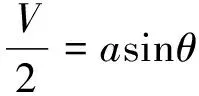
(8)

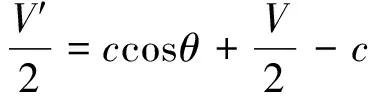
(9)

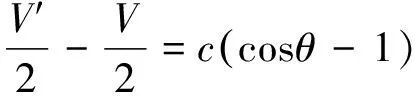
(10)

式中：a為裂紋長度;c為引伸計標距的一半;θ為單側的旋轉角度。

由式(10)可知：引伸計測得的張開位移V′比試樣實際的張開位移V小,根據式(1),a(1)/W與柔度V/F是單調遞增關系,因此由V′/F得到的裂紋長度會存在偏小的情況;在θ一定的情況下,引伸計標距2c越大,V′/F偏小的程度越大。

根據有限元模擬的結果,引伸計標距為10 mm時對應的柔度V′/F與裂紋嘴張開位移的柔度V/F幾乎一致,經過計算,試樣在最大載荷時的θ角很小,絕對值|cosθ-1|<0.000 1。對于疲勞裂紋擴展速率試驗,試樣整體處于彈性狀態,裂紋面的張開量較小(θ值較小),引伸計標距對柔度測量的影響可以忽略。對于某些裂紋面張開量較大(θ值較大)的斷裂試驗,如裂紋尖端張開位移、延性斷裂韌性試驗等,引伸計標距過大,會造成裂紋嘴張開位移V的測量值偏小,進而影響試驗結果。

4 結論

(1) 對于不同厚度的10Ni6CrCuMoV鋼三點彎曲試樣,當試樣厚度不大于25 mm,歸一化實際裂紋長度a′/W≥0.3時,柔度法測算裂紋長度a(1)與真實裂紋長度a′相差小于5%,認為a(1)有較好的準確性。

(2) 當a(3)/W≤0.2時,a(1)/W與a(3)/W相比明顯偏小,a(3)/W=0.15時,a(1)/W與a(3)/W相差約17%;當a(3)/W≥0.3時,a(1)/W與a(3)/W相差小于0.5%。根據柔度函數關系式的適用條件,使用式(1)進行裂紋長度測算時,要求實際裂紋長度a′/W≥0.3,以保證測算結果準確。

(3) 用有限元方法模擬三點彎曲試樣中平直的貫穿型裂紋as,兩柔度函數關系式(1)和式(3)在as/W≥0.3時與模擬結果均有較高符合性,a(1)/W、a(3)/W與as/W相差小于2%;當試樣厚度不大于40 mm時,裂紋中心的平面應變狀態對柔度函數關系沒有明顯影響,在式(1)中使用材料的彈性模量E進行計算,可以獲得較準確的測算裂紋長度。

(4) 用圓弧角度2α來描述裂紋前緣的彎曲程度,根據試驗結果,隨著試樣厚度的增大,2α明顯增大,裂紋平直度降低,導致柔度法測算的裂紋長度a(1)比實際裂紋長度a′偏小。對于疲勞裂紋擴展速率試驗,不同材料的裂紋前緣彎曲程度不同,如果材料裂紋前緣的圓弧角度過大,則不宜采用較厚(厚度不小于30 mm)試樣進行試驗。

(5) 在疲勞裂紋擴展速率試驗過程中,試樣整體處于彈性狀態,裂紋面的張開量很小,引伸計標距對柔度測量的影響可以忽略。對于某些裂紋面張開量較大的斷裂試驗,如裂紋尖端張開位移、延性斷裂韌性試驗等,引伸計標距過大會造成裂紋嘴張開位移V的測量值偏小,影響試驗結果。