采用重組模板的權重優化WENO-Z格式

柴得林,王 強,2,易 賢,2*,劉 宇

(1. 中國空氣動力研究與發展中心 結冰與防除冰重點實驗室, 四川 綿陽 621000;2. 中國空氣動力研究與發展中心 空氣動力學國家重點實驗室, 四川 綿陽 621000)

隨著電子計算機技術的飛速發展,計算流體動力學在流體力學領域的理論研究與工程應用中起到越來越大的作用。作為計算流體動力學的基礎之一,離散格式的性能對流場數值模擬具有重要影響。特別地,加權本質無振蕩(weighted essentially non-oscillatory,WENO)格式的提出極大地推進了含激波等復雜流動結構的流場的精確數值模擬。

Liu等[1]在本質無振蕩(essentially non-oscillatory, ENO)[2-3]格式的基礎上創造性地提出了WENO 格式,采用子模板上的低階格式的非線性凸組合使得格式兼具高精度與本質無振蕩特性,并設計了有限體積形式的3階、4階精度 WENO 格式。Jiang等[4]對 WENO 格式進行理論分析,將WENO格式拓展至有限差分形式,系統地設計了任意階有限差分形式格式的光滑因子與非線性權計算方法,他們提出的 5 階WENO 格式成為最經典的 WENO 格式之一,一般記為WENO-JS格式。

盡管WENO-JS格式具有優越的激波捕捉性能,但仍存在耗散過大,極值點處精度降階等不足。圍繞WENO-JS格式,學者們開展了大量的性能優化研究。在非線性權計算方面,Henrick等[5]指出5階WENO-JS格式在求解雙曲守恒律時并未完全滿足 5 階精度,在極值點附近發生降階。為此,他們在非線性權的計算中引入了一個非線性權映射函數,設計了一種完全滿足 5 階精度的改進WENO格式,記為 WENO-M 格式。根據 WENO-M 格式的思想,多種新型映射函數被提出并應用于 WENO 格式的優化[6-8]。Borges等[9]從增大間斷子模板的權重分配的角度開展研究,指出增大非線性加權時間斷子模板的權重,可降低格式耗散,優化格式性能;在這一理論上,他們設計了一個高階光滑因子,構造了新的非線性權,提出了耗散更低、分辨率更高的 5 階 WENO-Z 格式。

在WENO-Z格式的基礎上,Liu等[10]改進了5階WENO-Z格式的高階光滑因子及其在非線性權中的應用,使得格式既滿足5階精度充分條件,又具有較低耗散。Castro等[11]給出了高階光滑因子的通用公式,將 WENO-Z 格式拓展至任意奇數階。Acker等[12]在WENO-Z格式的非線性權公式中增加了光滑因子比值相關項,提出WENO-Z+格式,進一步提高了格式中間斷子模板的權重,改善了格式對高頻波的分辨率,并指出在通常的應用中,間斷子模板上的權重對WENO格式實際計算性能的影響起主要因素。文獻[13-16]均引入光滑因子比值優化了格式權重, 文獻[17-20]對光滑因子進行了重新設計與構造。徐維錚等[21]則對3階WENO-Z格式的光滑因子進行了多種設計與系統研究,研究表明格式在連續解非極值點處的理論精度對實際計算性能起決定性的作用,極值點處的精度影響則較小。上述研究表明改進非線性權計算方法可有效實現WENO-Z格式耗散降低,性能提升。

與上述僅改進非線性權計算方法的研究不同,模板優化是WENO格式改進的另一重要方法。Martín等[22]和HU等[23]通過在WENO構造模板中引入下迎風模板,優化權重,分別提出了WENO-SYMBO和WENO-CU6格式;Zhu等[24]則創造性地設計了由一個5點模板和兩個2點模板加權得到的5 階有限差分 WENO格式,該格式對線性權的選擇更為靈活,實現更為簡單。這些研究在優化模板的基礎上,對非線性權計算方法,包括線性權的選取、光滑因子的計算等,進行了一定改進,最終實現了格式性能的提升。

盡管上述研究已經實現了WENO格式性能的大幅改善,模板優化方法也往往伴隨著非線性權計算方法的重新設計,但鮮有研究對非線性權計算方法改進與模板優化之間的關系進行研究,鮮有研究提出可以轉化為改進非線性權計算方法的模板優化方法。

本文以5階WENO-Z格式為研究對象,借鑒文獻[22-24]的優化模板思路,在WENO-Z格式構造中引入一個由3點模板重新組合形成的4點模板,取其上重構格式為對應3點模板格式的線性組合,通過這種模板重組方法實現了格式的非線性權調節與性能提升;同時借助子模板的線性組合特性將所提模板優化方法等效轉化為格式的改進非線性權計算方法;采用一系列基準問題對改進格式性能提升進行數值驗證。

1 WENO-Z格式

以一維雙曲守恒律為研究對象

(1)

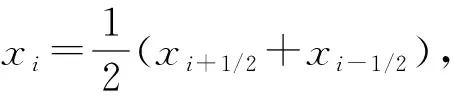
(2)

式中,h(x)為數值通量函數,其隱式定義為

(3)

(4)

5階WENO-JS格式或WENO-Z格式的重構模板如圖1所示。

圖1 5階WENO-JS/WENO-Z格式重構模板Fig.1 Reconstruction stencils of fifth-order WENO-JS/WENO-Z

S(5)={Ii-2,Ii-1,Ii,Ii+1,Ii+2}為構造大模板,可劃分為3個互有重疊的3點子模板,即S0={Ii-2,Ii-1,Ii}、S1={Ii-1,Ii,Ii+1}和S2={Ii,Ii+1,Ii+2}。在各子模板上計算數值通量對應的線性格式,可得

(5)

而大模板上數值通量對應的5階線性格式為

(6)

式中:dm為線性權重,d0=0.1,d1=0.6,d2=0.3;m=0,1,2。引入與其相對應的非線性權ωm,則可得WENO格式的一般形式

(7)

5階WENO-JS格式的非線性權計算公式為

(8)

式中,βm為光滑因子,表征相應模板上變量的光滑程度,ε為一正數小量,防止分母為0。文獻[4]給出的k階WENO格式的光滑因子βm通用計算公式為

(9)

對于5階WENO-JS格式各光滑因子為

(10)

而ε則取經驗值10-6。

5階WENO-Z格式的非線性權計算公式為

(11)

式中:βm為式(10)所示的WENO-JS光滑因子;τ5=|β0-β2|為高階光滑因子;p為度量光滑因子對非線性權的影響的指數,一般取1;εZ為一正數小量,防止分母為0。參考文獻[9],本文εZ取一極小量10-40使其僅起到防止分母為0的作用。較之WENO-JS格式,WENO-Z格式增大了間斷模板的非線性權,降低了格式耗散,提高了格式分辨率。

2 重組模板WENO-Z格式

2.1 模板重組

圖1中WENO-Z格式計算xi+1/2處的值時所用整體模板是上迎風的,為了降低格式耗散,應使得模板更接近中心模板,因而本文在WENO格式的構造中引入中心模板S3={Ii-1,Ii,Ii+1,Ii+2},如圖2所示。則改進格式含有4個子模板,記改進格式為WENO-ZF,F為單純記號,則新模板組合下,對應加權公式為

(12)

2.2 線性權與子模板S3參數計算

由圖2可知子模板S3為S1、S2的組合,假設S3上線性格式為S1、S2對應線性格式的線性組合,即

圖2 5階WENO-ZF格式重構模板Fig.2 Reconstruction stencils of fifth-order WENO-ZF

(13)

(14)

同時有

(15)

由數值通量線性格式精度式(4)得

(16)

(17)

在單元Ii=[xi-1/2,xi+1/2]上采用與式(15)相同的線性組合,則有

將式(18)代入光滑因子的定義式(9)可得S3上光滑因子計算式為

2.3 非線性加權與簡化

參考WENO-Z格式的加權方法,仍將WENO-ZF格式的非線性權取為

(20)

其中:m=0,1,2,3;參考文獻[9],取τ5=|β0-β2|,p=1,εZF=10-40。

(21)

式(21)中,τ5、βm、εZF與WENO-ZF格式中式(20)中的定義及取值相同。對比式(20)和式(21)可知,重組模板的模板優化方案最終等效為非線性權計算方法的優化。為減少計算量,后續數值實驗中采用式(21)進行WENO-ZF格式的計算。

(22)

將其代入式(18)得

(23)

將式(22)、式(23)代入光滑因子的定義式(9),可得

(24)

因而,計算非線性權時可取

(25)

這樣可以減少計算量。為便于表示,下文中式(19)和式(25)計算β3的改進格式分別記為WENO-ZF1、WENO-ZF2。

2.4 近似色散關系分析

近似色散關系(approximate dispersion relation,ADR)分析方法[25]可有效分析非線性格式的譜特性,即色散耗散特性,廣泛應用于非線性格式的設計與優化。采用該方法計算所得WENO-ZF1、WENO-ZF2格式的色散耗散特性如圖3所示。圖中Φ(φ)為波數φ對應的修正波數,其實部和虛部分別反映格式的色散與耗散。

比較圖3中各格式色散與耗散特性:低頻波范圍內,所有格式均有理想的色散耗散;中高頻波范圍內,WENO-ZF1與WENO-ZF2格式的色散與耗散均小于WENO-Z格式,而WENO-JS格式的色散和耗散則明顯大于這三種格式,這表明采用模板重組引入模板S3改進WENO格式的方法可以有效降低格式色散與耗散。對比WENO-ZF1與WENO-ZF2格式的色散與耗散特性,WENO-ZF2格式除對部分中頻波的色散略小于WENO-ZF1格式外,其他情況下對中高頻波的色散和耗散均大于WENO-ZF1格式。

(a) 色散(a) Dispersion

(b) 耗散(b) Dissipation

3 數值實驗

本節采用5階WENO-JS、WENO-Z、WENO-ZF1和WENO-ZF2格式對一系列經典的數值算例進行模擬,以驗證格式的精度及其色散耗散特性、分辨率等方面的性能。需說明的是,算例中變量如無特別說明,均為無量綱量;各算例的時間離散均采用3階TVD Runge-Kutta 格式計算。

3.1 線性對流方程

對線性對流方程

(26)

取初始條件u(x,0)=sin(πx),在網格數為20至320的均勻網格上進行計算,結束時間取t=2,計算所得L1、L∞誤差與精度如表1所示。

由表1中數據可得,四種WENO格式均可達到設計的5階精度;相同網格數下,WENO-Z、WENO-ZF1、WENO-ZF2三種格式誤差較為接近,較WENO-JS格式小一個數量級。比較WENO-Z、WENO-ZF1、WENO-ZF2三種格式誤差,對于L∞誤差,相同網格下,WENO-ZF1格式與WENO-ZF2格式誤差相當,均小于WENO-Z格式。對于L1誤差,相同粗網格下,WENO-ZF1格式與WENO-ZF2格式誤差相當,均小于WENO-Z格式;相同細網格下,三種格式誤差基本相同。綜上,該算例中WENO-ZF1和WENO-ZF2格式可達到設計收斂精度,且有較WENO-Z格式更高的分辨率。

表1 t=2時線性對流方程各WENO格式的誤差與精度

3.2 一維歐拉方程

求解歐拉方程時,為了計算的穩定性,將方程投影至特征空間,對特征變量進行求解,并采用Lax-Friedrichs通量分裂方法對通量進行分裂,采用Roe平均方法計算網格單元界面上的變量。

對一維歐拉方程

(27)

進行計算,式(27)中守恒變量U=[ρ,ρu,ρE]T,通量F=[ρu,ρu2+p,(ρE+p)u]T。

3.2.1 Sod激波管

計算Sod激波管問題,其初始條件為

(28)

左右邊界設置為零梯度邊界條件,取200個均勻網格進行計算,模擬該問題至t=0.4,計算結果密度分布及激波與接觸間斷附近的密度分布放大圖如圖4所示。

(a) 密度分布(a) Density distributions

(b) 接觸間斷附近局部放大圖(b) Locally enlarged plot near the contact discontinuity

(c) 激波附近局部放大圖(c) Locally enlarged plot near the shock

圖4表明各格式均可無振蕩計算得到激波與接觸間斷。但比較圖4(b)和圖4(c)中各格式在接觸間斷與激波附近的結果,WENO-ZF1、WENO-ZF2格式結果接近,略優于WENO-Z格式,而WENO-JS格式抹平較大。這表明,基于模板重組的WENO-ZF1、WENO-ZF2格式耗散低于WENO-Z格式。

3.2.2 激波-密度波相互作用問題

計算激波-密度波相互作用問題,即Shu-Osher問題,該問題的初始條件為

(29)

計算中左右邊界設置為零梯度邊界條件,取200個均勻網格進行計算,模擬該問題至t=1.8。由于該問題無解析解,故將在網格數為2 000的均勻網格上采用WENO-JS格式計算所得結果作為基準解。圖5為網格數為200時各格式計算結果的密度分布。

圖5中各格式對鋸齒狀的聲波形成的一系列小激波及x=2.4附近的激波都有較好的捕捉效果,但對高頻振蕩的折射熵波計算效果較差。對比激波附近放大圖,就所得激波陡峭程度而言,WENO-ZF1、WENO-ZF2格式結果接近,優于WENO-Z格式,且優于WENO-JS格式。對比折射熵波附近放大圖,在對幅值的計算上,WENO-ZF2結果接近甚至優于WENO-ZF1格式,兩者均優于WENO-Z格式,WENO-JS格式則最差。可見,改進格式的色散耗散特性得到了優化。

(a) 密度分布(a) Density distributions

(b) 圖(a)局部放大圖(b) Locally enlarged plot of graph (a)

3.3 二維歐拉方程

對二維歐拉方程

(30)

做計算,式(30)中守恒變量U=[ρ,ρu,ρv,ρE]T,各方向通量F=[ρu,ρu2+p,ρuv,(ρE+p)u]T,G=[ρv,ρuv,ρv2+p,(ρE+p)v]T。特征投影、Lax-Friedrichs通量分裂等處理方法與求解一維歐拉方程相同。

3.3.1 二維黎曼問題

該問題中取計算區域為[0,1]×[0,1],初場為

(31)

計算區域劃分為400×400的均勻網格,各邊界均采用零梯度邊界條件,計算至t=0.8。計算結果中含一道射流和四道激波等復雜結構,可以有效校驗數值格式的色散耗散特性和激波捕捉特性。各格式計算結果密度分布如圖6所示,圖中展示0.14到 1.70均勻分布的40條密度等值線。

由圖6可得,四種WENO格式計算結果均可正確反映流場分布,實現對激波的有效捕捉。但對比滑移線附近的流場,在對復雜離散渦的計算上,WENO-ZF1和WENO-ZF2格式計算得到了更多細節結構,WENO-Z格式次之,WENO-JS更次之。這表明,四種格式中,WENO-ZF1與WENO-ZF2格式耗散最小,WENO-Z格式次之,WENO-JS格式耗散最大。

(a) WENO-JS

(b) WENO-Z

(c) WENO-ZF1

(d) WENO-ZF2

3.3.2 激波-渦相互作用

激波-渦相互作用問題描述二維空間下運動的渦穿過靜止的馬赫數為1.1的激波時,二者相互作用的問題。計算區域為[0,2]×[0,1]。初始條件為:在x=0.5處給定一道垂直于x軸的靜止的激波,激波左側物理量為

(32)

激波右側物理量由Rankine-Hugoniot條件計算得出。同時,激波左側疊加一個以(0.25,0.5)為中心的渦,即在激波左側速度、溫度和熵給定值上施加渦對應的脈動量,各脈動量為

(33)

(a) WENO-ZF1

(b) WENO-ZF2

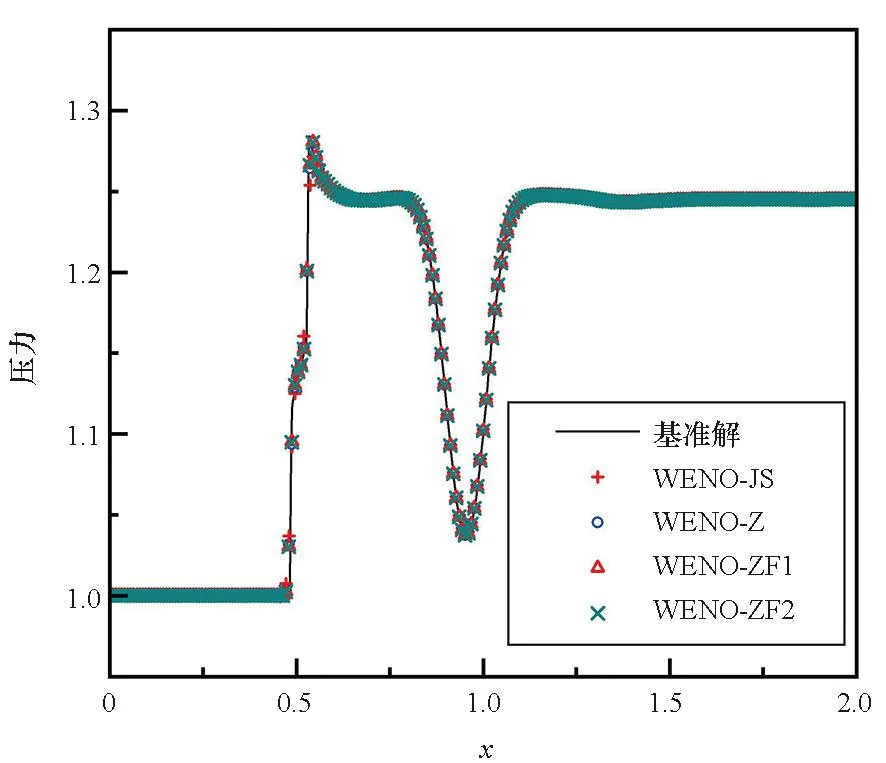
圖8 t=0.6時激波-渦相互作用y=0.5壓力分布Fig.8 Pressure distributions of the shock-vortex interaction problem on central line y=0.5 at t=0.6

圖7與圖8中計算結果表明WENO-ZF1、WENO-ZF2格式均可較好地模擬這一問題,得到基本的流場分布,得到正確的激波結構和渦核處的低壓區。比較圖9中激波附近和渦核附近的壓力分布局部放大圖,在對激波的捕捉和渦核壓力的計算上,WENO-ZF1格式與WENO-ZF2格式計算結果相當,優于WENO-Z格式,WENO-JS格式計算結果的偏差最大。綜上,改進的WENO-ZF1格式、WENO-ZF2格式對激波的捕捉特性和小尺度流場結構的分辨率均優于WENO-Z格式與WENO-JS格式。

(a) 激波附近壓力分布(a) Pressure distributions near the shock wave

(b) 渦核附近壓力分布(b) Pressure distributions near the vortex core

表2給出采用不同WENO格式計算上述算例中線性對流方程(初始分布為正弦波,網格數為320)、二維黎曼問題、激波-渦相互作用問題的相對用時,其他算例由于耗時較短,難以精確統計,未予列出。表2中分別以各算例對應WENO-Z格式所用時間作為單位時間對其他格式所用時間進行無量綱化,其中WENO-ZF格式表示采用最初的4個子模板加權公式計算的WENO-ZF格式(該格式與WENO-ZF1格式完全等價,計算結果完全相同,故在各算例結果中沒有列出)。由表中數據可得,最初的WENO-ZF格式較WENO-Z格式用時長7%～19%,WENO-ZF1格式較WENO-Z格式用時長4%～16%,WENO-ZF2格式較WENO-Z格式用時長1%～4%。可見,WENO-ZF1格式的等效轉化較WENO-ZF格式提高了格式效率,WENO-ZF2格式的β3計算簡化則進一步提高了格式效率。

表2 計算不同算例時各WENO格式所用相對時間

4 結論

本文在5階有限差分WENO-Z格式的基礎上,提出一種模板重組技術:將原格式中的子模板組合得到一中心子模板S3,S3上逼近函數取對應原始子模板的線性組合;在包括S3的4個子模板上采用WENO-Z格式加權方法得到WENO-ZF格式。通過數學運算將WENO-ZF格式轉換為原始子模板上的改進非線性權計算方法的WENO-ZF1格式。WENO-ZF和WENO-ZF1格式的構建首次實現了格式模板優化與非線性權改進二者的等價轉換。

為簡化計算,提高格式效率,本文又將WENO-ZF1中S3上光滑因子β3簡化為原始子模板光滑因子的線性組合,得到了計算更為簡潔的WENO-ZF2格式。

ADR分析表明,WENO-ZF1格式和WENO-ZF2格式色散耗散特性得到不同程度的優化。數值實驗表明,WENO-ZF1格式和WENO-ZF2格式可達到理想的設計精度;較WENO-Z格式、WENO-JS格式,具有更低的耗散,對激波有更優的捕捉特性,對小尺度流場結構有更高的分辨率。格式效率上,WENO-ZF2格式效率高于WENO-ZF1格式,又高于采用4個子模板加權公式計算的最初WENO-ZF格式。