基于深度學習的鈍體斷面外形氣動性能高效預測方法

李少鵬,李海,李珂

（重慶大學 土木工程學院，重慶 400045）

平均風產生的靜荷載簡稱靜力風荷載，通常由無量綱參數三分力系數來描述，而過大的阻力和升力矩會讓鈍體斷面產生橫向位移和扭轉，嚴重時甚至會出現風致靜力失穩，進而影響結構的安全性和穩定性，由此可見，三分力系數對鈍體斷面抗風設計至關重要[1-3]。三分力系數影響因素有鈍體斷面氣動外形、風攻角、雷諾數等，其中鈍體斷面氣動外形尤為重要，不同鈍體斷面的截面形式、高寬比不同，則對應的三分力系數及變化規律也不盡相同[4-6]，這也導致目前學術界仍未建立起鈍體斷面氣動外形和三分力系數之間的數學聯系。

目前測定三分力系數的常用方法主要有兩種，1）將節段模型放入風洞進行試驗，得到三分力系數[7-8]；2）采用計算流體力學(CFD)仿真計算，得到三分力系數[9-10]。雖然這兩種方法都廣泛應用，但各有缺點，風洞試驗設備投資大、試驗所需人力物力較多，CFD 仿真計算則需要消耗大量計算資源，為了保證兩者試驗數據的準確性，可能都需要數周才能獲得三分力系數。因此，算出靜力風荷載后,精細地預測結構各組成部分所受到的風荷載需更長時間，大大制約了結構抗風設計效率。

近年來，隨著神經網絡技術的不斷發展，人工智能預測技術逐漸應用在抗風領域[11]。針對鈍體斷面，李喬等[12]采用BP 神經網絡預測主梁斷面靜力三分力系數；楊興旺[13]采用BP 網絡識別橋梁主梁顫振臨界風速、靜力三分力系數；黃繼鴻等[14]采用BP 神經網絡預測翼型的升力系數和阻力系數；針對扁平箱梁和倒梯形箱梁兩種斷面的氣動參數，陳訥郁等[15]采用BP 神經網絡進行預測；Liao 等[16]通過4 種機器學習方法的對比，精準預測不同流線型箱梁的顫振臨界風速；Hu 等[17-18]通過多種機器學習方法的對比，精準預測圓柱表面風壓和壓力系數。以上研究雖然提供了對鈍體斷面新的表達方法，但對于氣動外形，僅用參數化和坐標表達具有一定的局限性，復雜斷面難以快速進行，不具備普適性。Chen等[19]提出采用0-1 數據對表示氣動外形，0 表示氣動外形外，1 表示氣動外形內，但這種氣動外形設計無法提供足夠的信息；Miyanawala 等[20]提出用Euler 距離場表達氣動外形，快速高效、具有足夠信息。考慮直接預測三分力系數較為復雜，對模型性能要求較高，因此，采用深度學習方法搭建模型。在預測流線型斷面的三分力系數和壓力方面，深度學習方法也有一定應用，陳海等[21]搭建深度學習模型——卷積神經網絡，預測了翼型的法向力系數；廖鵬等[22]等利用深度學習模型，結合CFD 預測翼型前緣壓力分布。然而，目前采用深度學習方法預測未知鈍體斷面三分力系數的研究還較少。

深度學習是人工智能領域近年來取得的最重大的研究成果之一，由于出色的數據擬合能力、GPU 等硬件的出現，其進入高速發展階段。卷積神經網絡（CNN）可以對圖像特征進行自動識別，且卷積核平移不變性，可以極大地降低訓練難度，非常適合處理不同形狀鈍體斷面圖像[22]。筆者提出，鈍體斷面氣動外形以圖像數據作為輸入，可以實現不同鈍體斷面外形的一致表達，有效回避異構數據問題。該方法通過CNN 深度學習模型預測鈍體斷面三分力系數，將鈍體斷面氣動外形與三分力系數直接關聯，解決傳統方法獲取三分力系數效率低的問題，為今后氣動外形優化提供技術支持。

1 鈍體斷面氣動系數預測模型

深度學習中的神經網絡模型輸入需能夠表達鈍體斷面的氣動外形信息，且該信息應該具有一致的表達結構。對于鈍體斷面氣動外形的表達問題，使用坐標點的傳統方式會使輸入數據的結構和大小與外形相關聯，引發數據異構問題。針對該問題，提出一種圖像形式的氣動外形描述方法，可以有效地與卷積神經網絡結合，實現輸入數據一致性表達的同時，提高了信息傳遞效率。基于此方法，以3 個場對氣動外形進行描述，分別是距離場、順風向坐標場和橫風向坐標場。

1.1 距離場

外形影響氣動力的最主要因素之一是流場的邊界層。采用距離場的形式描述外形，將外形以周圍空間各點與外形的距離進行表達，可以強化輸入信息與邊界層的邏輯聯系。具體表達如式（1）所示。

式中：指數函數內部表示流場空間位置RΦ與氣動外形最近邊界RΓ之間的無量綱距離；B為氣動外形特征長度；U為平均風速，m/s。因為更加關注靠近氣動外形邊界周圍的流場，忽略了離氣動外形較遠的流場，需要輸入更多的邊界周圍信息，為此，通過負指數形式來增加邊界層附近的權重。采樣位置在邊界上或者邊界內時，β為0，反之為1。

圖1 為距離場，其中，紅色越深，表示該坐標點數值越接近于1，即該坐標點越接近于氣動外形邊界，藍色越深，表示該坐標點數值越接近于0，即該坐標點離氣動外形邊界越遠。

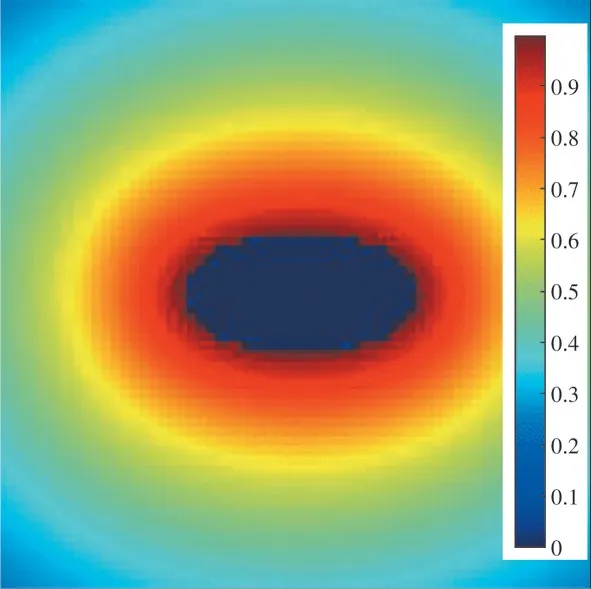
圖1 距離場Fig.1 Distance field

1.2 順風向坐標場和橫風向坐標場

單純采用距離場作為輸入存在信息缺失的問題，為了方便描述，考慮如圖2 所示的鋸齒狀形狀。對于卷積神經網絡，其感受野為圖像的某一區域，以圖中紅線框表示。當感受野平動時，如果僅使用距離場信息，氣動外形不同位置會提供相同的數據信息，導致卷積神經網絡接受到相同的輸入特征信息。然而，實際情況是氣動外形不同位置對應的壓力場不同，對阻力系數的貢獻也不盡相同。因此，需要構造其他輸入信息，以確保信息的充分性。

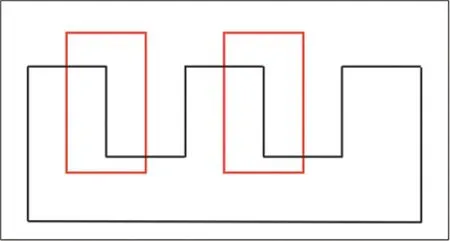
圖2 氣動外形示意圖Fig.2 Schematic diagram of aerodynamic shape

為兼顧輸入信息獲取的便攜性和流場信息的必要性，設置一個流場流動方向的圖像數據和一個描述橫風向方向的圖像數據作為輸入數據，即順風向坐標場和橫風向坐標場。

其中，順風向坐標場見式（2），靠近入口的位置為上游，對應的數據較小，靠近出口的位置為下游，對應的數據較大，以此實現對空間上下游的描述。為避免對所有數據再次歸一化，選擇設定最大值為1。

式中：X為空間點的X方向坐標，原點為形狀在順風向投影的中心；采樣位置在邊界上或者邊界內時，β為0，反之為1。圖3 為順風向坐標場，其中，紅色越深，表示該坐標點數值越接近于1，即該坐標點越靠近下游，藍色越深，表示該坐標點數值越接近于0，即該坐標點越靠近上游。

圖3 順風向坐標場Fig.3 Coordinate field of streamwise wind

此外，橫風向坐標場見式（3）。構造方法與順風向坐標場類似，取迎風頂點的橫風向投影中點作為原點。如此，對于圓形、六邊形斷面，原點位于迎風端點；對于零度風攻角的矩形斷面，原點位于迎風面中點。

式中：Y為空間點的Y方向坐標；采樣位置在邊界上或者邊界內時，β為0，反之為1。圖4 為橫風向坐標場，其中，紅色越深，表示該坐標點數值越接近于1，即該坐標點越接近于迎風面中點，藍色越深，表示該坐標點數值越接近于0，即該坐標點離迎風面中點越遠。

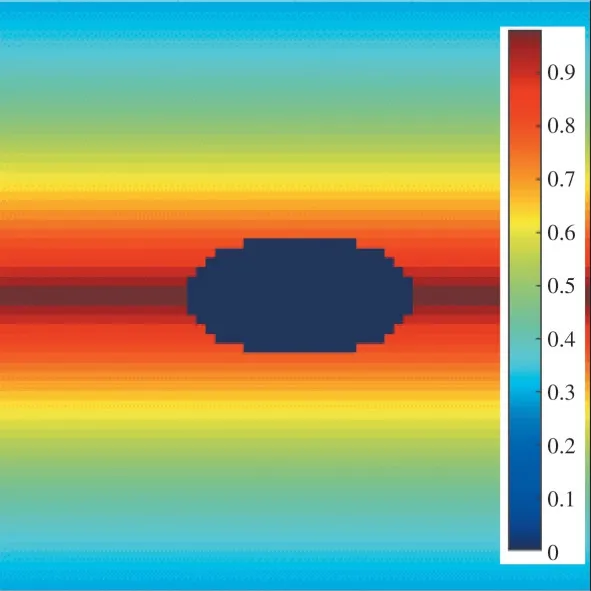
圖4 橫風向坐標場Fig.4 Cross-wind direction coordinate field

2 CNN 框架

輸入為3 個圖像，按照式（1）～式（3）編程，生成距離場、順風向坐標場和橫風向坐標場，輸出為阻力系數。根據輸入和輸出設計構建的CNN 結構如圖5 所示。

圖5 設計的CNN 結構圖Fig.5 Design of CNN structure diagram

輸入層為包含距離信息和流場信息的圖像。輸入圖像分辨率越高，模型預測越準確，但模型復雜度和訓練時間也會增加，因此，選擇合適分辨率非常重要。一般輸入層大小需要能夠被2 整除多次，以保證卷積層深度。選擇64×64 像素為輸入分辨率，有3 個場作為輸入，即64×64×3 的三維矩陣，每個場取值均確保在0 到1 之間。輸出層輸出數據用作回歸分析，對鈍體斷面阻力系數進行預測，為保證輸出數據范圍在0 到1 之間，還加入了sigmoid 函數，見式（4）。

隱藏層中：卷積層是卷積神經網絡的核心模塊，主要確定卷積核尺寸、數量、步長、零填充的數量，卷積核尺寸有越來越小的趨勢，因為小尺寸卷積核可以通過堆疊替代大尺寸卷積層并且感受野大小不變[23]。選擇卷積核大小為3×3，卷積核數量逐步增加。池化層負責對數據空間進行下采樣，其感受野不宜過大，否則易造成池化過于激烈，信息丟失過多，導致欠擬合風險[24]。采用2×2 的感受野做最大池化，滑動步長為2。激活函數選擇ReLU函數，其簡化了計算過程，避免了梯度爆炸和梯度消失問題[25]。全連接層神經元與前一層所有的神經元全部連接，因此，第1 層全連接層神經元數量為S個，第2 層全連接層數量為250 個，第3 層全連接層數量為10 個。

3 輸入和輸出數據獲取

CNN 框架搭建完成后，輸入和輸出數據的獲取也非常關鍵，輸入數據為3 個類圖片的數據場，輸出數據為阻力系數，獲取不同鈍體斷面氣動外形下的輸入和輸出數據，為深度學習模型提供數據支持非常重要。

按照基本形狀，分為正六邊形、圓形、矩形、正菱形4 種，為降低模型訓練難度，所有形狀做到上下和左右對稱。根據橫向長度與豎向長度比值的不同，每種基本形狀下又有不同形狀，為方便起見，采用無量綱形式來確定形狀，固定所有形狀的橫向長度為1。考慮到正六邊形非常接近鈍體斷面，因此，正六邊形輸入數據占到總數據的57%，增強了模型對鈍體斷面的學習能力。

根據正六邊形上下角點距離X=0 直線垂直距離的不同，分成4 組，圓形、矩形、正菱形各1 組，共7組，每組15 個不同形狀，共105 個，如表1 所示。

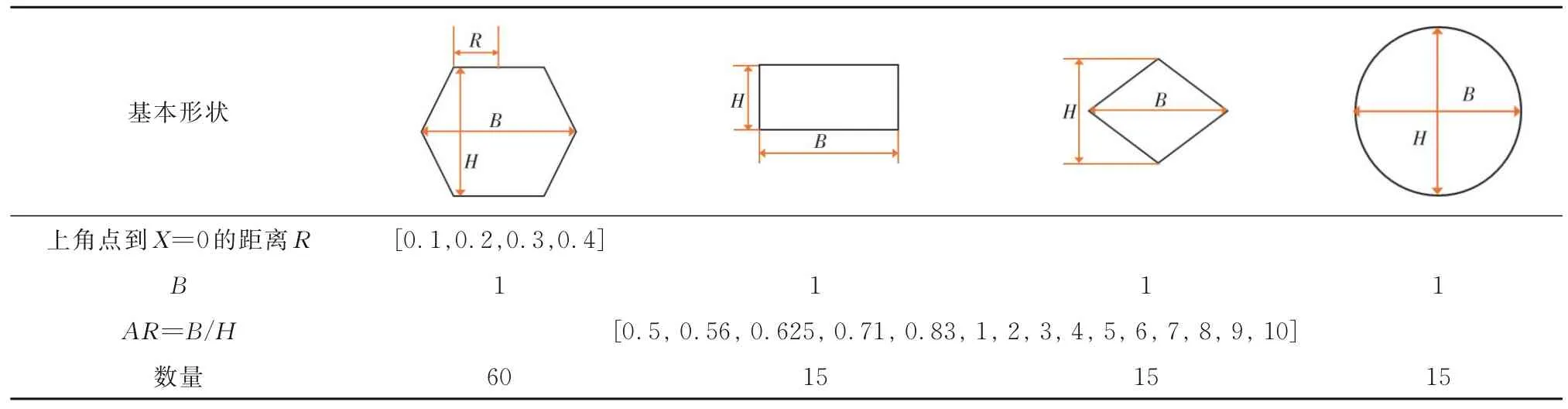
表1 氣動外形工況一覽表Table 1 List of pneumatic shape working conditions

輸入數據獲取需先生成64×64 的網格位置坐標，再根據式（1）～式（3），分別獲得相應網格點到形狀邊界的最小距離信息、流動方向的流場信息和橫風向方向的流場信息。根據流場特征，氣動外形內無流場信息，因此，輸入中氣動外形內的數據信息也人為設置為0。輸入圖像設計的公式中已經考慮歸一化的問題，輸入數據數值都在0 到1 之間。

輸出數據為阻力系數，采用CFD 數值模擬計算得到穩定后的壓力流場。計算域為矩形，長度和寬度分別為15B和10B，B為鈍體截面寬度。為了防止網格變化速度太快，設置3 個計算區域，定義剛性區域，以保持網格形狀不變，在剛性區外使用變形區，實現網格平滑處理，最后，使用固定區域對計算域中的其他部分進行網格劃分。

采用Fluent 軟件，湍流模型選擇RANs 模型，具體選擇k-ωSST 模型，在近壁面采用k-ω模型，邊界層外緣和自由剪切層采用k-ε模型，在k-ω模型和k-ε模型間采用一個混合函數過渡。入口邊界設置為速度入口，出口設置為壓力出口，形狀表面采用無滑移條件，這意味著物理表面的流動狀態等于形狀的運動。待流場穩定后，讀取數據，通過對穩定壓力流場進行數據處理，得到阻力系數。

將全部105 個不同形狀按照上述操作進行處理，得到對應形狀的輸入和輸出數據。綜上所述，輸入數據的圖像張量為(84,3,64,64)，輸出數據張量為(21,3)，快速得到輸入和輸出數據，為之后的模型訓練做好準備。

4 模型性能評測與優化

深度學習模型的深度和寬度直接影響模型性能，模型加深能一定程度提升模型性能，但網絡深度也不是越深越好，深層網絡容易帶來梯度不穩定、網絡退化等問題，且無法通過優化消除，導致模型網絡深度不斷加深，性能并未出現明顯提升，甚至出現下降的情況，模型寬度同理，隨著模型寬度的加深，模型性能并不一定顯著提升。基于之前設計的卷積神經網絡，尋找最優的模型深度與寬度，主要通過模型預測阻力系數的平均絕對誤差MAE，見式（5），結合模型參數量大小綜合判定。

式中：ti為阻力系數真實值；yi為阻力系數預測值。

4.1 模型深度優化

與模型寬度相比，模型深度對于模型性能的影響更大，因此，先確定最優的模型深度[26-27]。主要從模型預測誤差大小和模型參數量來進行評估。將卷積層、池化層、ReLU 層三者稱作一層，選擇卷積神經網絡卷積層數為6、5、4、3、2 的5 類不同層數的CNN 模型來測試不同深度下模型的性能，采用完全相同數據處理后的輸入和輸出數據，模型參數配置完全相同，結果見表2。

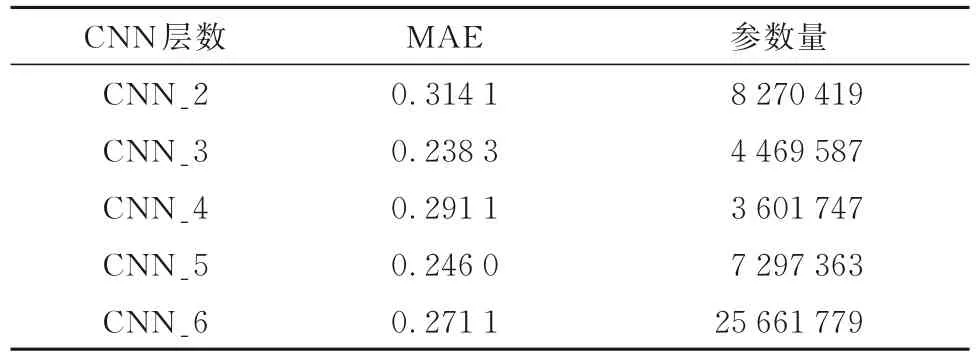
表2 模型深度性能對比Table 2 Comparison of model depth performance

由表2 可知，隨著CNN 層數的增加，MAE 呈先減小到最小值，后出現增大的情況，CNN 層數為5層時，MAE 再次減小，但未減小到CNN 層數為3 層時的MAE，同時，相比于其他CNN 模型，其參數量也相對較少，時間性能更加優秀。CNN 層數為3 層時，MAE 最小，說明該網絡深度下模型性能更優，因此，選擇CNN 層數為3 層的網絡模型。

4.2 模型寬度優化

在確定深度學習模型層數為3 層的情況下，優化深度學習模型寬度D，主要從模型預測誤差大小和模型參數量來進行評估。基于CNN 采樣，第1 層寬度為64，選擇對比的CNN 網絡第1 層寬度分別為128 和256，第2 層和第3 層模型寬度分別為前一層模型寬度的2 倍，采用完全相同數據處理后的輸入和輸出數據，模型參數配置完全相同，結果見表3。

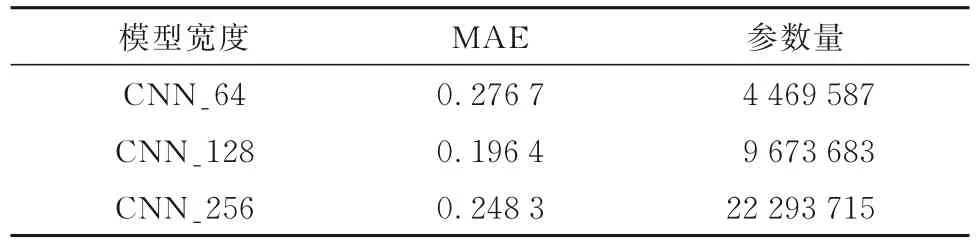
表3 模型寬度性能對比Table 3 Comparison of model width performance

由表3 可知，隨著CNN 寬度的增加，MAE 出現先減小后增大的情況，當CNN 網絡初始寬度D為128 時，MAE 最小，說明該網絡寬度下模型性能更優，同時，其參數量最小，說明本模型消耗時間最少。因此，選擇CNN 網絡初始寬度D為128。

綜上所述，通過MAE 大小和模型參數量大小對比，選擇CNN 層數為3 層的網絡深度，網絡寬度為128-256-512 的網絡模型，第1 層全連接層中神經元數量S為32 768 個。

5 試驗結果

5.1 試驗設置

Pytorch 在科學研究方面表現非常優秀，主要體現在Pytorch 風格非常Python 化，降低了入門的難度，且搭建深度學習模型時可以逐層搭建，方便實時修改。鑒于搭建模型時修改細節比較多，因此，使用Pytorch 來搭建深度學習模型[28]。

在所使用的105 個數據中選取80%作為訓練數據集，剩下的作為驗證數據集，訓練數據集共有84 個不同形狀的輸入和輸出，驗證數據集有21 個不同形狀的輸入和輸出，每次訓練前都對樣本數據進行隨機打亂和批量讀取。模型訓練方法選擇SGD，使用0.2 作為訓練模型的Dropout 率，以防止過擬合。

5.2 預測回歸結果

通過卷積神經網絡預測阻力系數的結果如圖6所示，識別誤差見表4。

表4 阻力系數誤差Table 4 Drag coefficient error

圖6 阻力系數預測結果Fig 6 Drag coefficient prediction results

由圖6 和表4 給出的預測結果可知，當R=0.1、R=0.4 時，正六邊形、矩形和正菱形預測的阻力系數相對誤差較大。當R=0.2、R=0.3 時，正六邊形和圓形預測的阻力系數相對誤差較小，主要是因為當橫向長度與豎向長度的比值(AR)較小時，阻力系數較大，在模型中占的權重較大，導致模型更偏向于擬合權重較大的數據。對于擬合橫向長度與豎向長度的比值(AR)較大、阻力系數較小的情況，無法達到精度要求，使得相對誤差較大。當R=0.2、R=0.3 時，正六邊形和圓形相對誤差較小，明顯可以看到，橫向長度與豎向長度的比值(AR)較大時，擬合非常準確。

深度學習模型針對2 個截面預測的平均相對誤差在10%以下，針對3 個截面預測的平均相對誤差在30%以上，主要是模型輸入和輸出的邏輯關系過于薄弱，導致模型性能容易出現反復。

5.3 模型的時間性能

提出使用卷積神經網絡來預測阻力系數是為了減少得到鈍體斷面氣動性能的時間，因此，有必要評估深度學習方法的時間性能。

通過編寫好的代碼，輸入設計約1 s 即可完成，輸出設計需要進行網格劃分、服務器計算等一系列操作，得到穩定流場后，計算得到阻力系數約需10 s。本文卷積神經網絡進行一次迭代訓練的平均時間為1.08 s，進行1 000 次訓練迭代所需的總時間約為1 080 s，使用已經訓練好的模型進行一次回歸預測，即產生阻力系數所需的平均時間為1 s，一共需要1 092 s。

相比于傳統基于CFD 計算和風洞試驗需要幾周時間才能得到三分力系數，基于深度學習的預測方法在時間性能上得到了數量級的提升。

6 結論

提出將不同鈍體斷面的氣動外形信息轉化為圖像數據而不依賴于傳統設計參數，使用修改和優化后的卷積神經網絡對氣動外形圖像進行回歸預測，建立鈍體斷面氣動外形和阻力系數之間的聯系，且預測精度相對較高。針對相對誤差較大的鈍體斷面，后續將嘗試采用新的輸出，強化輸入和輸出邏輯關系的同時，針對深度學習模型來進行改善，進一步提升阻力系數的預測精度。

與傳統的風洞試驗和CFD 仿真計算方法相比，在允許誤差范圍內，提出的卷積神經網絡模型計算時間達到了數量級的提升，為鈍體斷面氣動外形優化提供了計算基礎。