相協樣本下概率密度函數的調整經驗似然推斷

王寧寧,秦永松

(廣西師范大學數學與統計學院,廣西 桂林 541006)

1.引言

經驗似然是Owen[1-2]在獨立樣本下提出的一種非參數統計推斷方法,與經典方法(如正態逼近理論)以及當前比較流行的統計方法(如Bootstrap)相比,經驗似然方法具有諸如: 置信域的形狀由數據決定、置信域具有Bartlett可修正性、無需構造樞軸量、具有保值域性和函數變換不變性等優點.正因為如此,許多統計學家將這一方法應用到各種統計模型及各種領域.如線性回歸模型的統計推斷[3-4],分位數統計推斷[5]、廣義線性統計推斷[6]等,此外CHEN[7]將經驗似然方法與核方法結合構造精度更高的概率密度函數的置信區間等.然而,上述文獻所提到的經驗似然方法都針對于獨立樣本情形,而現實中相協樣本情形經常出現,針對于相協樣本,現有的研究較多采用分塊經驗似然方法進行推導.Kitamural[8]在α-混合樣本下首次運用分塊經驗似然方法構建參數的置信區間.此后,ZHANG[9]將分塊經驗似然用于構造負相協樣本下非參數整體均值的置信區間、LEI和QIN[10]將分塊經驗似然用于構造負相協樣本下總體分位數的置信區間、QIN等[11]將分塊經驗似然用于構造負相協樣本下概率密度函數的置信區間等.

為了保證經驗似然統計量的存在,需要假定0在數據的凸包內,針對0向量可能不在數據的凸包內的問題,CHEN等[12]提出了調整經驗似然.此后CHEN和HUANG[13]使用調整經驗似然構造總體均值的置信區間并研究了其有限樣本下的性質,ZHOU和JING[14]使用調整經驗似然構造分位數的置信區間等.本文受到文[12,15]的啟發,研究相協樣本[16]下概率密度函數的調整經驗似然推斷問題,采用不分塊的調整經驗似然方法進行推導避免了分塊技術的復雜性,并構造了相協樣本下概率密度函數的調整經驗似然置信區間.通過模擬得到,調整經驗似然(AEL)的表現略優于經驗似然(EL) 和正態逼近(NA).

本文結構如下: 第2節將給出本文的主要結論,第3節將給出有限樣本下的模擬結果,第4節將給出相關的引理及其證明,第5節將給出主要結論的證明.

2.主要結論

設X1,X2,···,Xn是來自總體X的一組嚴平穩相協樣本,f(x)為X的概率密度函數,給定x ∈R,f(x)的核密度估計為

通過拉格朗日乘數法可以得到pi=1/[(n+1)(1+λgn,i(θ))],其中λ=λ(θ)滿足

則對數調整經驗似然比統計量為

下面我們列出一些正則條件,這些正則條件將會用在后面的定理中.通常設C為正常數,在不同情況下可能取到不同的數值.

正則條件:(A1)(i)X1,···,Xn為嚴平穩相協序列(正相協或者負相協);

(A3) 設pn,qn為正整數且滿足:pn+qn ≤n,kn=[n/(pn+qn)],其中[t]表示t的整數部分.設hn>0為窗寬,且pn,qn和hn分別滿足

注2.1本文中條件(A1)-(A3)與文[16]中條件(A1)-(A3)完全相同.條件(A1)(v),(A2)(iii),(A3)(iv)與文[16]推論2.1中條件(b)相同.若f在x的鄰域內有連續的一階導函數,可用文[16]中的條件(a)代替(A1)(v),(A2)(iii),(A3)(iv).

本文主要結論為以下內容.

定理2.1設條件(A1)-(A3)成立且an=o(n),則當n →∞時有

注2.4定理2.1用于構造f(x)的調整經驗似然置信區間.令Zα滿足P(≥Zα)=α,其中0<α<1,則f(x)基于(1-α)的調整經驗似然的置信區間為

為了進一步研究當θf(x)時,對數調整經驗似然比統計量W?(θ)和對數經驗似然比統計量W(θ)的功效,我們引入定理2.2.

定理2.2假設定理2.1的條件(A1)-(A3)成立且an=o(n2/3),對于θf(x),當n →∞時,依概率趨于1有-2(nh)-1/3W?(θ)→∞且-2(nh)-1/3W(θ)→∞成立.

注2.5定理2.2表明,當θf(x)時,對數調整經驗似然比統計量W?(θ)和對數經驗似然比統計量W(θ)以至少(nh)1/3的速率趨于無窮大.

3.模擬結果

本節通過模擬來研究式(2.2)所示的AEL置信區間在有限樣本下的表現.用AELCI表示式(2.2)所示的AEL置信區間,ELCI表示文[15]中式(2.7)所示的EL置信區間,NACI表示式(3.1)中所示的NA置信區間,即

Ⅰ 負相協樣本

i) 多元正態分布隨機樣本

在本節模擬中,(X1,···,Xn)是多元正態隨機向量,且滿足E(X1,···,Xn)=(1,···,1),Cov(Xi,Xj)=-4-(j-i)-1(1≤i ≤n,j>i)和V ar(Xi)=0.52(1≤i ≤n),取an=1,由此生成的{Xi;1≤i ≤n}是負相協序列(見文[17]),該情形下的模擬結果見表1.

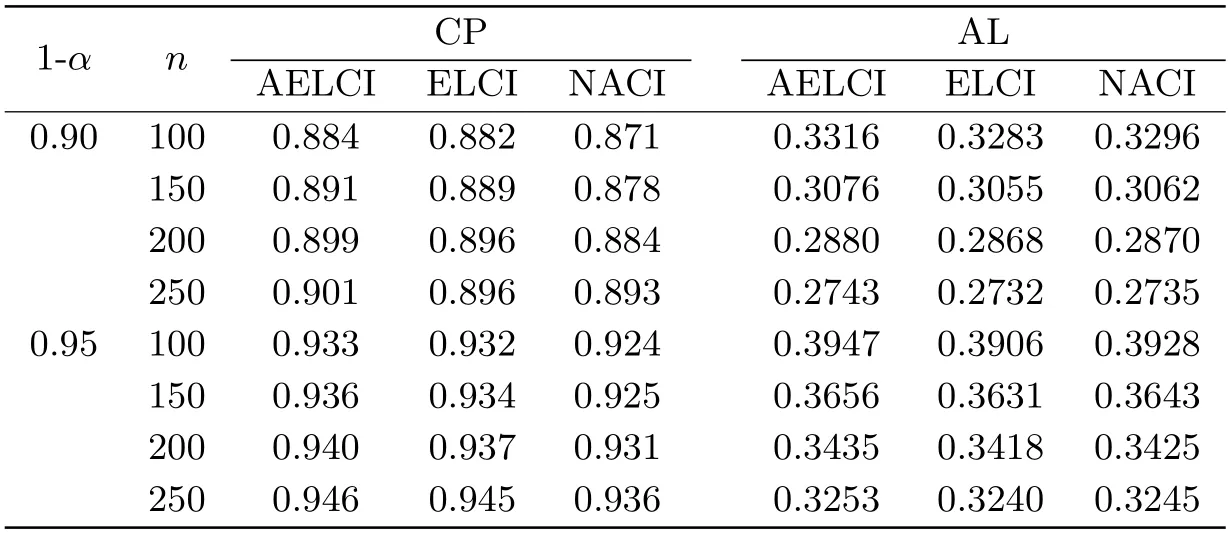
表1 多元正態分布隨機樣本下置信度為0.90和0.95時f(1)的置信區間的CP和AL

由表1得,在多元正態隨機樣本下,隨著樣本量的不斷增大,置信區間的覆蓋率逐漸增大且越來越接近于置信度,置信區間的平均長度逐漸減小.當n相同時,AEL方法的置信區間的覆蓋率高于EL和NA兩種方法的置信區間的覆蓋率,雖然AEL方法置信區間的平均長度略大于EL和NA兩種方法的置信區間的平均長度,但是相差非常小.因此綜合分析可得,多元正態隨機樣本下,AEL的表現略優于EL和NA的表現.

ii) 多元t分布隨機樣本

在本節模擬中,(X1,···,Xn)是多元t分布隨機向量,且滿足E(X1,···,Xn)=(1,···,1),Cov(Xi,Xj)=-3-(j-i)-1(1≤i ≤n,j>i) 和Var(Xi)=5/3(1≤i ≤n),取an=0.5,由此生成的{Xi;1≤i ≤n}是負相協序列(見文[17]),該情形下的模擬結果見表2.

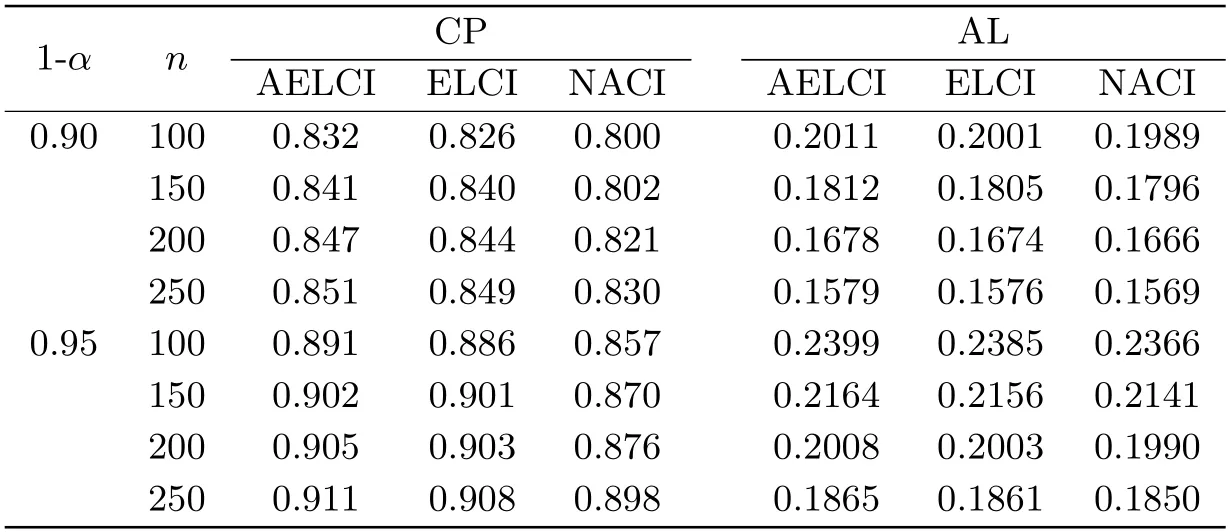
表2 多元t分布隨機樣本下置信度為0.90和0.95時f(1)的置信區間的CP和AL

由表2得,在多元t分布隨機樣本下,隨著樣本量的不斷增大,三種方法的置信區間的覆蓋率均逐漸增大且越來越接近置信度,置信區間的平均長度均不斷減小.當n相同時,AEL方法的置信區間的覆蓋率高于EL和NA兩種方法的置信區間的覆蓋率,盡管其置信區間的平均長度也稍有增加,但與EL和NA的置信區間的平均長度相比相差甚微.綜合分析可得在多元t分布隨機樣本下,AEL表現略好于EL和NA的表現.

因此一般來說,在正相協隨機樣本下,AEL表現略好于EL和NA的表現.此外,通過對比兩種不同分布隨機樣本下的模擬結果可得,當n取同一值時,多元正態分布樣本下三種方法的置信區間的覆蓋率都更高且更接近于置信度,因此可得三種方法在多元正態分布隨機樣本下的表現均優于在多元t分布隨機樣本下的表現.

Ⅱ 正相協樣本

由表3、表4得,從置信區間覆蓋率來看,隨著樣本量的不斷增大,兩種隨機分布樣本下置信區間的覆蓋率均不斷增加且越來越接近置信度,當n相同時,AEL的置信區間的覆蓋率高于EL和NA的置信區間的覆蓋率.從置信區間的平均長度來看,兩種隨機分布樣本下置信區間的平均長度均隨著樣本量的增加不斷減小.盡管AEL方法在置信區間的覆蓋率增大的同時其平均長度也稍有增加,但其與EL和NA的置信區間的平均長度相比相差甚微.

表3 ～N(1,1)情形下置信度為0.90和0.95時f(1)的置信區間的CP和AL

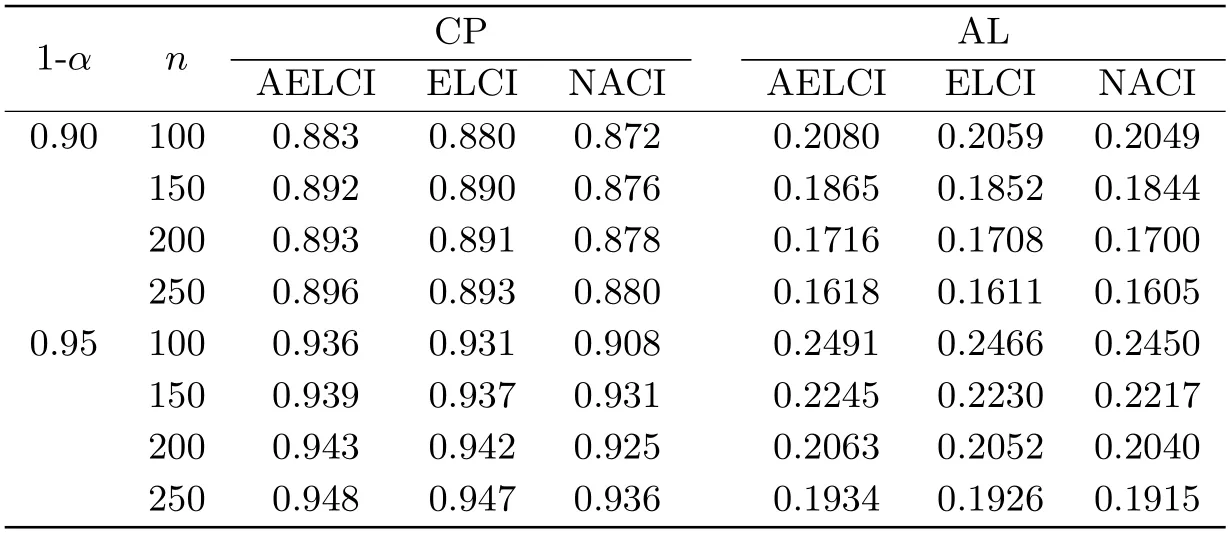
表3 ～N(1,1)情形下置信度為0.90和0.95時f(1)的置信區間的CP和AL

表4 ～情形下置信度為0.90和0.95時f(1)的置信區間的CP和AL

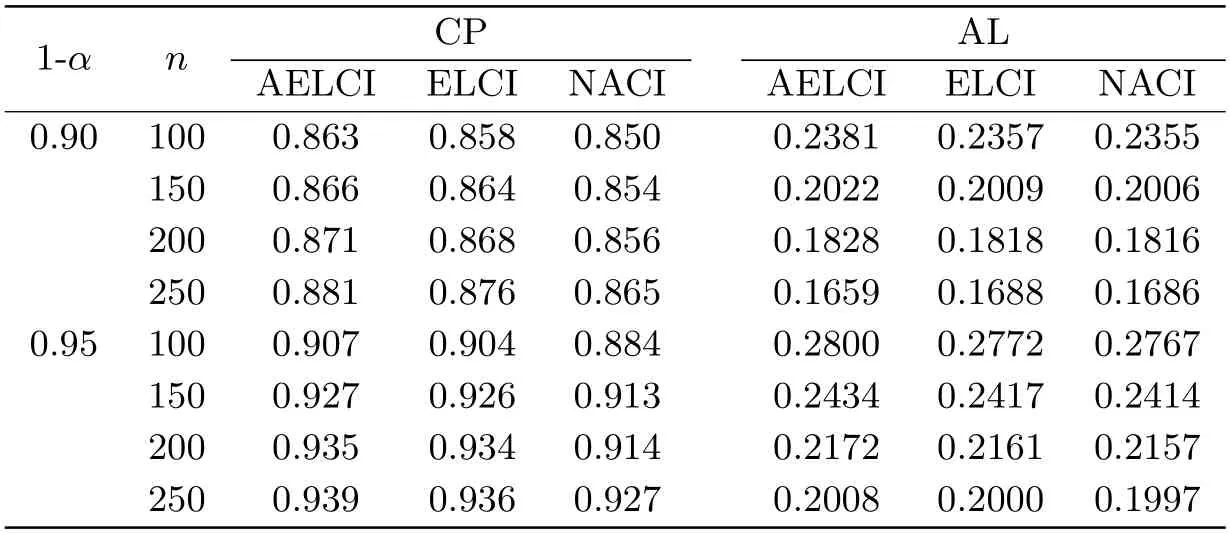
表4 ～情形下置信度為0.90和0.95時f(1)的置信區間的CP和AL

綜合分析可得,正相協樣本下,AEL的表現略好于EL和NA.此外,通過兩表對比可得,當n取相同值時,正態分布樣本下三種方法對的置信區間的覆蓋率更高且更接近于置信度,且置信區間的平均長度也更短,由此可得三種方法在正態分布隨機樣本下的表現優于在卡方分布隨機樣本下的表現.

綜上可得,相協樣本下(正相協或負相協),對于概率密度函數置信區間的估計,AEL方法的表現略好于EL和NA兩種方法的表現,且三種方法均在正態分布隨機樣本下表現得更好.

此外,通過模擬結果發現,在相協樣本下文中提到的三種方法得到的置信區間的覆蓋率一致低于名義覆蓋水平1-α,嘗試增大樣本量進行模擬發現(模擬結果不再列出),置信區間的覆蓋率有所改善且偶爾出現高于置信度1-α的情形,但是與樣本量較小時模擬結果相比,樣本量增大時AEL方法的表現優于EL和NA的表現的程度有所下降.因此,AEL方法更適合在樣本量較小時使用,在樣本容量較大時,EL和AEL的表現相差不大.在獨立樣本情形下,Tsao[18]討論了EL置信區間的覆蓋率常常低于名義覆蓋水平的情況,并且從理論上分析了出現這一現象的原因,相協樣本情況下EL置信區間出現低覆蓋的原因尚需進一步研究.

4.引理

以下引理將用于后面定理的證明,其中引理4.1-4.3的證明見文[15]的引理4.1-4.3的證明.

引理4.11)設條件(A1)(i)-(iv),(A2)(i)(ii),(A3)(i)-(iii)成立,則對于f的連續點x有

2)設條件(A1)-(A3)成立,則

引理4.2設條件(A1)(i)(v)和(A2)(i)成立.則對于任意的l ∈n有

引理4.3設條件(A1)-(A3)成立,則

引理4.4設條件(A1)-(A3)成立,則

5.定理證明

定理2.1的證明1) 首先證明

利用最大化問題的對偶性可得

因為M可任意大,則對于θf(x),當n →∞時,依概率趨于1有-2(nh)-1/3W?(θ)→∞成立.對于-2(nh)-1/3W(θ)→∞的證明與-2(nh)-1/3W?(θ)→∞的證明相似.

定理2.2證畢.