基于EKF 的GMAW 實時焊縫跟蹤研究*

楊園洲 薛瑞雷 劉宏勝 夏 磊

（新疆大學智能制造現代產業學院（機械工程學院），新疆 烏魯木齊 830017）

GMAW 是碳鋼、不銹鋼的主流焊接工藝，采用GMAW 自動焊可顯著提高生產效率（4～5 倍）[1]。在弧焊過程中，工件與導電嘴間距離（contact-tipto-work distance，CTWD）會使弧長發生變化，通過控制焊接電流可以控制CTWD，讓弧長保持穩定，但是由于工件受到自身加工誤差、熱變形等因素的影響，焊槍無法保持恒定的高度，影響焊接質量[2-3]。

自動焊接的前提是焊縫跟蹤，通過聲、電和視覺傳感器檢測焊縫是實現焊縫跟蹤的常用方法[4]。聲音傳感器實時性高，但易受噪聲影響，精度較低。視覺傳感器精度高，可提前檢測焊縫位置，但實時性弱，易受干擾，易引入超前誤差。電弧傳感器通過下位機進行判斷，運算速度快，不受弧光、飛濺和煙塵等于擾，可直接獲取焊槍的位置，結構簡單，成本低[5]。所以本文選擇電弧傳感器來實現焊縫跟蹤。高延峰等[6]采用比例和參數自調整模糊控制實現焊縫跟蹤。洪波等[7]分析磁控電弧信號的頻譜，提出了一種基于滑動固定數據窗的電弧信號實時小波降噪方法。張鋒等[8]設計了FIR 和一種模糊控制器進行偏差調整。Fabry C 等[9]使用電弧傳感和光學測量來控制每個焊道的擺動角幅度、送絲速度和焊接速度的變化。Lei T 等[10]針對環形焊縫多且密集的管板焊接提出了一種基于直流脈沖方波的電弧電壓實時跟蹤算法與二維和三段模糊控制器。國內外目前在焊縫跟蹤方面的研究主要采用模糊控制來實現焊縫的控制，但是精度和運行穩定性還不夠。

焊接過程中往往呈現出非線性特性，并且焊接環境中存在的噪聲和干擾可能影響焊縫跟蹤系統的性能，導致跟蹤不穩定。本文通過數學模型法檢測焊槍的高度偏差和水平偏差，并通過EKF 算法對焊接偏差進行狀態估計，以此完成GMAW 自動化焊接過程中對焊槍的實時精準調節。

1 實驗平臺

本文是針對圖1 所示的坡口進行實驗，試驗材料為Q235 低碳鋼，工件尺寸為長300 mm、寬150 mm、高25.7 mm，填充材料為實心碳鋼焊絲，直徑為1.2 mm。圖2 所示為焊縫跟蹤系統的結構圖，由GMAW 焊接設備、信息采集設備和控制設備組成。GMAW 焊接設備包括管道焊接工作站、ASM-500 數字化多功能焊機、保值久WRA-300s 焊機循環冷卻水箱、送絲機。信息采集設備由J-LK-KT 系列霍爾電流傳感器和數據采集卡組成，實現電流信號的采集與存儲。控制設備由控制機構和計算機組成，實現啟停工作站的引弧以及控制焊槍。焊槍運動軌跡如圖3 所示。

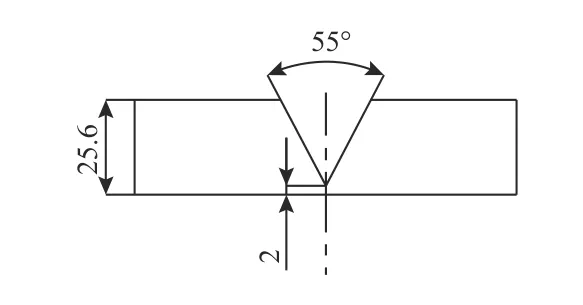
圖1 焊縫坡口

圖2 焊縫跟蹤系統結構示意圖

圖3 焊槍運動軌跡

2 信息采集與處理

2.1 信號預處理

FIR 可以有效濾除高頻噪聲和干擾，從而減少噪聲對焊接信號的干擾，有助于提取焊接質量相關的信號信息。焊接過程中的關鍵信息通常包含在低頻部分，FIR 有助于保留這些低頻信號，以進行焊接過程的監測和控制。FIR 主要特點是沒有反饋，僅依賴于輸入信號的當前和過去的樣本，這使得FIR 非常穩定。在FIR 中，較低的階數可以減少計算量，而較高的階數可以獲得更好的濾波特性，但計算量會相應增加。

FIR 的輸出信號可以通過式（1）計算：

式中：y[n]為輸出信號的當前樣本，x[n-k]為輸入信號的當前樣本，h[k]為FIR 的第k個系數，N為FIR 的階數。

圖4 所示為采樣頻率為100 ms，試件向左偏移3 mm 時的原始數據與濾波后的數據對比情況。濾波前，電流波形變化夾雜著隨機噪聲和尖峰信號；濾波后，電流波形逐步平緩，且隨機噪聲和尖峰信號逐漸被濾除。波形可反映出電流的變化趨勢。

圖4 原始數據與濾波后的數據對比圖

2.2 焊槍高度檢測

高度跟蹤是焊接過程中將電流通過FIR 濾波器處理后，利用焊槍高度與電流的數學模型計算出高度偏差，通過EKF 實現焊縫高度跟蹤，如圖5 所示。

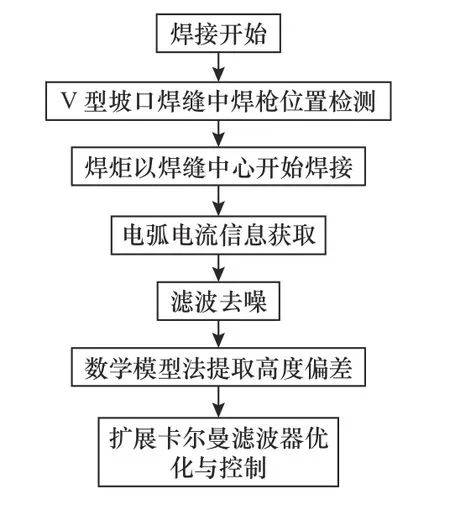
圖5 焊縫高度跟蹤流程圖

焊接過程存在靜態特性和動態特性。靜態特性指焊接過程中參數不隨時間變化。動態特性指焊接過程中的瞬時變化和波動性質。靜態特性分析可以用于確定焊接參數的最佳值，以獲得最佳的焊接質量；動態特性分析可以用于監測焊接過程，用來發現不良焊縫并采取措施加以糾正。所以本文是針對焊接的動態特性展開的研究，為后續的研究提供貢獻。

由于電流隨CTWD 的變化而變化，在給定焊接速度和送絲速度的條件下，焊接平均電流和CTWD成正比例關系，其關系可寫成式（2）：

式中：H為一個擺動周期內焊槍的高度；I為焊接平均電流；K、b 均為常數。

為了獲取K、b 的值，通過采集CTWD 從15 mm變化到20 mm 的電流，將電流分成不同的區間段來求取均值，并通過最小二乘法擬合出H與I的關系，如圖6 所示。

圖6 高度跟蹤數學模型圖

為了避免剛開始時的電弧的穩定狀態對焊縫跟蹤過程造成偏差，通常會排除焊接開始的2～3 s 內的電流信號值。擬合出的公式如下：

數學模型通過焊槍驟降到3 mm 來驗證，焊接電流如圖7 所示，焊縫如圖8 所示。

圖7 高度跟蹤數學模型驗證實驗電流變化圖

圖8 CTWD 從15 mm 驟降到12 mm 的焊縫

2.3 焊槍水平偏差提取

水平跟蹤是先對電弧傳感器提取的電流信息濾波處理，后獲取在同一個周期內左右半周期的電流值的積分差，通過EKF 將焊縫偏差電流數值轉化為焊槍偏移數據，如圖9 所示。

圖9 焊縫水平跟蹤流程圖

從2.2 節高度跟蹤的數學模型的研究可知，CTWD 和焊接電流呈線性關系，這是焊縫水平跟蹤的理論基礎。對于水平偏差提取的算法有多種，如：極限位置電流差值法，此算法簡單，但受電弧穩定性影響大；特征諧波檢測法可以直接反映焊縫的橫向偏差，但對傳感器要求較高，且計算復雜；直接測位法計算直觀，但需大量比較，精度較低；積分差值法能反映焊縫位置，不受電弧穩定性影響。

本文使用積分差值法計算焊槍偏差，如圖10所示，其中焊槍連續兩次到達中心位置過程中電流的積分值作為一側的特征參數，通過式（4）和式（5）計算左右兩側的積分差值，并獲取在同一個周期內左右半周期的電流值的積分差，通過式（6）得到水平位置偏差。

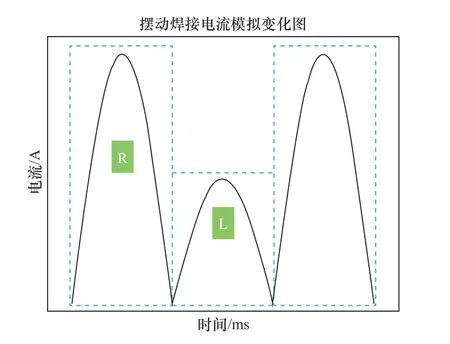
圖10 積分差值法偏差計算方法

式中：I0、I1分別為焊槍在同一周期內左、右半周期的平均電流值；N為每個擺動周期的采樣點數；h為積分步長，h=2π/N。

式中：E為焊槍水平偏差；K為電流積分差和偏差的相關系數，利用最小二乘法擬合后K為0.570 7。

2.4 焊縫跟蹤控制算法——EKF

由于焊接系統為非線性時變系統，焊接系統通常涉及焊接溫度、電流、電壓和速度等。這些變量之間相互作用，使得對整個系統進行建模和控制變得更加復雜。而EKF 是在卡爾曼濾波的基礎上，通過線性化非線性系統模型和非線性觀測模型來處理非線性的系統和觀測方程。對于焊接過程中的非線性系統控制問題，可以使用EKF 來跟蹤和估計焊接過程中的狀態變量，而且EKF 通常更簡單且計算效率較高。此外，焊縫跟蹤中傳感器通常無法獲取全面的信息，獲取的信息也常常夾雜著噪聲。EKF 可以通過對測量數據進行加權處理，并根據測量數據和先驗知識共同更新參數和狀態的估計，從而提供準確的數據，以此提高焊接質量，提升焊縫跟蹤的精度。

EKF 使用泰勒級數展開來將非線性狀態轉移方程和非線性觀測方程在當前狀態估計值附近進行線性化，后對線性化方程進行預測和校正。在EKF的應用中，核心是在EKF 框架下確定系統的狀態轉移模型和觀測模型。算法的步驟如圖11 所示。

圖11 擴展卡爾曼濾波器算法的運算過程

2.4.1 初始化

2.4.2 時間更新（預測）

（1）利用系統模型對當前狀態進行預測，見式（7）和式（8）。根據焊接時的狀態空間方程式（9）和測量方程式（10），并通過使用前一時刻的狀態估計值和控制輸入u[k-1]來預測當前時刻的狀態值。

式中：f()為非線性動態方程和非線性測量方程，u[k-1]為輸入向量；z[k]=h()為測量方程；過程噪聲w～N(0,Qc)，服從正態分布，期望為0，狀態協方差矩陣為Qc；測量噪聲v～N(0,Rc)，服從正態分布，期望為0，狀態協方差矩陣為Rc

（2）利用雅可比矩陣（Jacobian Matrix）線性化系統模型，見式（11）和式（12）。由于系統模型是非線性的，需要通過在當前狀態點處對系統模型進行一階泰勒展開來進行線性化。

2.4.3 測量更新（校正）

（1）利用雅可比矩陣線性化測量模型，見式（13）和式（14）。由于測量模型也是非線性的，需要通過求解雅可比矩陣來近似非線性測量模型。

（2）計算卡爾曼增益K[k]。通過將預測誤差協方差矩陣與測量誤差協方差矩陣進行加權和的逆矩陣相乘，得到K[k]，用于校正預測誤差，見式（15）。

2.4.4 重復執行步驟2 和步驟3

直到所有測量值被處理完畢或達到預設的停止條件。在每個步驟中，每次迭代的先驗狀態估計是由上一次的后驗狀態估計通過系統模型進行預測得到的。通過預測和校正的不斷迭代，以獲得更準確的狀態估計。

這些步驟構成了EKF 算法的基本框架，并用于在非線性系統和非線性觀測模型的情況下進行狀態估計。通過迭代預測和校正步驟，EKF 能夠逐步優化對系統狀態的估計，并考慮預測誤差和測量誤差，以獲得最準確的狀態估計。本文在焊縫跟蹤過程中，建立了焊縫位置參數的狀態方程和測量方程，并對系統狀態進行預測和估計，從而獲得準確的焊槍相對焊縫中心的位置，提高了焊縫跟蹤的精度。

3 實驗驗證

3.1 跟蹤驗證方案

實驗方案見表1，焊接位置為平焊區，本文設計了高度、水平和整體跟蹤實驗來驗證算法的穩定性和可行性。高度跟蹤試驗如圖12 所示，通過抬高試件來模型管道焊接時的垂直方向的誤差。水平跟蹤試驗如圖13 所示，通過偏移試件來模型管道焊接時的水平方向的誤差，水平方向焊槍行走軌跡如圖14 所示。高度跟蹤實驗中，抬高試件一側4 mm；水平模型驗證實驗中，偏移試件一側5 mm；整體跟蹤模型驗證實驗中，抬高試件一側4 mm，同時偏移試件同一側5 mm。以上選擇的誤差均符合焊接工藝中所描述的管道組對坡口偏差不超過管道厚度20%的標準，因為板厚為25.6 mm，則誤差為5 mm 以內。焊接時的焊接參數見表2，本文采用固定焊接參數的方式來進行實驗，因為焊接參數對焊縫跟蹤的影響較大。當焊接參數變化時，焊縫熱量也會變化，焊縫邊緣容易出現熔池擴大、噴濺等現象，容易出現不良焊縫形狀，會影響焊縫跟蹤，影響實驗的有效性。

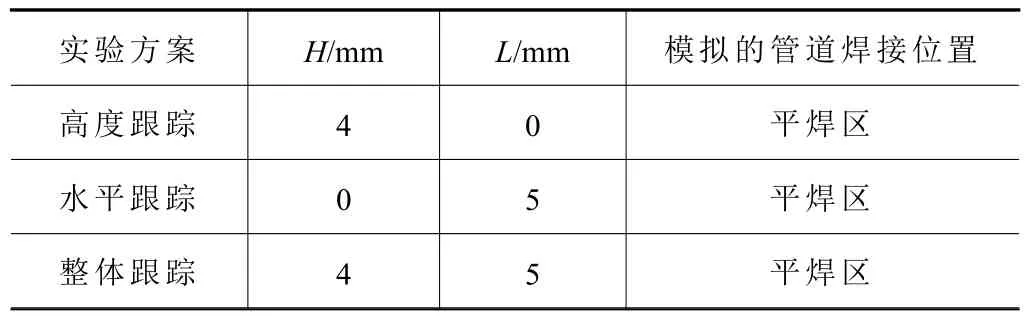
表1 試驗方案

表2 焊接參數

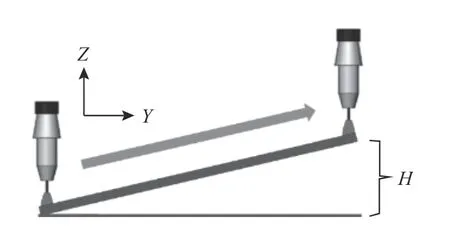
圖12 垂直方向偏離焊縫實驗

圖13 水平方向偏離焊縫實驗

圖14 實際焊接工件狀態

3.2 實驗結論

高度跟蹤實驗中，利用數學模型實現焊槍高度偏差的采集和處理，并利用EKF 實現垂直方向的糾偏。高度跟蹤軌跡曲線如圖15 所示，焊槍初始高度為15 mm，高度偏差維持在±0.25 mm 以內，焊縫成形圖如圖16 所示。

圖15 高度跟蹤軌跡曲線（H=4 mm）

圖16 試件一側抬高4 mm 焊縫圖

水平模型驗證實驗中，利用水平跟蹤模型實現焊槍水平偏差的采集和處理，然后利用EKF 實現水平方向的糾偏控制，水平跟蹤軌跡曲線如圖17所示，水平偏差維持在±0.25 mm 以內，焊縫成形圖如圖18 所示。

圖17 水平跟蹤軌跡曲線（L=5 mm）

圖18 試件一側偏移5 mm 焊縫圖

整體跟蹤模型驗證實驗中，抬高試件一側4 mm，偏移試件同一側5 mm，之后利用整體跟蹤模型實現焊槍高度和水平偏差的采集和處理，然后利用EKF 實現垂直和水平方向的糾偏控制，高度和水平跟蹤軌跡曲線如圖19 所示，焊槍初始高度為15 mm，高度偏差和水平偏差維持在±0.25 mm 以內。

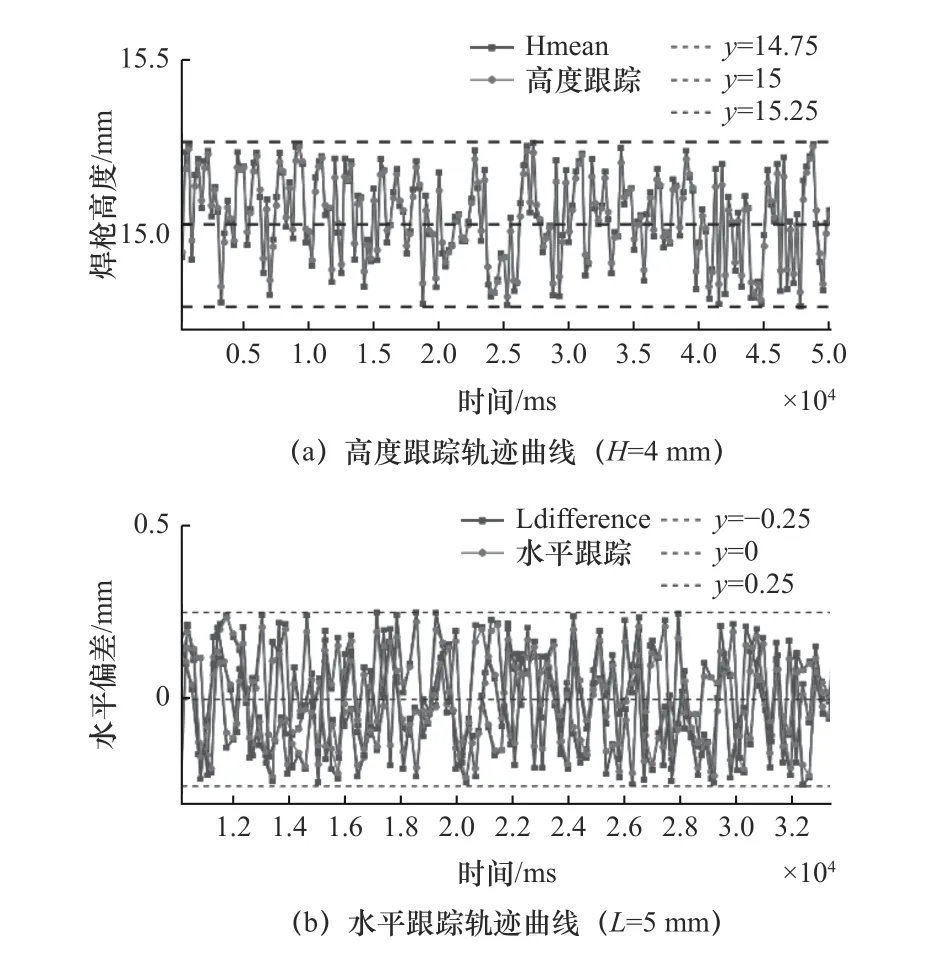
圖19 整體跟蹤軌跡曲線

通過以上三組實驗可得出以下結論：計算得到的偏差符合偏差維持在0.5 mm 以內這一跟蹤指標（圖20），跟蹤的精度均符合焊接工藝中所描述的自動焊接誤差≤0.5 mm 這一精度要求[11]，并且焊縫成形良好，無明顯凸起，能夠滿足實際焊接要求，說明焊槍的整體跟蹤算法可行。

圖20 試件一側抬高4mm 和偏移5mm 焊縫圖

4 結語

基于EKF 的GMAW 實時焊縫跟蹤技術主要由GMAW 焊接設備、信息采集設備和控制設備組成。實驗結果表明，該技術用于焊接設備對焊槍的跟蹤是可行和穩定的。本研究的主要成果可概括如下：

（1）針對V 形坡口焊縫的焊接電流的特點，建立了高度和水平偏差提取數學模型，解決了焊槍擺動中心對準焊縫中心的問題。

（2）采用了EKF 算法解決了焊接過程中的非線性、噪聲和干擾等問題，實現對焊槍的精確控制。

（3）焊槍焊縫實時跟蹤的偏差成功控制在0.5 mm以內，滿足了焊接質量和焊縫跟蹤控制的要求。

為GMAW 實時焊縫跟蹤技術的發展提供了重要依據。