一類(lèi)考慮雙隔離強(qiáng)度的傳染病模型的穩(wěn)定性研究
宋家城, 呂王勇,2*, 張 萍, 張 策, 史思紅
(1. 四川師范大學(xué) 數(shù)學(xué)科學(xué)學(xué)院, 四川 成都 610066; 2. 四川師范大學(xué) 可視化計(jì)算與虛擬現(xiàn)實(shí)四川省重點(diǎn)實(shí)驗(yàn)室, 四川 成都 610066; 3. 海南師范大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院, 海南 海口 570311)
眾所周知,傳染病比如鼠疫、霍亂、傳染性非典型肺炎、艾滋病、病毒性肝炎等,不僅影響著人們的身心健康,而且還對(duì)經(jīng)濟(jì)的發(fā)展產(chǎn)生了一定的影響,更嚴(yán)重的甚至對(duì)人們的出行產(chǎn)生了影響,并且每年死于傳染病的人不計(jì)其數(shù).因此,很多學(xué)者針對(duì)傳染病建立了一系列模型,并進(jìn)行了相關(guān)的研究,例如:吳長(zhǎng)青等[1]在總?cè)丝诜浅?shù)條件下,研究了一類(lèi)SIRS傳染病模型的所有非負(fù)平衡點(diǎn),以及平衡點(diǎn)的存在性、局部穩(wěn)定性.高宏偉等[2]則考慮了一類(lèi)具有非線(xiàn)性傳染率、隔離率的SIRS傳染病模型解的存在性.李明山等[3]考慮了一類(lèi)連續(xù)SIR傳染病模型的分岔性質(zhì).由于隔離措施和治療措施對(duì)傳染病的防控起到很重要的作用.因此,閆慧林等[4]考慮了一類(lèi)具有隔離和治療措施的新型冠狀病毒肺炎(COVID-19)傳染病模型.朱翌民等[5]考慮了隔離措施對(duì)COVID-19疫情控制的影響.豐利香等[6]考慮了具有隔離和不完全治療的傳染病模型.對(duì)于傳染病的研究一直在不斷進(jìn)行[7-16],這為傳染病的預(yù)防和控制提供了一定程度的支持.
傳染病無(wú)時(shí)無(wú)刻不在人們的身邊,我國(guó)一直對(duì)感染者實(shí)行隔離措施,以此來(lái)減少對(duì)易感者的感染,并且一些易感人群會(huì)由于媒體報(bào)道等原因,自覺(jué)做好防護(hù)措施從而變成有意識(shí)的易感者.同時(shí)考慮到感染者有顯性和隱性之分,其中顯性感染者指的是感染各種病原體之后,患者已經(jīng)有相關(guān)的臨床癥狀了,而隱性感染者指的是感染了各種病原體之后,沒(méi)有表現(xiàn)出相應(yīng)的臨床癥狀.由于上述文章并沒(méi)有對(duì)顯性感染者和隱性感染者都建立隔離倉(cāng),因此本文對(duì)顯性感染者和隱性感染者都建立隔離倉(cāng),并認(rèn)為不僅顯性感染者可以變?yōu)殡[性感染者,而且被隔離的隱性感染者也可以變成被隔離的顯性感染者,同時(shí)把易感者分成無(wú)意識(shí)易感者和有意識(shí)易感者,由此引入了有意識(shí)易感者接觸感染者的調(diào)節(jié)因子,并且考慮到傳染病一般都存在潛伏期,潛伏期患者也具有傳染的風(fēng)險(xiǎn),最后考慮到隱性感染者和顯性感染者都有自愈的可能性,基于此建立了帶有雙隔離強(qiáng)度的傳染病模型,并分析雙隔離強(qiáng)度對(duì)傳染病的影響.
1 模型建立
本文建立了一類(lèi)具有雙隔離強(qiáng)度的傳染病模型,該模型中共有8個(gè)倉(cāng)室:無(wú)意識(shí)易感者(S1)、有意識(shí)易感者(S2)、潛伏者(E)、顯性感染者(I)、隱性感染者(A)、被隔離的顯性感染者(Q)、被隔離的隱性感染者(M)、恢復(fù)者(R).本文考慮把易感者分成無(wú)意識(shí)易感者(S1)和有意識(shí)易感者(S2),認(rèn)為無(wú)意識(shí)易感者(S1)由于媒體報(bào)道等原因會(huì)變成有意識(shí)易感者(S2).又考慮到一般傳染病都存在潛伏期,故建立了一個(gè)潛伏者(E)的倉(cāng)室,并且認(rèn)為不僅隱性感染者和顯性感染者會(huì)感染易感者,潛伏期的人群也會(huì)感染易感者,用βE表示無(wú)意識(shí)易感者與潛伏者接觸的傳染率,βA表示無(wú)意識(shí)易感者與隱性感染者接觸的傳染率,βI表示無(wú)意識(shí)易感者和顯性感染者接觸的傳染率,為了區(qū)分有意識(shí)易感者和無(wú)意識(shí)易感者接觸感染者的幾率不同,引入了有意識(shí)易感者接觸感染者的調(diào)節(jié)因子σ.同時(shí)也把隱性感染者(A)和顯性感染者(I)都建立了隔離倉(cāng),分別用被隔離的隱性感染者(M)和被隔離的顯性感染者(Q)表示,同時(shí)認(rèn)為隱性感染者(A)可以變成顯性感染者(I),并且被隔離的隱性感染者(M)經(jīng)過(guò)一段時(shí)間后也會(huì)變成被隔離的顯性感染者(Q).又考慮到隱性感染者(A)和顯性感染者(I)被隔離的概率也是不一樣的,q表示顯性感染者的隔離率,即被追朔到為顯性感染者的概率,ξ表示隱性感染者的隔離率,即被追朔到為隱性感染者的概率,最后考慮到隱性感染者(A)和顯性感染者(I)都有自愈的可能性,即隱性感染者有一定的概率η變?yōu)榛謴?fù)者(R),顯性感染者也有一定的概率α變成恢復(fù)者(R).基于上述說(shuō)明建立了S1S2EIAQMR模型.模型的參數(shù)定義見(jiàn)表1,模型的傳播機(jī)制見(jiàn)圖1.
根據(jù)模型傳播流程圖建立如下的模型:
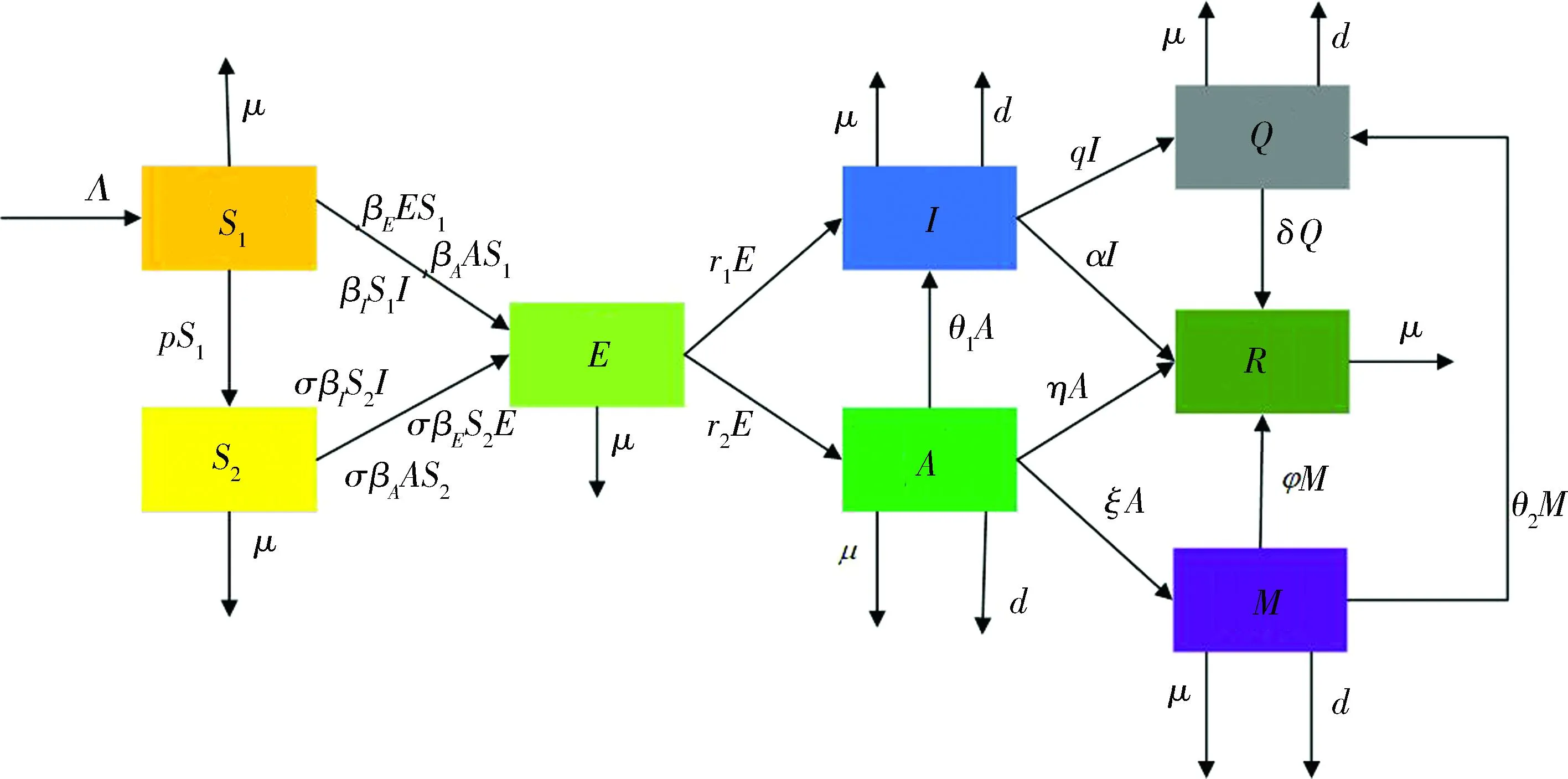
圖 1 S1S2EIAQMR模型的傳播流程圖

表 1 S1S2EIAQMR模型的參數(shù)定義
由(1)式知:參變量R可以其他7個(gè)參變量S1、S2、E、I、A、Q、M表示出來(lái),而且參變量R在系統(tǒng)前7個(gè)方程中并未出現(xiàn),因此只需要考慮系統(tǒng)(1)的子系統(tǒng)(2):
2 正性和不變集
對(duì)于系統(tǒng)(2),可以得到
Λ-μ(S1+S2+E+I+A+Q+M)-
d(I+A+Q+M)-αI-ηA-φM-δQ≤
Λ-μ(S1+S2+E+I+A+Q+M).
因此
S1(t)+S2(t)+E(t)+I(t)+
又因?yàn)槟P椭锌紤]的是人類(lèi),所以
S1(t)+S2(t)+E(t)+I(t)+
A(t)+Q(t)+M(t)>0.
綜上可得
將在不變集Ω上討論系統(tǒng)的穩(wěn)定性.
3 平衡點(diǎn)分析
為了對(duì)平衡點(diǎn)進(jìn)行分析,首先計(jì)算出無(wú)病平衡點(diǎn),基本再生數(shù)和地方病平衡點(diǎn),并證明了地方病平衡點(diǎn)的唯一性,最后對(duì)無(wú)病平衡點(diǎn)和地方病平衡點(diǎn)進(jìn)行了穩(wěn)定性分析.
3.1 無(wú)病平衡點(diǎn)與基本再生數(shù)令系統(tǒng)(2)的右側(cè)等于0,并且令E=I=A=Q=M=0,則可以得到:
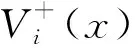
(βEES1+βAAS1+βIIS1+
σβAAS2+σβEES2+σβIIS2,0,0,0,0,0)T,
其中
G=βEFC+βIFD+βAr2C,F=μ+d+θ1+η+ξ,
C=μ+d+q+α.
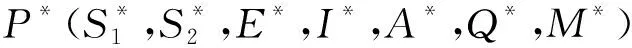
由方程(3)的第1個(gè)式子,可得
(4)
將(4)式代入方程(3)的第2式,可得
S2=
則
同時(shí),由方程(3)的第4和5式可得
r1E+θ1A=(μ+d+α+q)I.
整理可得
于是上式可寫(xiě)為
(5)
將(5)式代入方程(3)的第3式,可得
于是
又令
C1=CF,D1=DF.
于是可得
(6)
直接對(duì)I求導(dǎo)得
其中
D2=σD1G[GI+(p+μ)D1][σGI+μD1]-
D1G[σGI+(pσ+μ)D1]{σGI+μD1+
σ[GI+(p+μ)D1]}=
D1G{σ[GI+(p+μ)D1][σGI+μD1]-
[σGI+(pσ+μ)D1][σGI+μD1+
σ[GI+(p+μ)D1]]}=
D1G{[σGI+σ(p+μ)D1-σGI-(pσ+
μ)D1][σGI+μD1]-
σ[GI+(p+μ)D1][σGI+(pσ+μ)D1]}=
D1G{(σμD1-μD1)(σGI+μD1)-
[σGI+(pσ+μ)D1]σ[GI+(p+μ)D1]}=
σ2G2I2-(pσ+μ)D1σGI-
-D1G{μD1(σμD1+μD1)+
σ[σG2I2+σpD1GI+G(pσ+μ)D1I+
-D1G{(σG)2I2+2σD1G(pσ+μ)I+
故K′(I)<0.所以K(I)是關(guān)于I的單調(diào)遞減函數(shù),又因?yàn)?/p>
且
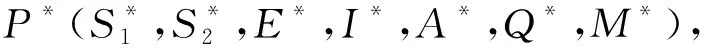
其中I*是方程K(I)=0的唯一正根.
3.3 無(wú)病平衡點(diǎn)的局部穩(wěn)定性
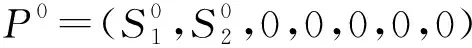
證明系統(tǒng)在P0處的雅可比矩陣為
其中
D3=μ+d+φ+θ2,
接下來(lái)求雅可比矩陣J(P0)的特征值:
|λE-J(P0)|=0=
化簡(jiǎn)可得
|λE-J(P0)|=
(λ+μ+p)(λ+μ)(λ+μ+d+δ)(λ+D3)×
顯然-(μ+p)、-μ、-(μ+d+δ)、-D3為J(P0)的特征值,矩陣的另外3個(gè)特征值滿(mǎn)足方程
展開(kāi)可得
λ3+D7λ2+D8λ+D9=0,其中
D7=(μ+r1+r2)(1-R0)+
D8=(1-R0)(μ+r1+r2)(C+F)+
D9=(1-R0)(μ+r1+r2)CF+D5r2θ1,D7D8-D9=D7(D8-CF)+
(C+F)CF+D5Fr1+D6Cr2.
當(dāng)R0<1時(shí),D7,D8,D9>0.并且當(dāng)R0<1時(shí)有
Δ1=D7>0,
于是由Routh-Hurwitz判別法可以得到:雅可比矩陣J(P0)的所有特征值都是負(fù)數(shù),故無(wú)病平衡點(diǎn)是局部漸近穩(wěn)定的.證畢.
3.4 無(wú)病平衡點(diǎn)的全局穩(wěn)定性
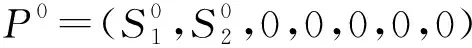
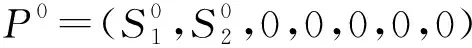
則系統(tǒng)(2)可以被改寫(xiě)為
定義Lyapunov函數(shù)
則L1沿系統(tǒng)的全導(dǎo)數(shù)為:
現(xiàn)令
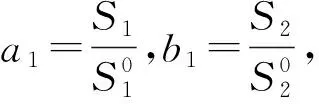
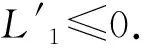
3.5 地方病平衡點(diǎn)的全局穩(wěn)定性
定理 4對(duì)于系統(tǒng)(2),當(dāng)R0>1時(shí),地方病平衡點(diǎn)P*是全局漸近穩(wěn)定的.
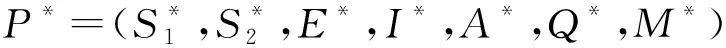
作如下變換,并記
則系統(tǒng)(2)可以被改寫(xiě)為
其中
并定義Lyapunov函數(shù):
K1I*(z-1-lnz)+K2A*(h-1-ln h)+
K3Q*(l-1-lnl)+K4M*(n-1-ln n),則L4沿系統(tǒng)的全導(dǎo)數(shù)為
通過(guò)化簡(jiǎn),可得
K2r2E*+K3qI*+K3θ2M*+K4ξA*-
K1r1E*-K1θ1A*+K3qI*)+
K1θ1A*-K2r2E*+K4ξA*)+
l(-K3qI*-K3θ2M*)+n(K3θ2M*-K4ξA*)-
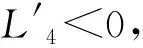
從上式可得
K3=0,K4=0.
于是L4沿系統(tǒng)的全導(dǎo)數(shù)為
根據(jù)均差不等式的性質(zhì),利用一種代數(shù)方法[8]定義函數(shù)L5如下:
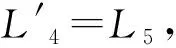
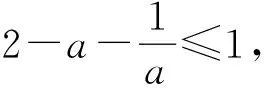
4 基本再生數(shù)的敏感性分析
由基本再生數(shù)R0的表達(dá)式,利用基本再生數(shù)進(jìn)行參數(shù)的敏感性分析[9],以顯性感染者的隔離率q為例,結(jié)果如下:
q[(βEF+βAr2)C-G]×
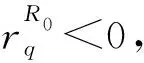
5 結(jié)論
本文建立了一類(lèi)具有雙隔離強(qiáng)度的傳染病模型,首先確定了系統(tǒng)的正性和不變集,其次分析了模型的無(wú)病平衡點(diǎn)和基本再生數(shù)R0,然后計(jì)算了地方病平衡點(diǎn)并證明了地方病平衡點(diǎn)的唯一性.之后證明了平衡點(diǎn)的穩(wěn)定性,即當(dāng)R0<1時(shí),無(wú)病平衡點(diǎn)不僅是局部漸近穩(wěn)定的,也是全局漸近穩(wěn)定的,即疾病最終消除;當(dāng)R0>1時(shí),通過(guò)構(gòu)造Lyapunov函數(shù)來(lái)說(shuō)明,地方病平衡點(diǎn)是全局漸近穩(wěn)定的,即疾病將持續(xù)存在.然后通過(guò)對(duì)基本再生數(shù)的敏感性分析,得到增加隱性感染者和顯性感染者隔離強(qiáng)度都可以減小基本再生數(shù),從而可以控制疾病的蔓延.

